授人以鱼 不如授人以渔

摘 要：培养和提升学生的数学探究能力是数学教学的重要目标，本文从创设情境、拓展时空、体验过程、设计练习四个方面来谈谈如何培养学生的数学探究能力。

关键词：数学;探究;能力

古人云：“授人以鱼，不如授人以渔。”在教学中，我们要谨记这一点，努力营造探究型课堂，促使学生在获得知识的同时，培养其探究能力。下面结合具体的教学实践浅谈一下如何培养初中生数学探究能力。

一、 设置问题，激发探究

鲍波尔曾说：“正是问题激发我们去学习，去实践，去观察。”疑问能激发学生的好奇心与求知欲，促使其主动参与到学习过程中，而要达到这种效果的最好方法是设置“新的需要与学生原有的数学水平之间存在着认识冲突”的問题情境，以此激起学生学习的兴趣，使之能快速投入到自主探索中去。

在课堂教学中，结合教学内容，捕捉“生活现象”“学生兴奋点”，精心设置问题情境，能激起学生的学习兴趣，拉近学生与新知的距离，从而激发学生探究新知的欲望。

二、 拓展时空，引导探究

新课标的核心理念，就是“强调课程的功能要从单纯注重传授知识转变为引导学生学会学习、学会生存、学会做人”。在教学过程中来，我们在激发学生积极、主动地参与到课堂中的基础上，要提供分组学习、开展讨论、陈述观点、做出论证的时间和空间，进而引导学生探讨，提升其逻辑思维能力。

例如在七年级讲解直角三角形全等的判定方法“HL”时，由于勾股定理还未学习，教材中是用画图、比较的方法得到结论的，即每个同学都画一个一条直角边和斜边分别相等的直角三角形，然后比较发现所有同学画出的三角形都是全等的，从而得到判定直角三角形全等的特殊方法“HL”。显然这种方法具有特殊性，不严谨，不利于学生逻辑思维能力的培养，所以在实际教学中我充分给予学生思考、讨论的时空，通过适时点拨的方式引导学生探究。

课堂中多留一点思考的时间给学生，往往会让我们有意外的惊喜，也有利于学生数学能力的提高。

三、 体验过程，学会探究

新课标指出“义务教育阶段的数学课程不仅要考虑数学自身的特点，更应遵循学生学习数学的心理规律，强调从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程”。教学实践告诉我们只有当学生通过自己的参与、思考建立起自己的数学理解力时，才能真正学好数学，并学会探究、学会学习。

例如在学完幂的几种运算后，学生容易出现混淆的情况，究其原因是学的时候对各运算法则没真正理解清楚。在实际教学中，要让学生亲自经历得到法则的过程，可先组织学生观察一系列的式子，让其猜测其中可能包含的运算法则，然后再验证猜测的正确性。整个过程始终让学生思考、交流、尝试，从而对于知识的获得有实际的理解和感受，印象自然深刻，并体验了“观察——猜测——讨论——动手操作——验证”这种探究性学习的基本方法。

四、 设计练习，强化探究

“学而时习之”“温故而知新”告诉我们温习的重要性，对于数学学科来说，最重要的温习方法是做练习题。数学练习是一种基础活动，是新的认知活动的一个必要条件，在练习过程中可加深了对知识的理解，学会分析、运用。设计层层递进、富有新意的练习可强化学生的探究性思维品质。

例如在复习平行四边形这一章内容时，可设计这样一个层层递进的练习题来加深学生对概念、定理的理解，并强化探究能力。

1.

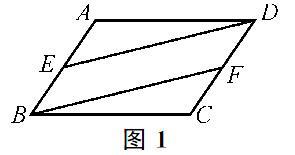
如图1，在ABCD中，E，F分别是AB，CD的中点，连接DE、BF。求证：四边形DEBF是平行四边形。

这是课本上的一个原题，放在这里主要是复习回顾，加强基础训练，并为后面的变式奠定基础。

2.

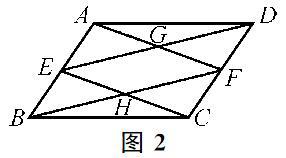
在图1的基础上，添加两条线AF、CE，AF与DE相交于点G，CE与BF相交于点H，如图2所示。求证：四边形EHFG是平行四边形。

经过观察、思考，不少学生发现了这个复杂图形中的类似于图1的两个基本图形：

易得四边形DEBF、四边形AECF是平行四边形。进而利用平行四边形的性质得到DE∥BF，AF∥CE，从而可得四边形EHFG是平行四边形。

3.

在此基础上，进一步引导学生探究若四边形EHFG是特殊的平行四边形，如菱形、矩形、正方形，那么一开始的条件中的ABCD还需满足什么条件？

在解答这个具有探究性的练习题时，学生既复习了相关知识，也加深了对概念、定理的理解，并学会了分析，提高综合运用能力，从而强化了探究能力。

21世纪的人才，需具有整体意识、创新精神、合作能力，而这些能力的培养可通过学生切实的探究活动来实现，所以在教学中我们要着力通过多种途径，让课堂充满生机与活力，使学生在获得知识的同时，树立探究意识，提升探究能力。

参考文献：

[1]任勇.任勇的中学数学教学主张[M].中国轻工业出版社，2012，3.

作者简介：

陈芳，江苏省苏州市，苏州工业园区星港学校。