初中几何识图能力的培养

摘 要：近年来，考查学生几何识图能力逐步增加，学生面对题目中提供几何图形不能理解，束手无策，识图能力较弱是重要原因之一。学生会看图、读图，有助于理解基本的数学概念，是学生几何素养的重要体现。

关键词：辨图;画图;赏图

一、 辨图——加强变式教学，辨析基本图形

《数学课程标准》在几何方面的学习要求学生“能从较复杂的图形中分解出基本的图形，并能分析其中的基本元素及其关系，利用直观来进行思考。”在初中教学中，距离最短问题一直贯彻在整个初中阶段。做这一类的题目的理论依据是两点之间线段最短，或者是利用轴对称的知识来解决。例题：如图1，AB两村在一条小河的异侧，要在河边建一水厂向两村供水。若要使自来水厂到两村的输水管用料最省，厂址Q应选在哪个位置？请将符合上述情况的自来水厂的厂址标出，并保留作图痕迹。

变式1：如图2，若AB两村在这条小河的同侧，若要使自来水厂Q到两村的输水管用料最省，应如何来作图？

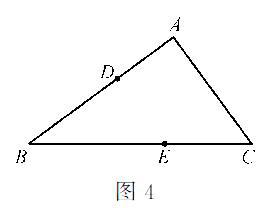
变式2：如图3，点D、E分别在△ABC边AB和BC上，请在AC上作一个点P，使△DEP的周长最小。

变式3：如图4，正方形ABCD的边长为4。E是AB边上的中点，P点在对角线AC上运动，求△PBE周长的最小值。

在上述题中，不断地改变问题的条件：在河同侧变为异侧，一条线变两条线，两条线变三条线（三角形）、四条线（正方形）问题，最终都可转化为例1教师引导学生遇到问题能从复杂的图形中分辨出基础图形。一方面老师在教学中，抓住基本图形中隐含的定理，应用变式教学强化基本图形;另一方面，引导学生对基本图形的理解不要浮于表面，透过现象看本质。

二、 画图——揭示定理本质，画“繁”为“简”

在几何题中，动点问题往往是令多数学生头痛的题，遇“动”则“不动”。究其原因，探索不出图形位置、数量关系的“变”与“不变”性，而这其中恰恰包含对象之间的几何和数量关系。

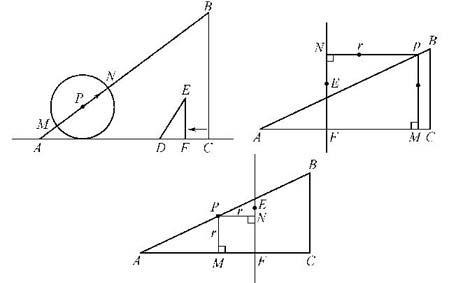
例如，如图，已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上，且AC=60cm，BC=45cm，DE=6cm，EF=8cm。现将点C与点F重合，再以4cm/s的速度沿CA方向移动△DEF;同时，点P从点A出发，以5cm/s的速度沿AB方向移动，设移动时间为t（s），以点P为圆心，3t（cm）长为半径的⊙P与AB相交于点M、N，当点F与点A重合时，Rt△DEF与点P同时停止移动。在移动的过程中，是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻？若存在，求出t的值;若不存在，说明理由。多数学生是纠结圆与两条直线相切的图形始终画不恰当，导致找不出等量关系。但若抓住切线性质定理的本质，会发现没必要画出圆。如图，分类出⊙P在直线EF的左侧、右侧两种情况后，原图中圆不必画出，只需过点P分别画垂直于EF、AC的垂线段，这两条垂线段的长度都为半径长，继而转化到AC线段，得出数量关系。

教师要引导学生解决动点问题画图策略：1. 全面地阅读题目。充分掌握运动的形式和方式，寻找到在运动中变与不变位置关系;2. 给图形適当地做“减法”。把在运动中导致图形本质发生变化的图形画出来，剔除干扰图形;3.

建立起对应的数学模型最终求解。总之，解决动态几何问题画图的关键是把握图形运动与变化的全过程，转化为静态图形，以不变应万变。

三、

赏图——借助几何画板，反思几何识图

几何画板是信息技术与几何教学整合的主要工具之一，其直观的动态演示功能，为学生搭建了探索几何图形内在关系的平台，提供给学对图形的感性认识，形成丰富的识图经验。当然，作为教师在这个过程中应引导学生动手画图思考，重点是演示之后学生的总结反思，让几何画板成为教学的工具之一，而不是完全依赖它。

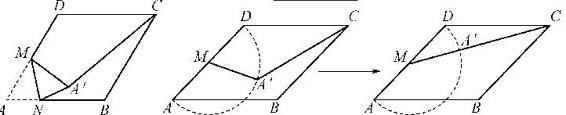
例如，如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，若线段MA绕点M旋转到线段MA′，连接A′C，则A′C长度的最小值是    。

先让学生尝试画出点A′的运动路线，待学生独立分析过后，教师再操作几何画板动态演示，师生共同从总结此题背后的基本图形：在圆上找一点A′，使得圆外点C离A′最近，即A′就是MC与圆的交点。针对此题，笔者引导学生做如下反思：

1.

思考过程的反思。通过教师分析及演示后，首先反思自身知识点提取是否熟练：本题涉及哪些重要知识点？然后反思方法是否熟练：用到哪种方法？解题思路是什么？今后遇到这类题又该如何解？最要总结其中的经验教训，批注重要的反思。这样使学生能够从不同角度观察图形，思考问题，养成勤于思考的习惯，提升识图能力。

2.

知识方法的反思。在我的思维活动中运用了哪些联想？它们是如何被想到的？我还能把它应用到什么情景中去。引导学生要善于把题目归类，找出题目中共性的地方，将基本图形画在此题的旁边。学生从中总结解题思路，掌握解题的技巧和方法，往往会达到事半功倍的效果。通过此题的研究，教师再举一反三加以巩固。

学生在教师为其提供的几何情境中经历发展过程，经历从具体到抽象、从特殊到一般的思维过程，把握数学知识的实质，通过自己辨图、画图，实现抽象知识图形化，复杂图形简单化。

作者简介：

鲍文碐，江苏省苏州市，太仓实验中学。