基于粒子群优化的年度合同电量降维分解模型

王良缘

（国网福建省电力有限公司，福建福州 350003）

市场化是电力深化改革的目标。为了电网的安全稳定运行，减少风险发生的可能性，当前中国的电力市场主要还是以合约交易为主，竞价上网为辅。通常在每年的年末，电网根据负荷预测曲线制定来年的发电计划。各个电厂将申报容量提交之后，电网公司对网络潮流进行安全校核，确保各条线路上没有发生堵塞，电网公司与各个电厂签订次年的年合约电量。电网公司再根据月度负荷预测曲线、热电联产、各个发电厂的最大最小发电量的约束及机组检修计划等情况，对年合同电量进行月度分解。例如，热电厂在冬季有供暖的要求，此时就有最小发电出力的约束；以及在丰水季节，为了避免清洁能源的浪费，也有对发电最小出力的约束；同时如果某个月某个电厂的发电机组遇到检修，相应月份的最大发电出力也应该相应地减小。由于预测不准确及机组故障等原因，实际发电量与计划发电量总会存在偏差，因此需要根据之前时段机组的完成情况，在后续的时段中对偏差电量进行滚动修正。合同电量分解得不得当，将会造成完成偏差大，执行困难，调峰能力不足等一系列的问题。恰当的合同电量分解能够大大减少电网调度的复杂性，降低实时市场的价格波动，对各个电厂参与日前市场和实时市场的公平竞争，对电力市场的稳定性有着重要的作用。

现有文献对于电力合同交易的交易模式[1-3]、风险控制[4-7]、竞价机制[8-9]等方面开展了很多研究，但对合同电量的分解问题研究相对较少。文献[10]将合约电量分解归纳为二次规划的优化问题，提出了能考虑检修、水电电量受限、热电联产等特殊问题的进度系数概念，并根据进度系数提出逐段法进行分解，使各个时间单元每个发电厂的进度系数尽可能保持均衡；文献[11]建立了一种基于二次规划的合同电量优化分解模型，该模型及算法能够保证各机组在不同时段发电进度的一致性，同时兼顾检修、热电联产等特殊情况，快速完成进行合同电量的自动分解；文献[12]通过浙江发电侧电力市场中合约电量的制定、分解的过程，提出适用于浙江电网的确定性合约电量分解算法、年度合约电量模型、负荷模型、计划检修处理模型和技术出力处理模型；文献[13]以华东电力市场为背景，提出一种基于电荷系统搜索（CSS）算法的年度合约电量分解方法；文献[14]提出一种火电机组月度合同电量分解算法，综合考虑机组月度检修计划调整、合同电量的滚动修正、发电与负荷之间的平衡、最大最小发电量约束等因素；文献[15]采用双因子非平稳序列方程和广义自回归条件异方差方程建立随机负荷模型，以合同电量比例与预定比例之差的标准差最小化为目标，以实际标准差小于预期标准差的概率为机会约束，构造了最优合同分解的随机规划模型，采用蒙特卡洛随机模拟和增广拉格朗日遗传算法相结合的方法求解。目前大部分的文献都以各个发电厂的发电均衡进度一致作为目标函数，或通过对分解结果进行滚动修正来使得各个发电厂的发电均衡进度尽可能一致。但大部分模型没有差异化地对待各个时间段及发电主体，难以得到真正均衡的分解结果；并且模型通常具有较大的决策变量维数，目标函数的求解依赖于这些决策变量，导致求解过程缓慢，容易造成维数灾的问题。

本文主要针对合同分解的决策变量维数多，容易造成维数灾而导致求解困难的问题，通过对约束条件的转换变形，将决策变量的维数降低；同时将离散的决策变量转化为对应的连续变量，利用粒子群算法对转化后的连续变量进行迭代寻优，从而解决了粒子群算法无法对离散变量进行优化的问题，大大提高了分解模型的效率和实用性。

1 合同电量的分解模型

本文先是引出发电利用率的概念，然后在考虑每个发电厂发电利用率均衡的基础上，对每个时段进行了差异化处理，体现决策者对不同时段的重视程度，使得目标函数即发电利用率均衡一致。其次，描述了对本模型的约束条件，同时利用约束条件将离散的发电利用率转化成连续的变量，进而利用粒子群算法进行优化。

1.1 发电利用率

在分解过程中，为保证电网调度的易操作性和市场运行的公平性，决策者要考虑在不同的时间进度上，每个发电主体本身机组的利用率要大致相同，这样才能保证电网的安全经济运行及协调性。本文将发电主体本身机组的利用率定义为发电利用率，具体表达式为

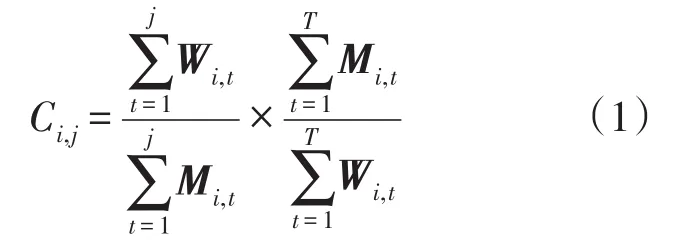
式中：i表示第i个发电厂；j表示第j个时段。发电利用率Ci,j的含义是：前j个时间单元内第i个发电厂的发电利用率，Ci,j能够客观反应各个发电厂在前j个时段机组设备的利用率。通过将各个发电厂的发电利用率安排得尽可能一致，能够在一定程度上体现出公平性。发电利用率过高会导致发电主体调峰和调度的困难，降低机组的灵活性，给日前市场和实时市场预留的空间不足，容易造成日前市场和实时市场的电价波动较大，导致市场的不稳定，在一定程度上缺失了公平性。发电利用率过低容易导致机组启停次数过多，造成发电主体的启停成本和维护成本增加，直接损害了发电厂商的利益。所以将发电利用率控制在一个合理的范围内，对于电网的调度安全和发电商的经济运行都有益，并且可保证分解结果易于执行，实现双赢。

1.2 合同电量分解的目标函数

在实际运行过程中，将每个发电主体发电利用率与全网的加权平均发电利用率相比较，如果没有偏离平均值很大的发电主体，且每个发电主体的机组利用率变化趋势与平均机组利用率相对一致，说明分解结果对于电网是友好的，可接受的；对于每个发电主体而言是经济的，合理的。本文将每个发电主体各个时段的发电利用率与该时段所有发电主体的加权平均发电利用率的偏移程度最小化作为目标函数，具体表达式为

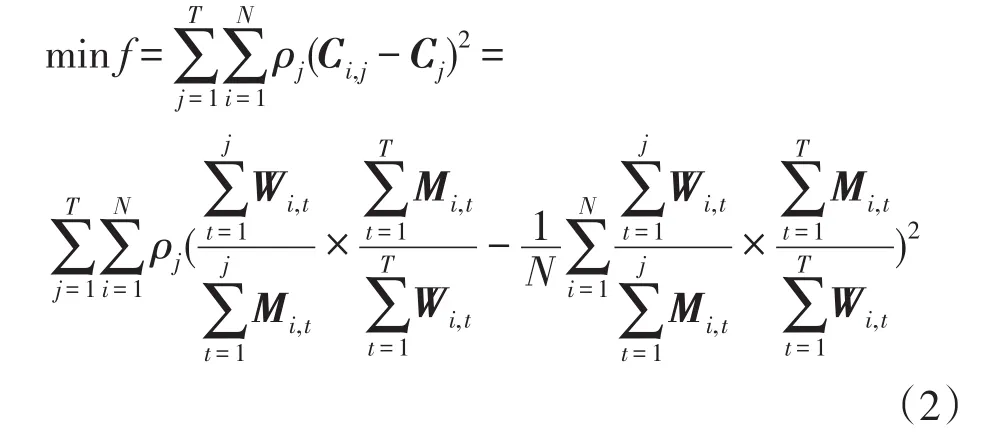
式中：Wi,t表示第i个发电厂第t个时段的分解值；Mi,t是第i个发电厂第t个时段的最大发电量；表示第j个时段的发电利用率加权和的平均值；ρj是加权系数，表明决策者对于不同时段不同发电主体的偏好程度，具有较高的灵活性。

1.3 模型的约束条件

合约电量在执行过程中需要考虑诸多约束条件，例如要考虑根据历史数据及大用户申报负荷电量的情况来预测负荷曲线，考虑每月通过竞价的方式产生的月度新增电量，合约电量的分解结果与通过竞价产生的月度新增电量一起作为每月的发电计划。还要考虑机组最大最小出力的约束，每个发电主体签订年度合同电量的约束等。本文将考虑以下约束条件：

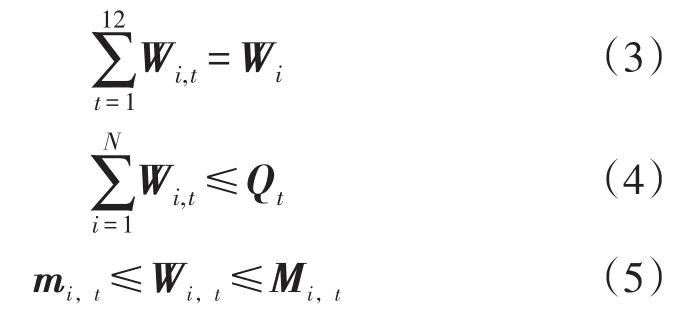
式中：Wi表示第i个发电厂的年合同电量；Qt表示第t个月的总合约电量的可分解值；Mi，t，mi，t分别是第i个发电厂第t个时段的最大最小发电量，由机组容量大小、故障情况、检修状态和季节特殊性来决定。式（3）表示的是每个发电厂的年度合约电量平衡约束；式（4）表示的是根据月度负荷预测的月度负荷的约束，即在同一个月内，所有电厂发出来的电不可以多于这个月的预测负荷量，其中不足的电量可在日前市场和实时市场购买。

2 基于粒子群的降维求解方法

由式（3）和式（4）可知，该模型有i个等式约束和T个不等式约束，约束条件较为苛刻，找到可行解效率较低。本文通过适当减小不等式右边的值，将不等式约束转化为等式约束，从而将问题转化为等式约束规划。然后利用（i+T）个等式求解出通解，将离散的决策变量转化为连续的决策变量，同时实现维数的降低，提高模型的求解速度。假设要调度的发电厂有n个，分解的时段有m个（本文是年度合同电量向月度分解，所以m为12），那么需要分解得到的变量就有n×m个，此时优化变量维数较大，容易造成维数灾的问题，使得模型不好求解。首先假设式（2）的等式成立，并且假设待分解的变量为Wi,t，那么结合式（1）可列出年度电量和月度电量的约束，以矩阵形式表示为

式中：A是(n×m)×(n+m)阶的十分稀疏矩阵，A的前n行为年度合约的等式约束，后m行为月度负荷预测的不等式约束。Wi,t是(n×m)×1阶的待分解量，b是(n+m)×1阶的约束，b的前n个值为年度合约的等式约束，后m个为月度负荷预测的不等式约束。当矩阵A的秩与增广矩阵相同且等于(n+m)时，式（6）有唯一解；当矩阵A的秩与增广矩阵相同且小于(n+m)时，式（6）的解不唯一，可以表示成通解的形式，即

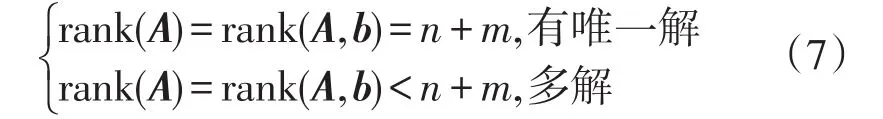
由于式（2）的约束条件为各个发电厂每个时段的出力和小于每个时段的负荷量，所以当式（6）难以求出解时，可适当减小b的后m行的值，直到满足rank(A)=rank(A,b)，此时可用矩阵表示为

式中：b′为b的后m行修正后的值。此时可以根据式（8）求出Wi,t的通解表达式为

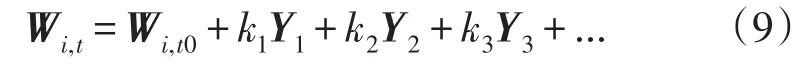
式中：Wi,t0是式（8）的一个特解；k1、k2、k3等是常数；Y1、Y2、Y3等是式（8）的右边的b′赋 0，从而得到的方程组的解的每一列。

求出式（8）的通解后，又由于有发电机最大最小出力的约束，即每一个Wi,t都有一个范围，此时再根据公式（5）求各个k的取值范围，这时k只有(n×m)-rank(A)维，使得维数降低了不少，从而再用粒子群算法在这些范围内更新迭代，求出最优值。利用该方法，能够将原来的离散域的更新迭代转变为k的连续域的更新迭代，使得求解速度更快，更易满足条件。在此基础上，适当调整月度分解电量值Qt，使得Qt适当小于约束值，之后再用粒子群算法寻优迭代，找出最佳的目标函数值。算法流程如图1所示。

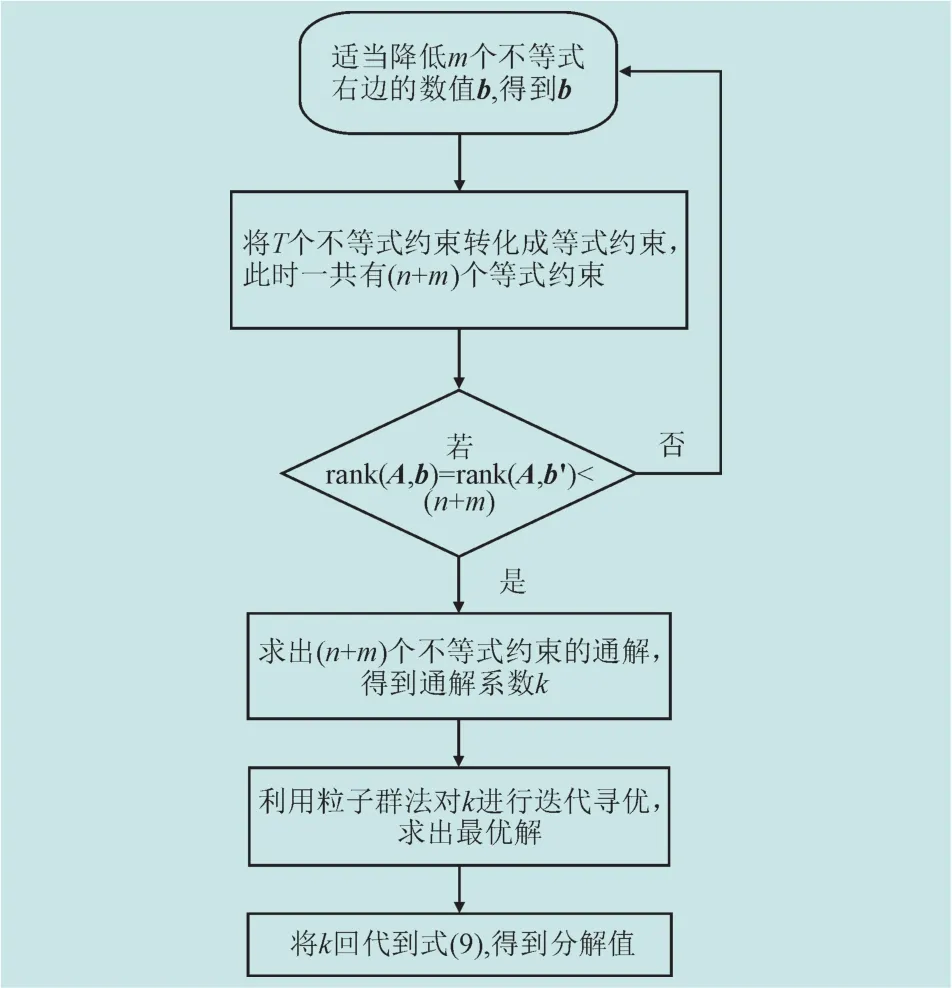
图1 算法流程图Fig.1 Flow chart of the algorithm

在求解决策变量的过程中，由于决策变量的数量较多，导致求解过程缓慢，甚至可能出现无解的情况。该方法的主要优点在于能够大大降低决策变量的维数，使求解速度有较大的提升。

3 偏差电量的滚动修正

由于负荷预测的不准确等原因，以及计划发电量与实际发电量总会有误差，所以偏差电量的产生是不可避免的。传统的偏差电量处理方式是为了增加各个机组在年末各月的调度空间，增强整个电网的调度能力，将某月产生的偏差电量按照负荷曲线分配给余下的月份。这样一方面能够保证对每个机组调峰能力的公平性，同时也可以考虑到在不同负荷大小的情况下偏差电量分配的大小，从而起到削峰填谷的作用。假设第t0-1月之前的电量已分解滚动完毕，满足了横向约束及纵向约束。横向约束即每个发电厂的年合同电量，纵向约束为每个月的月度负荷约束，即每个发电厂每个月所发电量的总和不能超过每个月的总负荷。那么假设第t0-1月产生了偏差电量，即

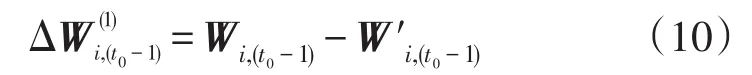
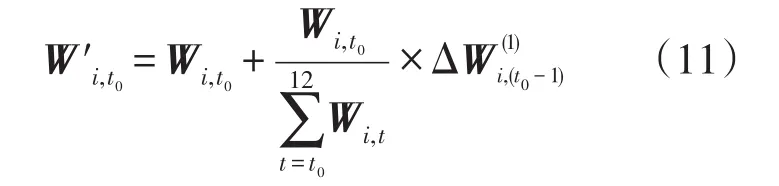
这样的处理方式虽然能够体现公平性，但是由于有发电机最大最小出力的限制，后续的月份若不能够将偏差电量进行处理，会继续将偏差电量往后滚动。此时第t月的电量冗余值为

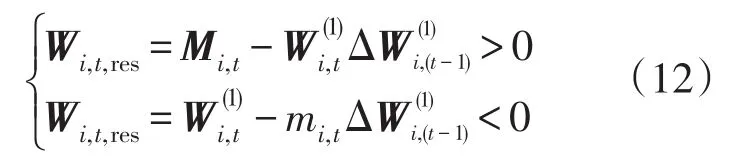
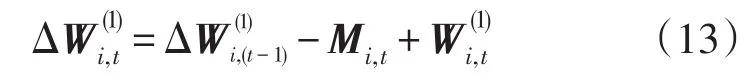
若t+1的冗余电量值大于此时的偏差值，则偏差电量由t+1月承担，否则滚动至下一个月来执行。

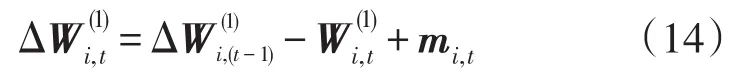
若t+1月的冗余电量值大于此时的偏差值，则偏差电量由t+1月承担，否则滚动至下一个月来执行。进行横向修正后的发电厂年度合同电量的约束都能得到满足。

4 算例计算与分析

以3座典型火电厂为例，将这些火电厂签订的年度合同电量（见表1）分解到各月（由月分解到日类似），假设每个发电厂的月发电量在10 000MW∙h到100 000MW∙h之间不等。每个月的需求电量根据历史数据及用户提交的负荷曲线进行预测，假设如表2所示。粒子群算法的迭代次数设定为100次，利用matlab软件进行仿真。

表1 每个发电厂签订的年度合同电量Table 1 Annual electricity contract signed by each power plant MW·h

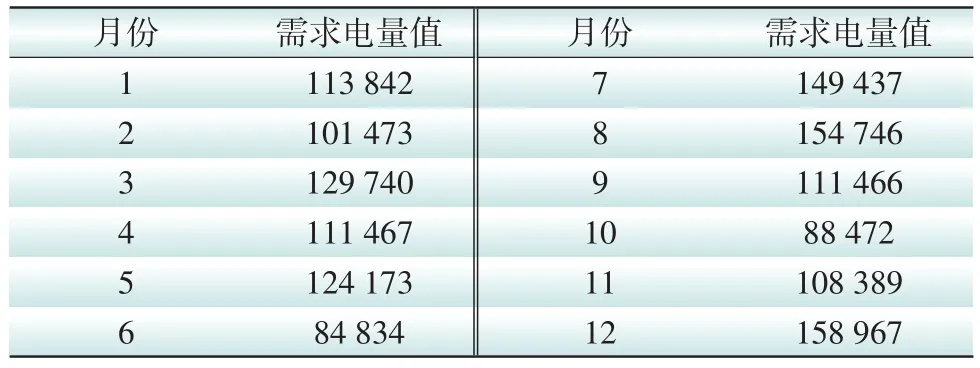
表2 每个月的负荷预测值Table 2 Load forecast per month MW·h

根据式（4），由于每个月的可分解电量是一个小于等于的关系，分别假设每个月的可分解电量在95%～100%、90%～100%和85%～100%的需求电量之间，将该月未发的计划电量滚动至后续月份来执行，从而寻找出使得目标函数值最优的月分解电量。根据2.1节的分析，3种不同情形下得到的结果分别如图2、图3和图4所示。

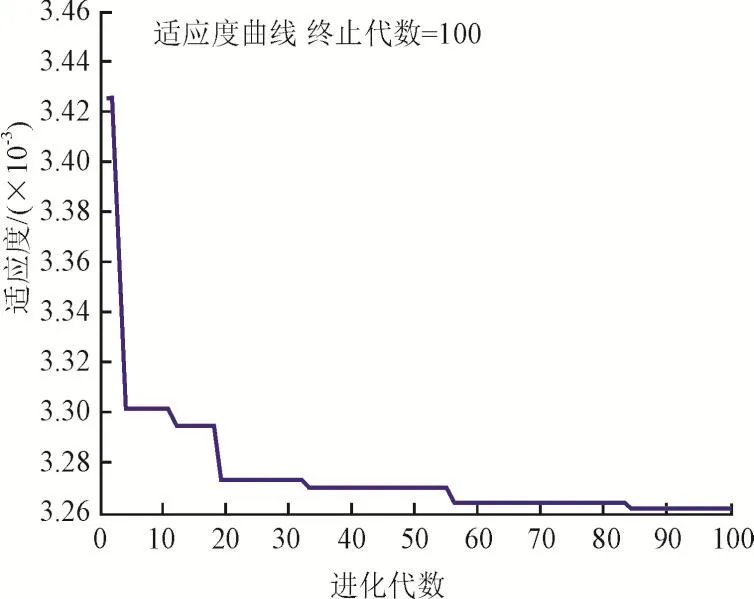
图2 在需求电量95%～100%范围内优化时目标函数的迭代曲线Fig.2 The iterative curve of the objective function in the range of demand electricity（95%～100%）

对比图2、图3和图4中的3条迭代曲线可以看出，随着对式（4）右端值下降的幅度越大，目标函数的最优值也逐渐变大。并且在优化的过程中，粒子的更新也很容易陷入局部最优，甚至在需求电量为85%～100%范围内优化时，目标函数值从始至终都没有更新过，从而该模型也失去了它的优越性。所以本文假设在需求电量为95%～100%的范围内优化，从而得到最优的目标函数值。分解结果如图5所示，月度需求电量曲线如图6所示。

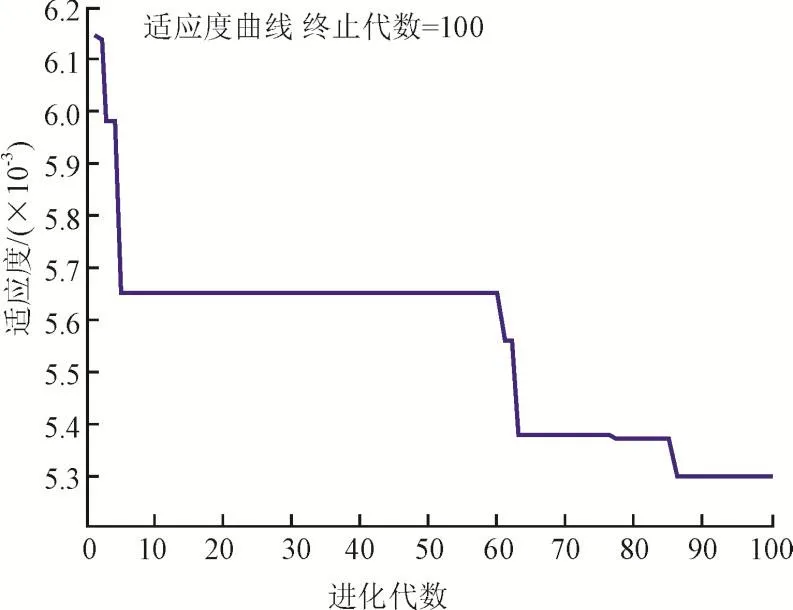
图3 在需求电量90%～100%范围内优化时目标函数的迭代曲线Fig.3 The iterative curve of the objective function in the range of demand electricity（90%～100%）

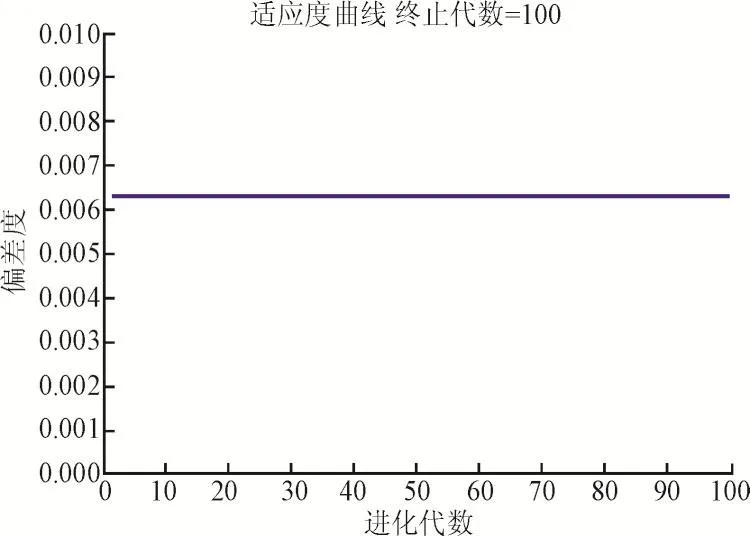
图4 在需求电量85%～100%范围内优化时目标函数的迭代曲线Fig.4 The iterative curve of the objective function in the range of demand electricity（85%～100%）

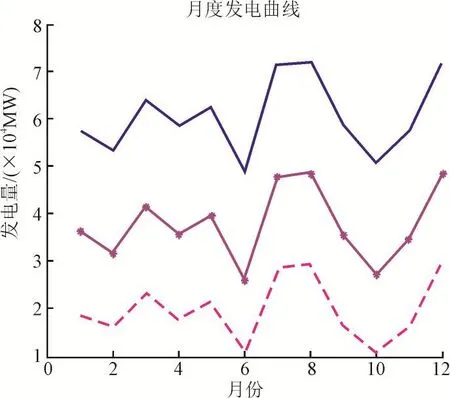
图5 分解结果Fig.5 Analysis results

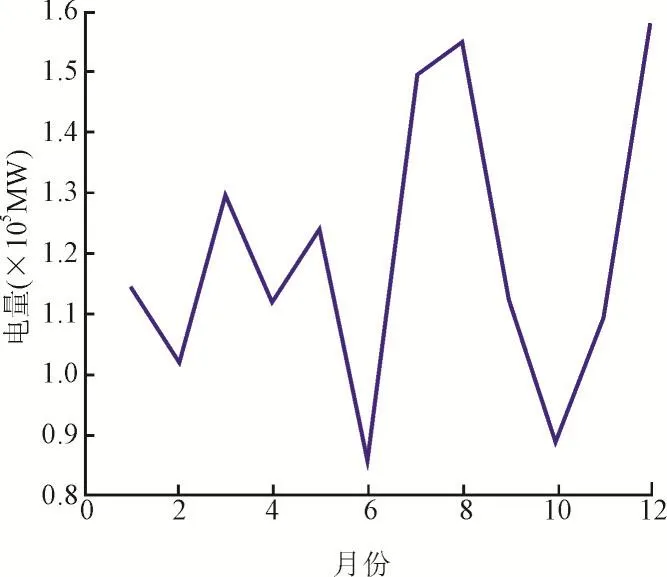
图6 需求电量曲线Fig.6 Electricity demand curve

从图2目标函数的迭代曲线可以看出，目标函数值在迭代到84次左右时收敛于一个稳定值，说明该解法具有较快的收敛性。从分解结果可以看出，3个发电厂每个月份的发电量总和都没有超过可发容量的限制，同时留有一定的备用容量；同时，对于每个发电厂来说，每个月份发电量的总和等于签订的年度合同电量，说明分解结果能够保证每个发电厂按照合约规定完成任务。从3个电厂的发电曲线可以看出，每个电厂的发电走势与电量需求的走势相似，说明分解结果是合理的。这样的分解结果不会在电量需求较高的月份发电不足，导致实时市场和平衡市场的电价波动大；也不会在电量需求较低的月份大量发电，导致发电剩余，具有实用性。

5 结论

本文针对电网中存在的年度合同电量分解的需求提出了合同分解的模型。在借鉴前人研究的基础上，将容易造成维数灾的决策变量降维化，使得决策变量的维数得到较大的降低，使求解过程及求解结果加快提升。同时，本文就电网中出现的偏差电量提出了修正模型，将产生的偏差电量根据负荷曲线分配到剩余的时段，使得修正后的发电曲线与负荷曲线尽可能一致。通过对算例结果的分析，验证了模型的合理性和科学性。

[1] 邰雪，孙宏斌，郭庆来.能源互联网中基于区块链的电力交易和阻塞管理方法[J].电网技术，2016，40（12）：3630-3638.TAI Xue，SUN Hongbin，GUO Qinglai.Block trading and congestion management method based on block chain in energy internet[J].Power System Technology，2016，40（12）：3630-3638.

[2] ZHOU Zhi，LIU Fangming，LI Zongpeng.Bilateral electrici⁃ty trade between smart grids and green datacenters:pricing models and performance evaluation[J].IEEE Journal on Se⁃lected Areas in Communications，2016，34（12）:3993-4007.

[3] 王维超，薛宇，李更丰，等.电力能效统筹的市场交易体系及保障机制研究[J].电网与清洁能源，2017，33（2）：1-7.WANG Weichao，XUE Yu，LI Gengfeng，et al.Research on market trading system and security mechanism of power energy efficiency overall planning[J].Power System and Clean Energy，2017，33（2）：1-7.

[4] 方日升.考虑风电的省级电网多类市场购电风险研究[J].电网与清洁能源，2017，33（4）:113-118.FANG Risheng.Research on multi-market power purchas⁃ing risk of provincial grid considering wind power[J].Power System and Clean Energy，2017，33（4）:113-118.

[5] 赵阳，蒋传文，赵岩，等.基于偏度-加权条件风险价值的售电公司动态购电策略[J].电网与清洁能源，2017，33（1）:130-136.ZHAO Yang，JIANG Chuanwen，ZHAO Yan， et al.Skewness-WCVaR based dynamic procurement strategy forelectricity retailers[J].PowerSystem and Clean Energy，2017，33（1），130-136.

[6] 马歆，蒋传文，侯志俭，等.电力金融合约市场及其风险控制研究[J].华东电力，2002（9）:8-10.MA Xin，JIANG Chuanwen，HOU Zhijian，et al.Study on financial contract market and the risk control of power[J].East Power，2002（9）:8-10.

[7] 刘春辉，刘敏.直购电环境下基于E-CVaR的电网公司风险控制策略研究[J].电网与清洁能源，2010，26（12）：42-46.LIU Chunhui，LIU Min.Risk control strategies based on E-CVaR for power gird companies under direct electricity purchasingenvironment[J].PowerSystemandCleanEnergy，2010，26（12）:42-46.

[8] WANG Yao，AI Xin，TAN Zhongfu，et al.Interactive dis⁃patch modes and bidding strategy of multiple virtual power plants based on demand response and game theory[J].IEEE Transactions on Smart Grid，2016，7（1）:510-519.

[9] 舒畅，钟海旺，夏清.兼顾效率与公平的用电市场竞价机制研究[J].电网技术，2014，38（3）：681-686.SHU Chang，ZHONG Haiwang，XIA Qing.Taking into account the efficiency and fairness of the design of electricity market bidding mechanism[J].Power System Technology，2014，38（3）：681-686.

[10]黎灿兵，胡亚杰，赵弘俊，等.合约电量分解通用模型与算法[J].电力系统自动化，2007，31（11）：26-30.LI Canbing，HU Yajie，ZHAO Hongjun，et al.General model and algorithm for contract energy decomposition[J].AutomationofElectricPowerSystem，2007，31（11）：26-30.

[11]王冠群，刘锋，梅生伟，等.合同电量优化分解模型及算法［J］.电机与控制学报，2012，16（7）：58-64.WANG Guanqun，LIU Feng，MEI Shengwei， et al.Optimal decomposition model and algorithm of contract electricity quantity[J].Journal of Electrical Machinery and Control，2012，16（7）：58-64.

[12]戴铁潮，张丹.确定性合约电量分解算法在浙江发电市场的应用[J].华东电力，2000，28（10）:7－9.DAI Tiechao，ZHANG Dan.Application of deterministic contract energy decomposition algorithm in Zhejiang power generation market[J].East Power，2000，28（10）:7－9.

[13]张少迪.基于CSS的年度合约电量分解方法[J].电力自动化设备，2014，34（11）:135-141.ZHANG Shaodi.Annual contract quantity decomposition method based on CSS[J].Electric Power Automation Equipment，2014，34（11）:135-141.

[14]温丽丽，刘俊勇，吴志云，等.基于月度滚动修正的合同电量算法与应用[J].现代电力，2008，25（1）：83-87.WEN Lili，LIU Junyong，WU Zhiyun，et al.Algorithm and application of contract power based on monthly rolling correction[J].Modern Power，2008，25（1）：83-87.

[15]陈建华.中长期差价合同分解及相关问题的研究[D].杭州：浙江大学，2008.