高压星形密封圈的密封性能分析

王冰清，余三成，孟祥铠，李 勇，李纪云

（1.浙江工业大学过程装备及其再制造教育部工程研究中心，浙江杭州 310032；2.上海航天控制技术研究所，上海伺服系统工程技术研究中心，上海 201109）

1 前言

星形密封圈由O形密封圈演变而来，是一种具有四唇密封截面的密封元件，因形状类似字母“X”又称为X形密封圈。与O形圈相比，星形密封圈的摩擦系数低、抗扭转效果好，密封唇间形成了润滑容腔，适合应用于流体机械的动密封场合［1,2］。

在高压（＞10 MPa）条件下，为避免星形密封圈因流体压力作用被挤入沟槽间隙而引发密封失效的危险，可通过加矩形挡圈来缓和密封圈的应力集中。目前国内外学者对往复密封系统用星形圈的研究主要集中在无挡圈方面，而关于带挡圈的星形密封圈的研究较少［3～11］。虽然在工程实际应用过程中通过施加挡圈提高了星形密封圈在高压条件下的密封使用寿命，但由于缺乏对加挡圈密封结构的密封机理等方面的准确了解，在一些极端工况下密封圈依然存在着撕裂破坏和磨损失效的现象。

本文利用ANSYS软件研究不同流体压力、预压缩率和摩擦系数下，带聚四氟乙烯挡圈的丁腈橡胶星形密封圈的静、动态密封性能及其演变规律。从而揭示加挡圈的星形密封圈的密封机理和密封性能，并判定其易发生失效的部位，以期为往复机器用密封系统的结构设计提供理论指导。

2 有限元模型

2.1 几何模型

图1所示为带挡圈的星形密封圈的结构及其有限元二维轴对称仿真模型，主要由挡圈、星形圈和活塞杆3部分组成；密封圈结构尺寸为Ф 37.7 mm × 2.62 mm，沟槽形式为矩形槽，沟槽底圆弧倒角为0.1 mm，沟槽口圆弧倒角为0.2 mm，槽深为2.3 mm，宽度为4.5 mm；挡圈和活塞杆密封间隙为0 mm。虚线Ⅰ为星形圈截面中心线，是内侧和外侧的分界线；虚线Ⅱ为压力侧和非压力侧的分界线。规定活塞杆运动方向与星形圈受油压方向一致的过程定义为上行过程（或外行程），反之为下行过程（或内行程）；星形密封圈与活塞杆接触的配副界面为主密封面，与沟槽接触的配副界面为副密封面。

图1 带挡圈星形密封圈结构及其仿真模型

2.2 有限元前处理

挡圈材料为聚四氟乙烯复合材料，弹性模量E=1000 MPa，泊松比ν=0.3［12］；星形密封圈材料为丁腈橡胶，弹性模量为7.8 MPa，泊松比为0.498；活塞杆材料为铝合金材料。在有限元分析中，由于铝合金材料的弹性模量远大于橡胶材料的弹性模量，因此可以将活塞杆视为刚体材料。

橡胶密封圈的材料是一种超弹性材料，具有高度的几何非线性、材料非线性和接触非线性三重非线性特性［6］。本文采用目前广泛采用的Mooney- Rivlin模型来描述橡胶材料的应变能函数，其二参数应变能函数式为：

式中 I1，I2——Green应变不变分量

C10，C01—— Mooney-Rivlin常数，其值分别为1.9641 和 0.4691［13］

星形橡胶密封圈和矩形挡圈均选用超弹体平面四节点单元PLANE182，密封副接触方式均为面-面接触，接触类型为刚-柔接触，接触单元类型为CONTA172，目标单元类型为TARCE169。接触算法采用加强的拉格朗日法。

3 有限元分析结果

3.1 静压工作状态

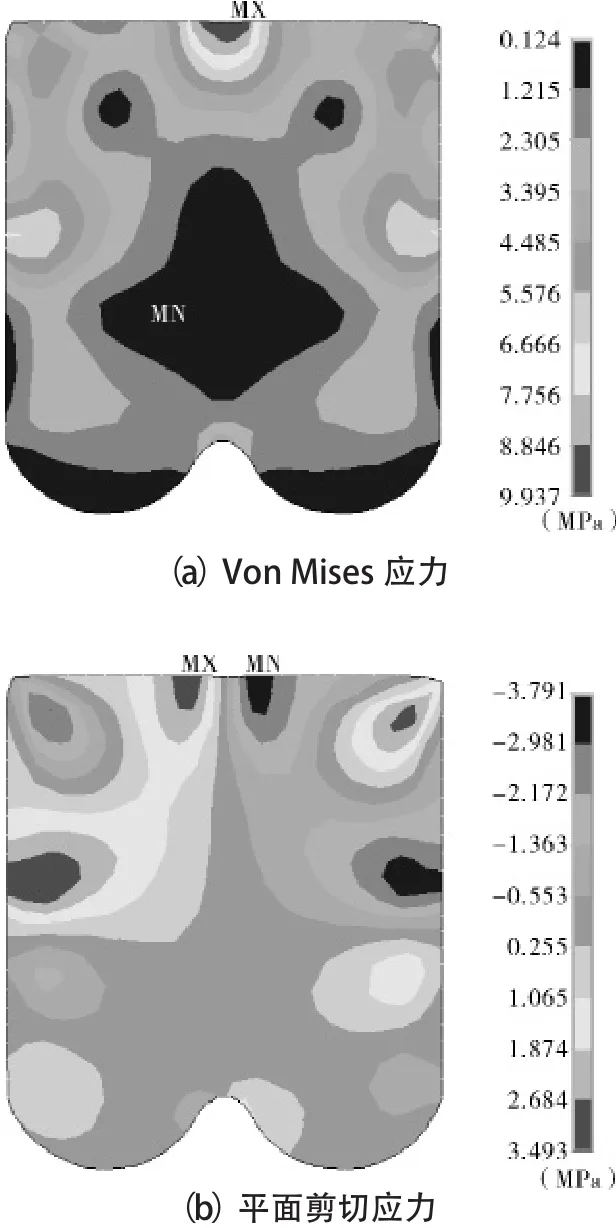
图2 静压状态下星形密封圈的Von Mises应力和平面剪切应力云图

图2 和图3所示为星形圈在预压缩率为12%、流体压力为24 MPa、主密封面摩擦系数为0.25的工况下所受各种应力的分布云图。从图2看出，星形圈的Von Mises应力和平面剪切应力均按截面中心线呈对称分布；最大Von Mises应力值9.937 MPa，最大剪切力值-3.791 MPa，都发生在非压力侧凹圆处。其中，剪切力负值表示方向与xy平面规定的正方向相反，当剪切应力超过橡胶材料允许的剪切强度时，星形密封圈会发生剪切撕裂破坏失效。从图3可以看出，星形圈的主、副密封面上的接触压力按截面中心线基本呈对称分布，主密封面最大接触压力值为29.533 MPa，发生在压力侧的内侧凸圆处，保证了足够长的密封区域。摩擦应力表征了密封圈表面所受摩擦力大小，在一定程度上反映表面是否存在磨损失效的危险。星形圈的主、副密封面上的接触摩擦应力按截面中心线基本呈对称分布，其数值分布范围为-2.949～3.555 MPa，最大摩擦应力发生在非压力侧的外侧凹圆处，最大值为3.555 MPa。

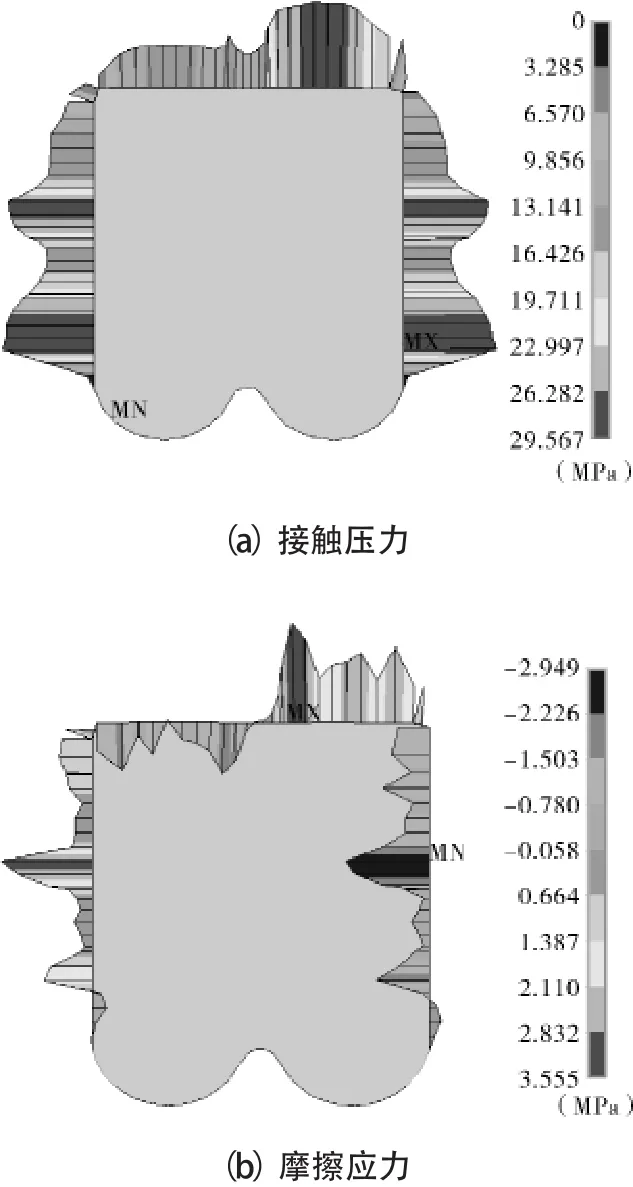
图3 静压状态下星形圈的接触压力和摩擦应力云图

3.1.1 流体压力

取星形密封圈的压缩率为12%，主密封面的摩擦系数为0.25，分析流体压力在12～24 MPa范围变化时星形圈的各应力分布情况。

在预压缩率及流体压力作用下，静止星形圈的最大Von Mises应力都出现在非压力侧凹圆弧处，且随着流体压力的增加呈现略微下降的趋势，如图4所示。这是由于随着流体压力的增加，挡圈的最大Von Mises应力呈线性增加的趋势，最大值出现在挡圈与沟槽口倒角接触处；随着流体压力的增大，星形圈和挡圈贴合越紧密，其接触面上的应力分布越均匀，从而有效缓和了星形圈的应力集中现象。同样，随着流体压力的增加，挡圈的最大平面剪切应力逐渐增加，而星形圈却基本保持不变。由此可知，在高压条件下，挡圈的安装可有效地缓和星形圈的应力集中，降低橡胶材料的剪切破坏几率。

图4 各应力与流体压力的关系曲线

由图4可知，随着流体压力的增加，星形圈主密封面最大接触压力呈线性增加趋势；且最大接触压力恒大于流体压力，满足密封要求。

图5所示为在不同流体压力下星形圈主密封面上的接触压力分布曲线，对主密封面上的节点重新编号，由非压力侧1#至压力侧30#，节点16#为非压力侧和压力侧分界点。星形圈主密封面上的接触压力含有两个大小接近的峰值，且最大接触压力在各流体压力作用下均大于其流体压力，能保证密封圈具有良好的密封性能。在12～24 MPa高压条件下，星形密封圈的非压力侧和压力侧间凹圆部位的空隙将不复存在，最大接触压力出现在靠近压力侧的凸圆处。

图5 不同流体压力下主密封面接触压力曲线

3.1.2 预压缩率

取星形圈的流体压力为24 MPa，摩擦系数为0.25，分析预压缩率在8%～10%时密封圈的各应力分布情况。

在流体压力恒定的情况下，星形圈的最大Von Mises应力随预压缩率的增大而增大，而最大剪切应力基本保持不变；最大Von Mises应力和最大剪切应力均出现在非压力侧凹圆处，如图6所示。挡圈的最大Von Mises应力出现在其与沟槽口倒角接触处；由于随着压缩率的增加，活塞杆与沟槽口间挡圈的高度逐渐减小，从而引起挡圈的Von Mises应力值呈整体下降的趋势。但是当压缩率为12%时，挡圈的最大Von Mises应力值却突然增大，原因是挡圈和星形圈接触面上接触应力的等效集中力作用点最接近沟槽口附近所致。当压缩率大于10%时，挡圈的最大剪切应力基本无变化，说明最大平面剪切应力主要与流体压力大小相关。

图6 各应力与预压缩率的关系曲线

由图6可知，随着密封圈预压缩率的增加，星形圈主密封面上的最大接触压力逐渐增加。

图7所示为几种典型预压缩率下星形圈主密封面接触压力分布曲线。

图7 不同预压缩率下主密封面接触压力曲线

由图可知，密封圈压缩率的改变并不会影响星形圈主密封面上接触压力分布曲线的形状，最大接触压力位于靠近介质侧的凸圆处，且均大于流体压力，满足静密封要求。

3.1.3 摩擦系数

取流体压力为24 MPa、密封圈压缩率为12%，在摩擦系数为0.1～0.5时星形密封圈各应力的变化情况如图8所示。

可以看出，随着摩擦系数的增加，星形圈的最大Von Mises应力和最大平面剪切应力均逐渐增加，而挡圈的最大Von Mises应力和最大平面剪切应力均呈逐渐下降的趋势。这是由于当流体压力一定时，主密封面摩擦系数的增加会阻碍因流体压力对星形圈的压缩而导致其变形产生的应力向挡圈传递。

图8 各应力与摩擦系数的关系曲线

此外，随着摩擦系数的增加，星形圈主密封面上的最大接触压力有缓慢增加的趋势，但幅度不大，说明在一定摩擦系数范围内，增大摩擦系数值可以增加星形圈的静密封能力，却越容易导致密封圈发生磨损失效。

图9所示为5种典型摩擦系数下星形圈主密封面上接触压力分布曲线。可以看出，活塞杆与星形圈接触区域上摩擦系数的改变并不会影响主密封面上接触压力曲线分布的形状。摩擦系数增大，星形圈主密封面上分界线Ⅱ处凹圆的接触应力反而减小。这是由于压力侧橡胶材料受流体压力挤压作用基本不受摩擦系数影响；而摩擦系数越大，非压力侧橡胶材料受摩擦力阻碍作用越明显，从而引起内侧凹圆区域产生远离活塞杆的趋势越明显，并导致该处接触压力有所减小。

图9 不同摩擦系数下主密封面接触压力曲线

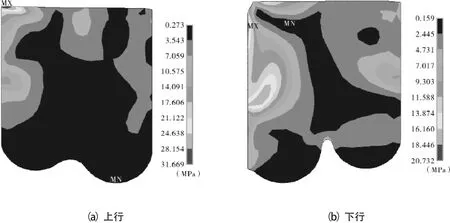
图10 活塞杆上行和下行时星形圈的Von Mises应力云图

3.2 往复工作状态

当流体压力为24 MPa、密封圈预压缩率为12%、密封副界面摩擦系数为0.25且活塞杆往复运动周期性振幅值为0.5 mm时，活塞杆上行（沿y轴正方向运动）或下行（沿y轴负方向运动）状态下的各种工作应力状态分别如图10，11所示。

由图10可知，当活塞杆上行时，星形密封圈的Von Mises应力分布变得不再均匀，其最大值31.669 MPa发生在星形圈非压力侧的内侧凸圆45°分界线处；当活塞杆下行时，最大Von Mises应力20.732 MPa发生在非压力侧的内侧凸圆45°分界线偏挡圈侧。

图11 活塞杆上行和下行时星形圈的剪切应力云图

当活塞杆上行时，星形圈非压力侧的内侧凸圆处受到的剪切作用最大，数值为-9.684 MPa；下行时，最大值10.05 MPa出现在星形圈内侧凹圆处，如图11所示。由图12可知，在活塞杆上行或下行过程中，星形圈的最大接触压力均发生在主密封面上，位于非压力侧的凸圆处；上行时最大接触压力为31.386 MPa大于下行时最大接触压力为29.877 MPa，且均大于密封流体压力24 MPa，密封性能可靠。由于PTFE挡圈的存在，在往复密封工作状态过程中星形密封圈并不存在被挤入密封间隙的危险。

图12 活塞杆上行和下行时星形圈的接触压力云图

上行和下行时星形圈的最大滑动摩擦应力均位于主密封面上非压力侧凸圆处，上行时最大值为 -7.63 MPa，下行时最大值为 7.469 MPa，如图13所示。星形圈主密封面上的应力值明显大于副密封面，非压力侧的内侧凸圆与挡圈接触的圆弧段区域在上行和下行过程中，滑动摩擦应力值变化幅度最大，从一定程度上反映了该区域存在磨损失效的危险。

图13 活塞杆上行和下行时星形圈的接触摩擦应力云图

从上述往复运动的分析可知，在高压条件下，加挡圈的星形密封圈的高应力区域主要集中在非压力侧的内侧凸圆靠近挡圈处以及内侧凹圆处，且密封圈的内部应力分布表现为内侧的应力值明显大于外侧。结合四种典型应力分布图可知，星形圈非压力侧的内侧凸圆靠近挡圈区域存在着易磨损失效的趋势，内侧凹圆处存在撕裂破坏的危险。上行过程中各应力值大小均大于下行过程，这是由橡胶材料有类似与流体的性质决定的，上行时活塞杆运动方向与流体压力一致，促进了密封圈材料向上的流动及其对挡圈的挤压变形；相反，下行时减缓了密封圈材料向上的流动，减缓了密封圈或挡圈的应力集中［4］。

4 结论

（1）在静压工作状态下，带挡圈的星形密封圈的最大Von Mises应力随着流体压力的增大呈现略微下降的趋势，但随预压缩率、摩擦系数的增大而增大；随着流体压力、预压缩率和摩擦系数的增大，星形圈主密封面上的最大接触压力均增大，且流体压力的变化对接触压力的影响最为明显。

（2）在往复工作状态下，当流体压力为24MPa、预压缩率为12%、活塞杆和密封圈接触的配副界面摩擦系数为0.25时，星形密封圈的内部应力值比静态时明显增大，且上行时的应力值大于下行，内侧应力值大于外侧，且分布十分不均匀。

（3）通过对带聚四氟乙烯挡圈的丁腈橡胶星形密封圈在静压工作状态以及往复工作状态下进行有限元模拟，分析得出：在高压条件下，星形密封圈的非压力侧的内侧凸圆靠近挡圈区域易发生磨损失效；内侧的凹圆弧部位易发生撕裂失效。

［1］ 程谟贵.X形橡胶密封圈的模具设计及加工［J］.特种橡胶制品 , 2000（2）: 50-52.

［2］ 余海燕,雷中清,冯强,等.滑套密封技术分析与性能评估［J］. 润滑与密封 , 2015, 40(3): 98-102.

［3］ 胡玉敏,常国振. 氨泵机械密封的泄漏原因与改进［J］. 流体机械 , 1996, 24(11): 44-45, 57.

［4］ 侯珍秀,余志洋,刘云猛,等.X形丁腈橡胶密封件的有限元分析［J］.宇航材料工艺,2007（6）:15-20.

［5］ Thatte A, Salant R F. Elastohydrodynamic analysis of elastomeric hydraulic rod seal during fully transient operation［J］. ASME Journal of Tribology, 2009,131(3): 031501-1-031501-10.

［6］ 钟亮,赵俊利,王志强,等.气动式输弹机密封装置的密封性能分析［J］.兵器材料科学与工程,2014（1）: 77-81.

［7］ 李振环,李德刚. 聚四氟乙烯包复橡胶O形圈制造技术［J］. 流体机械 , 1997, 25(10): 44-46.

［8］ 韩传军,张杰.往复密封用X形圈的优化设计及有限元分析［J］.液压与气动 ,2012（10）:76-79.

［9］ 韩传军,张杰,黄岗,等.往复密封中星型密封圈的密封性能分析［J］. 润滑与密封 , 2012,37(9): 28-32, 36.

［10］ 杨波,王锦江,张永明. 星形圈水下往复动密封分析［J］. 液压与气动 , 2015（8）:73-74,25.

［11］ 韩传军,张瀚,张杰. 星形橡胶密封圈的密封特性分析及截面改进［J］. 机械设计与研究 , 2015（4）:90-94.

［12］ 汤斌,薛璞,王华. 车氏密封在水下电机密封装置中的有限元分析［J］. 机械研究与应用 , 2012（2）:76-77, 80.

［13］ 胡琦.液压伺服作动器O形密封圈实验研究与有限元分析［D］.哈尔滨：哈尔滨工业大学, 2011.