订单陆续到达下虚拟单元重调度驱动决策
2018-01-25韩文民李正义翁红兵蒋家尚
韩文民,朱 弢,李正义,翁红兵,蒋家尚
(1.江苏科技大学经济管理学院,江苏 镇江 212003;2.沪东中华造船集团有限公司,上海 200129;3.江苏科技大学数理学院,江苏 镇江 212003)
1 引言
虚拟单元制造系统(下文简称虚拟单元)是单元生产方式新的发展,是一种先进的生产组织形式。虚拟单元不需要对设备的物理位置进行重新安排,在逻辑上对资源进行聚类成组形成单元,大大减少了设备的移动成本和调整时间[1]。虚拟单元结合了单元式布局和工艺化布局的优点,能够充分挖掘制造系统中设备资源的能力,可以很好地适应当前多品种小批量的生产要求[2]。虚拟单元可以更为灵活地进行调整和变动,但同时必然会为其调度过程增加复杂度。
制造业环境复杂多变,存在着大量不确定的因素,各种类型的干扰事件随时会出现,如工件优先级变动[3]、机器故障[4]等。为了对出现的扰动作出响应,以适应当前的生产状态,需要对原有的生产调度计划进行重新调整。
先前的学者已经对单机、平行机、流水车间、加工车间等不同生产制造方式下的重调度问题进行了大量的研究。刘乐[5]研究了一批新工件到达干扰条件下的单机重调度,在保证最小化最大延迟时间的同时,限制了干扰对初始最优排序工件序位的影响量。Yin Yunqiang等[6]面对平行机发生机器加工中断,在不过多破坏原调度的基础上,提出了解决受影响工件的重调度模型,并分析了模型求解算法。Wang Kai等[7]提出了一个新的两阶段仿真模型,用于评估加工时间不确定的混合流水车间重调度候选方案的性能。薄洪光等[8]分析了在工件变更扰动情况下如何运用干扰管理理论来应对,解决了原调度受干扰事件影响而出现与实际偏离的问题。Lu等[9]分析了制造车间重调度过程中不同分派规则的效率与性能。Elnaz等[10]建立了动态环境下的虚拟单元调度数学模型,综合考虑了需求变化、机器加工能力以及人员分配等多个因素。
目前国内外关于重调度问题的研究,主要集中在重调度方法的优化和重调度性能的评价这两个方面[11]。大多数研究的重点是在确定触发重调度的前提下,通过调度模型的优化与算法的改进,使重调度方案具有更好的性能,且更符合生产实际情况。而针对重调度的驱动决策,即是否需要进行重调度以及何时进行重调度的问题,给予的关注相对较少。
Adibi等[12]在研究柔性流水作业动态调度问题时,将新工件到达以及机器故障选取为进行重调度的时刻。Wortmann[13]根据基于事件的驱动方式,通过评估重调度的可行性,以选择合适的重调度方法。张洁等[14]考虑到了工件在生产会发生加工工时偏差的问题,设计了基于交货期偏差容忍度的混合流水车间滚动调度策略。汪双喜等[15]采用周期性再调度的方式,以应对柔性作业车间中工件随机到达的情况,并对周期驱动中不同长度的调度周期对生产的影响进行了研究。Qiao Fei等[16]面向半导体生产线的不确定性问题,建立了一种重调度模糊PETRI网推理模型。刘明周等[17]针对制造车间机器故障和工件加工时间延长,基于损益云模型判断选择合适的重调度策略。Iraj[18]等根据虚拟单元生产系统中产品组合与部件需求变化,将生产计划分为多个阶段,基于模糊目标规划方法,建立了多周期调度模型。
现有研究中,常用的重调度驱动有周期性驱动、事件型驱动以及混合驱动。对重调度驱动的分析与讨论,大多是针对特定干扰事件进行驱动方法的应用,对重调度驱动方法本身进行改善的较少。同时,现有的重调度驱动也存在对生产系统产生负面影响之处。周期驱动应对突发事件干扰能力不强[15];事件驱动会对系统稳定性造成较大程度的影响[14];混合驱动大多为单一驱动方式的简单叠加,反而会导致调动更加地频繁[12]。
新订单到达是虚拟单元最常见的干扰事件之一。在实际的生产中,现有的加工任务会在加工开始之前已按某一调度方案安排好,然而在加工开始后,新订单会在某个不确定的时刻到达。若得不到合理的调度安排,会使新到订单等待时间过长,生产设备利用率低下,因此需要考虑重新进行新到达任务与原有未完成任务的时间安排[5]。新订单的到达不是一次性的,而是在时域上陆续到达。在先前研究中,面对陆续到达的订单,学者大都在新订单到达时立即构建新的优化调度,以保证新订单到达后及时融入调度之中。这种方式下,生产调度计划不断变动,往往使作业人员无所适从,影响了车间层的控制,降低了生产系统的稳定性,导致了调度的“神经质”现象[19]。生产计划改变过于频繁,严重的将导致生产计划系统的崩溃。
因此,针对订单陆续到达的这一干扰,为了保证虚拟单元重调度兼具适应性和稳定性,本文侧重于执行重调度方案之前的驱动决策,即决定是否以及何时进行重调度。通过对重调度驱动进行决策,以减少重调度对生产计划产生的震荡。为了合理解决是否进行重调度以及何时进行重调度的问题,本文首先建立了一个新的虚拟单元重调度模型作为驱动决策的基础,该模型在约束条件中考虑了调度方案的继承性,对虚拟单元中物流路线庞杂的问题也进行了优化。基于此模型,本文提出了一种新的基于损益的虚拟单元周期-事件混合重调度驱动决策方法,以解决单纯进行周期或事件驱动以及两者简单叠加驱动的不足。该方法通过衡量重调度方案的损失与收益,对每个重调度时刻进行选择,从而实现对重调度频率的优化。
2 虚拟单元重调度模型及算法
本文所提出的重调度驱动决策方法的流程如图1所示。由于本文从重调度方案损失和收益的角度判断是否进行重调度,需要预先制定重调度方案作为驱动决策的基础。因此,本节将结合虚拟单元特性建立重调度优化模型。图中虚线表示生成的调度方案并不一定是最终会实际执行的方案,需要根据驱动决策的结果进行判断。

图1 重调度驱动决策方法
2.1 多目标优化模型
在新订单陆续到达的环境下,订单不断累积等待加工,系统的完工时间会因为加工任务总数的增加而被延长。因此,本文将最大完工时间作为重调度优化目标之一,最小化新订单对完工时间产生的扰动。同时,完工时间越小,机器的等待时间也就越小,系统的设备利用率就越高。
虚拟单元是由物流连接而成的,单元内的设备并不像传统单元一样聚集在一起,前后道工序所需的机器并不相互靠近放置同一区域。在整个加工生产过程中,设备之间的距离不可被忽略不计。每个工件可以有多条不同的加工路径,而且每道工序的加工有多台相同或相似的设备可供选择。不同的调度安排,会导致工件运输路线也不一样。虚拟单元中物流路线十分庞杂,频繁的重调度会使运输路线更为紊乱。本文将工件总运输距离也作为模型的目标之一,以保证生产系统物流的优化。
与一般静态调度不同的是,在重调度开始时刻,并不是所有设备和工件都是处在闲置状态,部分工序正在对应的机器上进行加工。在加工任务具有不可中断性的前提下,重调度不能打断当前正在工作的机器设备,即机器必须完成当前正在进行的任务后,方可安排其他加工任务;工件必须等待当前正在加工的工序完成后,方可进行下一道工序的生产。此外,对于重调度时刻所有等待加工的工件,无论到达时间先后,不考虑其他因素,相互之间没有优先级与紧迫程度的区分;工件的工序必须按照工艺要求的先后顺序进行加工;在某一时刻,每个工件最多只能在一台设备上加工,相应地,每台设备最多只能在加工一个工件;不考虑批量分割。
符号说明:
j表示工件的序号(j=1,2,3,...,J),J为本次重调度中工件的总数;
i表示各工件的工序序号(i=1,2,3,...,Ij),Ij为工件j的工序数;
m、k为设备序号(m,k=1,2,3,...,M),M为虚拟单元系统内设备总台数;
h表示某一设备上所有加工任务的顺序号(h=1,2,3,...,Hm),Hm为设备m上的任务总数;
oj,i表示工件j的第i道工序;
pm,h表示设备m上加工的第h个任务;
参数:
Tj,i,m——表示工件j的第i道工序在设备m上的单位加工时间;
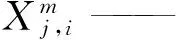
Bj——表示工件j的加工批量;
Dm,k——表示工件从设备m到设备k之间的运输距离;
N——表示一个非常大的正数;
ω1、ω2——分别表示目标函数中完工时间与总运输距离的权重;
决策变量:
Cmax——表示系统的完工时间,即最后一个工件加工完成的时间;
Yj,i,m——当工序oj,i被分配至设备m上加工时为1,否则为0;
Zj,i,m,h——当工序oj,i被分配在设备m上第h个加工时为1,否则为0;
STj,i——表示工序oj,i的开始加工时间;
SMm,h——表示任务pm,h的开始时间。
虚拟单元重调度数学模型建立如下。
目标函数:
(1)
约束条件:
Cmax≥STj,i+Bj·Tj,i,m∀i,j,m
(2)
STj,i+Bj·Tj,i≤STj,i+1∀i,j,m
(3)
SMm,h≥SMm,h-1+Zj,i,m,h-1·Tj,i·Bj∀i,j,m,h
(4)
STj,i+N·(1-Zj,i,m,h)≥SMm,h∀i,j,m,h
(5)
SMm,h+N·(1-Zj,i,m,h)≥STj,i∀i,j,m,h
(6)
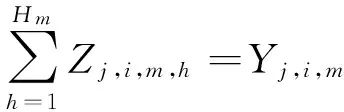
(7)
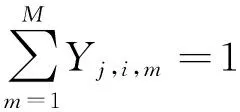
(8)
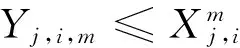
(9)
Cmax≥0,STj,i≥0,SMm,h≥0
(10)
Yj,i,m∈{0,1},Zj,i,m,h∈{0,1}
(11)
模型的目标函数为最大完工时间和总运输距离加权最小。式(1)中,第一项表示加权后的最大完工时间指标,第二项表示加权后的所有工件总运输距离指标。
在约束条件中,式(2)表示最大完工时间变量的取值范围约束,该变量值必须大于或等于所有工序的最终完成时间;式(3)确保同一工件各道工序的前后顺序满足加工工艺约束,每个工件的前道工序加工完成后才能开始后道工序的加工;式(4)为每台设备上的加工任务继承性约束,每个任务必须等该设备上先前的任务加工完成后才可进行,若为本次调度期内机器上的第一个加工任务,则需等待上一调度期遗留的、当前仍正处于加工状态的工件生产完成;式(5)和(6)表示若工件j的第i道工序被分配在设备m上第h个加工时,oj,i与pm,h开始时间相等,用于关联时间层面上工件的先后安排与设备的资源分配;式(7)保证每台设备每个时刻最多只能被安排对一道工序进行加工;式(8)保证每个工件的每道工序不可能被分配到超过一台设备上进行生产;式(9)保证每道工序在满足其工艺需求的设备集中选择机器;式(10)表明决策变量的非负性;式(11)表明决策变量为二进制变量,即对该变量的赋值只能为0或者为1。
2.2 混合离散粒子群算法
为了保证调度结果的方案的最优化,本文采用一种结合粒子群算法和遗传算法的混合离散粒子群算法,来求解上文中所建立的虚拟单元重调度模型。该混合算法将遗传算法的部分操作加入到粒子的状态更新中,指导整个群体的进化过程。粒子群算法所需要的控制参数比较少,而且可以很快收敛,同时具有很好的鲁棒性,被普遍应用于各种类型的优化问题[20]。与之相比,遗传算法尽管局部搜索效率比较低,但它的全局搜索能力相对粒子群更好。利用粒子群算法与遗传算法的有机组合,能够充分利用各算法的优势,避免使用单一算法的不足。该混合算法的原理与传统连续型粒子群算法类似,主要的改进在其中于遗传粒子的编码以及遗传粒子更新的方式。
粒子编码:虚拟单元内的机器设备“一专多能”,工件具有多条工艺路径,在原调度与重调度方案中,同一工件可以被分配到不同机器上加工。粒子的编码,不仅要能体现工件加工顺序信息,也要包含工件对机器选择的信息。
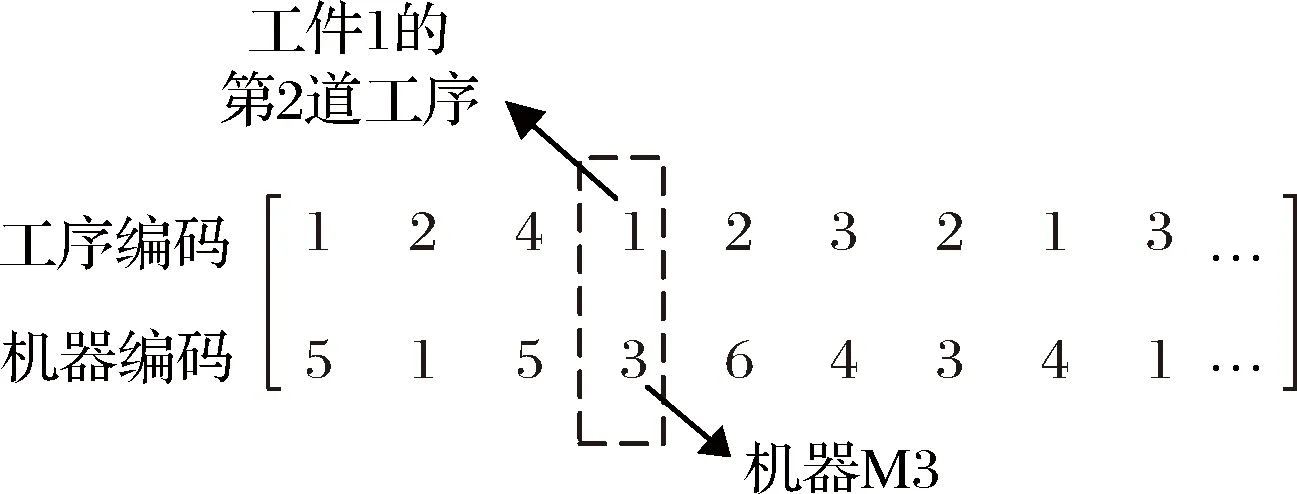
图2 粒子编码示意图
在算法开始前,需进行初始化处理,将种群信息设置为某一状态。在保证编码合法性的前提条件下,将随机地生成的初始位置与初始速度赋予给粒子。求出各个粒子当前位置所对应的目标函数值,并找出当前种群最优解。由于尚未进行迭代,各粒子初始位置对应的目标函数值即为最优,则设为当前的历史最优解。
粒子更新:粒子从个体及邻域获得更新信息的方法并不是单一的,可采用多种形式的,遗传算法的交叉操作[21]也可以成为是粒子改变速度和位置的一种方式,而变异操作可以看作是粒子的随机搜索过程。粒子通过模仿染色体的交叉方法,实现速度和位置的更新。粒子的速度与当前其个体最优解以及群体最优解分别进行交叉来得到改进,粒子的位置更新则由粒子的当前位置与当前速度进行交叉来获得。引入遗传操作后,粒子的速度-位置更新公式表示形式如下:
Vi(n+1)=Vi(n)⊗Pibest⊗Pgbest
(12)
Xi(n+1)=Vi(n+1)⊗Xi(n)
(13)
其中n表示迭代次数,Vi表示粒子速度,Xi表示粒子位置,Pibest表示当前个体最优位置,Pgbest表示当前群体最优位置。
当某个粒子经过连续多次迭代,可能会出现自身信息与之前相比变化的差异幅度很小,那么说明这个粒子可能被限制在当前所在区域,陷入了局部最优的状况。需引入新的信息,促使粒子跳到解空间中的其他区域,继续进行移动并搜寻。此时,对粒子个体极值进行变异的处理,具体处理方式的公式表示如下:
Pibest(n+1)=mutation(Pibest(n))
(14)
该混合离散粒子群算法流程如图3:
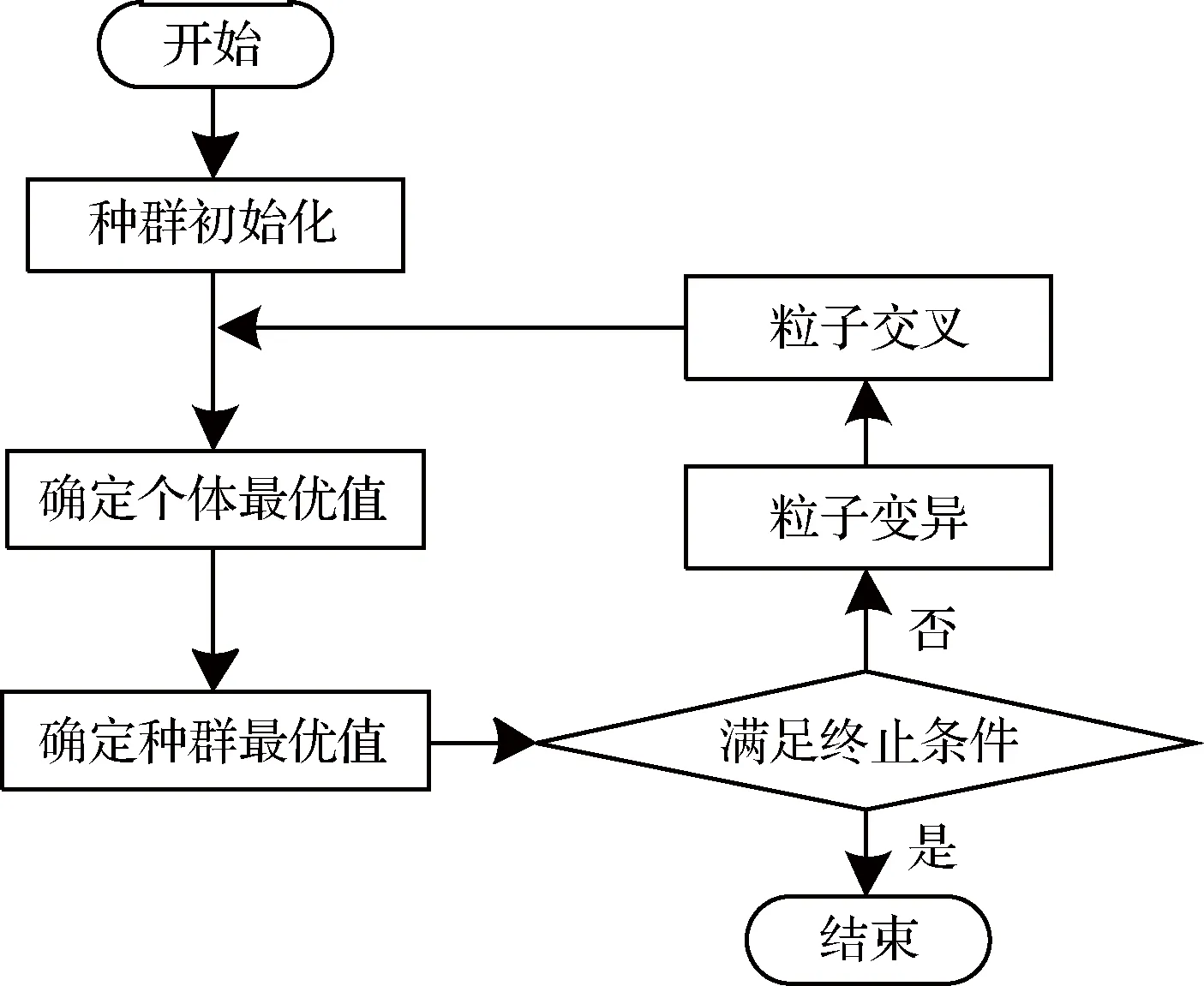
图3 混合离散粒子群算法流程
3 重调度驱动决策
3.1 重调度决策时刻
新订单陆续到达的环境下,调度任务集是不断变化的。运用滚动时域法中的滚动窗口技术,可以将新订单陆续到达的动态过程进行分解,将动态调度分成多个连续有重叠的静态区间,把不确定性调度问题转变成一系列确定的调度问题。滚动窗口与任务集合的关系如图4所示,在重调度时刻,已完工的任务将被从调度窗口中移除,同时,新到的任务将被添加到窗口中。随着窗口的前移,如此反复直到所有工件都加工完成,以此应对新订单陆续到达干扰下,加工任务集合的不确定性问题。
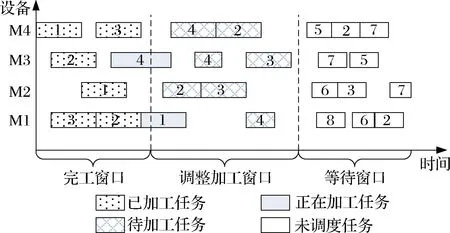
图4 基于滚动窗口的任务集划分
从单个订单层面看,新订单到达属于显性干扰事件,可采用事件驱动重调度。将新订单到达作为关键事件,该关键事件一旦发生即主动触发一次重调度。采用事件驱动,系统能够及时和灵活地应对新到订单。
周期驱动在一定程度上也可以应对新订单到达对虚拟单元的扰动。实际生产中,订单由计划层不断下发,制造系统会陆续地接受到新的订单任务。采用周期驱动,每间隔固定时段将新到达的订单纳入调度窗口,对所有待加工订单进行重调度,使系统更为平稳。
从周期与事件混合策略生成的重调度时刻集合中进行重调度驱动决策,可以结合两者优势,保证用于决策的时刻更为有效。因此将混合策略生成的重调度时刻集合作为驱动决策与筛选的来源。
然而由于订单到达时间的不确定性,重调度周期的设置是关键问题。考虑到在单位时间内,到达的新订单数量越多,对系统的扰动越大,重调度频率也应相应加大。因此,重调度周期与新订单到达速率密切相关。
新订单的到达是不可确知的,但是可视为服从某种概率分布。普遍认为工件到达时间间隔服从参数为λ的指数分布。参数λ为工件的平均到达率,一般地,该参数可用如下公式表示[22]:
(15)
上式中,η表示所有设备的总体利用率,M表示设备的总数,μt表示每道工序的平均加工时间,μp表示每个工件的平均所含工序数。
由此,根据周期驱动方式可以得到一系列重调度点T1={tn|tn=t0+n·ΔT};根据事件驱动方式得到另一系列重调度点T2={tn|tn=t0+∑τn}。则T3={tn|tn∈T1∪T2} 即为新的重调度决策时刻集合。
3.2 重调度收益
在虚拟单元制造系统中,当单元内的加工任务完成,机器设备就可以从该逻辑单元中释放,与其他设备组成新的虚拟单元进行其他生产任务。完工时间越小,意味着机器能够及早被释放。系统的产出与生产时间是正相关的,借用经济学中机会成本的概念,完工时间提前,用于其他生产任务的时间增加,为系统带来额外的潜在收益。
当新订单到达系统后,若不进行重新安排,系统原有订单按原调度计划继续生产,新订单进行等待。若不考虑后续订单的到达的影响,新订单的加工在原有已调度任务加工完成后进行。单独完成新订单所需的时间记为TCN。
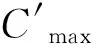
重调度后,系统生产结束时间的提前量:
(16)
则重调度带来的额外收益为:
(17)
式中,θ为延期惩罚系数。
3.3 重调度损失
重调度可以使某个调度目标得以优化,但与此同时,也会引起生产资源的重新配置,必然会带来额外的成本。调度方案的改变,给生产系统带来或大或小的损失。在重调度后,由于新到订单的插入生产,导致部分原有订单的生产计划受到影响,工序的加工安排被延后。而由于这样的变动,相关配套件的需求计划以及生产物流的规划都随之发生改变,物料供给和运输时间安排都需要做出相应的调整,导致库存和运输成本的增加。
本文用重调度前后工序开始时间的变动来反映重调度带来额外的损失,以所有工序被推迟的时间总和来衡量成本的大小。
原调度中所有工件的工序集合记为UO,重调度所涉及的工序集合记为UR。重调度时,原有的且已加工完成的工序不参与重调度,后续到达的新订单的工序则会被添加至调度窗口;则受重调度影响的工序集合为UE=UO∩UR。
若工序oj.i在集合UE之中,用STj,i和ST'j,i分别其表示在原调度和重调度方案中工序的加工开始时间。
工件j的工序oj,i在新旧调度方案中的开始加工时间偏差为:
SCj,i=ST'j,i-STj,i
若ST'j,i-STj,i<0,令SCj,i=0
则重调度引起的额外损失为:
(18)
式中,δji为工件j第i道工序oj,i的加工开始时间变动惩罚系数。
3.4 决策方法
若混合驱动仅仅将周期驱动与事件驱动产生的重调度时刻相叠加,这将导致重调度次数过多。上文中,T1和T2是按照各自的驱动方式独立生成的,当它们加合在一起后,数量较多,而且很有可能在短时间内,连续触发重调度,出现重调度点相邻过近或者分布过于紧密的问题。另外,从成本角度考虑,并不是每一个重调度点都是恰当的重调度时刻。因而,需要对重调度时刻进行判断和决策。
本文将从重调度带来损失与收益的角度,提出混合驱动下的重调度驱动决策。该混合驱动决策方法,不是在生产加工开始前的一次性的全局判断,而是在每个重调度点,基于当前实际工况,进行一次在线决策。
每当新订单到达,或是周期时刻来临时,根据上文中所提的虚拟单元重调度模型,生成重调度预实施方案。计算出重调度方案的额外收益RDC与额外损失LSC的值。判断当执行预实施方案时,重调度过程中带来的损失是否能够弥补其能获得的收益。
若RDC≤LSC,表明产生的新调度方案与原调度方案相比,获得的预期收益不能够弥补或仅仅能够弥补调整带来的损失,此次重调度不能在成本层面使系统得到优化,此时刻没有更新调度方案的必要,取消此重调度点,继续执行原调度方案至下一个重调度时刻。
若RDC>LSC,则表明重新调度带来收益相对于其造成的损失更大,此时刻按照新方案执行重调度。具体的重调度驱动详细流程如图5所示。
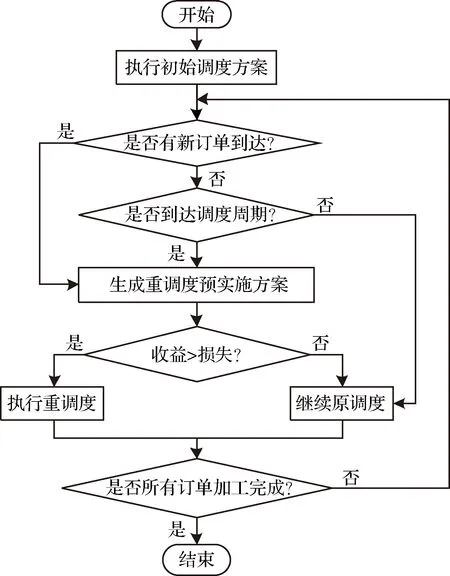
图5 基于损益的重调度流程图
4 实例分析
船舶建造是虚拟单元的典型代表,本文选取了H船厂中的分段建造车间为对象,应用实例数据,研究所提出重调度驱动决策方法的有效性和可行性。
4.1 基本数据
本案例中,根据加工任务的相似性所形成虚拟单元制造系统涉及5个工作区,每个工作区内的设备类型不同,每种类型的设备有多台,设备的基本信息如表1所示;设备间运输距离信息如表2所示。
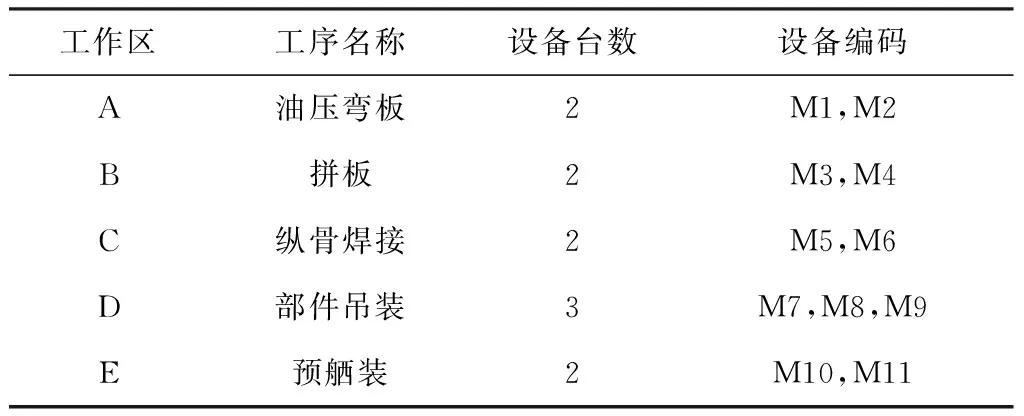
表1 设备信息
在正式生产开始之前,已有部分订单到达生产系统,订单信息如表3所示。
在开始加工后,新订单将会在不确定的时刻,陆续到达系统。为了体现订单到达的随机性,本案例中新订单的到达时间,将通过模拟获得。根据生产车间的历史数据,设备总体利用率η=68.6%,设备总数M=11,工序平均加工时间μt=25.9h,工件平均工序数μp=4.3。由式(15)计算可得新工件的平均到达率λ=0.0679,通过随机生成一组服从参数为λ的指数分布的数列,可得到的新订单的到达时间间隔,通过累计时间差可得到各订单实际的到达时间。为了简化计算便于说明问题,对到达时间进行了取整。新订单的信息如表4所示,但实际上,新订单的各项属性以及其到达时间在其到达之前未知。
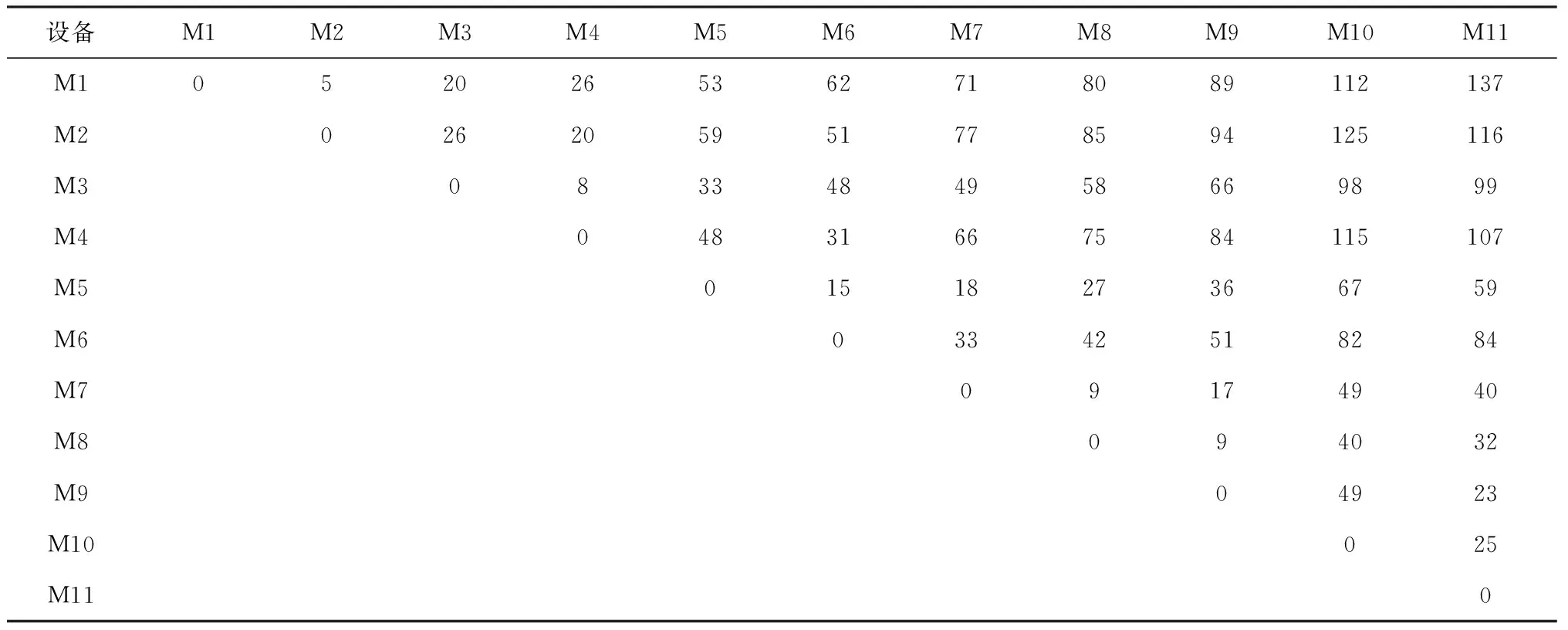
表2 设备间运输距离(单位:米)

表3 订单加工任务信息

表4 新到达订单信息
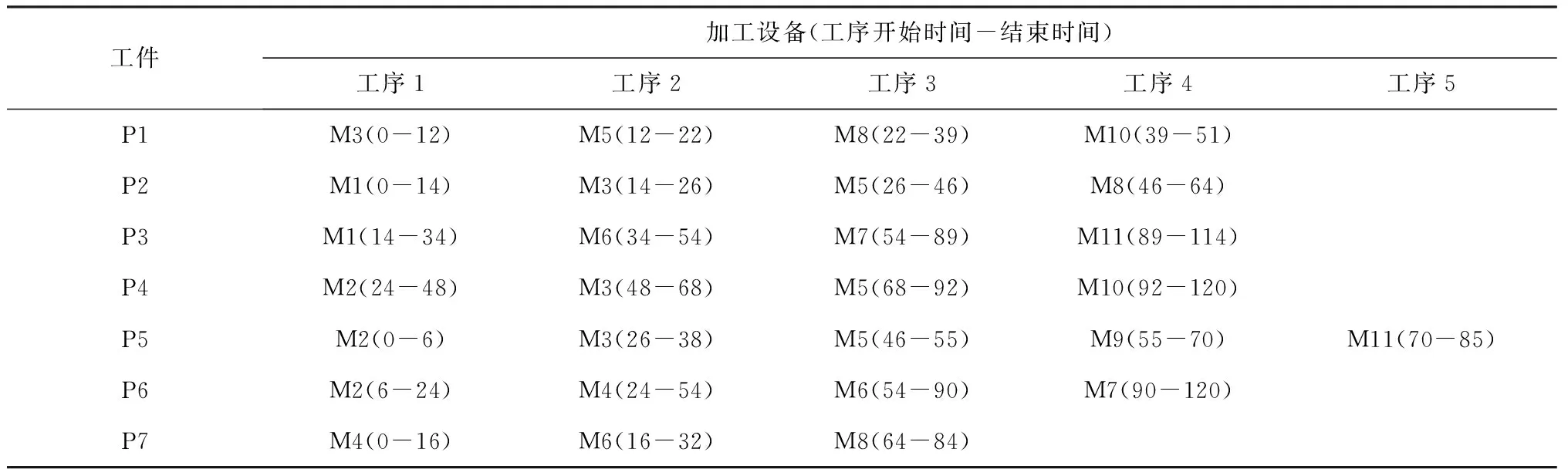
表5 初始调度计划时间安排
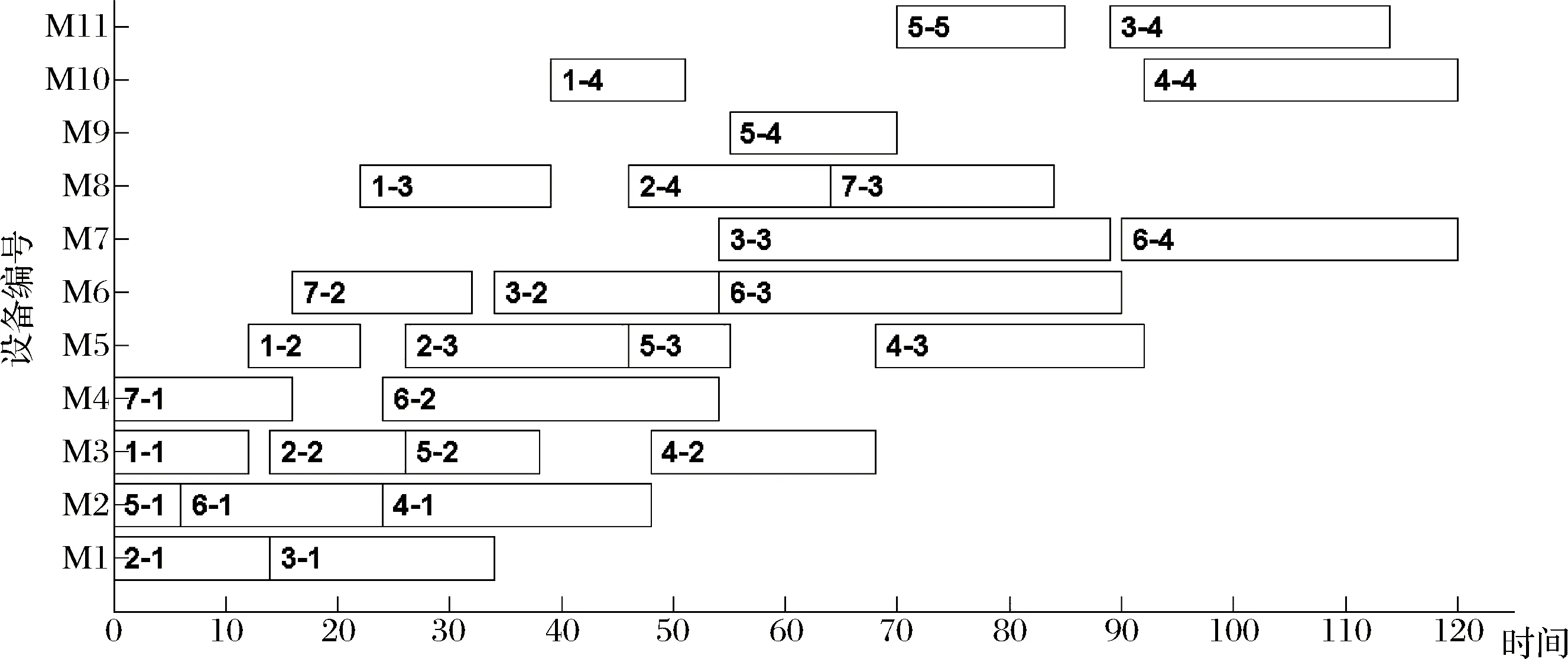
图6 初始调度方案甘特图
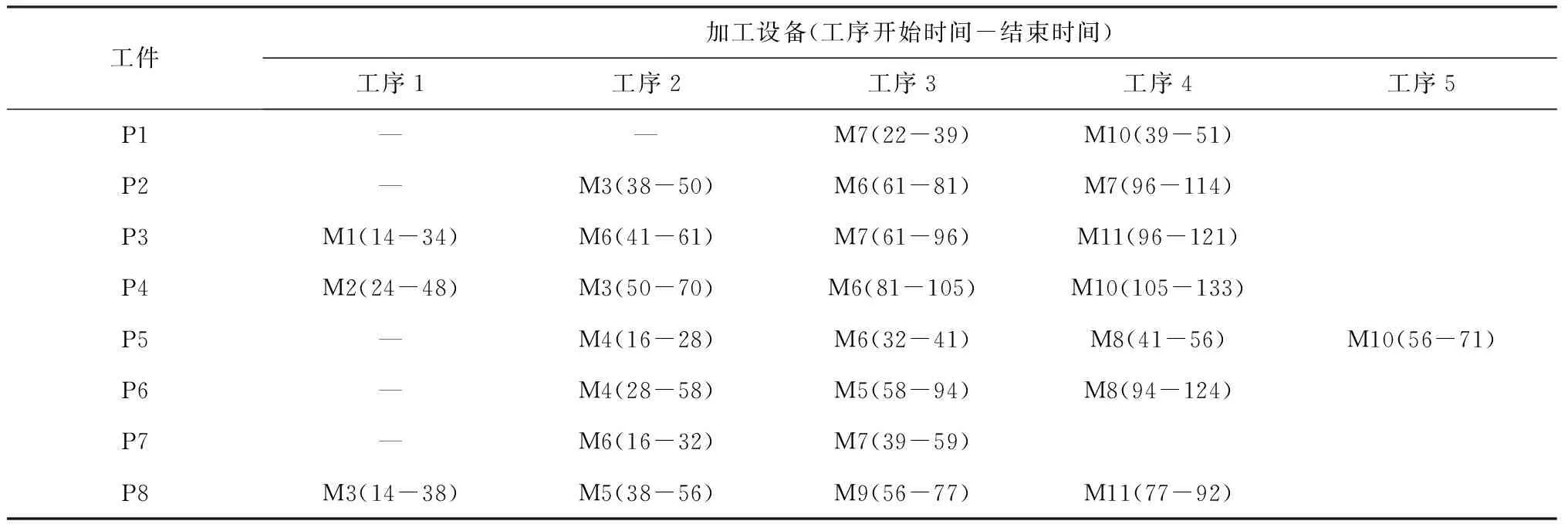
工件加工设备(工序开始时间-结束时间)工序1工序2工序3工序4工序5P1——M7(22-39)M10(39-51)P2—M3(38-50)M6(61-81)M7(96-114)P3M1(14-34)M6(41-61)M7(61-96)M11(96-121)P4M2(24-48)M3(50-70)M6(81-105)M10(105-133)P5—M4(16-28)M6(32-41)M8(41-56)M10(56-71)P6—M4(28-58)M5(58-94)M8(94-124)P7—M6(16-32)M7(39-59)P8M3(14-38)M5(38-56)M9(56-77)M11(77-92)
4.2 结果分析
根据所给出的算例基本信息,对于本文提出的虚拟单元重调度模型,使用matlab7.0软件进行计算;混合粒子群算法迭代次数为200,交叉率为0.8,变异率为0.6;设置重调度周期ΔT=25,取δji=0.4,θ=0.6。
下面将结合案例,详细阐述本文所提出的重调度驱动方式,说明其具体步骤。
在初始0时刻,将虚拟单元内原有订单调度安排完毕,初始调度方案如表5所示,相应甘特图如图6所示。
当t=14时,新订单8到达。此时,工序o1,1、o2,1、o5,1已加工完成,工序o1,2、o6,1、o7,1正在加工。若此时将剩余的未加工工序与新订单进行重调度,求解重调度模型,生成的新的调度计划如表6所示。
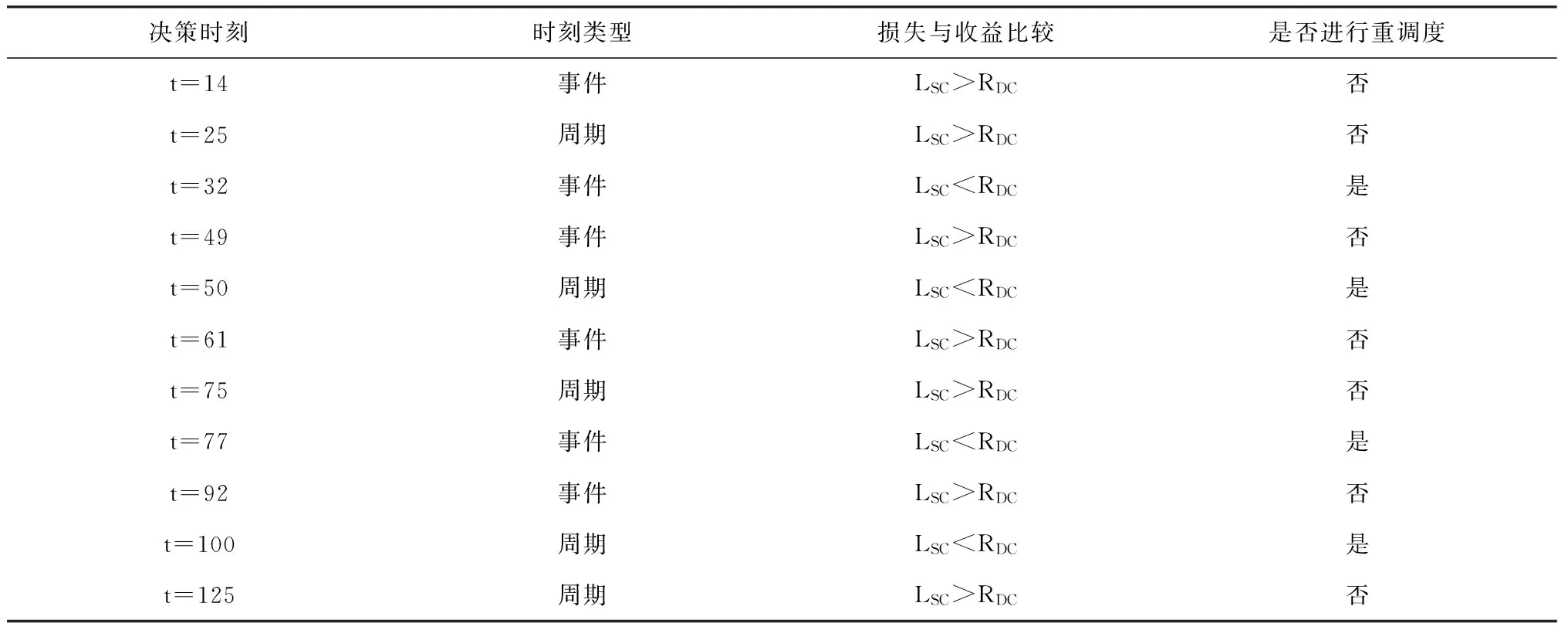
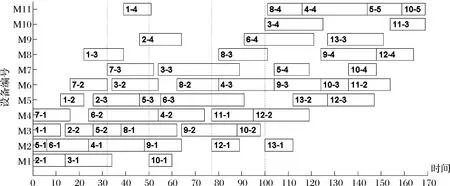
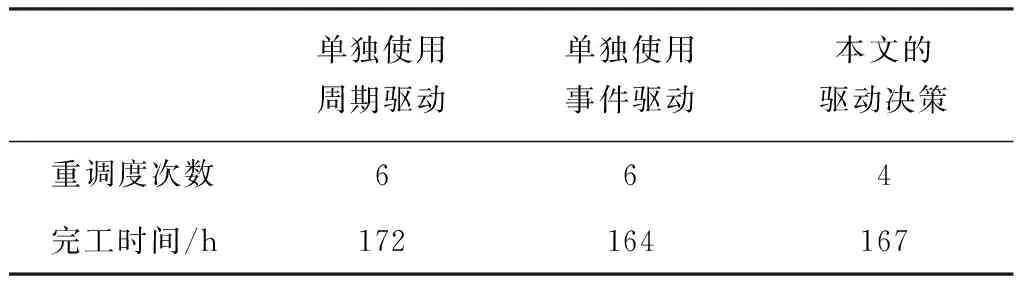
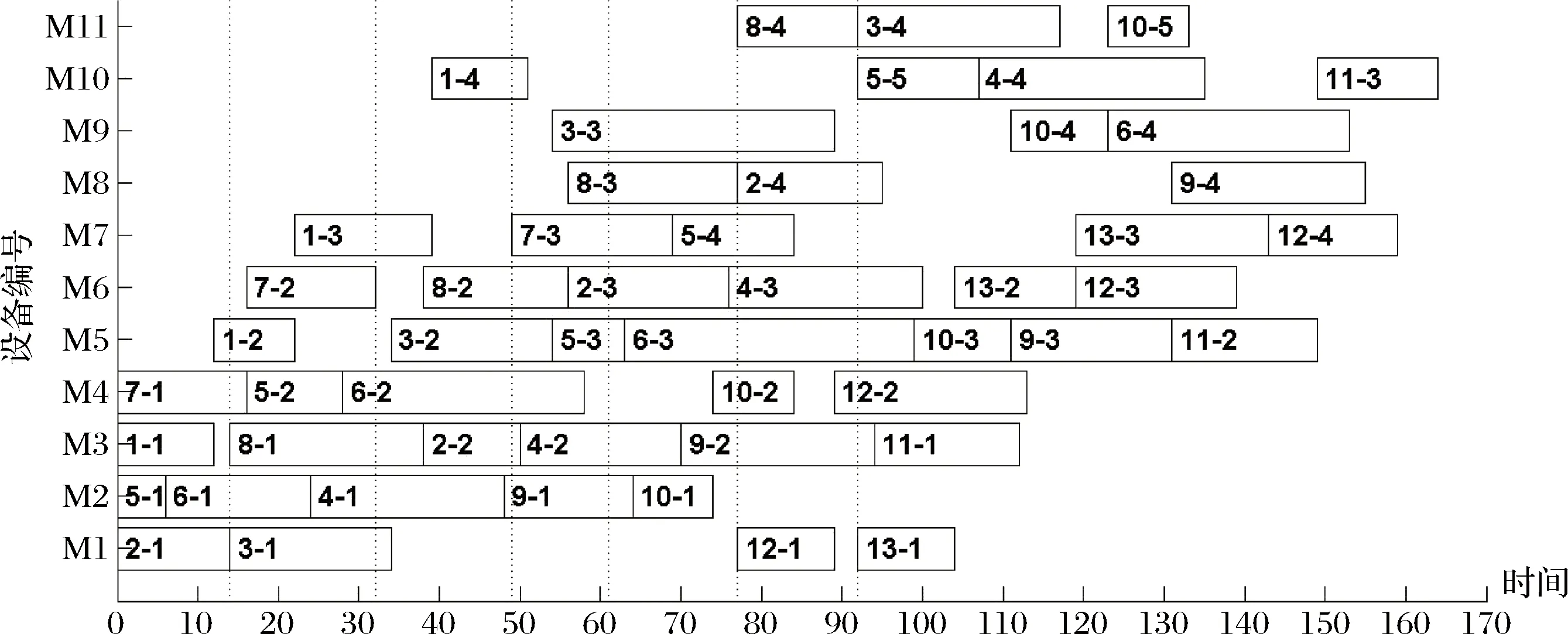
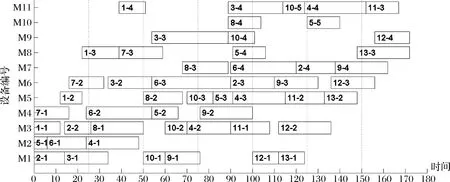
在重调度方案中,由于订单8的加入,原工序集中共有9道工序的开始加工时间被推迟,工序开始加工时间偏差总和为170h;而重调度预计完工时间提前量为65h。假设实施重调度,根据式(17)和(18)计算,得LSC=68,RDC=39,RDC t=25时,此时到达第一次周期性重调度时刻。原有工序集合中,有16个工序尚未加工,新订单8处于等待状态。首先生成预调度方案如表7,计算得LSC=45.2,RDC=39,此时刻重调度损失较上一时刻的小,但仍不是最佳调度时刻。 新订单9在t=32时到来,表8为此次重调度方案,再次进行重调度收益与损失的比较,LSC=50.4,RDC=81.6,RDC-LSC>0,通过判定,生产系统将会按照表8的方案进行新的调度。 同样地,在接下来的每一个由周期驱动或事件驱动生成的重调度点,均生成一重调度方案,然后通过对比LSC和RDC,决定是删除该重调度点,或是立即执行重调度方案。案例中各重调度点的决策情况如表9。 当所有订单加工完成,在改进的混合驱动方式下,调度甘特图最终如图7所示,图中虚线表示该时刻进行了重调度。 表7 重调度方案(t=25时刻) 表8 重调度方案(t=32时刻) 表9 重调度判定 图7 混合驱动决策后的调度甘特图 为表明本文所提出的重调度驱动决策方法的有效性,将其与使用周期驱动以及事件驱动下的调度安排进行对比。图8为单独使用事件驱动下的调度甘特图,图9为单独使用周期驱动下的调度甘特图。 三种驱动方式评价对比,如表10所示。由于周期驱动不能及时响应动态变化,所需完工时间最长,且存在明显的不必要重调度;事件驱动可以使得调度的完工时间目标更优,但需要的重新调度次数也较多。使用改进的混合驱动方式,调度次数在三种方式中最少,完工时间也比单独使用周期驱动要好。尽管完工时间并不是最优结果,但是减少了重调度次数,亦即减少了对生产系统的震荡影响,因而也减少了由此带来的一系列损失,而完工时间指标也在可接受范围之内。因此,本文的驱动决策方法对于重调度的优化结果是令人满意的,且更具有实际应用价值。 表10 三种驱动方式结果比较 图8 事件驱动下的调度甘特图 图9 周期驱动下的调度甘特图 本文研究订单陆续到达环境下虚拟单元的重调度驱动决策问题。根据虚拟单元特性,建立了多目标重调度数学模型,并设计了一种混合了遗传操作的离散粒子群优化算法用于求解;在周期和事件混合驱动下,提出了一种新的重调度决策方法,从时间的角度,衡量重调度的损失和收益,选择合理的重调度决策时间点。实例分析表明,在调度决策目标优化的同时,重调度频次有明显的减少。与单独的周期驱动或事件驱动下的重调度相比,本文提出的混合驱动下的重调度,在调度次数和完工时间上有明显的优势。本文提出的重调度驱动决策方法,加强了生产系统的整体稳定性,能够较好地缓和因频繁重调度而引起的生产系统震荡,可以作为制定重调度的触发开启时间的依据。 本文提出的订单陆续到达下虚拟单元重调度驱动决策,是作为重调度的基础与前提。在解决了是否进行重调度的问题之后,后续的研究工作可关注重调度方法的进一步改进。为了避免重调度后虚拟单元产生资源配置混乱的现象,考虑到计划冻结技术能够保持计划的相对稳定,可将其引入重调度之中,在进行驱动决策后,保持部分原有任务的安排不发生改变,使新调度方案能够更好地衔接原方案,更好地提高动态调度的稳定性。同时,重调度方法大多基于工件一旦在机器上加工就无法中断的假设,可进一步研究订单插入条件下允许加工中断的调度模型,使重调度方案更适合动态生产环境的实际情况。 [1] Tambuskar D, Narkhede B, Mahapatra S. A novel algorithm for virtual cellular manufacturing considering real life production factors[J]. International Journal of Services&Operations Management, 2015, 20(2):246. [2] Ghahve J. Scheduling of virtual manufacturing cells with outsourcing allowed[J]. International Journal of Computer Integrated Manufacturing, 2014,27(12):1079-1089. [3] 刘锋, 王建军, 饶卫振. 安装时间与次序相关的生产调度干扰管理研究[J]. 中国管理科学,2014,22(1):45-54. [4] 郑睿, 吕文元. 考虑故障停机的生产控制与维修计划联合决策模型[J]. 中国管理科学,2016,24(8):116-122. [5] 刘乐, 周泓. 新工件到达干扰下单机最大延迟时间重调度[J]. 系统工程学报, 2014, 29(4):494-506. [6] Yin Yunqiang, Cheng T, Wang Dujuan. Rescheduling on identical parallel machines with machine disruptions to minimize total completion time[J]. European Journal of Operational Research, 2016, 252(3):737-749. [7] Wang Kai, Choi S H, Qin Hu. An estimation of distribution algorithm for hybrid flow shop scheduling under stochastic processing times[J]. International Journal of Production Research, 2014, 52(24):7360-7376. [8] 薄洪光, 张鑫, 潘裕韬. 混合无等待流水线干扰管理调度方法研究[J]. 运筹与管理,2016,25(3):246-254. [9] Lu M S, Romanowski R. Multicontextual dispatching rules for job shops with dynamic job arrival[J]. The International Journal of Advanced Manufacturing Technology, 2013, 67(1):19-33. [10] Elnaz N, Amin A. Production planning and worker assignment in a dynamic virtual cellular manufacturing system[J]. International Journal of Management Science & Engineering Management, 2013, 7(2):89-95. [11] Ouelhadj D, Petrovic S. A survey of dynamic scheduling in manufacturing systems[J]. Journal of Scheduling, 2009, 12(4):417-431. [12] Adibi M A, Zandieh M, Amiri M. Multi-objective scheduling of dynamic job shop using variable neighborhood search[J]. Expert Systems with Applications, 2010, 37(1):282-287. [13] Wortmann J. Coordination activities of human planners during rescheduling: case analysis and event handling procedure[J]. International Journal of Production Research, 2011, 49(7):2101-2122. [14] 张洁, 秦威, 宋代立. 考虑工时不确定的混合流水车间滚动调度方法[J]. 机械工程学报,2015,51(11):99-108. [15] 汪双喜, 张超勇, 刘琼,等. 不同再调度周期下的柔性作业车间动态调度[J]. 计算机集成制造系统, 2014, 20(10):2470-2478. [16] Qiao Fei, Wu Qijin, Li Li, et al. A fuzzy Petri net-based reasoning method for rescheduling[J]. Transactions of the Institute of Measurement & Control, 2009, 31(5):435-455. [17] 刘明周, 张玺, 张铭鑫,等. 基于损益云模型的制造车间重调度决策方法[J]. 控制与决策,2014,29(8):1458-1464. [18] Mahdavi I, Amin A, Mohammad M P, et al. Multi-objective cell formation and production planning in dynamic virtual cellular manufacturing systems[J]. International Journal of Production Research, 2011, 49(21):6517-6537. [19] Rangsaritratsamee R, Ferrell W, Kurz M. Dynamic rescheduling that simultaneously considers efficiency and stability[J]. Computers & Industrial Engineering, 2004, 46(1):1-15. [20] 宋继伟, 唐加福. 基于离散粒子群优化的轧辊热处理调度方法[J]. 管理科学学报, 2010, 13(6):44-53. [21] 李劲, 李洪, 徐丽丽等. 基于改进遗传算法的置换装配线调度问题研究[J]. 中国管理科学,2016,24(12):63-71. [22] Jin L, Zhang Chaoyong, Shao Xinyu, et al. A study on the impact of periodic and event-driven rescheduling on a manufacturing system: An integrated process planning and scheduling case[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 2016,(3):1-15.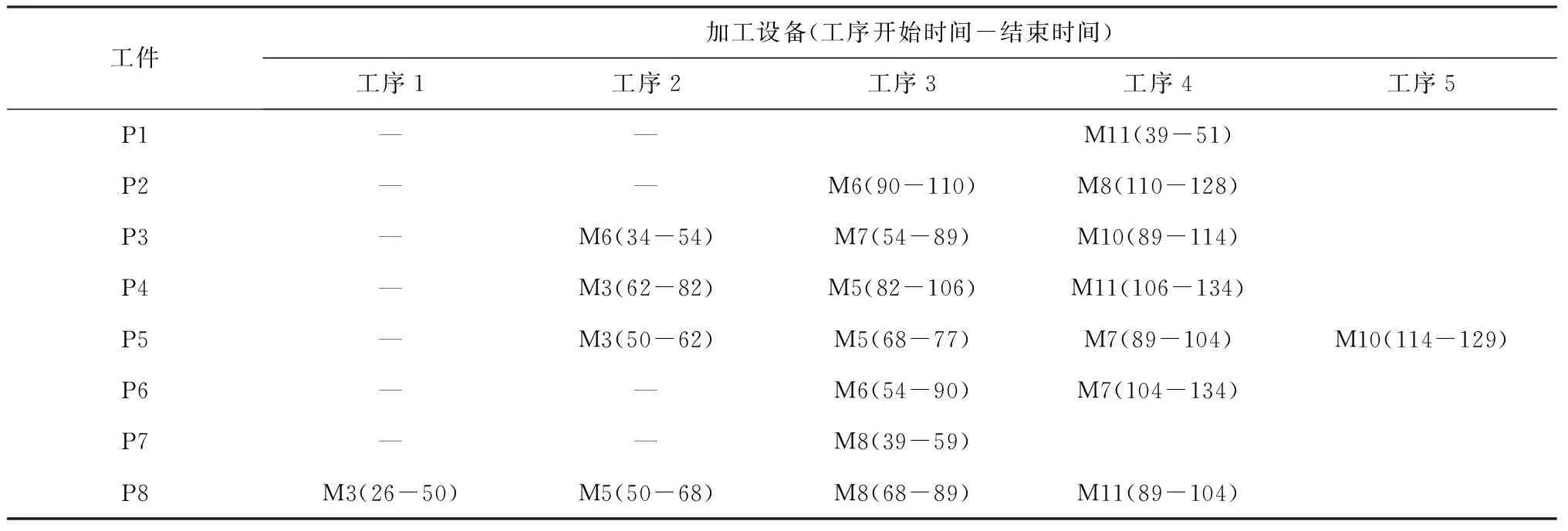

4.3 对比分析
5 结语
