区间值最小二乘核仁解及在供应链合作利益分配中的应用

刘家财，李登峰，胡勋锋

(1.福州大学经济与管理学院工商管理研究院，福建 福州 350116；2.福建农林大学交通与土木工程学院，福建 福州 350002)

1 引言

合作对策的重要解概念有很多，比如，核心、核仁、夏普利值，等。上述解概念均是基于经典合作对策即清晰联盟及清晰效用函数的情形下提出。事实上，任何合作对策都需要考虑环境与条件的不确定性[1-2]、信息的不准确性[3]、局中人目标的多样性与不确定性[1,4]、局中人的主观期望与风险态度[1,5-6]、局中人参与联盟的程度[7]等。换句话说，在现实的经济管理问题中，常存在不确定性及模糊性，导致局中人只能以一定的概率参与联盟或者联盟值(或特征函数)无法用精确实数准确表达。近年来，在合作对策的研究中，常用区间数来表示联盟值(或特征函数)，由此出现了一类支付值为区间数的合作对策，这类合作对策常被简称为区间值合作对策。区间值合作对策是模糊合作对策的一种重要形式。模糊合作对策是经典合作对策的推广，经典合作对策的模糊延拓有三种形式：第一种是联盟模糊而效用清晰的合作对策[7]。第二种是效用模糊而联盟清晰的合作对策[8]。第三种是联盟和效用均模糊的合作对策[9]。早在1974年，Aubin[7]利用美国著名控制论专家L.Zadeh教授提出的模糊集表示局中人参与联盟的程度(或参与率)，提出了模糊联盟的概念，这是合作对策最早涉及模糊不确定性的一类形式。随后，Aubin[10-11]又定义了模糊合作对策的核心，为日后区间值合作对策核心的广泛研究奠定了基础。国外学者Branzei[12-14]、Alparslan[15-17]、Mallozzi[18]等围绕区间值合作对策开展了大量研究。Branzei等[12]针对凸区间值合作对策，提出类似Shapley值的解，为模糊合作对策区间Shapley值的研究奠定了基础。Branzei等[13-14]对区间值合作对策的研究进行了总结与展望，并对区间值合作对策的超可加性、凸性、区间优超核心等进行了定义。Alparslan等[15-17]运用区间数的运算规则对区间值合作对策重新进行定义，对确定条件下即经典合作对策的部分重要解概念及其解法进行拓展，从而发展形成区间值合作对策的解概念及其解法，并对区间值合作对策的核心的一些重要性质进行了探讨。Mallozzi等[18]拓展区间值合作对策模型，提出一种求解区间值合作对策的类似于核心的解概念，并提出一种确保类核心的解非空的均衡性条件。

我国也有诸多学者围绕区间值合作对策做了相关研究，如，李登峰[19]针对联盟值(或特征函数)表示为区间数的多人合作对策，通过研究其合作对策分配值(即解)具有的单调不减性质，提出了相应的简化约束条件，从而利用联盟区间值的左、右端点值，简单、快捷地确定每个局中人分配值(区间值)的左、右端点值，进而确定区间值多人合作对策的区间值分配解，相继提出了区间值合作对策的多种区间值分配解，如，区间值Shapley值，区间值团结(solidarity)值，区间值Banzhaf值，区间值核心分配解，等，并研究了它们的一些重要性质。于晓辉、张强[20]利用区间数运算的性质，将经典Shapley值的三条公理拓广到区间值合作对策中，提出具有区间支付的Shapley函数的具体形式，并且通过论证，证明区间Shapley函数和经典的Shapley函数具有形式上的一致性。高作峰等[21]给出了区间合作对策在增广系统上的定义，并利用相应的公理体系及区间数运算的性质，构造出区间合作对策在增广系统上的区间Shapley值，并对该区间Shapley值的一些重要性质进行探讨。由此可看出，区间值合作对策的研究引起国内外诸多学者的关注。

在经典合作对策中，核心是1953年Gillies[22]引进，后经著名对策论专家Shapley和Shubik[23]发展成为合作对策的解概念。核心是目前使用较多的合作对策的集合解概念，要求满足个体合理性、集体合理性与联盟合理性。核仁是1969年Schmeidler[24]以超量衡量联盟的满意程度，并从最小化联盟的不满意程度出发，提出的合作对策的解概念。核仁后来又进一步发展为多种形式，比如，最小核仁、弱核仁、比例核仁等。尽管在经典合作对策中，核心、核仁等解概念要么包含很多(甚至是无穷多)个元素，要么一个也没有即为空集，我们仍然希望在区间值合作对策中寻找其核心解，给出核心解存在的条件，并讨论其重要性质。本文的主要工作是提出区间值合作对策的最小二乘法预核仁和核仁，并讨论诸如存在性、可加性、匿名性等区间值合作对策解的一些重要性质。与供应链合作利益分配同类研究[25-26]相比较，本文提出的模型与方法考虑了供应链节点企业开展合作时经常出现的模糊不确定性，着重研究联盟的收益表示为区间数时的合作利益分配策略，不仅如此，利用多维线性拓展方法，还可将本文提出的区间值最小二乘核仁解自然拓展至联盟收益表示为三角(梯形)模糊数以及三角(梯形)直觉模糊数的情形。容易证明，利用该方法得到的模糊合作对策的最小二乘核仁解，均具有存在性和唯一性、有效性、匿名性、对称性等合作对策解的良好性质。

2 预备知识

2.1 支付值为区间数的合作对策

2.2 区间值最小二乘法预核仁和核仁及其解概念

(1)

和

(2)

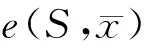
(3)

(4)

和

(5)

即，

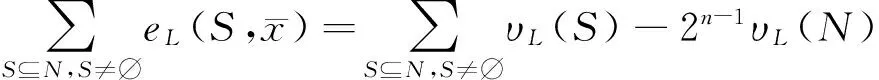
(6)

利用同样的方法，有，

(7)

至此，引理1得证。

根据式(1)、式(4)和式(6)，结合区间值运算规则[27]，式(3)可改写成如下形式：

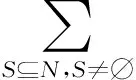
(8)

3基于平方超量的区间值最小二乘法预核仁和核仁的二次规划求解方法

3.1 考虑有效性的区间值最小二乘法预核仁

引理2 区间值最小二乘法预核仁是基于最小化平方超量之和且满足有效性的区间值合作对策的一种分配方案，解二次规划模型(8)便可得区间值最小二乘法预核仁。

证明 根据拉格朗日乘子法，模型(8)可写成如下形式，

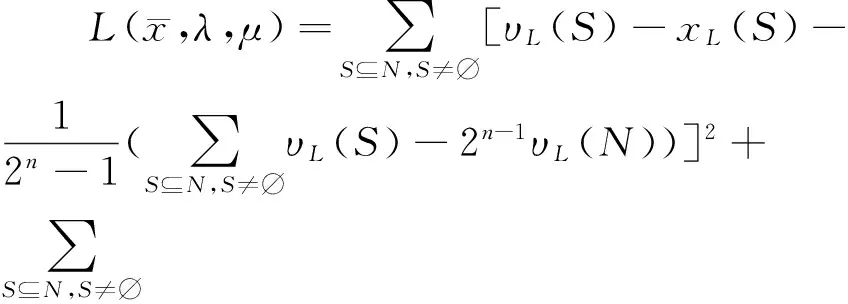
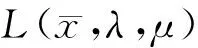
(9)

和

(10)

由于

(11)

根据式(9)和(11)，可得，

又因为

(12)

(13)

其中，s表示联盟S⊆N的个数。

将式(13)代入式(12)，有，

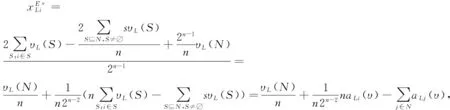
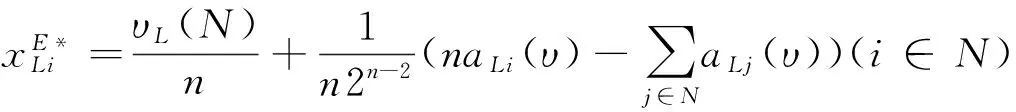
(14)

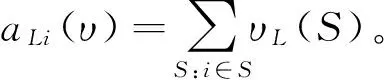
(15)

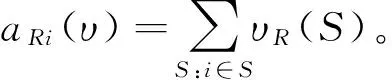
下面，我们讨论区间值合作对策的区间值最小二乘法预核仁的一些重要性质。

证明 根据式(14)和(15)，定理1直接得证。

证明 根据式(14)和(15)，结合区间值运算规则[25]，有，

证明 根据式(14)，有，

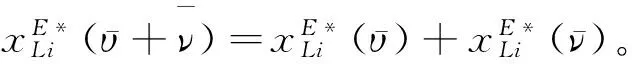
证明 对于局中人i∈N和k∈N(i≠k)，根据式(14)，有，

和

证明 由式(14)和(15)，定理5容易得证 (证明过程略)。

3.2 同时考虑有效性和个体合理性的区间值最小二乘法核仁

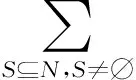
(16)

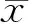
(17)

特别地，令mL=mR=0,很明显可看出，模型(8)的区间值最优解等价于模型(18)的区间值最优解，即，

(18)

模型(16)的区间值最优解等价于模型(19)的区间值最优解，即，

(19)

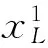
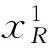
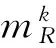
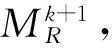
区间值最小二乘法核仁的下界和上界的算法流程分别如图1、2所示。

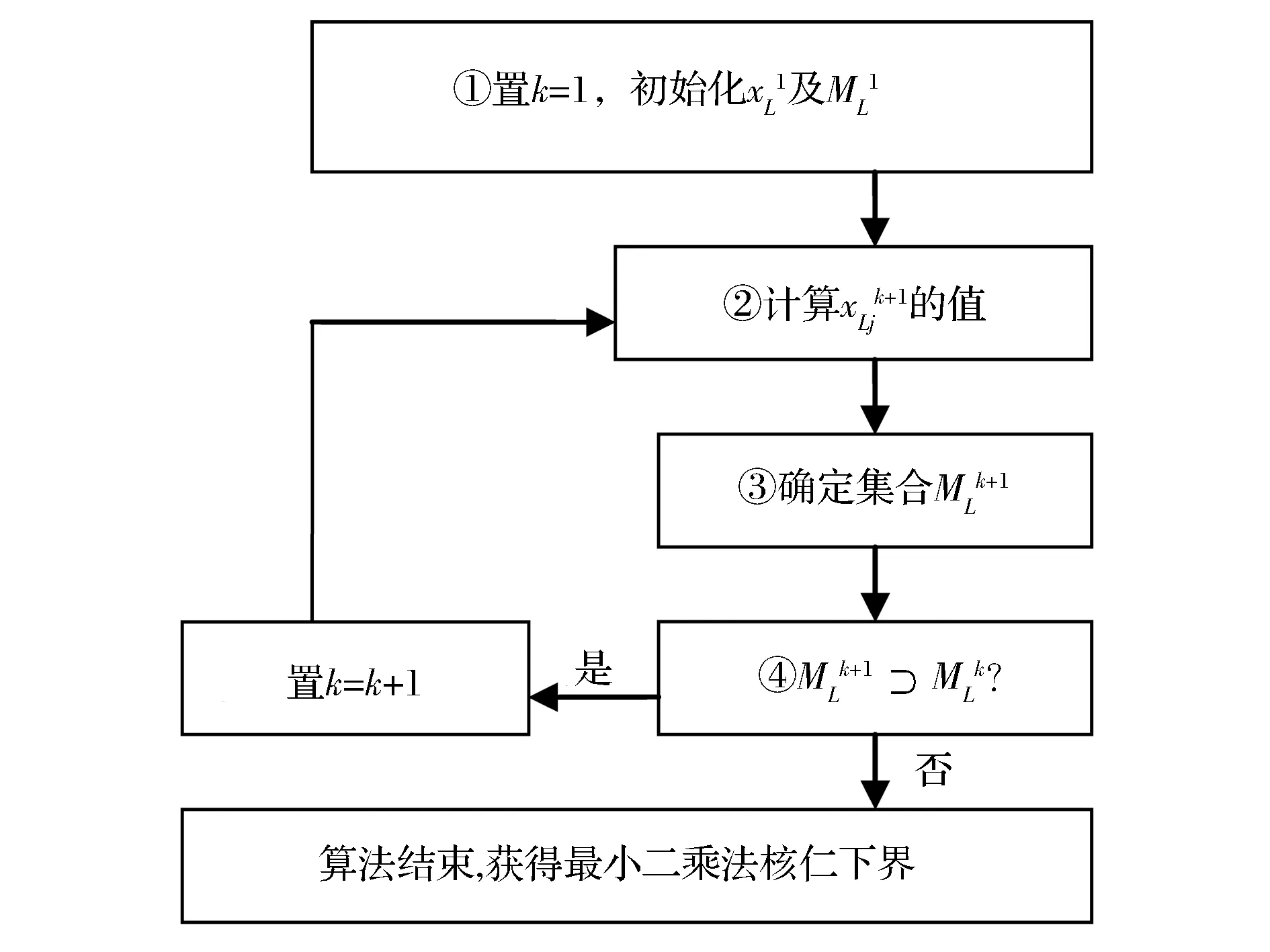
图1 区间值最小二乘法核仁下界算法流程

图2 区间值最小二乘法核仁上界算法流程

结合上面的讨论，给出求解区间值最小二乘法核仁的步骤框图，如图3所示。

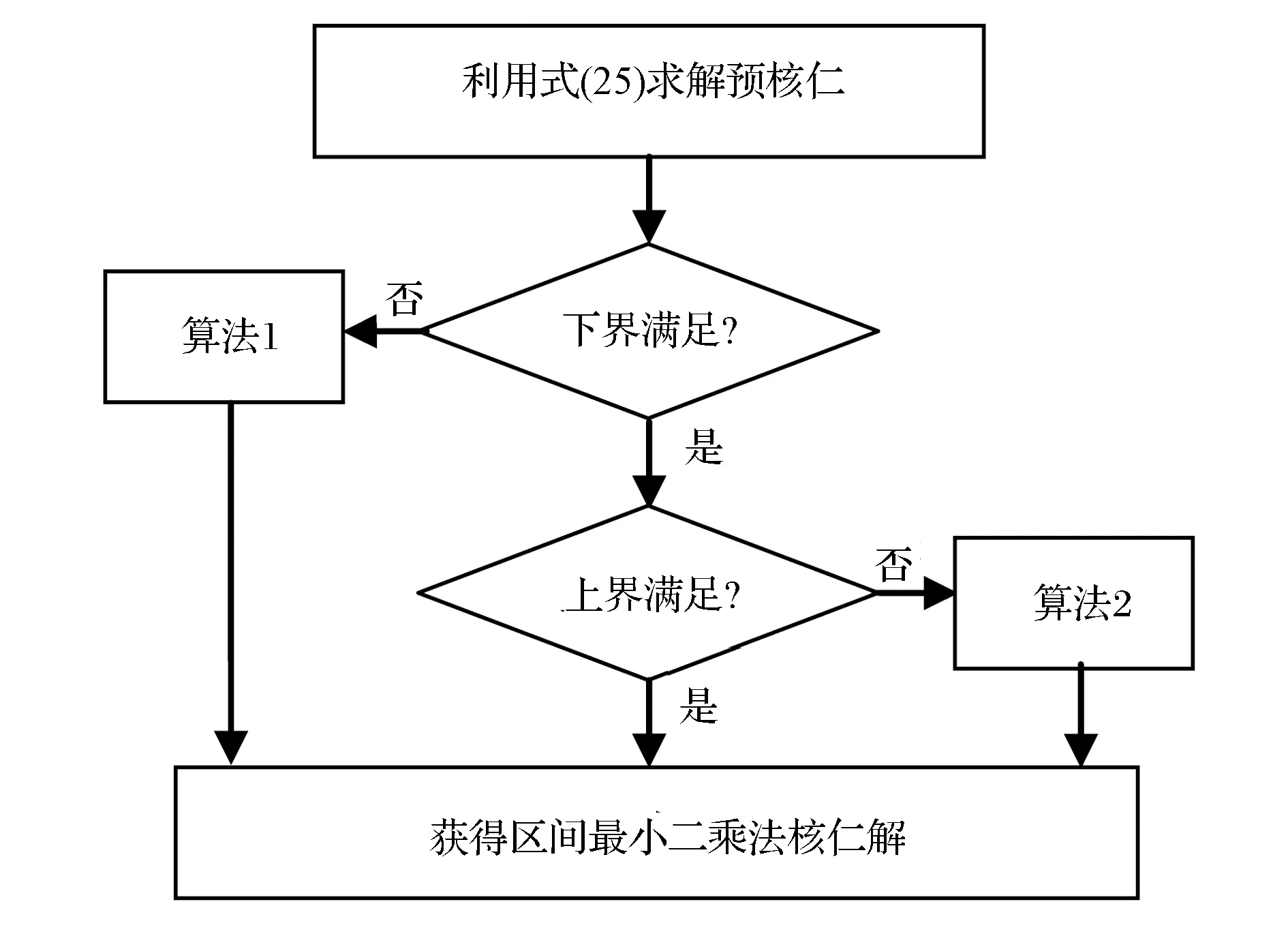
图3 区间值最小二乘法核仁的求解框图

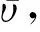
4 供应链合作创新利益分配实例应用

由于现实经济管理活动存在诸多不确定性和模糊性，区间值合作对策在经济、政治、管理、环境等多个领域均有着广泛应用。下面结合供应链合作创新中的利益分配问题，验证本文所提方法的实用性和合理性。

4.1 案例背景描述

根据式(14)，可得区间值最小二乘法预核仁的下界，即，

利用同样的方法，可计算得到，

根据算法1，有，

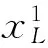
令局中人1所分配得到的收益为0，将-1.5625平均分摊给局中人2，3和4，得，

40.4167,41.6667)T

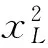
78.125)T

[37.9167,70.625],[40.4167,83.125],[41.6667,78.125])T,

即，四个节点企业的区间值收益分别为：

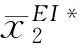
4.2 计算结果分析

在本例中，假设四个节点企业均无法单独研发新产品，即，如果供应链协同创新系统中的四个节点企业不寻求合作，他们将无法获得任何收益。然而，通过参与大联盟联合开发新产品后，四个节点企业均获得了极为可观的收入。具体如下：通过合作，原材料供应商(即局中人1)能获得最少为0、最多为18.125的收益；生产商(即局中人2)能获得最少为37.9167、最多为70.625的收益；分销商(即局中人3)能获得最少为40.4167、最多为83.125的收益；零售商(即局中人4)能获得最少为41.6667、最多为78.125的收益。根据Moore[25]的区间值运算规则，可知四个节点企业参与合作获得的区间值收益均远远大于单干时的收益，即，最终分配结果满足个体合理性。

为验证本文所提的模型和方法的合理性和有效性，用Lingo软件对上述实例进行求解。根据式(19)，在代码窗口中编写如下语句：

min=(xL1-0)2+(xR1-0)2+(xL2-0)2+(xR2-0)2+(xL3-0)2+(xR3-0)2+(xL4-0)2+(xR4-0)2+(xL1+xL2-0)2+(xR1+xR2-0)2+(xL1+xL3-0)2+(xR1+xR3-0)2+(xL1+xL4-0)2+(xR1+xR4-0)2+(xL2+xL3-80)2+(xR2+xR3-110)2+(xL2+xL4-80)2+(xR2+xR4-100)2+(xL3+xL4-80)2+(xR3+xR4-120)2+(xL1+xL2+xL3-85)2+(xR1+xR2+xR3-130)2+(xL1+xL2+xL4-90)2+(xR1+xR2+xR4-120)2+(xL1+xL3+xL4-100)2+(xR1+xR3+xR4-150)2+(xL2+xL3+xL4-100)2+(xR2+xR3+xR4-150)2+(xL1+xL2+xL3+xL4-120)2+(xR1+xR2+xR3+xR4-250)2;

xL1+xL2+xL3+xL4=120;

xR1+xR2+xR3+xR4=250;

点击Lingo软件的Solve按钮，可得到与用算法1、2求解完全一致的结果。

5 结语

本文提出的区间值最小二乘法预核仁和核仁的求解方法具有如下4个明显优点：

(1)方便、快捷、计算量小。据式(14)、(15)及算法1、2，可快速获得区间值合作对策的区间值最小二乘法预核仁和核仁。

(2)有效避免区间值减法运算。本文提出的方法未直接使用区间值减法运算，可有效避免由于区间值减法运算导致的不确定性放大等问题。

(3)分配结果合理、有效。利用部分现有区间值合作对策的求解方法，局中人分配得到的收益可能为负值，这不符合实际情况。运用本文所提方法，特别是区间值最小二乘法核仁，能确保局中人获得非负收益。

(4) 提出的解满足若干合作对策解的重要性质。本文提出的区间值最小二乘法预核仁和核仁满足诸如存在性、唯一性、有效性、可加性、对称性、匿名性等良好的性质。

本文所提方法可以很好的解决合作联盟产生的收益为区间值时的供应链合作利益分配问题，并且可以运用到经济、军事、环境、教育、科技等其他具有模糊性和不确定性的复杂合作联盟中，为其合作利益的分配提供一种新的行之有效的解决方法。尽管如此，在现实的很多经济管理问题中，有时用区间值难以贴切地表达其中的模糊性和不确定性。现实中的各种经济管理系统不仅涉及系统内部的人、物、资金、资源、信息等众多要素，而且涉及系统外的政策、环境、人文、社会习俗与行为规范等多种因素。特别地，经济管理系统不仅涉及到人，而且人是作为经济管理系统的决策主体。决策主体行为的复杂性、目标的多样性、知识经验的局限性等，进一步增加了经济管理系统的复杂不确定性。在此情境下，运用具有两标度特征的直觉模糊集能更加细腻、有效、贴切地刻画模糊性，因此，联盟值(或特征函数)表示为直觉模糊数的合作对策预核仁解和核仁解将是进一步研究的重要方向。

[1] 李登峰.模糊多目标多人决策与对策[M].北京: 国防工业出版社，2003.

[2] Branzei R, Dimitrov D, Tijs S. Models in cooperative game theory: Crisp, fuzzy and multichoice games[M]. Berlin,Heidelberg:Springer,Verlag,2005.

[3] Butnariu D. Stability and shapley value for an n-person fuzzy game[J]. Fuzzy Sets and Systems, 1980, 4(1): 63-72.

[4] Mares M. Fuzzy cooperative games: Co-operation with vague expectations[M]. Heidelberg: Physica-Verlag, 2001.

[5] Li Dengfeng. Decision and game theory in management with intuitionistic fuzzy sets[M]. Heidelberg: Springer-Verlag, 2012.

[6] 李登峰.直觉模糊集决策与对策分析方法[M].北京:国防工业出版社，2012.

[7] Aubin J P. Coeur et valeur des jeux flous à paiements latéraux[J]. C. R. Acad. Sci. Paris Sér. A, 1974, 279 (A): 891-894.

[8] Hinojosa M A, Mármol A M, Fernández F R. Set-valued cooperative games with fuzzy payoffs. The fuzzy assignment game[J]. European Journal of Operational Research, 2013, 225(1):85-90.

[9] Borkotokey S. Cooperative games with fuzzy coalitions and fuzzy characteristic functions[J]. Fuzzy Sets and Systems, 2008, 159(2): 138-151.

[10] Aubin J P. Cooperative fuzzy games[J]. Mathematics of Operations Research, 1981, 6(1): 1-13.

[11] Aubin J P. Locally lipschitz cooperative games[J]. Journal of Mathematical Economics, 1981, 8(3): 241-262.

[12] Branzei R, Dimitrov D, Tijs S. Convex fuzzy games and participation monotonic allocation schemes [J]. Fuzzy Sets and Systems, 2003, 139(2): 267-281.

[13] Branzei R, Branzei O, Alparslan Gök S Z, et al. Cooperative interval games: A survey [J]. Central European Journal of Operations Research, 2010, 18(3):397-411.

[14] Branzei R, Alparslan Gök S Z, Branzei O. Cooperative games under interval uncertainty: On the convexity of the interval undominated cores [J]. Central European Journal of Operations Research, 2011, 19(4):523-532.

[15] Alparslan Gök S Z, Branzei O, Branzei R, et al. Set-valued solution concepts using intervaltype payoffs for interval games[J]. Journal of Mathematical Economics, 2011, 47(4-5), 621-626.

[16] Alparslan Gök S Z, Branzei R, Tijs S. The interval Shapley value: An axiomatization[J]. Central European Journal of Operations Research, 2010, 18(2), 131-140.

[17] Alparslan Gök S Z, Miquel S, Tijs S. Cooperation under interval uncertainty[J]. Mathematical Methods of Operational Research, 2009, 69 (1), 99-109.

[18] Mallozzi L, Scalzo V, Tijs S. Fuzzy interval cooperative games[J]. Fuzzy sets and systems, 2011, 165(1), 98-105.

[19] Li Dengfeng. Models and methods for interval-valued cooperative games in economic management[M]. Cham, Switzerland: Springer, 2016.

[20] 于晓辉，张强.具有区间支付的合作对策的区间Shapley值[J].模糊系统与数学，2008,22(5)：151-156.

[21] 高作峰，邹正兴，马栋，等.区间合作对策在增广系统上的区间Shapley值[J].模糊系统与数学，2013,27(4)：148-156.

[22] Gillies D B. Some theorems on n-person games[M]. Princeton: Princeton University Press, 1953.

[23] Shapley L S, Shubik M. On the core of an economic system with externalities[J]. American Economic Review, 1969, 59(4): 678-684.

[24] Schmeidler D. The nucleolus of a characteristic function game[J]. SIAM Journal on Applied Mathematics, 1969, 17(6): 1163-1170.

[25] 徐伟，郑石桥，陈丹萍.闭环供应链中制造商与销售商合作创新模型研究[J].中国管理科学，2014，22(7)：116-123.

[26] 程永波，陈洪转，何利芳，等.复杂装备主制造商-供应商主从合作激励协调Stackelberg模型[J].中国管理科学，2016，24(1)：91-96.

[27] Moore R E. Methods and applications of interval analysis[M]. Philadelphia: Studies in Applied Mathematics, 1979.

[28] Ruiz L M, Valenciano F, Zarzuelo J M. The least square prenucleolus and the least square nucleolus. Two values for TU games based on the excess vector[J]. International Journal of Game Theory, 1996, 25(1):113-134.

[29] 钟昌宝，魏晓平，聂茂林，等.一种考虑风险的供应链利益两阶段分配法—正交投影熵值法[J].中国管理科学，2010，18(2)：68-74.

[30] 赵晓丽，乞建勋.供应链不同合作模式下合作利益分配机制研究—以煤电企业供应链为例[J].中国管理科学，2007，15(4)：70-76.