三峡库区卧沙溪滑坡稳定性的可靠度及敏感性分析

2018-01-24雷德鑫夏俊宝

安全与环境工程 2018年1期

雷德鑫,易武,柳青,夏俊宝

(1.三峡大学湖北省长江三峡滑坡国家野外科学观测研究站，湖北宜昌 443002;2.三峡地区地质灾害与生态环境湖北省创新协同中心，湖北宜昌 443002;3.三峡大学湖北省防灾减灾重点实验室，湖北宜昌 443002;4.兴山县国土资源局，湖北兴山 443700)

三峡工程自正常投入运营以来，水位高程在145～175 m之间周期性涨落，对库岸边坡的稳定性有着重要的影响。据统计[1]，在三峡库区内共查出崩塌、滑坡5 300余处，总体积约8.3×109m3，其中涉水崩塌滑坡1 945处，不涉水崩塌、滑坡3 411处，主要分布于长江干、支流。滑坡是三峡库区主要的地质灾害。滑坡的稳定性分析与评价一直是工程领域的核心问题，经历了由定性分析到定量分析的发展过程[2-6]。定性分析往往分析滑坡体的成因、演化，从而获得可能的失稳破坏方式与力学机理，主要包括成因历史分析法、工程地质类比法和赤平投影分析法等，由于地质条件的复杂性和人们认识事物的局限性，工程地质定性评价在斜坡稳定性评价中仍然占有很重要的地位。为了获得滑坡稳定性评价的定量指标，目前已发展了刚体极限平衡法[7]，在一定程度上满足了工程领域发展的需求，因该方法计算模型建立方便、计算过程简单，作为各行业规范的指定方法，一直被工程设计人员普遍采用。但是，传统的刚体极限平衡法只考虑了静力平衡条件和Mohr-Coulomb破坏准则，没有考虑岩土体材料的应力-应变关系和流动规则，条块划分方法及条块间相互作用力的假设比较繁琐，与实际情况存在一定的差异，且往往根据各种室内外试验确定岩土体的物理力学参数指标，对于计算参数，通过试验取得定值时得到评价滑坡体的稳定性指标也是一个确定的数值。考虑到岩土体材料的复杂性，由刚体极限平衡法计算的滑坡稳定系数仍为近似解。近年来，塑性极限分析法又称为能量法中的上下限理论为寻求滑坡稳定性计算的精确解提供了一种新的思路，能量法的基本要点是：当滑体滑动时，自重和外力所做的功率等于滑动面上阻力所消耗的功率，于是可以由滑体处于极限平衡状态时两功率相等的条件求出极限荷载、临界坡高或稳定系数[8]。但长期以来如何构造上限法的机动允许位移场和下限法的静力允许位移场一直是个难点，直到有限元单元法被引入塑性极限分析领域才成功解决这一困难，它的最大的特点是考虑了岩土体材料的应力-应变关系，物理概念清楚，计算也比较简单[9]。相较传统刚体极限平衡法，塑性极限分析法的上下限理论求解滑坡稳定性系数的分布区间，将滑坡的稳定性系数界定在一个包含精确解的小区间内，相较刚体极限平衡法计算单一的稳定系数，分布区间在一定程度上更为可信。值得注意的是，无论是刚体极限平衡法或者是塑性极限分析法，均未考虑滑坡岩土体材料的离散型，大量研究表明滑坡是既受岩土体条件控制又受各种诱因影响而发展变化的非线性动力系统[10-11]，其稳定性是内外多种因素综合作用的结果,以恒定不变的岩土体参数计算得到的确定的滑坡稳定系数往往使计算模型过于简单，得到的评价指标并不可靠，即往往计算得到安全的滑坡也存在失稳破坏的可能性。因此，基于可靠度概率分析边坡的稳定性成为一种趋势[12]。可靠度分析方法是建立在概率统计基础之上，以随机变量和随机函数为研究对象的一种非确定性分析计算方法，这种方法最本质的特点是定量地考虑工程中的不确定因素。可靠度计算考虑了岩土体物理力学属性的离散性、差异性，加之测试的各种误差，认为滑坡稳定性系数就是各种参数作用下的一个函数，从客观上来讲，稳定性系数亦为随机变量，因而采用概率分析方法来进行滑坡的稳定性评价显得更为合理。相较刚体极限平衡法和塑性极限分析法，可靠度分析既考虑了岩土体的离散型，又可分析滑坡的稳定性系数在离散岩土体参数条件下的分布区间，更符合工程实际。目前,可靠度计算方法主要有蒙特卡罗随机抽样法、点估计法、一次二阶矩法和随机有限元等[13]。

综合以上分析，本文以三峡库区卧沙溪滑坡为例，采用蒙特卡罗随机抽样法，在岩土体材料物理力学参数符合正态分布的条件下，分析了不同工况下滑坡的可靠度指标、失效概率，并分析了滑坡的稳定性系数对滑体物理力学参数的敏感性，对评价该滑坡的稳定性具有一定的指导意义，更具可靠性。

1 滑坡概况

卧沙溪滑坡位于湖北省秭归县沙镇溪镇长江支流青干河右岸(见图1)，滑坡南西高北东低，滑体后缘高程约340 m，前缘高程约140 m，滑坡左、右边界以基岩山脊与山谷交接处为界，总坡度为20°。该滑坡滑体长400 m，宽700 m，面积约为28×104m2，平均厚度约为15 m，体积约为420×104m3，主滑方向为40°，是一大型土质滑坡。

卧沙溪滑坡滑体物质主要由含碎石粉质黏土组成，其中粉质黏土呈可塑-硬塑状，土质结构稍密至松散，碎石成分以砂岩、泥岩为主，该滑体厚度自后缘至前缘一般为10～30 m，其中前缘最厚达50 m。卧沙溪滑坡的滑床为下伏基岩，即侏罗系中—下统灰绿色厚-巨厚层状长石石英砂岩、粉细砂岩夹少量紫红色粉砂质黏土岩、泥岩，岩层总体产状为100°∠25°。考虑滑坡近期变形及稳定性情况，本文选取卧沙溪滑坡1-1′典型剖面进行可靠度及敏感性分析，见图2。

图1 卧沙溪滑坡平面图Fig.1 Plannar graph of Woshaxi landslide

图2 卧沙溪滑坡1-1′剖面图Fig.2 Sectional drawing of Woshaxi landslide

2 滑坡可靠度分析的基本原理

蒙特卡罗方法又称为随机抽样技巧或统计试验方法，其基本原理如下:由概率的定义可知，某事件的概率可以用大量试验中该事件发生的频率来估算，当样本容量足够大时，该事件发生的频率即为概率。因此，对影响滑坡可靠度的随机变量进行大量抽样，并代入功能函数式，即可建立滑坡稳定性状态函数：

Fj=g(x1,x2,…,xm)

(1)

其中，x1,x2,…,xm为控制滑坡稳定性的随机变量。

可由公式(1)得到滑坡的稳定性系数Fj，如此重复N次，便可得到N个相对独立的滑坡稳定性系数样本值F1,F2,…,FN，若定义{Fj<1}为滑坡失效事件，且在N次抽样中出现M次，则滑坡失效概率Pf为

Pf=P(Fj<1)=MN

(2)

公式(2)即为用蒙特卡罗随机抽样法计算出的滑坡失效概率，其均值μF和标准偏差σF为

μF=1N∑Nj=1Fj

(3)

σF=(1N-1∑Nj=1(Fj-μF)2)12

(4)

β=μF-σF

(5)

岩土工程中假定当稳定性系数Fs=1时，边坡处于临界状态，则相对于Fs=1时的可靠度指标称为绝对可靠度指标β，其可表示为

β=μF-1σF

(6)

则滑坡失效概率为

Pf=1-φ(β)

(7)

3 滑坡计算模型建立与滑坡体物理力学参数确定

3. 1 滑坡计算模型的建立

本文综合运用Geo-Studio中Seep-w和Slope-w两个模块，对卧沙溪滑坡的渗流场和稳定性进行模拟。其中，Slope-w模块中采用Morgenstern-Price算法，建立的滑坡计算模型见图3，其中该计算模共划分为1 354个单元、1 416个节点。

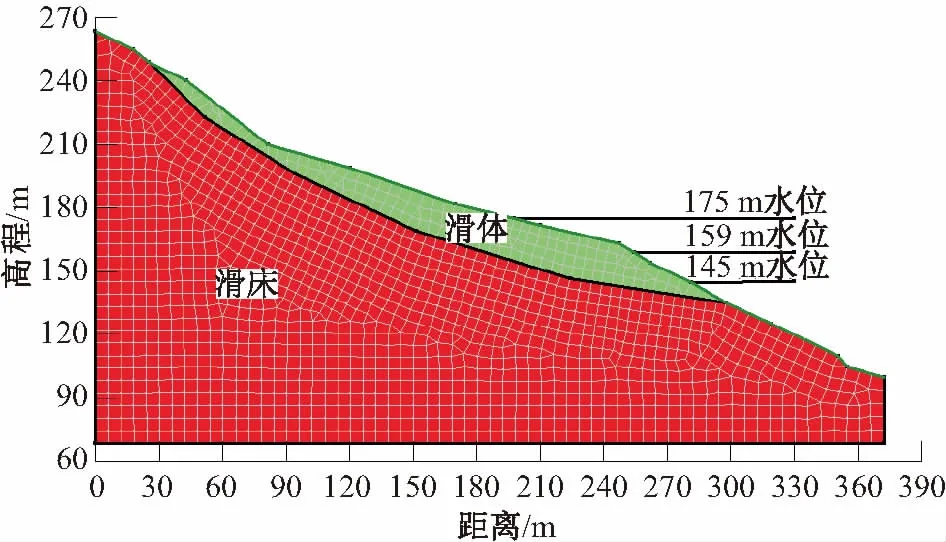
图3 卧沙溪滑坡计算模型Fig.3 Calculation model of Woshaxi landslide

3. 2 滑坡体物理力学参数的确定

大部分土工材料的参数分布都符合正态概率密度函数，本文结合相关勘察资料，通过室内直剪试验、三轴压缩试验等确定卧沙溪滑坡体的物理力学参数(黏聚力c、内摩擦角φ、重度γ)，并建立了滑坡体物理力学参数的正态分布函数，详见表1。

表1 卧沙溪滑坡的物理力学参数

4 滑坡的可靠度及敏感性分析

4. 1 滑坡计算工况设计

库水位的周期性抬升和下降导致滑坡体内部渗流场的改变，尤其是库水位快速下降时地下水渗流所引起的动水压力，是滑坡失稳变形的主要原因。因此，为了研究在不同库水位下降速度与降雨的综合作用下卧沙溪滑坡的可靠度及失效概率，本文考虑了最不利工况组合，主要设计了2种工况组合，详见表2。其中，最大库水位降速为1.3 m/d，最低库水位降速为0.6 m/d；降雨强度按照暴雨强度重现期为50年一遇标准考虑，根据秭归县2002—2010年9年降雨量统计和降雨强度重现期分析，4～6月份期间，连续3天50年一遇降雨强度值一般在176 mm左右，按照3天平均分配，每天降雨强度值为55.33 mm，为降雨入渗计算提供初始条件。工况1-2条件下，降雨添加时间为库水位变动159～157.2 m区间内，工况2-2条件下降雨添加时间为库水位变动159～156 m区间内。

表2 卧沙溪滑坡计算工况

4. 2 滑坡可靠度及失效概率分析

在岩土体参数符合正态分布的情况下，本研究进行2 000次蒙特卡洛随机抽样模拟，计算卧沙溪滑坡在各种工况条件下的可靠度指标、失效概率，并分析滑坡稳定性系数对滑体物理力学参数c、φ、γ的敏感性。不同工况条件下的卧沙溪滑坡稳定性系数的分布区间，见图4和图5。

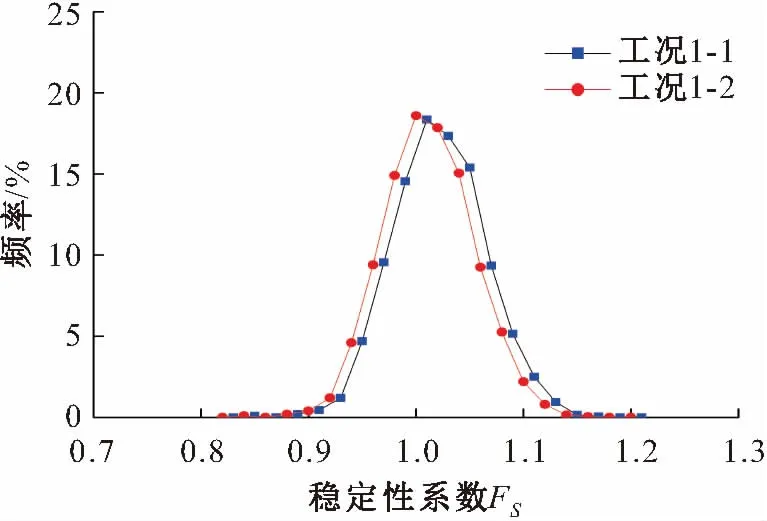
图4 工况1条件下卧沙溪滑坡稳定性系数的分布区间Fig.4 Distribution interval of landslide safety factors under the working condition 1

由图4可见，工况1-1条件下，滑坡平均稳定性系数Fs为1.032，标准偏差σF为0.042，可靠度指标β为0.757；工况1-2条件下，卧沙溪滑坡平均稳定性系数Fs为1.022，标准偏差σF为0.042，可靠度指标β为0.516。

图5 工况2条件下卧沙溪滑坡稳定性系数的分布区间Fig.5 Distribution interval of landslide safety factorsunder the working condition 2

由图5可见，工况2-1条件下，卧沙溪滑坡平均稳定系数Fs为1.022，标准偏差σF为0.042，可靠度指标β为0.534；工况2-2条件下，卧沙溪滑坡平均稳定系数Fs=1.010，标准偏差σF=0.041，可靠度指标β为0.235。

通过计算不同时刻下卧沙溪滑坡的失效概率Pf，可得到不同工况条件下卧沙溪滑坡失效概率随库水位高程变化的关系曲线，见图6。

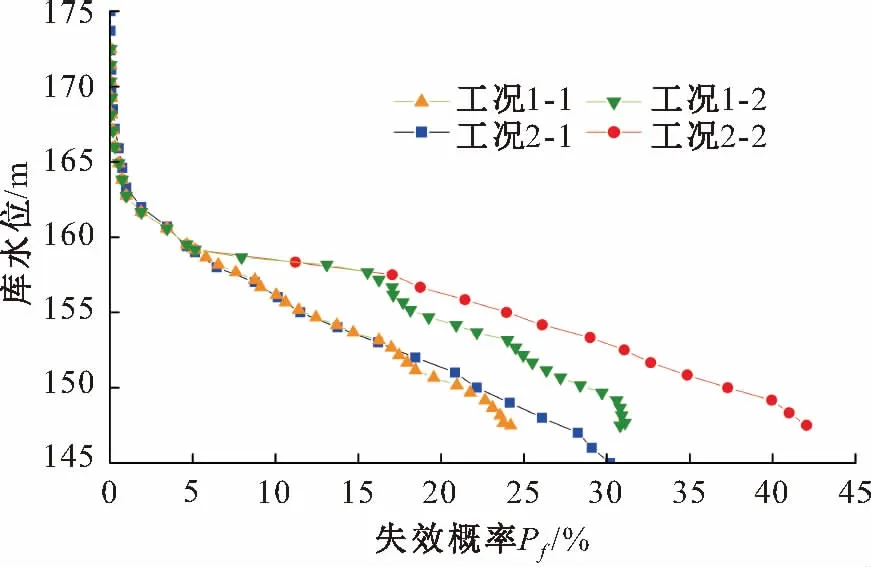
图6 不同工况条件下卧沙溪滑坡失效概率与库水位的关系曲线Fig.6 Relationship between failure probability and reservoir water level under different working conditions

由图6可见，库水位下降初始阶段，各种工况条件下滑坡失效概率随库水位均变化较小，但随着时间的增加，库水位持续下降，各种工况条件下该滑坡失效概率均较初始阶段明显增大，且库水位下降速率越大，滑坡失效概率越大，且当叠加了暴雨工况后，滑坡失效概率呈跳跃式增大，相较天然库水位下降工况下均大大增加，其中以工况2-2条件下卧沙溪滑坡的失效概率最大，其值可达42.05%。

综合以上分析，卧沙溪滑坡具有动水压力型滑坡[14-15]的特征，滑坡滑体物质为含碎石粉质黏土，渗透性较差，当库水位下降时，由于滑坡体内地下水下降滞后于库水位下降，形成了指向滑坡体外部的动水头压力，因此在库水位下降初始阶段，动水头压力较小，低于库水位反向作用于滑坡体上的压力，滑坡破坏概率较小；但随着时间的增加，动水头压力显著增大，库水位反向作用于滑坡体上的压力持续减小，滑坡可靠度降低，破坏概率明显增大，且库水位下降速率越大，动水头压力越大，滑坡失效概率越大；当在叠加了暴雨工况后，滑坡失效概率相对于天然状态下明显增大，可见降雨对滑坡失稳破坏具有明显的促进作用，尤其在库水位快速下降时遭遇暴雨条件，对滑坡的稳定性更为不利。

4. 3 滑坡敏感性分析

大量研究表明，滑坡稳定性系数与滑体重度γ、黏聚力c、内摩擦角φ关系密切，本文着重分析了不同库水位波动速率条件下滑坡的稳定性系数对滑体的物理力学参数c、φ、γ的敏感性，其分析结果见图7和图8。

图7 卧沙溪滑坡在工况1-1条件下的敏感性分析Fig.7 Sensitivity analysis under working condition 1-1

由图7可见，在工况1-1条件下，卧沙溪滑坡的稳定性系数与滑体c、φ的敏感性关系曲线斜率均大于0，且φ的敏感性关系曲线斜率大于c的，说明该滑坡的稳定性系数与滑体c、φ呈正相关关系，且滑坡稳定性系数对φ更为敏感；而卧沙溪滑坡稳定性系数与滑体γ的敏感性关系曲线斜率接近或稍大于0，说明工况1-1条件下，该滑坡性稳定系数对滑体γ不敏感。

图8 卧沙溪滑坡在工况2-1条件下的敏感性分析Fig.8 Sensitivity analysis under working condition 2-1

由图8可见，在工况2-1条件下，卧沙溪滑坡的稳定性系数对c、φ的敏感性与工况1的情况大致类似，但相对工况1-1，滑体γ敏感性关系曲线斜率小于0，其斜率绝对值较工况1-1明显增大，说明工况2-1条件下使滑坡稳定性系数对滑体γ的敏感性得到一定的增强。综合以上分析，卧沙溪滑坡的稳定性系数与滑体φ、c呈正相关关系，且对φ更敏感；而对不同库水位下降速率条件下滑体γ的敏感性分析可知，库水位下降速率越大，滑坡稳定性系数与滑体γ的负相关性越强，滑坡越不稳定，分析认为库水位下降速率越大，滑坡体内地下水不能及时排出，形成高水头差，滑坡体γ越大，由渗流力引起的下滑力也就越大，越不利于滑坡的稳定，也说明了卧沙溪滑坡具有典型的动水压力型滑坡的特征。