基于化学反应优化算法的导弹鲁棒PID控制器设计

马珍珍 陈欣 张民

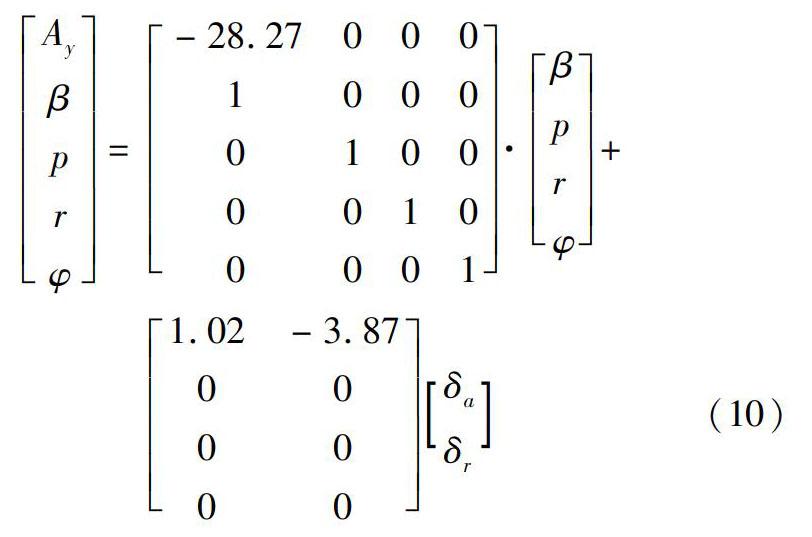
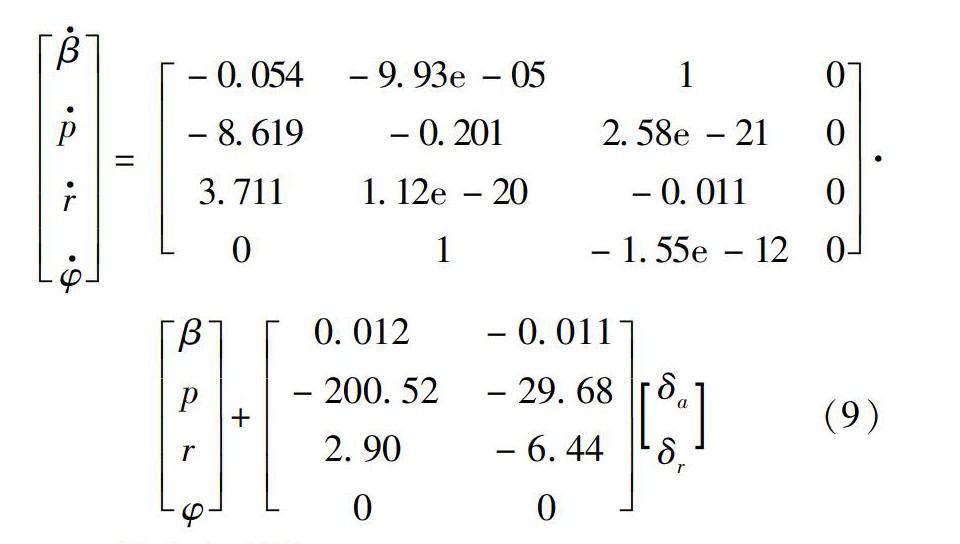
摘 要：由于现代空空导弹的非线性、 强耦合气动特性， 传统基于SISO模型的PID控制器整定方法难以满足当前很高的控制性能要求， 为了满足导弹某些极限状态的控制需求， 对控制系统的鲁棒性提出了更高的要求。 为此本文研究了一种基于化学反应优化算法的H∞-PID鲁棒控制器设计方法， 并将其应用于样例空空导弹横侧向通道控制。 仿真结果表明了本文提出的控制器设计方法的优越性。

关键词： 导弹; 鲁棒控制; PID控制; 混合灵敏度H∞控制; 化学反应优化

中图分类号： TJ765; TP273 文献标识码：A 文章编号： 1673-5048（2018）05-0036-05[SQ0]

0 引言

作为一种鲁棒控制方法， H∞控制理论已广泛应用于控制器设计中[1]， 但在导弹控制的实际工程应用中， H∞控制理论设计出的控制器往往阶数过高以致于难以工程化实现， 对控制器进行降阶又可能带来不可预测的性能退化问题， 因此， 研究一种鲁棒PID控制器十分必要。 随着智能优化算法的发展， 利用这些算法可以快速、 方便、 智能地解决此类问题[2]。 本文研究了一种基于化学反应优化算法的H∞-PID控制器优化整定方法， 通过对动态性能指标和H∞鲁棒性指标的极小值寻优， 使设计的控制器既具有PID控制器简单实用、 易于实现的特点， 又具有H∞控制器的鲁棒性能， 并将其应用于样例空空导弹驾驶仪横侧向通道的设计中。

1 化學反应优化算法

化学反应优化（Chemical Reaction Optimization， CRO）算法是以自然界中化学反应为灵感来源的一种新兴的智能优化算法， 是Albert Y.S.Lam等人[3]于2010年首次提出， 并成功应用于二次分配问题和资源受限项目调度问题。 CRO算法基于化学反应过程中有着向能量较低方向进行的趋势以及热力学两大定律， 即能量守恒定律和熵增原理， 将问题的解看作化学反应中分子的结构， 每个分子分别赋予各自的属性， 通过模拟化学反应的过程， 寻求分子属性中关于势能这一项的最优值来得到最佳的解。 从2010年至今， 此优化算法已经有效地解决了许多应用领域的问题， 如网格计算中的任务调度问题[4]、 异构计算系统的任务调度问题[5]、 旅行商问题[6]、 经济调度问题[7]等。 CRO算法具有以下四个特点：

（1） 算法的框架中具有不同的算子， 适用于不同的问题;

（2） 算法的优越性依赖于不同形式下的能量守恒与能量转换;

（3） 分子的结构中可以引入其他的属性特质， 这使得CRO算法更加的灵活;

（4） CRO算法具有收敛速度快、 鲁棒性强的特点， 并且可以避免陷入局部最优。

CRO算法包括三个基本步骤：

（1） 初始化

CRO算法的初始化包括分子属性的分子结构（ω）、 种群大小（PopSize）、 初始动能（InutialKE）、 碰撞次数（NumHit）、 最小碰撞次数（MinHit）等参数的初始化以及用于判断条件的系统参数的初始化， 如用于判断选择一个分子还是两个分子反应而产生的参数（MoleColl）、 用于判断是否发生分解反应的参数（α）和用于判断是否发生化合反应的参数（β）。

（2） 迭代

在迭代的过程中， 就是化学反应发生的过程， 每一次迭代代表着发生了一次化学反应， 利用单分子无效碰撞反应（OnwallIneffColl）、 分子间无效碰撞反应（IntermoleIneffColl）、 分解反应（Decompositin）和化合反应（Synthesis）这四种反应算子将问题收敛到最优解。 初始能量由初始种群大小、 分子初始动能和中间缓冲能量决定， 即

式中： PEωi（t）， KEωi（t）， buffer（t）， PopSize（t）分别为t时刻第i个分子的势能、 动能、 中间缓冲能量和分子种群大小; C是不变的。

首先通过一个随机参数z∈[0，1]来判断是单分子碰撞反应还是分子间碰撞反应， 如果z>MoleColl， 则发生单分子碰撞， 反之则发生分子间碰撞。 对于单分子碰撞反应， 检查是否满足分解反应标准， 即MinHit-NumHit≥α， 如果满足此条件， 则发生分解反应， 反之则发生单分子无效碰撞; 对于分子间碰撞反应， 检查是否满足化合反应标准， 即KE≤β。 由于分子间碰撞至少有两个分子参与， 因此每一个反应分子须满足此条件， 才能发生化合反应， 否则， 发生分子间无效碰撞。 每一次反应之后得到的最小解存放在最小分子结构（MinStruct）和最小势能（MinPE）中。 四种反应的能量守恒条件也是用来判断反应成功与否的条件， 如下：

式中： PE， KE为分子的势能和动能; ω， ω′为反应前后的分子; δ1， δ2为[0，1]之间的随机数。

（3） 算法终止判断

判断算法是否找到最优解或者达到算法最大迭代次数， 如果是则终止迭代， 输出最优解; 否则返回步骤（2）继续迭代。

2 基于CRO算法的混合灵敏度H∞-PID控制器设计

控制系统的鲁棒性是指控制系统在一定的参数摄动下能够保持稳定并满足控制性能要求。 混合灵敏度法是H∞控制理论中广泛应用的一种方法。 令G为控制对象， K为控制器， 那么开环传递函数L=GK; 灵敏度函数S=（1-L）-1， S反映系统输出对干扰的抑制能力; 补灵敏度函数T=L/（1-L）-1， 与系统的稳定鲁棒性有关[8]。

标准H∞控制问题的混合灵敏度设计问题方框图如图1所示， 其中： W1（s）为性能权函数， 是对系统性能要求的约束， 通过调整可以有效地抑制干扰; W2（s）反映了对控制信号幅值的约束， 一般W2（s）为0， 以保证闭环控制系统鲁棒稳定性的要求; W3（s）为模型不确定性界函数， 反映了对乘性不确定性的限制和鲁棒稳定性要求[9];y1为系统的评价信号;y2为测量信号;u1为外部输入信号;u2为H∞控制器输出信号;e为跟踪误差;u为控制信号; y为输出信号; K（s）为H∞控制器; G为被控对象。

混合灵敏度问题实际就是通过合理地选择权函数[10]， 找到一控制器K（s）， 使得闭环控制系统稳定， 且满足P∞<1， 即

根据一般的权函数选择规则， W1在低频段的幅值应尽量大， 而W2的幅值在高频段应尽量大[11]， 由此鲁棒PID控制器设计就转化成了找到一个PID控制器替代K（s）并满足原控制系统的各项性能指标。

本文选用经典Raytheon驾驶仪控制结构为导弹PID控制器， 其横侧向控制结构如图2所示。

图中φ， φg分别为滚转角反馈信号和外部给定滚转角信号; Ay， Ayg分别为侧向加速度反馈信号和外部侧向加速度信号，  p， ψ， r分别为滚转角速率、 偏航角和偏航角速率。 δa和δr分别为副翼舵偏角和方向舵偏角。 图2中的控制律如下式所示：

样例导弹横侧向通道需满足表1所示的时域性能指标。

上升时间超调量稳态误差

性能指标≤0.3 s≤20%≤2%

为了优化导弹控制的动态特性并满足鲁棒性， 应用CRO算法对控制器的各项性能指标寻优， 需要考虑以下三个性能指标：

（1） 时间乘绝对误差积分准则（ITAE）： 通常智能优化算法会采用IAE， ISE， ITAE等误差积分准则作为衡量指标[11]， 将ITAE作为控制器的动态性能指标， 能使得控制系统瞬态响应的振荡性小、 调节时间短， 能较好地抑制長时间存在的误差。

（2） 超调量（Os）： 一般情况下， 提高控制系统的快速性必然会带来一定超调量， 将超调量指标考虑在寻优的过程中， 能对其进行有效抑制[12]。

（3） 闭环控制系统的H∞值：这个指标表征系统的鲁棒性能， H∞值越小， 系统的鲁棒性越强。

因此， 基于CRO算法的混合灵敏度H∞-PID控制器方法的目标函数如下式所示：

式中： w1， w2， w3为权重因子， 可以根据被控对象的特性以及系统不同的性能来取值。 利用CRO算法优化目标函数J的极小值， 从而找到满足各项性能指标的PID控制器参数。

3 仿真验证

本文中的控制律设计以MIMO线性化模型为设计对象， 以样例空空导弹在20 000 m高度、 2.0马赫、 30°攻角下的特征工作点横侧向通道状态空间模型为例， 其状态方程为

1.02-3.87000000δaδr（10）

式中： β， p， r， φ分别为侧滑角、 滚转角速率、 偏航角速率和滚转角; Ay为侧向加速度; δa和δr分别为等效副翼舵偏角和方向舵偏角。

本文基于H∞混合灵敏度法的权函数如下所示：

由于控制参数均为正值， 为了缩小搜索空间的范围， 将待寻优的控制参数转换为

x=（x1， x2， x3， x4， x5， x6， x7）T=（log10ka1， log10ka2， log10kr1， log10kr2， log10kr3，

log10kr4， log10kr5）T（12）

此时， 待寻优参数的范围可以设置为

为了验证、 对比算法的性能， 分别采用差分进化算法（DE）[13]， 模拟退火法（SA）[14]和本文的CRO算法对导弹控制器的参数进行寻优。 DE和SA算法采用与文献中的相同参数进行优化， CRO算法的初始参数取为： 种群大小为10， 反应步长为0.001， 初始动能为1 000， buffer初始值为0， MoleColl为0.2， α为1 000， β为10， 迭代次数为1 000， 终止条件是达到最大代数。

表2为分别采用上述三种算法得到的寻优结果， 是由每一种算法运行20次后的平均值得到的， 式（8）中的参数w1， w2， w3分别为0.01， 1， 1。 表3为三种算法运行20次、 每次迭代的平均计算时间。 三种算法得到的控制器在侧向过载和滚转角的阶跃响应下的输出曲线如图3～4所示。 采用DE算法得到的PID控制在侧向过载响应上具有较大的超调， 而SA算法得到的控制结果在滚转角响应有较大的超调， 而且在侧向过载响应中的调节时间较长。 CRO算法得到的控制结果能同时满

足这两个指令的阶跃响应， 具有较快的调节时间。

混合灵敏度函数和补混合灵敏度函数波特图如图5～6所示， 可以看出， 灵敏度函数S（s;x）

和补灵敏度函数T（s; x）的曲线始终分别处于W-11（s）（即inv

（W1））和W-13（s）（即inv（W3））函数曲线的下方， 满足H∞ 控制要求， 表明了控制系统的高鲁棒性能。

4 结 束 语

本文采用H∞混合灵敏度控制理论， 结合CRO优化算法对导弹横侧向通道进行了鲁棒PID控制器的设计。 仿真实验表明， 所提出的基于CRO的鲁棒PID控制器优化设计方法能直接对导弹MIMO系统模型展开设计， 自动得到PID控制参数， 并能有效提高闭环系统的时域响应特性和鲁棒性。

参考文献：

[1] 郑建华， 杨涤. 鲁棒控制理论在倾斜转弯导弹中的应用[M]. 北京： 国防工业出版社， 2001.

Zheng Jianhua， Yang Di. The Application of Robust Control Theory to Bank to Turn Missile[M]. Beijing： National Defense Industry Press， 2001. （in Chinese）

[2] Hooshmand R A， Amooshahi H， Parastegari M. A Hybrid Intelligent Algorithm Based Short Term Load Forecasting Approach[J]. International Journal of Electrical Power & Energy Systems， 2013， 45（1）： 313-324.

[3] Lam A Y S， Li V O K. Chemical Reaction Optimization： A Tutorial[J]. Memetic Computing， 2012， 4（1）： 3-17.

[4] Xu J， Lam A Y S， Li V O K. Chemical Reaction Optimization for Task Scheduling in Grid Computing[J]. IEEE Transactions on Parallel and Distributed Systems， 2011， 22（10）： 1624-1631.

[5] Xu Yuming， Li Kenli， He Ligang， et al. A DAG Scheduling Scheme on Heterogeneous Computing Systems Using Double Molecular Structure Based Chemical Reaction Optimization[J]. Journal of Parallel and Distributed Computing， 2013， 73（9）： 1306-1322.

[6] Bouzoubia S， Layeb A， Chikhi S. Enhanced Chemical Reaction Optimization for Multi Objective Traveling Salesman Problem[C]∥

Proceedings of the 4th International Symposium， Modelling and Implementation of Complex Systems， Constantine， Algeria， 2016.

[7] Roy P K， Hazra S. Economic Emission Dispatch for Wind Fossil Fuel Based Power System Using Chemical Reaction Optimisation[J]. International Transactions on Electrical Energy Systems， 2014， 25（12）： 3248-3274.

[8] Doyle J C， Glover K， Khargonekar P P， et al. State Space Solutions to Standard H/Sub 2/ and H/Sub Infinity / Control Problems[J]. IEEE Transactions on Automatic Control， 1989， 34（8）： 831-847.

[9] 張金鹏， 罗德林， 曹有亮. BTT导弹鲁棒飞行控制系统设计[J]. 航空兵器， 2017（5）： 11-17.

Zhang Jinpeng， Luo Delin， Cao Youliang.Robust Flight Control System Design for BTT Missile[J].Aero Weaponry， 2017（5）： 11-17.（in Chinese）.

[10]

王杰， 王栓， 朱晓东， 等. 基于约束多目标免疫算法的H∞混合灵敏度加权阵选择[J]. 电力自动化设备， 2009， 29（1）： 37-40.

Wang Jie， Wang Shuan， Zhu Xiaodong， et al. Weighting Function Matrix Selection for Mixed Sensitivity in H∞ Robust Control Based on CMO Immune Algorithm[J]. Electric Power Automation Equipment， 2009， 29（1）： 37-40.（in Chinese）

[11] Chen Zhihuan， Yuan Xiaohui， Ji Bin， et al. Design of a Fractional Order PID Controller for Hydraulic Turbine Regulating System Using Chaotic Non Dominated Sorting Genetic Algorithm II[J]. Energy Conversion and Management， 2014， 84： 390-404.

[12] Shabani H， Vahidi B， Ebrahimpour M. A Robust PID Controller Based on Imperialist Competitive Algorithm for Load Frequency Control of Power Systems[J]. ISA Transactions， 2013， 52（1）： 88-95.

[13] Qin A K， Huang V L， Suganthan P N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization[J]. IEEE Transactions on Evolutionary Computation， 2009， 13（2）： 398-417.

[14] Bertsimas D， Tsitsiklis J. Simulated Annealing[J]. Statistical Science， 1993， 8（1）： 10-15.

Missile Robust PID Controller Design Based on

Chemical Reaction Optimization Algorithm

Ma Zhenzhen， Chen Xin， Zhang Min

（College of Automation Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China）

Abstract：In view of the strong coupling and non linearity of the air to airmissile system， the traditional PID controller tuning method cannot meet the required control performance. In order to meet some limit control requirements of the missile，higher requirements for the robustness of the control system areput forward. For this reason， a kind of optimal design method of robust H∞ PID controller based on chemical reaction optimization algorithm is proposed， and it is applied to air to airmissile lateral channel control.The results show that the proposed controller design method is effective and superior.

Key words：missile; robust control; PID control; mixed sensitivity H∞ control; chemical reaction optimization