励磁线圈磁场约束金属射流变形的作用机理研究

孟学平， 雷 彬， 向红军， 吕庆敖， 黄 旭

(军械工程学院 弹药工程系，石家庄 050003)

破甲弹作为陆基作战平台发射弹药的一种，其对坦克装甲具有很大的杀伤作用，在现代和未来地面战争中发挥着重要作用，其利用聚能装药爆炸压垮金属药型罩，产生细长的、具有很强穿透能力的高速金属射流(尾部速度为2 km/s，头部速度可达10 km/s)对目标进行有效毁伤[1]。2001年，Karlsson[2]利用欧拉网格法对金属射流的产生、拉伸及失稳过程进行了数值模拟，分析了金属射流对目标靶板的侵彻机制。2007年，Horsfall等[3]分析了间隔复合装甲对金属射流作用效果的影响，研究表明，间隔复合装甲可有效减弱金属射流的毁伤效果，且复合装甲间隔变化对金属射流毁伤效果影响较大。在面对新型军事目标时，现有破甲弹威力增强方法已经遇到瓶颈，需寻求新原理新方法，来增强破甲弹对目标的毁伤效果。

外部施加磁场对金属射流变形及形成过程具有较强的驱动作用，欧美等发达国家科研人员对此进行了具体研究。Shvetsov等[4-6]针对被动电磁装甲对金属射流的作用效果进行了相关研究，建立了被动电磁装甲作用下金属射流对目标靶板侵彻穿深的物理模型，运用数值模拟和实验验证相结合的方法，得出被动电磁装甲可对金属射流施加箍缩电磁力作用，加速金属射流劲缩部位断裂过程，进而减弱金属射流对目标靶板的侵彻穿深能力。2007年，Fedorov等[7]研究了金属射流形成初期施加外部磁场对其作用效果的影响，外部磁场覆盖整个金属药型罩，结果表明，外部施加磁场作用下金属射流对目标靶板的侵彻穿深能力大大降低。2010年，Fedorov等[8]基于建立的外部磁场作用下金属射流拉伸物理模型，对处于拉伸状态金属射流的磁流体不稳定性进行了相关研究，预测了金属射流在外部施加磁场作用下的拉伸延长，最后对金属射流不同部位在外部施加磁场作用下有效长度的增量进行了探讨。2013年，Fedorov等[9]建立了被动电磁装甲模型，分析了被动电磁装甲对金属射流的约束作用，结果表明，金属射流颈缩部位在被动电磁装甲箍缩电磁力作用下会加速断裂，破甲弹对目标的毁伤效果减弱。2014年，Grace等[10]通过在金属药型罩中馈入脉冲电流的方法，对电磁力驱动金属药型罩产生金属射流的可行性进行了分析，结果表明，当馈入金属药型罩内的脉冲电流峰值达到兆安级时，在电磁力驱动和欧姆热引起的金属材料软化作用下产生的金属射流类似于聚能装药爆炸产生的金属射流。

根据相关研究现状分析可得，目前外部施加磁场对金属射流作用的相关研究重点是被动电磁装甲对金属射流的作用效果的影响和利用电磁能驱动产生金属射流，只有俄罗斯科研人员研究了外部施加磁场对金属射流毁伤效果的增强作用，重点分析了外部施加磁场作用下金属射流磁场的变化规律，并未针对金属射流在外部施加磁场作用下的变形机理进行深入分析。本文提出一种有效控制金属射流变形过程的方法，该方法利用螺线管线圈产生脉冲电磁场，进而形成强大电磁力作用，驱动金属射流发生有效变形。基于外部施加磁场对金属射流作用的基本原理，采用理论分析、数值计算与试验验证相结合的方法，分析励磁线圈磁场作用下金属射流电磁场、温度场及结构场的变化规律，掌握励磁线圈磁场约束金属射流变形的作用机理。

1 理论分析

1.1 电磁场模型

图1为励磁线圈磁场对金属射流的施加作用的原理图。当雷管被点燃后，聚能装药随之被引燃，金属药型罩在强烈的爆轰波作用下被迅速压垮，产生高速金属射流，金属射流是处于固态和液态之间的塑性体状态，其在毁伤目标前会产生颈缩，颈缩过程发展会导致金属射流发生断裂，其有效长度达到缩短，进而使得破甲弹对目标的毁伤效果明显减弱。在金属射流发生颈缩但并未断裂为各个单元的过程中，如果在金属射流外部施加磁场，可使得金属射流颈缩部位受到较大电磁力作用，由于金属射流颈缩部位直径不同，故其所受电磁力大小不同，凸起部分所受径向电磁力大于凹陷部分对应值，进而形成电磁力差，当电磁力差大于金属射流材料的等效流动极限时，金属射流随即发生轴向流动，凸起部分材料质点流向凹陷部分，金属射流颈缩部位直径差因此减小，有效长度延长，其颈缩断裂过程被延缓，最终使得金属射流对目标的毁伤效果增强。

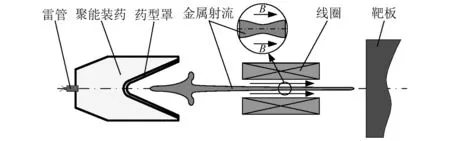
图1 励磁线圈磁场对破甲弹金属射流的作用原理Fig.1 Action principle of magnetic field of coil on shaped charge jet (SCJ)

金属射流二维模型如图2所示。

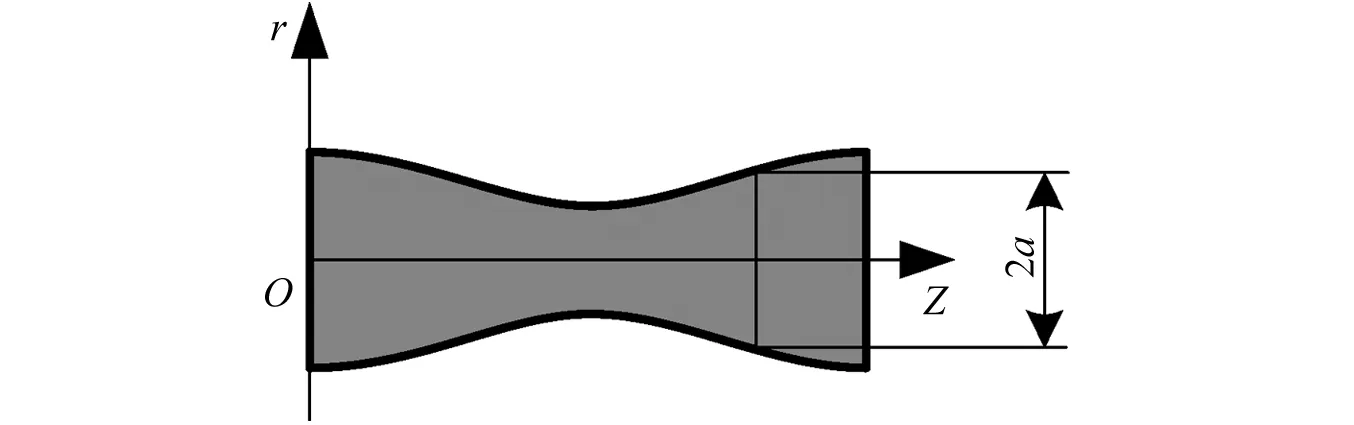
图2 金属射流二维模型Fig.2 The 2D model of SCJ

假定金属射流轴向位置为z处横截面直径为2a(a=bcosω0z+c，其中b，ω0和c为常量)，金属射流外部励磁线圈脉冲电流频率为f(角频率为ω=2πf)，H0r和H0z分别为金属射流周围的励磁线圈磁场强度，与金属射流感应磁场密切相关。模型假定励磁线圈长度大于金属射流微元长度，以便消除励磁线圈磁场边缘效应的影响。

由电动力学知识可得，金属射流磁场强度只存在轴向和径向分量，周向分量为零，即

H(r,z,ω,t)=H(r)eiωtez+H(z)eiωter

(1)

磁场强度可用贝塞尔方程来表示，结合麦克斯韦方程组[11-12]、贝塞尔函数，利用金属射流与周围介质的边值关系，可得到金属射流磁感应强度及感应电流密度分布理论模型为

(2)

式中：μ、σ、ω分别为相对磁导率、电导率及脉冲电流频率；J0和J1分别为零阶和一阶第一类贝塞尔函数。

励磁线圈对金属射流施加的作用力为安培力，单位安培力可表示为

dF=j×BdV

(3)

随着励磁线圈中脉冲电流频率变化，金属射流中感应电流密度、磁感应强度及电磁力等均会呈现不同程度的趋肤效应，趋肤深度可表示为

(4)

式(2)和式(3)即为金属射流在励磁线圈磁场作用下的电磁场分布理论模型。由式(2)分析可知，在线圈加载电流频率一定的情况下，金属射流中电磁场分布与其半径、轴向位置及励磁线圈脉冲电流频率等有关；当脉冲电流由多个频率成分组成时，磁场和感应电流的变化规律还与脉冲电流频率组成成分相关，励磁线圈脉冲电流频率直接决定金属射流中电磁场的扩散程度；由式(3)得出，金属射流所受电磁力由感应电流密度和金属射流磁感应强度决定，励磁线圈脉冲电流对金属射流电磁场分布有着很大影响。

1.2 温度场及结构场模型

由于金属射流可以看作塑性体，而作为材料的本构模型，Johnson-Cook模型[13-14]故能够很好地描述大多数金属的动力塑性行为，其表达式为

(5)

以上即为材料的本构模型，对某种特定材料，式中：A，B，C，n，m五个参数均为常数，由实验测定，A为屈服应力，B为应变硬化系数，C为应变率相关系数，n为应变硬化指数，m为温度相关系数；T*为无量纲温度，可表示为

(6)

式中：Troom为参考温度；Tmelt为材料的熔化温度(熔点)。

由于理论计算特别复杂，本文采用LS-DYNA有限元法，进行电磁-温度-结构等多物理场耦合数值模拟，为研究均匀线圈轴向脉冲磁场对粗细不均匀金属射流的作用机理，假设金属射流为轴对称、无旋转的塑性连续体，同时假定金属射流为无限长且处于劲缩状态，故可不考虑金属射流轴向速度，取一个金属射流微元进行研究。

2 数值模拟

2.1 物理模型及验证

约束金属射流所需磁场由励磁线圈提供，励磁线圈采用螺线管线圈，螺线管长度为50 mm，内径为10 mm，螺线管所用绕线截面为正方形，边长为4 mm；金属射流采用变截面圆杆，长度为20 mm，最大直径为5 mm，最小直径为2 mm，外形轮廓线复合正弦曲线，用来模拟金属射流劲缩部分，网格剖分如图3所示；螺线管线圈中施加脉冲电流幅值为50 kA，脉宽为25 μs，加载脉冲电流如图4所示；线圈和金属射流材料均为铜；金属射流材料参数如表1。表1中，E为杨氏弹性模量，G为切变模量，Pr为泊松比，ρ0为密度，其他参数为金属射流材料的本构模型参数。

表1 金属射流材料参数

这里采用理论分析与数值模拟结果对比的方法，验证数值计算方法的可行性和正确性。通过金属射流9681号单元在t=5 μs时数值模拟得到的电磁场分布数据与理论计算结果进行对比验证，数值模拟结果为：感应电流密度j=4.42×1 010 A/m2，磁感应强度B=8.81 T，电磁力密度dF/dV=3.9×1011N/m3。根据电磁感应原理，金属射流电磁力密度可表示为j×B=3.894×1011N/m3≈dF/dV，由此可得，数值模拟结果和理论计算结果一致，故该数值仿真计算方法可用于分析励磁线圈磁场约束金属射流变形的作用机理分析。

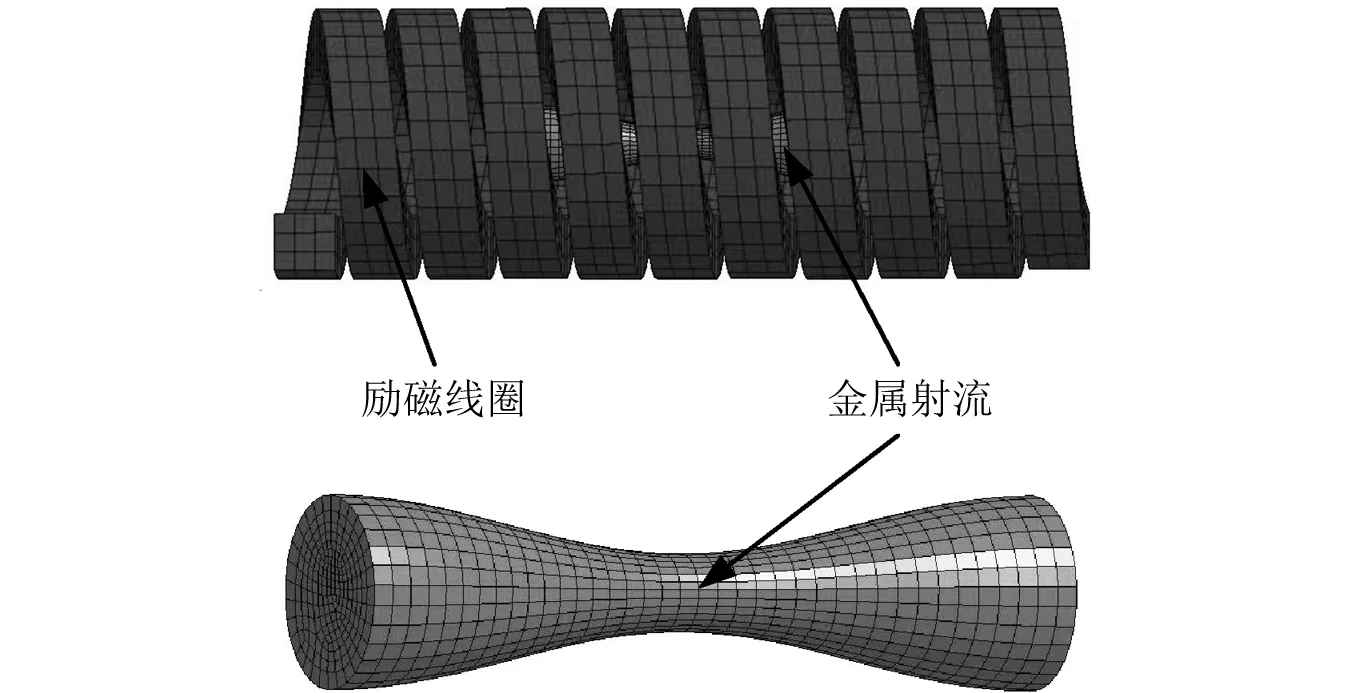
图3 励磁线圈和金属射流三维网格剖分Fig.3 The 3D cross-section model of magnet exciting coil and SCJ

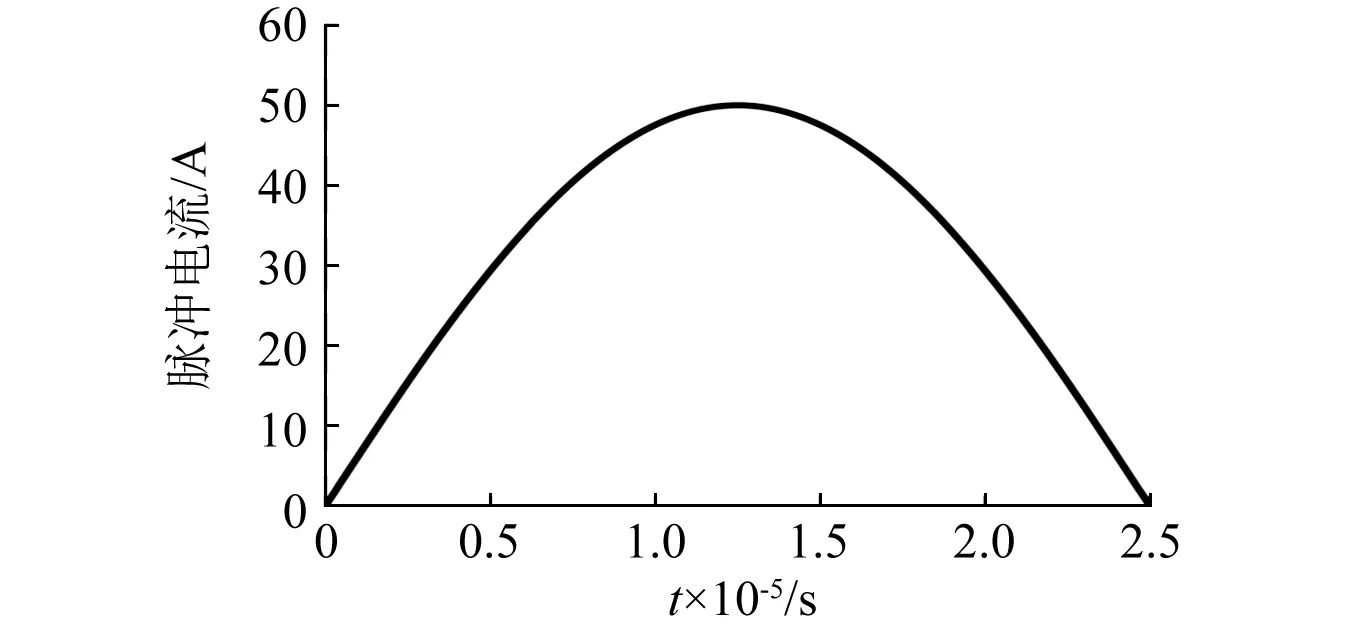
图4 励磁线圈加载脉冲电流曲线Fig.4 Curve of current through the coil

2.2 结果及分析

2.2.1 电磁场分析

图5为13 μs时金属射流中感应电流密度分布云图，图5(a)表示感应电流密度大小，图5(b)主要表示感应电流密度方向。

由图5(a)分析得知，在金属射流表面，感应电流密度沿轴向呈梯度分布，由凸起部分到凹陷部分逐渐减小，凸起部分达到2.107×1010A/m2，凹陷部分为1.405×1010A/m2；在金属射流内部，感应电流密度呈现一定程度的趋肤效应，主要集中在金属射流表面，在同一半径方向，感应电流密度呈梯度分布，由金属射流表面到中心逐渐减小，中心部分对应值为1.631×106A/m2。

图5(b)表明，感应电流密度方向与励磁线圈中脉冲电流变化密切相关，金属射流中由表面到内部，感应电流密度均呈现切向涡旋状，且方向正好与励磁线圈中施加脉冲电流方向相反，即感应电流所产生的磁场会阻碍励磁线圈内部的磁通量增加。

图5 金属射流中感应电流密度分布Fig.5 Distribution of induced current density of SCJ

图6为金属射流中表面感应电流密度随时间的变化规律。由图可以看出，凸起部分感应电流密度整体大于凹陷部分，引起这种分布规律的原因为：金属射流凸起部分首先对励磁线圈磁场变化做出反应，且凸起部分距离励磁线圈内表面较近，故感应电流密度较大。同时可以看出，感应电流密度的变化周期要滞后于励磁线圈中脉冲电流的变化，励磁线圈中脉冲电流变化率方向发生变化的时刻为t=12.5 μs，感应电流密度发生反向的时刻为t=17.5 μs和t=20 μs，这主要是由感应电流的惯性效应引起的，即金属射流中感应电流密度方向不会发生突变。

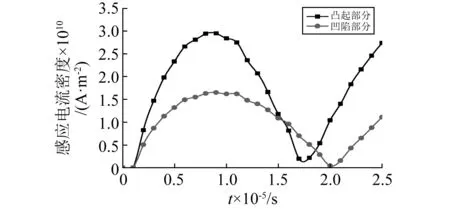
图6 金属射流表面感应电流密度随时间的变化规律Fig.6 Variation law with time of induced current density of SCJ

图7为13 μs时金属射流中磁感应强度分布云图，图7(a)表示磁感应强度大小，图7(b)主要表示磁感应强度方向。可以看出，金属射流凸起部分的磁感应强度大于凹陷部分，且表面磁感应强度大于内部，这种分布规律主要由磁场趋肤效应引起，励磁线圈磁场在电流上升期内来不及扩散到金属射流内部。同时金属射流表面磁感应强度梯度分布不如感应电流明显，这主要是因为金属射流直径越大，感应电流形成的磁场对励磁线圈的抵消作用越强。由图7(b)可以看出，磁感应强度矢量方向与金属射流外形平行，由金属射流一端指向另一端。

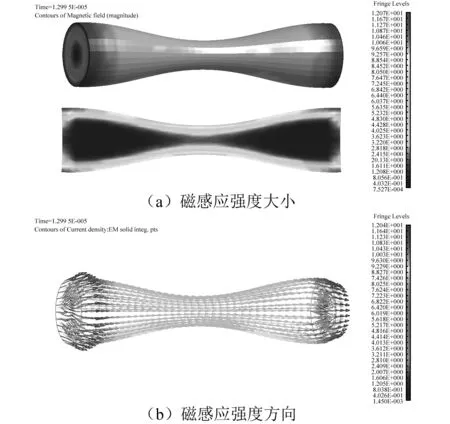
图7 金属射流中磁感应强度分布Fig.7 Distribution of magnetic flux intensity of SCJ

图8为金属射流中磁感应强度随时间的变化规律。凸起部分的磁感应强度整体大于凹陷部分，磁感应强度的变化周期与励磁线圈中脉冲电流的变化周期一致，主要是因为金属射流中感应电流所产生的磁场阻碍励磁线圈磁场的变化，其抵消作用较弱，金属射流中的磁场主要是由励磁线圈脉冲电流产生的磁场。当t=15 μs时，凸起部分和凹陷部分磁感应强度均达到最大值，对应值分别为12.30 T和9.88 T。

图8 金属射流中磁感应强度随时间的变化规律Fig.8 Variation law with time of magnetic flux intensity of SCJ

图9为13 μs金属射流中电磁力密度分布云图。图9(a)表示电磁力密度大小，图9(b)表示电磁力密度方向。与感应电流密度和磁感应强度分布类似，电磁力密度呈现凸起部分较大、凹陷部分较小的现象，且表现出更强的趋肤效应。由理论分析和前文相关分析可知，电磁力密度由感应电流密度和磁感应强度决定，其中感应电流密度起主要作用。由图9(b)可以得出，电磁力由金属射流表面指向内部，电磁力密度、感应电流密度及磁感应强度三个矢量符合右手定则。

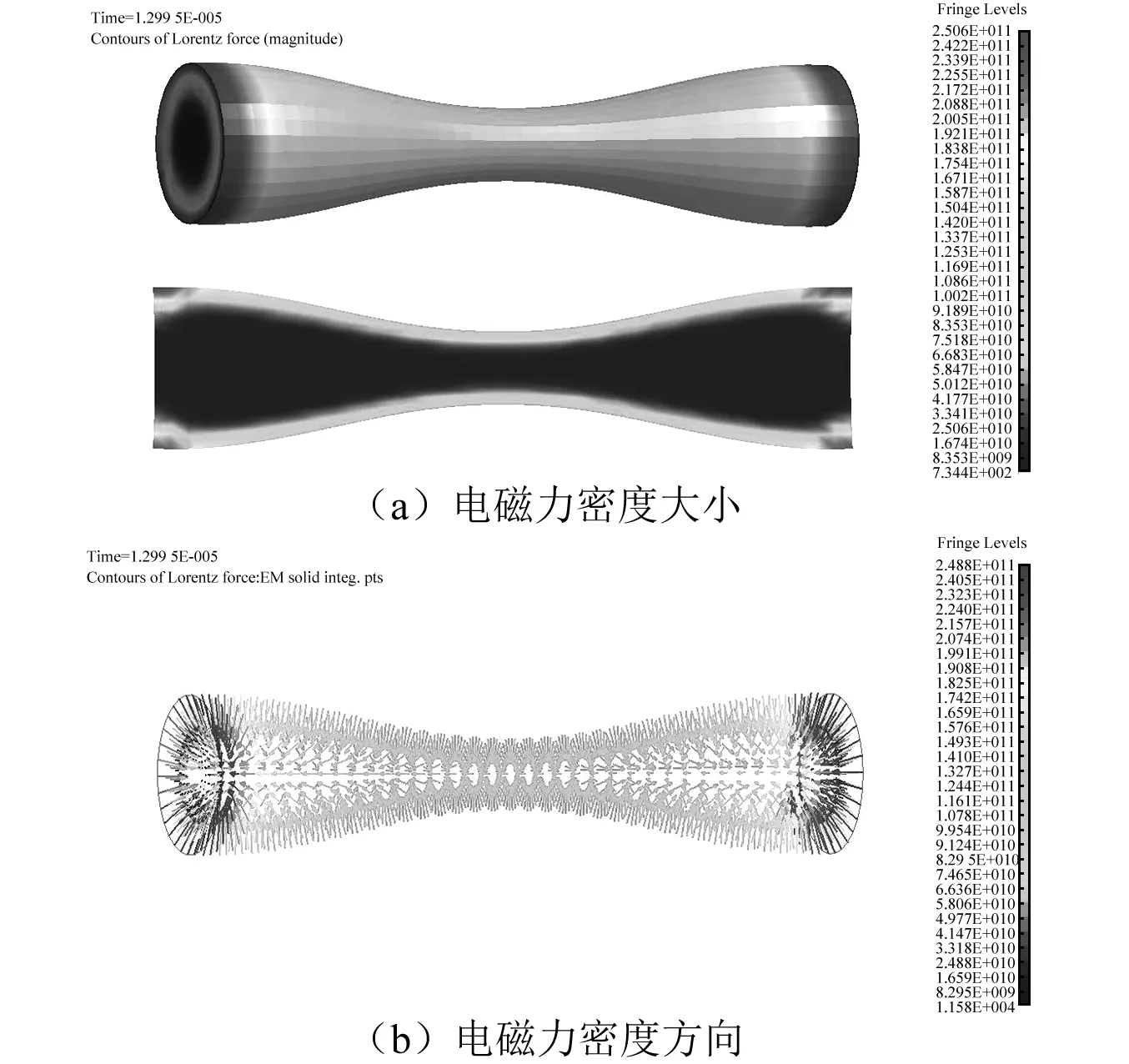
图9 金属射流中电磁力密度分布Fig.9 Distribution of electromagnetic force density of SCJ

图10为金属射流中电磁力密度随时间的变化规律。电磁力密度出现两个峰值，其中第一个峰值范围内的电磁力密度是引起金属射流发生箍缩变形的主要原因，而第二个峰值范围内的电磁力密度由于已经发生反向，故其不利于金属射流箍缩变形发展。进一步分析得知，第二个峰值范围内的电磁力密度已经发生反向，而这种反向首先出现在金属射流表面，而后不断向内部发展，即金属射流表面和内部电磁力密度方向相反直至完全反向的阶段，这主要是由金属射流中感应电流密度的反趋肤效应引起的。

图10 金属射流中电磁力密度随时间的变化规律Fig.10 Variation law with time of electromagnetic force density of SCJ

2.2.2 温度场分析

图11为金属射流中温度分布云图。可以看出，金属射流表面温度凸起部分较大，凹陷部分较小，温度最大值集中在凸起部分直径最大处附近；同时，温度也呈现很强的趋肤效应，表面温度最大值为1 130 K，而内部温度为1 098 K。这种温度分布现象主要由金属射流中所产生感应电流的热效应引起，感应电流主要集中在金属射流表面，导致金属射流表面温升较快；由前文分析得知，感应电流扩散到金属射流内部需要一定时间，故内部温度基本没有变化。

图11 金属射流中温度场分布Fig.11 Distribution of temperature field of SCJ

图12为金属射流中温度随时间的变化规律。结果显示，金属射流凸起部分和凹陷部分温度均随时间增大而升高，但凸起部分温升明显高于凹陷部分温升，凸起部分温升为39 K，凹陷部分温升为14 K。温度升高会引起金属射流材料的等效流动极限降低，进而使金属射流软化，在电磁力作用下更容易发生变形，由于凸起部分温升始终高于凹陷部分，可以推测金属射流凸起部分的变形量要明显高于凹陷部分。

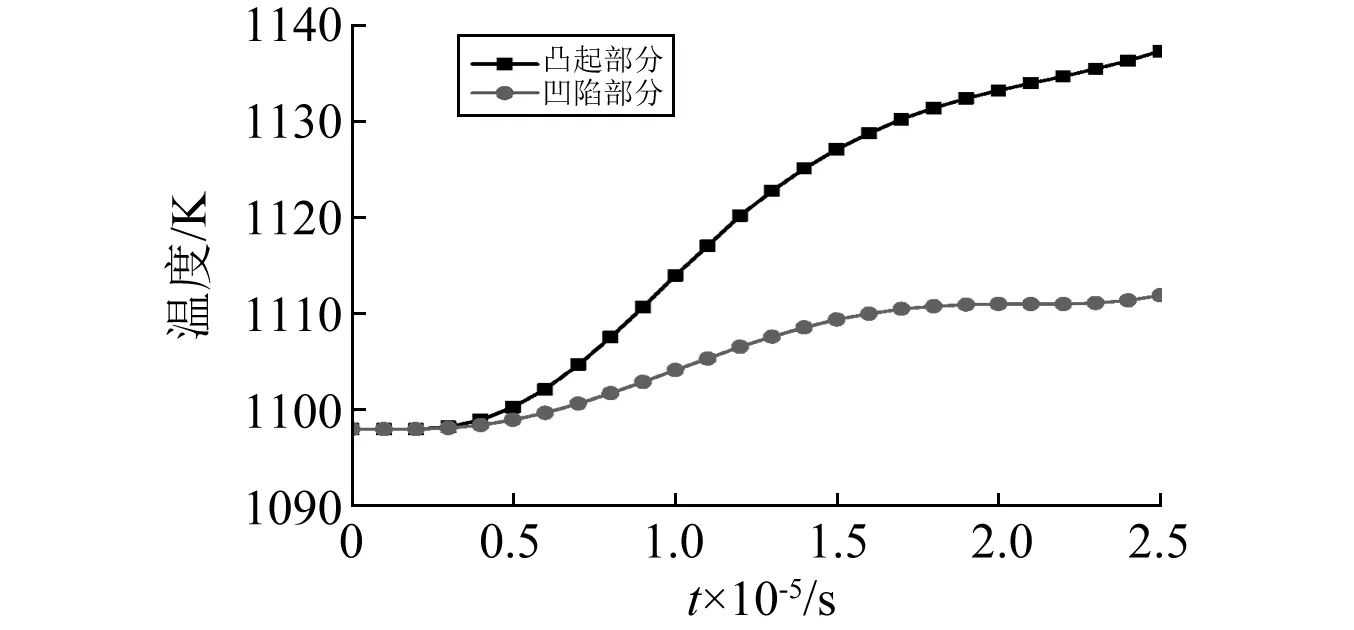
图12 金属射流中温度随时间的变化规律Fig.12 Variation law with time of temperature of SCJ

图13为金属射流中欧姆热功率分布云图。结果显示，凸起部分欧姆热功率明显大于凹陷部分，在金属射流径向，表面欧姆热功率明显大于内部。欧姆热在金属射流凸起部分的积聚，会直接引起金属射流进一步软化，在励磁线圈所产生电磁力的作用下，由表面向内部逐渐压缩，进而减小金属射流劲缩部分的直径差，延缓其断裂过程。

图13 金属射流中欧姆热功率分布Fig.13 Distribution of ohmic heating power of SCJ

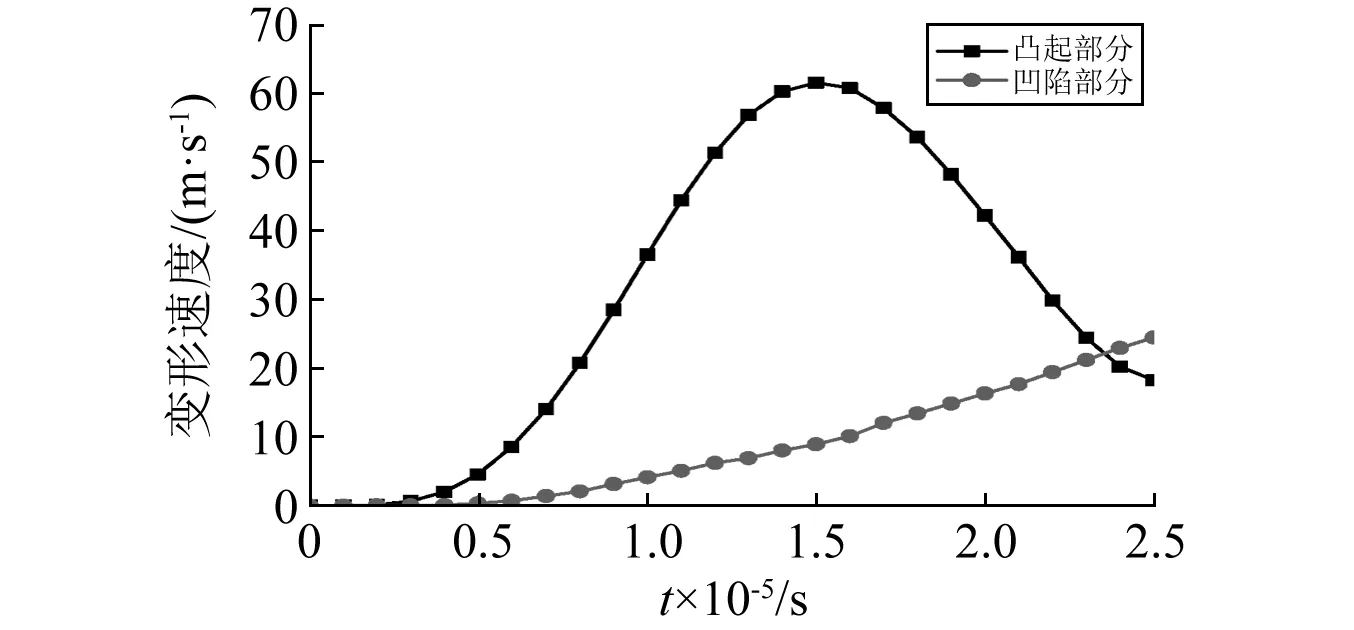
图14为金属射流中欧姆热功率随时间的变化规律。结果显示，凸起部分欧姆热功率在任意时刻均大于凹陷部分，且二者差距较大，欧姆热功率对时间的积分可以得到金属射流中的欧姆热总量，可用图中欧姆热功率曲线所包围的面积来衡量，可以看出，凸起部分欧姆热总量明显大于凹陷部分，一方面使得凸起部分金属射流材料更加软化，另一方面凸起部分所受电磁力较大，两种因素共同促进凸起部分发生较大变形，最终使得金属射流整体趋向更加均匀。

图14 金属射流中欧姆热功率随时间的变化规律Fig.14 Variation law with time of ohmic heating power of SCJ

2.2.3 结构场分析

图15为金属射流中有效应力分布云图。结果显示，凸起部分和凹陷部分之间靠近金属射流表面的区域以及凹陷部分有效应力较大。依据前文分析可知，金属射流凸起部分所受电磁力相对较大，而有效应力较大区域并未出现在凸起部分直径最大处，分析可得，金属射流材料不仅发生径向变形，同时在电磁力作用下也发生轴向变形，这种轴向变形会引起金属射流材料流动，进而有效应力呈现图中所示状态。

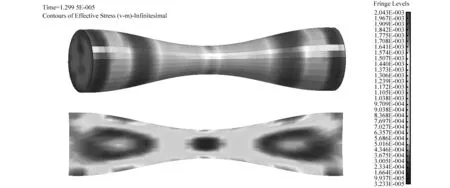
图15 金属射流中有效应力分布Fig.15 Distribution of effective stress of SCJ

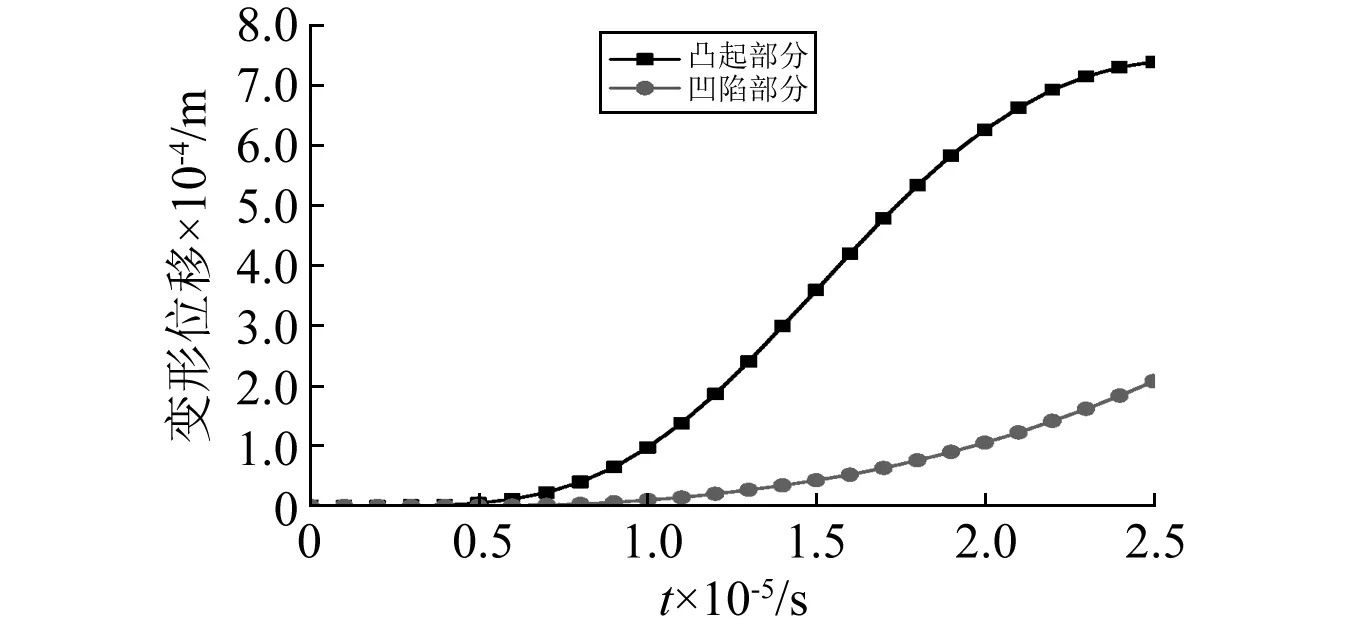
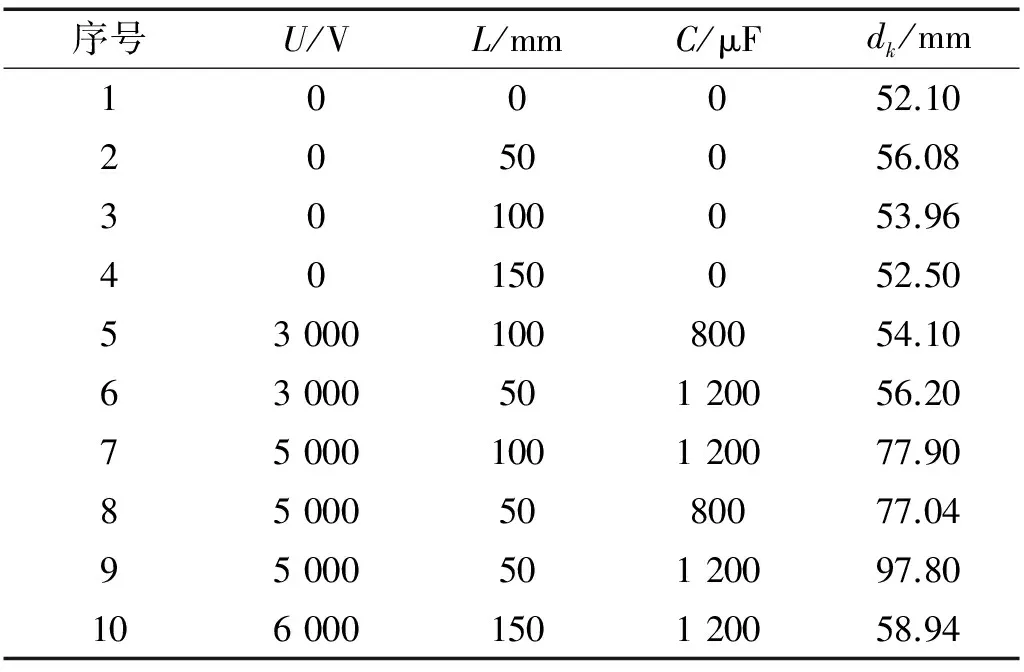
图16为金属射流中有效应力随时间的变化规律。当t<15 μs和22 μs

图16 金属射流中有效应力随时间的变化规律Fig.16 Variation law with time of effective stress of SCJ

图17为金属射流中有效应变分布云图。结果显示，有效应变分布规律与前文所述有效应力分布规律相似，这种分布规律主要由理论分析部分所描述的金属射流材料的应力和应变关系所决定。

图17 金属射流中有效应变分布Fig.17 Distribution of effective strain of SCJ

图18为金属射流中有效应变随时间的变化规律。由图可以看出，凸起部分有效变形起始时刻为t=15 μs，随着时间推移，凸起部分有效变形逐渐增大，当23 μs

图18 金属射流中有效应变随时间的变化规律Fig.18 Variation law with time of effective strain of SCJ

图19为金属射流中材料变形速度分布云图。结果显示，凸起部分变形速度明显大于凹陷部分，凸起部分直径最大处变形速度最大。金属射流材料变形速度主要由其所受电磁力和材料温度所决定，根据前文分析得知，凸起部分所受电磁力及材料温升均大于凹陷部分，电磁能提供的驱动力和欧姆热聚积引起的材料软化，共同致使金属射流凸起部分变形速度明显大于凹陷部分。

图19 金属射流中材料变形速度分布Fig.19 Distribution of deformation velocity of SCJ

图20为金属射流中材料变形速度随时间的变化规律。结果显示，凸起部分材料变形速度呈现先增大后减小的规律，凹陷部分材料变形速度呈现逐渐增大的规律。凸起部分材料变形速度在t=15 μs时达到最大，而此刻对应的电磁力并不大，进一步说明材料变形所需能量来自电磁力做功和欧姆热的积累；凹陷部分材料变形速度同时受电磁力和材料流动力二者共同作用，由于凹陷部分所受电磁力较小，故材料流动力起主导作用，其变形速度在一直上升。

图20 金属射流中材料变形速度随时间的变化规律Fig.20 Variation law with time of deformation velocity of SCJ

图21为金属射流变形位移的分布云图。结果显示，变形位移分布规律与变形速度相似，凸起部分变形位移明显大于凹陷部分，凸起部分直径最大处变形位移最大，变形位移是变形速度对时间累积的效果。

图21 金属射流变形位移的分布Fig.21 Distribution of deformation displacement of SCJ

图22为金属射流变形位移随时间的变化规律。由图可以看出，凸起部分和凹陷部分变形位移均随时间推移而不断增大，凸起部分变形位移明显大于凹陷部分。当t=25 μs时，凸起部分的变形位移为0.739 mm，凹陷部分的对应值为0.208 mm。进一步分析得知，凸起部分累积所受电磁力明显大于凹陷部分，电磁力对凸起部分所做的功远大于凹陷部分，同时凸起部分欧姆热累积较多，材料软化较明显，故引起凸起部分变形位移明显大于凹陷部分，最终使得金属射流整体更加均匀。

图22 金属射流变形位移随时间的变化规律Fig.22 Variation law with time of deformation displacement of SCJ

图23为金属射流在t=0 μs，20 μs和24 μs时对应的变形情况。可以看出，随着时间推移，金属射流凸起部分直径逐渐减小，凹陷部分直径逐渐增加，使得凸起部分和凹陷部分直径差减小，金属射流整体更加均匀。根据前文分析可以总结得出，金属射流发生有效变形的能量主要来自励磁线圈施加到金属射流上的电磁力做功和感应电流引起的欧姆热效应，且要保证金属射流发生有效变形，需要电磁力做功和欧姆热不断累积，即励磁线圈中脉冲电流要保持一定脉宽，以保证金属变形所需的作用动量。

图23 金属射流在t=0 μs，20 μs和24 μs时对应的变形情况Fig.23 Deformation of SCJ when t=0 μs, 20 μs and 24 μs

3 试验验证

前文主要通过理论分析和数值模拟相结合的方式探究了励磁线圈磁场约束金属射流变形的作用机理，为保证研究完备性，进行了相关验证试验，通过分析励磁线圈磁场作用下金属射流对目标靶板的侵彻穿深变化，验证了励磁线圈磁场约束金属射流变形的作用机理。励磁线圈磁场约束金属射流变形的验证试验系统如图24所示，主要由充放电子系统、破甲弹子系统、测量子系统及控制子系统组成。充放电子系统包括充电电源模块、螺线管式励磁线圈及脉冲储能电容器组等，通过充电电源为脉冲储能电容器组充电，脉冲电容器组经过励磁线圈放电进而产生强磁场，为约束金属射流变形提供电磁驱动力；破甲弹子系统主要为破甲弹本体，雷管起爆聚能装药，进而压垮药型罩产生金属射流；测量子系统包括电压测量装置和电流测量装置，用于监测试验过程中励磁线圈电参数和三电极间隙开关电参数变化；控制子系统包括总控制开关、三电极间隙开关及延时控制开关，总控制开关用于产生同一触发信号，确定时间原点，三电极间隙开关用于控制主放电回路，确定放电延时时间，延时控制开关用于控制雷管延时起爆时间，最终确定金属射流产生与励磁线圈磁场建立之间的时序。主放电回路与控制回路之间的时序如图25所示。

图24 励磁线圈磁场约束金属射流试验系统Fig.24 Experiment system of SCJ restricted by magnetic field of magnet exciting coil

图25 主回路与控制回路时序测量Fig.25 Time sequence of main circuit and controlled circuit

表2 试验原始数据

基于正交试验法和对比试验法，共开展了10次实弹试验，已说明不同参数条件对金属射流作用效果的影响，试验设计及结果如表2所示，表中U、L、C、dk分别表示脉冲储能电容器组充电电压、励磁线圈长度、电容器组电容及金属射流对目标靶板的侵彻穿深。1～4号试验分析无励磁线圈磁场作用下，励磁线圈长度对金属射流侵彻穿深能力的影响，结果表明，励磁线圈长度越长，金属射流对目标的侵彻穿深能力越弱。第8号试验金属射流在励磁线圈磁场作用下对目标靶板的侵彻穿深及残留杵体外形如图26所示，将杵体部分放大分析可得，杵体外形与无磁场作用时相比较光滑，进一步表明励磁线圈磁场对金属射流变形过程的控制作用。

图26 第8号试验后效靶板穿深及杵体Fig.26 Aftereffect target and plug of the eighth experiment

在进行对比试验分析时，2号、6号、8号为对比组，3号、5号、7号为对比组，4号、10号为对比组，三个对比组分别以2号、3号、4号试验为参考，6号、8号、5号、7号、10号试验结果中金属射流对目标靶板的侵彻穿深增量分别为0.2%、37.4%、0.3%、44.4%、12.3%。结果表明，励磁线圈磁场可对金属射流进行有效约束，控制金属射流变形过程，减小金属射流颈缩部位直径差；随着脉冲储能电容器组充电电压升高，金属射流对目标靶板的侵彻穿深增量增大，当充电电压为3 kV时，励磁线圈脉冲电流为39.42 kA，对应的金属射流对目标靶板的侵彻穿深增量很小，说明励磁线圈磁场较弱，其对金属射流施加的电磁力较小，金属射流变形不明显；当充电电压为5 kV时，励磁线圈脉冲电流为68.39 kA，对应的金属射流对目标靶板的侵彻穿深增量较大，说明励磁线圈磁场对金属射流施加的电磁驱动力导致其发生有效变形；当充电电压为6 kV时，励磁线圈脉冲电流为118.67 kA，对应的金属射流对目标靶板的侵彻穿深增量反而小于5 000 V的对应增量，这是由于励磁线圈长度增加引起试验系统电感和电阻增大，励磁线圈磁场因此减弱，对金属射流变形过程控制作用降低。

表1中，5～8号试验为正交试验组，根据正交试验法进行分析，可得到不同因素水平对金属射流侵彻穿深能力的影响程度。结果表明，对金属射流侵彻穿深能力影响程度大小的因素依次为脉冲储能电容器充电电压、电容和励磁线圈长度，由正交分析可知，最佳参数组合为5 000 V、50 mm、1 200 μF，故在该参数条件下进行试验，对应的金属射流对目标靶板的侵彻穿深为97.80 mm，以2号试验为参考，其侵彻穿深增量为74.4%，进一步验证了励磁线圈磁场对金属射流变形过程的约束作用。

4 结 论

(1)励磁线圈磁场能够对破甲弹金属射流进行有效约束，使金属射流发生有效变形，减小金属射流直径差，使其整体更加均匀，延缓其局部变细至断裂的过程。

(2)在励磁线圈脉冲磁场作用下，金属射流凸起部分的感应电流密度、磁感应强度及电磁力密度均大于凹陷部分的对应值，三者均呈现出较强的趋肤效应。金属射流凸起部分和凹陷部分的电磁力差是引起金属射流发生变形的直接因素。

(3)金属射流在感应电流热效应的影响下温度会不断升高，引起欧姆热不断累积，导致金属射流材料的等效流动极限降低，进而使金属射流软化，在电磁力作用下金属射流更容易发生变形。

(4)励磁线圈磁场对金属射流施加的电磁力和金属射流中感应电流累积引起的材料软化共同导致金属射流发生有效变形，其中电磁力对金属射流变形起到决定性作用，为使得金属射流发生有效变形所需要的作用动量，励磁线圈脉冲电流需要达到一定峰值和脉宽。

(5)试验分析相关结果表明，励磁线圈磁场可有效控制金属射流变形过程，进而增强其对目标的毁伤效果。脉冲储能电容器充电电压、电容及励磁线圈长度可影响金属射流变形过程，影响程度由大到小依次为脉冲储能电容器充电电压、电容及励磁线圈长度，进一步说明电参数对金属射流作用效果的影响要大于结构参数的影响，随着脉冲储能电容器充电电压和电容增大，金属射流对目标的毁伤效果逐渐增强，励磁线圈长度需要控制在破甲弹有效炸高范围内，以保证金属射流变形所需的磁场强度。

[ 1 ] 陈闯 ，王晓鸣，李文彬，等. 爆轰波波形与药型罩结构匹配对杆式射流成形的影响[J]. 爆炸与冲击，2015,35(6): 812-819.

CHEN Chuang, WANG Xiaoming, LI Wenbin, et al. Effect of matching of detonation waveform with liner configuration on the rod-like jet formation[J]. Explosion and Shock Waves, 2015, 35(6): 812-819.

[ 2 ] KARLSSON H. Computer simulation of shaped charge jet fragmentation[C]∥The 19th International Symposium on Ballistics. Interlaken：ISB, 2001: 819-826.

[ 3 ] HORSFALL I, PETROU E, CHAMPION S M. Shaped charge attack of spaced and composite armour[C]∥ The 23th International Symposium on Ballistics. Tarragona: ISB, 2007: 1281-1288.

[ 4 ] SHVETSOV G A, MATROSOV A D, FEDOROV S V, et al. Electromagnetic control of the shaped-charge effect[J]. The 19th International Symposium of Ballistics, Interlaken, Switzerland, 2001, 5:851-857.

[ 5 ] SHVETSOV G A, MATROSOV A D. Qualitative physical model for the disruption of shaped-charge jets by a current pulse[C]∥ The 20th International Symposium on Ballistics. Orlandol:ISB, 2002: 613-619.

[ 6 ] SHVETSOV G A, MATROSOV A D, FEDOROV S V, et al. Effect of external magnetic fields on shaped-charge operation[J]. International Journal of Impact Engineering, 2011,38(6):521-526.

[ 7 ] FEDOROV S V, BABKIN A V, LADOV S V, et al. Magnetic armor as a method of anti-terror protection of objects against shaped-charge action[C]∥The 23th International Symposium on Ballistics. Tarragona:ISB, 2007: 1091-1098.

[ 8 ] FEDOROV S V. Magnetic stabilization of elongation of metal shaped charge jets[C]∥The 25th International Symposium on Ballistics. Beijing:ISB, 2010: 967-975.

[ 9 ] FEDOROV S V, LADOV S V. Powerful electric discharge as method of anti-shaped-charge protection[C]∥ The 27th International Symposium on Ballistics. Freiburg:ISB, 2013: 1723-1734.

[10] GRACE F, DEGNAN J, ROTH C, et al. Shaped charge jets driven by electromagnetic energy[C]∥ The 28th International Symposium on Ballistics. Atlanta:ISB, 2014: 15-26.

[11] 俎栋林. 电动力学[M].北京：清华大学出版社, 2006:111-117.

[12] 孙承纬. 爆炸物理学[M].北京: 科学出版社, 2011:1048-1061.

[13] 雷彬，李鹤，李军，等. 电磁轨道炮发射过程的轨道变形研究[J]. 振动与冲击，2014, 33(3): 182-185.

LEI Bin, LI He, LI Jun, et al. Rail deformation during launching of an electromagnetic railgun[J]. Journal of Vibration and Shock, 2014, 33(3): 182-185.

[14] 夏明，黄正祥，顾晓辉，等. 磁爆加载初始阶段薄壁金属管冲击变形研究[J]. 振动与冲击，2012, 31(14): 7-10.

XIA Ming, HUANG Zhengxiang, GU Xiaohui, et al. Shock-produced deformation of a thin-walled metal tube subjected to magnetic load caused by FCG in initial stage[J]. Journal of Vibration and Shock, 2012, 31(14): 7-10.