结构不等间距布置对圆柱壳结构声学性能的影响

谭 路， 纪 刚， 周其斗， 张纬康

(海军工程大学 舰船工程系，武汉 430033)

加肋圆柱壳、分舱圆柱壳是航天工程与海洋工程领域常见结构[1]，圆柱壳的肋骨与舱壁设通常计为等间距布置形式，其主要考虑了壳体强度与设计、施工的难度，但未从改善圆柱壳结构声学性能的角度加以考虑。等间距结构的振动特性表现为在频域上交替存在通带与止带，虽然在止带频段结构振动的衰减较大，但在通带频段结构振动却较大，于减振降噪不利[2]。因此，通过研究新的结构布置形式——不等间距结构布置形式——对壳体结构振动的影响规律，可为优化圆柱壳结构声学性能提供指导，对工程实际具有重要意义。

目前，不等间距结构的振动特性研究并未引起足够的重视，相关文献较少，多集中于上世纪八十年代至本世纪初，主要由国外Hodges等[3-8]开展，这些研究以解析法为主要计算方法，重点对一维不规则耦合振子系统[9-10]、一维不等间距梁结构[11-12]、二维不等间距加肋板[13-14]等简单结构的振动特性进行了研究。这些研究得出的主要结论有三点：①不等间距结构振动具有安德森定域效应(Aderson Localization)，即在通带内，相比结构波能在等间距结构上自由传播，不等间距结构上结构波的幅值随着远离激励源成指数衰减，结构的振动能量聚集在激励源附近[15-16]；②将结构离散成首尾相连间距不一的子结构，安德森定域效应受子结构不规则程度与子结构间耦合强度比值的影响，若仅改变各子结构的不规则程度，则不规则程度越大，安德森定域效应越强[17-18]；③安德森定域效应受不等间距结构维度影响较大，随着维度升高，安德森定域效应减弱，对给定子结构耦合强度的三维不等间距结构，存在结构不规则程度的阈值，仅当结构不规则程度达到阈值后，结构才会显现出安德森定域效应现象[19-20]。上述文献虽然得出了一些有益的结论，但关于结构不等间距布置对圆柱壳结构声学性能影响的研究较少，且并未从物理意义上解释清楚结构不等间距布置影响圆柱壳结构声学性能的机理。

本文以不等间距加肋圆柱壳作为研究对象，以等间距加肋圆柱壳为对比模型，采用有限元方法计算获得壳体振动响应，以此为输入获得壳体均方法向速度级声学传递函数。同时以壳体振动响应为输入，通过波数谱分析方法[21]将其分解为各简谐波分量的叠加，得到各振动分量的法向速度振动功率波数谱。通过对两模型的均方法向速度级声学传递函数与波数谱的分析，总结获得结构不等间距布置对圆柱壳结构声学性能的影响规律及其机理。其中有限元法、结构声学传递函数理论不再赘述，重点对波数谱分析理论进行推导，并通过一维不等间距梁结构振动理论介绍安德森定域效应产生的机理。

1 圆柱壳的波数谱分析理论

通过有限元方法计算获得圆柱壳在激励作用下的振动响应，以此为输入利用波数谱分析方法对壳体的振动响应进行波数谱分析。假设圆柱壳两端存在无限长柱屏，壳体振动响应可表示为

(1)

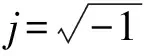
(2)

将式(1)中的法向位移的平方在圆柱壳表面上积分，可得壳体的法向速度振动功率

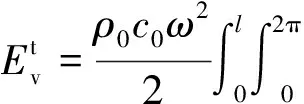
(3)

式中：ρ0、c0分别为耦合流体的密度与声速，本文中的耦合流体均指空气；a为圆柱壳半径。联立式(2)与式(3)，简化可得

(4)

由于总的法向速度振动功率也可表示为各波数为(n,kx)的波分量的法向速度振动功率的叠加，因此根据式(4)可得出法向速度振动功率谱Ev(n,kx)

(5)

周向波数为n的所有结构波的法向速度振动功率为

(6)

2 安德森定域效应机理分析

对一维无阻尼单支座简支支撑梁结构，若在支座处入射波表示为ejkx，则透射波与反射波可分别表示为tejkx与re-jkx，其中t、r分别为透射与反射系数。

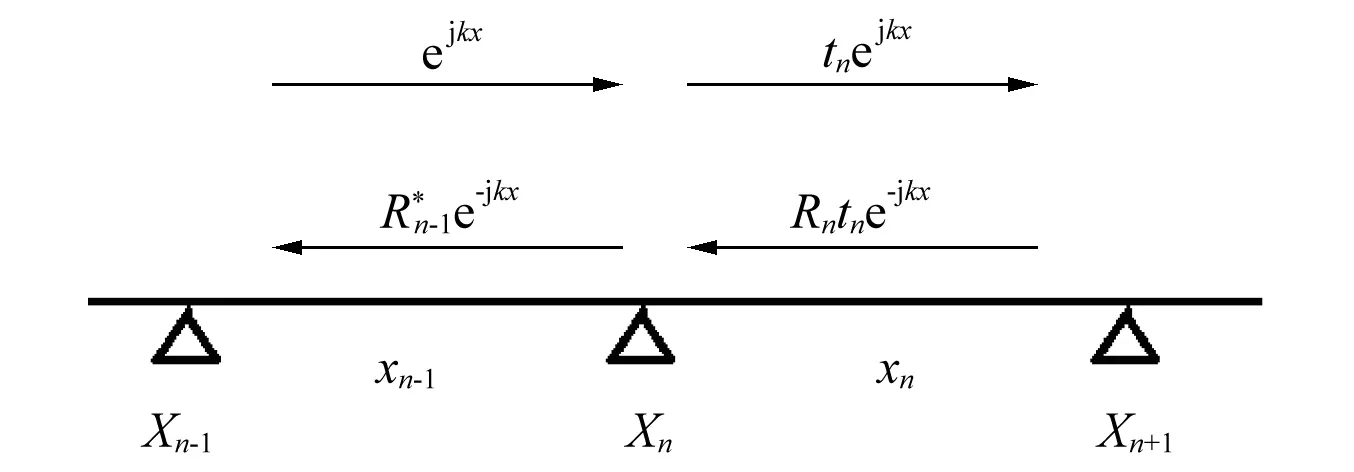
图1 无限长多跨度简支支撑梁示意图Fig.1 Multi span simply surported infinite beam

结合单支座梁的结构波散射关系，对上述多支座梁的结构波入射、透射、反射关系进行重整，有[22]

(7)

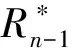
若结构波传递经过N个支座，则总传递系数为TN

(8)

对总传递系数取对数可得

(9)

式中，由于|r|<1，|Rn|≤1，因此上式第二项可按照等比级数展开。

若不等见距支撑梁的支座间距为随机分布，则重整后反射系数间的相位因子也为随机分布，使得Rn关于n的值在|Rn|≤1范围内同样为随机分布，因此式(9)可化为

Nlnt+O(N1/2)

(10)

由式(10)可知，随着结构波传播经过支座数N的增加，总传递系数TN减小，结构波不能在该结构上自由传播，其幅值随传播距离的增加成指数衰减，即结构振动主要聚集在激励源附近，显现了结构振动的安德森定域效应现象。

相比等间距结构在通带时结构波能自由传播，不等间距结构波传播具有较大衰减，显现安德森定域效应的物理机理在于：支座(或构件)的不等间距布置，使得结构波不再满足弗洛德条件[23]，即破坏了结构波在各支座位置处的相位匹配关系，使得支座对结构波的反射作用增强，传播衰减增大。

3 不等间距加肋圆柱壳轴向波数谱分析

以周向n=0阶的振动模式为例，对等间距与不等间距加肋圆柱壳轴向的振动特性进行分析。圆柱壳壳厚6 mm，舱壁厚30 mm，肋骨厚20 mm，高300 mm。等间距加肋圆柱壳的肋骨间距均为600 mm，不等间距加肋圆柱的肋骨布置形式如图2所示。两模型全部采用钢材料，其杨氏模量为2.05×105N/mm2，密度为7.80×10-6kg/mm3，泊松比为0.3。为方便对不等间距结构振动特性进行机理研究，该模型肋骨厚度并不随肋间距改变而变化。

图2 不等间距加肋圆柱壳结构示意图Fig.2 Aperiodic ribbed cylindrical shell

建立圆柱壳的结构有限元模型。两模型均采用四边形单元建立，具有相同的单元数，均有单元49 408个，节点49 410个，其中单元尺度为50 mm，即等间距加肋圆柱壳肋间轴向划分为12个单元。对本文最高计算频率而言，符合最短结构波由6个单元描述的条件，满足计算精度要求。图3为不等间距加肋圆柱壳结构有限元模型的纵剖图。

为方便分析，在圆柱壳左端施加环形均匀的径向简谐激励，激励幅值为1 N，见图1。计算时模型采用自由边界条件。此时，圆柱壳振动以周向n=0阶的振动模式为主。

图4为等间距与不等间距加肋圆柱壳壳体的均方法向速度级声学传递函数频率曲线，它描述了激振力幅值为1 N时壳体响应的均方法向速度级随频率的变化关系，易见：①两模型的均方法向速度级声学传递函数在低频时相似，在中高频有较大区别，其物理机理为，低频时结构波长较长，肋骨布置形式对壳体总振动影响较小，随着频率增高，结构波长变短，肋骨布置形式对壳体振动的影响才体现出来；由此可以推论，由于舱壁之间布置间距较大，舱壁布置形式将对更低频段壳体振动产生影响；②由等间距加肋圆柱壳振形可知，390 Hz以上的谱峰频段均为其通带，在各通带处，肋骨间距均为轴向结构波半波长的整数倍，(图中已标记出肋骨间距与各通带处壳体振动主要结构波长的比值)，在该系列通带处，不等间距加肋圆柱壳的传递函数值相对有较大降低，表明其振动相对等间距加肋圆柱壳具有较大衰减，显现了安德森定域效应现象；③在等间距圆柱壳的止带，不等间距圆柱壳的均方法向速度级传递函数较大，不等间距加肋圆柱壳振动强于等间距加肋圆柱壳。

图4 等间距与不等间距加肋圆柱壳均方法向速度级声学传递函数频率曲线Fig.4 Mean square velocity level transmission function of periodic and aperiodic ribbed cylindrical shells

以等间距加肋圆柱壳的谱峰频率391 Hz、637 Hz、862 Hz及波谷频率544 Hz为例，对两圆柱壳的轴向振动进行波数谱分析。由于壳体法向速度振动功率波数谱描述了不同波数成分结构波对壳体总振动贡献的大小，因此，通过对壳体法向速度振动功率波数谱的分析，可直观的从机理上理解等间距与不等间距加肋圆柱壳结构声学性能不同的原因。

图5为等间距与不等间距加肋圆柱壳在典型频率处周向为n=0阶的法向速度振动功率波数谱，其中壳体轴向无因次波数为12lkx/π。易见：①对谱峰频率391 Hz、637 Hz、862 Hz，两曲线随波数的整体变化趋势相似，但相比等间距结构在波长为1/m(m为正整数)倍肋间距对应的波数处具有谱峰，不等间距结构在该处并无谱峰存在，表明不等间距圆柱壳抑制波长为1/m倍肋间距的结构波是产生安德森定域效应的根本原因；②在391 Hz，等间距加肋圆柱壳肋间振动主要为半波振动，虽然不等间距加肋圆柱壳有效抑制了该种结构波，但并未使得如图4所示的总振动出现明显衰减，其原因是该频率下等间距与不等间距结构均存在较大的长波振动，湮没了肋间振动的特征；③在544 Hz，不等间距加肋圆柱壳各轴向波振动功率均大于等间距加肋圆柱壳，其原因为等间距加肋圆柱壳振动在该频率处于止带，结构波传播衰减较大，同时虽然肋骨不等间距布置对结构波传播也具有较大衰减，但由于肋间距多样化，存在局部振动相比等间距结构较大的情况(见图6)，表现在波数谱上即为所有波数的振动功率整体提高。

(a) 391 Hz (b) 637 Hz (c) 862 Hz (d) 544 Hz图5 等间距与不等间距加肋圆柱壳在典型频率处的周向n=0阶法向速度振动功率波数谱Fig.5 The normal velocity vibration power wavenumber spectrum of periodic and aperiodic ribbed cylindrical shell in typical frequencies corresponding to n=0

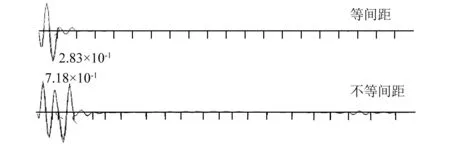
图6 等间距与不等间距加肋圆柱壳544 Hz时壳体振形Fig.6 Vibration shapes of periodic and aperiodic ribbed cylindrical shell in 544 Hz

4 不等间距加肋圆柱壳周向波数谱分析

选取上述的等间距与不等间距加肋圆柱壳结构，去除两端端盖后作为分析模型。

在模型左端施加垂直正弦点激励，若将此种激励在周向上进行空间域的分解，可当作多种周向阶数模式的环形径向激励的叠加，且各模式激励的幅值相当，有利于后续对壳体各周向阶振动的特性进行分析。同理，若圆柱壳在端部添加端盖，在垂向激励下，壳体响应则以周向n=1阶的振动模式为主，不利于各周向阶振动模式的比较分析，因此模型不加端盖。模型采用自由边界条件。

图7以分别代表圆柱壳周向低阶(n=1)与高阶(n=9)的振动为例，对等间距与不等间距加肋圆柱壳各周向阶法向速度振动功率频率特性进行对比分析。易见：①对任意周向阶振动，肋骨的不等间距布置均表现出较好的安德森定域效应，使得通带处振动有较大衰减；②肋骨不等间距布置形式同时也使得各周向阶振动在止带处有所增强；③结合轴向波数谱与振形(见图6)可知，局部结构尤其是激励源附近结构的振动增强是不等间距结构振动在止带增强的主要原因，因此若将肋骨不等间距布置结合局部结构补强措施可取得更好的结构减振降噪效果。

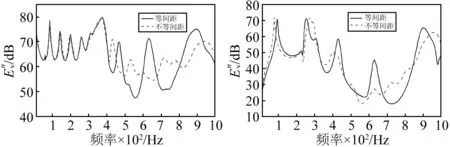
(a) n=1 (b) n=9图7 等间距与不等间距加肋圆柱壳的周向n=1、n=9阶法向速度振动功率Fig.7 The nomal velocity vibration power of periodic and aperiodic ribbed shell corresponding to n=1、n=9

5 肋骨布置的不规则程度对壳体结构声学特性影响研究

肋骨布置的不规则程度是描述肋骨不等间距布置形式的重要概念，令肋骨布置的不规则程度表示为

(11)

选取3个肋骨布置形式不同的不等间距加肋圆柱壳模型，其结构尺度均与前述圆柱壳相同，仅肋骨布置形式不同。3个模型肋骨布置的不规则程度分别为0.083、0.167、0.225，其肋骨布置形式见图8。

图8 不同肋骨布置形式示意图Fig.8 Different arrangement plan of ribs

在圆柱壳左端施加环形均匀的径向简谐激励，激励幅值为1 N(见图1)。计算时模型采用自由边界条件。

图9为不同肋骨布置不规则程度的圆柱壳均方法向速度级声学传递函数频率曲线。易见：①各不等间距加肋圆柱壳的振动特性相似，表明不等间距加肋圆柱壳结构声学性能优于等间距加肋圆柱壳的结论具有一般性，并非个例；②由于肋骨布置形式的不同，不同不等间距加肋圆柱壳的振动在止带的谱峰发生偏移；③在较宽频率范围内，肋骨布置的不规则程度越大，安德森定域效应越强，即其结构声学性能越优。

6 结 论

本文以不等间距加肋圆柱壳作为一般等间距结构布置圆柱壳的具体化对象，对其轴向与周向振动的一般性规律进行了研究，得出主要结论如下：

(1)肋骨布置形式对壳体振动的影响主要体现在结构波长小于肋间距的中高频，低频时影响不大；由此可以推论，由于舱壁之间布置间距较大，舱壁布置形式将对更低频段壳体振动产生影响。

(2)对圆柱壳任意周向阶振动，在通带频段，不等间距结构布置使得壳体振动均具有安德森定域效应，使得不等间加肋圆柱壳结构声学性能优于等间距加肋圆柱壳。产生安德森定域效应的原因为不等间距圆柱壳抑制波长为1/m倍肋间距的结构波。

(3)在等间距圆柱壳的止带，不等间距圆柱壳振动强于等间距加肋圆柱壳，主要体现为局部振动的增强，尤其是激励源附近结构振动的增强。因此，若将肋骨不等间距布置结合局部结构补强措施可取得更好的结构减振降噪效果。

(4)肋骨布置的不规则程度越大，则不等间距加肋圆柱壳的结构声学性能越优。

[ 1 ] 李正良，胡浩，于伟．正交加筋圆柱壳-球壳组合结构自由振动分析[J]．振动与冲击，2015，34(22)：129-137．

LI Zhengliang，HU Hao，YU Wei．Free vibration of joined and orthogonally stiffened cylindrical-spherical shells [J]．Journal of Vibration and Shock，2015，34(22)：129-137．

[ 2 ] MEAD D J，YAMAN Y．The response of infinite periodic beams to point harmonic forces: a flexural wave analysis[J]．Journal of Sound and Vibration，1991，144(3)：507-530．

[ 3 ] HODGES C H，WOODHOUSE J．Confinement of vibration by one-dimensional disorder I: theory of ensemble averaging [J]．Journal of Sound and Vibration，1989，130(2)：237-251．

[ 4 ] HODGES C H，WOODHOUSE J．Confinement of vibration by one-dimensional disorder II: a numerical experiment on different ensemble averages[J]．Journal of Sound and Vibration，1989，130(2)：253-268．

[ 5 ] PHOTIADIS D M，HOUSTON B H．Anderson localization of vibration on a framed cylindrical shell[J]．The Journal of Acoustical Society of America，1999，106(3)：1377-1391．

[ 6 ] MARCUS M H，HOUSTON B H，PHOTIADIS D M．Wave localization on a submerged cylindrical shell with rib aperiodicity[J]．The Journal of Acoustical Society of America，2001，109(3)：865-869．

[ 7 ] BANSAL A S, Flexural waves and deflection mode shapes of periodic and disordered beams[J]．The Journal of Acoustical Society of America，1982，72(2)：476-481．

[ 8 ] BANSAL A S, Free waves in periodically disordered systems: natural and bounding frequencies of unsymmetric systems and normal mode localization[J]．Journal of Sound and Vibration，1997，207(3)：365-382．

[ 9 ] HODGES C H，WOODHOUSE J．Vibration isolation from irregularity in a nearly periodic structure: theory and measurements[J]．The Journal of Acoustical Society of America，1983，74(3)：894-905．

[10] CASTANIER M P，PIERRE C．Individual and interactive mechanisms for localization and dissipation in a mono-coupled nearly-periodic structure[J]．Journal of Sound and Vibration，1993，168(3)：479-505．

[11] BOUZIT D, PIERRE C．An experimental investigation of vibration localization in disordered multi-span beams[J]．Journal of Sound and Vibration，1995，187(4)：649-669．

[12] BANSAL A S．Collective and localized modes of mono-coupled multi-span beams with large deterministic disorders[J]．The Journal of Acoustical Society of America，1997，102(6)：3806-3809．

[13] EATWELL G P．Free-wave propagation in an irregularly stiffened, fluid-loaded plate[J]．Journal of Sound and Vibration，1983，88(4)：507-522．

[14] PHOTIADIS D M．Anderson localization of one-dimensional wave propagation on a fluid-loaded plate[J]．The Journal of Acoustical Society of America，1992，91(2)：771-780．

[15] ANDERSON P W．Absence of diffusion in certain random lattices[J]．Physical Review,1958，109(5)：1492-1505．

[16] ISHII K．Localization of eigenstates and transport Phenomena in the one-dimensional disordered system[J]．Progress of Theoretical Physics Supplement，1973，53(53)：77-138．

[17] SOBNACK M B，CRIGHTON D G．Anderson localization effects in the transmission of energy down an irregularly ribbed fluid-loaded structure[J]．The Royal Society，1994，444：185-200．

[18] COOPER A J，CRIGHTON D G．Response of irregularly ribbed elastic structures, under fluid loading, to localized excitation[J]．The Royal Society，1999，455：1083-1105．

[19] ANDERSON P W，THOULESS D J，ABRAHAMS E，et al．A new method for a scaling theory of localization[J]．Physical Review B，1980，22(22)：3519-3526．

[20] HODGES C H．A simple interpretation of the absence of quantum diffusion for one and two dimensional disorder[J]．Journal of Physics C: Solid State Physics,1981，14(10)：247-253．

[21] 谭路，纪刚，张纬康，等．采用波数域方法分析细长柱壳的振动与声辐射特性[J]．海军工程大学学报，2013，25(3)：66-71．

TAN Lu，JI Gang，ZHANG Weikang，et al．Slender cylindrical vibration and radiation by use of wave-number domain approach[J]．Journal of Naval University of Engineering，2013，25(3)：66-71．

[22] HODGES C H．Confinement of vibration by structural irregularity[J]．Journal of Sound and Vibration，1982，82(3)：411-424．

[23] MEAD D J．Wave propagation in continuous periodic structures: research contributions from Southampton, 1964-1995[J]．Journal of Sound and Vibration，1996，190(3)：495-524．