酒杯型输电铁塔曲臂风荷载风洞试验研究
2018-01-23杨风利牛华伟杨靖波张宏杰
杨风利, 牛华伟, 杨靖波, 张宏杰
(1.中国电力科学研究院,北京 100192; 2.湖南大学 风工程试验研究中心,长沙 410082)
酒杯塔是单回输电线路的最常用塔型之一,在1 000 kV特高压输电工程中也得到广泛应用。而酒杯塔塔头由水平横担、上曲臂和下曲臂构成,其结构型式与单回路干字型塔、双回路伞型塔和鼓型塔塔头有较大差别。目前国内外设计规范[1-6]中均未针对酒杯塔塔头结构型式特点提出相应的风荷载计算方法,其体型系数和角度风荷载计算取值与常规输电铁塔相同。

图1 风压分段类型说明Fig.1 Illustration of the wind pressure segment
目前我国常用的输电铁塔结构设计软件有道亨、TTA等[7],其风压分段型式如图1所示。由于设计习惯差异且DL/T 5154—2012《架空输电线路杆塔结构设计技术规定》(以下简称“中国规范”)中未对曲臂风压分段归类做出明确规定,不同设计人员计算曲臂风荷载时所选分段类型并不一致,存在分别按照图1所示的“横担”或“塔身”型式进行计算的情况,造成酒杯塔曲臂风荷载存在差异。风荷载是输电铁塔的主要控制荷载,图2所示的1 000 kV特高压酒杯塔塔高73 m,上、下曲臂高度分别达到12.24 m和21.79 m。随着特高压工程建设规模的逐渐增大,加之特高压输电线路的重要性和可靠性相对一般线路有更高的要求,因此需要通过风洞试验或理论分析,研究酒杯塔塔头横担和曲臂的平均阻力系数、背风面风荷载降低系数和角度风分配系数等风荷载计算参数,为更准确的计算酒杯塔塔头风荷载提供参考和依据。

图2 1 000 kV特高压酒杯塔Fig.2 Cup-type tower of 1 000 kV UHV transmission lines
国内外学者已采用高频测力风洞试验开展了大量输电铁塔平均阻力系数(体型系数)方面的研究工作。Bayar[8]通过刚体模型高频天平测力风洞试验,识别了不同风向角下正方形断面格构式塔架的平均阻力系数,其在45°风向下的平均阻力系数最大。邹良浩等[9]利用高频测力天平风洞试验分别得到了猫头型输电铁塔的整体基底弯矩、基底剪力时程,提出了格构式塔架的风载体型系数取值方法,进而计算出塔架在不同工况下的风载体型系数。张庆华等[10]通过高频底座天平测力风洞试验,得到了典型500 kV酒杯型和猫头型输电塔塔头结构风力系数的平均值和根方差值,给出了极值风力下塔头结构顺风向、横风向基底剪力和基底扭矩的功率谱。邓洪洲等[11]对1 000 kV淮南—上海特高压输电线路钢管塔的塔身-横担连体模型进行了高频天平测力风洞试验,得到了模型的平均风荷载和平均阻力系数,认为风向与横担轴向夹角为15°左右时,连体模型的风荷载最大。Mara等[12]采用塔身与横担组合模型,通过风洞试验研究了角度风作用下的横担设计荷载;认为横担的空气动力特性比塔身复杂,讨论了风洞试验值与ASCE规范计算值的差异。已有成果可为开展酒杯型输电铁塔塔头风荷载风洞试验及理论分析研究提供重要的参考和借鉴,但上述文献尚未针对酒杯塔曲臂的体型系数、背风面风荷载降低系数和角度风荷载分别进行系统研究并给出相关结论。
本文完成了15 m/s和20 m/s来流风速下酒杯型输电铁塔曲臂模型的风洞试验,得到了不同风向角下的风轴和体轴平均阻力系数,获得了曲臂模型迎风面、背风面体型系数和背风面风荷载降低系数η,分析了酒杯型输电铁塔曲臂角度风荷载系数和有效投影面积,将试验确定的酒杯型输电铁塔曲臂角度风荷载计算参数与国内外规范计算值进行了对比分析,提出了酒杯型输电铁塔曲臂角度风荷载的设计取值建议。
1 模型选取及设计风荷载差异
为尽量增大风洞试验模型的缩尺比例,以220 kV输电线路2B1-ZB1型酒杯塔作为研究对象,该塔塔高39 m,设计风速取10 m高、10 min平均风速23.5 m/s,铁塔风荷载调整系数βz=1.34。考虑节点板、螺栓等影响,设计时杆件投影面积的增大系数取1.60。在输电铁塔设计软件TTA中,可分别按照图1中的“横担”或“塔身”两种风压分段类型,计算2B1-ZB1型酒杯塔上曲臂风荷载,正面和侧面风荷载计算参数及整体风荷载Ws计算结果对比见表1。根据中国规范表3.1.3关于铁塔塔身角度风荷载计算规定,0°、45°、60°和90°风作用下,按“横担”和“塔身”两种类型计算得到上曲臂的节点风荷载见表2。表1和表2中参数b/a、φ和η分别表示曲臂宽高比、挡风系数和背风面风荷载降低系数。

表1 上曲臂风荷载对比

表2 上曲臂节点角度风荷载
结合中国规范表3.1.3和表2可以看出,按“横担”和“塔身”两种模型计算得到的0°风横线向风荷载FX和90°风顺线向风荷载FY相同(均为0);由于按“横担”模型计算角度风荷载时,侧面风荷载仅计入迎风面风荷载,不考虑背风面风荷载影响(即背风面风荷载降低系数η=0),按“塔身”模型计算得到的45°、60°横线向风荷载FX及顺线向风荷载FY比按“横担”模型的计算值高约14.4%和20.0%,90°横线向风荷载FX高约21.2%,说明模型选择对酒杯型输电铁塔曲臂设计风荷载的影响不可忽略。
2 风洞试验及数据分析
2.1 试验概况
风洞试验在湖南大学风工程试验研究中心HD-2风洞完成,测试时风场为均匀流场,湍流强度不超过0.2%,风速参考高度为0.5 m。2B1-ZB1型酒杯塔塔头全部由角钢构件组成,模型几何缩尺比例为1∶10,尺寸如图3所示。上、下曲臂模型的正面投影面积Aml分别为0.011 4 m2和0.013 1 m2,挡风系数φ分别为0.392和0.366;侧面投影面积Amt分别为0.015 0 m2和0.018 5 m2,挡风系数φ分别为0.313和0.229。

图3 模型几何尺寸(单位:mm)Fig.3 Geometrical dimensions of the model(unit:mm)
来流风向角规定如图4所示,风向角θ为来流方向与输电线路顺线向的夹角,顺线向即与曲臂正面垂直的方向。定义0°风时Y轴负方向指向来流,即此时模型受到的阻力为正值,X轴向右。曲臂模型无量纲的力系数可按照式(1)求出
Ci=Fi/(0.5ρV2S)
(1)
式中:i=X、Y、Z,为体轴坐标系对应的三个主方向;Fi和Ci分别为i向气动力及其对应的气动力系数;V为来流平均风速,为验证来流风速与角钢横担模型阻力系数的无关性,取15 m/s和20 m/s;ρ为空气密度,取1.225 kg·m-3;S为参考面积,取0°风向角时曲臂正面的迎风面投影面积。
将式(1)计算得到的体轴阻力系数CXθ、CYθ沿风轴坐标系方向投影,即可得到曲臂模型的风轴阻力系数CDθ和升力系数CDθ,CDθ和CLθ的计算式为
《数据库维护与编程》是计算机科学与技术、软件工程等计算机类专业的核心课程之一,实践性和操作性都很强。数据库技术是管理信息系统、办公自动化系统、决策支持系统等各类信息系统的核心部分,是进行科学研究和决策管理的重要技术手段[1]。所以,熟练掌握数据库维护与编程技术,对计算机类专业的学生尤为重要。
CDθ=(CXθcosθ+CYθsinθ)CLθ=(CYθcosθ-CXθsinθ)
(2)
根据式(2),曲臂风荷载合力力系数CRθ的计算式为
(3)

图4 曲臂风向说明Fig.4 Demonstration of the wind incidence angle of the crank arm
2.2 平均阻力系数
曲臂测力模型的试验照片如图5所示,其中塔身连接段用于消除底部不稳定风场对曲臂测力准确性的干扰。将图5(a)所示的上曲臂、下曲臂和塔身连接段整体模型一起进行测力试验,而后单独进行图5(b)所示的下曲臂和塔身连接段模型测力试验,两段模型测力值相减得到上曲臂模型的力;将图5(b)所示的下曲臂模型与塔身连接段一起进行测力试验,而后单独进行图5(c)所示的塔身连接段模型测力试验,两段模型测力值相减得到下曲臂模型的力。
15 m/s和20 m/s来流风速、11种风向角下(0°、10°、20°、30°、40°、45°、50°、60°、70°、80°、90°),上曲臂和下曲臂模型的体轴平均阻力系数CXθ、CYθ及风轴平均阻力系数CDθ的试验曲线分别见图6(a)和图6(b)。由图6可以看出,两种风速下的风轴平均阻力系数CDθ变化较小,上曲臂相差1.5%~6.3%,下曲臂相差-0.1%~2.0%,说明来流风速对角钢曲臂模型气动力系数的影响较小。曲臂体轴平均阻力系数CXθ、CYθ分别在风向角θ为70°和20°时达到最大值,即横线向风荷载FX和顺线向风荷载FY分别达到最大值;风向角θ为60°时,曲臂风轴平均阻力系数CDθ最大,曲臂整体风荷载达到最大值。

图5 曲臂模型测力风洞试验模型Fig.5 Photos of the crank arms for wind force tests

图6 曲臂风轴、体轴平均阻力系数曲线Fig.6 Drag coefficients of the crank arms in body-fitted axis and wind directional axis
来流方向与曲臂正面垂直时(θ=0°),风洞试验得到的曲臂平均阻力系数和国内外规范规定的平均阻力系数值见表3。ASCE和IEC规范中未考虑宽高比b/a变化对平均阻力系数的影响,其他规范宽高比取曲臂侧面主材中心线距离b与正面主材中心线距离a之比(见图4)。由表3可以看出,ASCE、IEC和中国规范曲臂平均阻力系数低于风洞试验值,JEC和英国规范计算值高于风洞试验值,英国规范的平均阻力系数计算值与试验值最为接近;中国规范计算值最小,上曲臂和下曲臂平均阻力系数计算值分别比试验值低9.7%和18.3%。
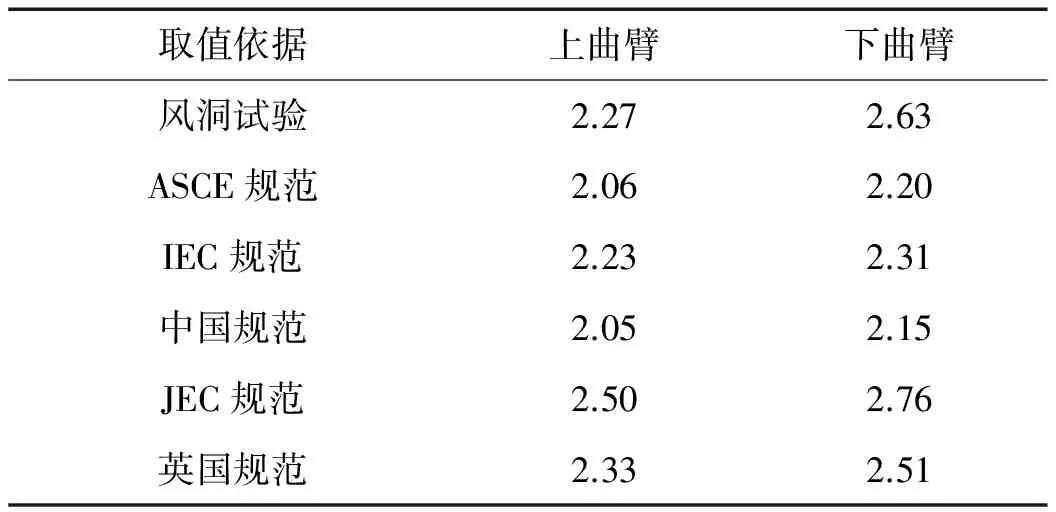
表3 曲臂平均阻力系数
2.3 背风面风荷载降低系数η
表征迎风面屏蔽效应的设计参数为背风面风荷载降低系数η。上曲臂模型屏蔽效应测试照片如图7所示,分别把曲臂迎风面或背风面单独安装在测力天平上,另一个面安装在滑动导轨上移动以考虑其遮挡效应。试验时将曲臂的某个面(迎风面或背风面)安装在测力天平上,而另一个面则不与测力天平连接,便能测出每个面的体型系数,将背风面体型系数CDb与迎风面体型系数CDf相比可以得到背风面风荷载降低系数η。由2.1节可知,风速变化对角钢曲臂平均阻力系数影响较小,本节仅对15 m/s风速作用下的上曲臂背风面降低系数η进行分析,研究风向角θ及宽高比b/a对屏蔽效应的影响。

图7 屏蔽效应测试照片Fig.7 Photos of the shielding effect test
上曲臂模型3种宽高比b/a、10种风向角θ时的迎风面体型系数CDf、背风面体型系数CDb、背风面风荷载降低系数η见表4~表6。背风面风荷载降低系数η随风向角θ的变化逐渐改变,θ=0°时迎风面对背风面风荷载的遮挡效应最为明显。下曲臂不同风向角时的背风面风荷载降低系数不再详述。由于现行规范一般采用风向与迎风面垂直的单片桁架体型系数并考虑背风面风荷载降低影响,计算得到桁架整体体型系数,因此本次分析重点关注试验中风向角θ=0°时的背风面风荷载降低系数。由表4~表6可见,随宽高比b/a的增大,θ=0°时上曲臂背风面风荷载降低系数η逐渐增大,即背风面的遮挡效应逐渐降低。

图8 背风面风荷载降低系数η拟合曲线Fig.8 The fitting curve of shielding factor η
背风面风荷载降低系数η随风向角θ的变化曲线如图8所示。由图8可见,η随风向角θ呈非线性变化趋势,θ=60°或70°时,η达到最大值。
由风洞试验结果分析得到上曲臂的背风面风荷载降低系数及与中国规范和英国规范计算值的对比情况见表7。由表7可以看出,对于角钢曲臂,当宽高比b/a分别为1.67、2.0和3.0时,中国规范和英国规范的背风面风荷载降低系数η计算值偏小,中国规范计算值比试验值低6.5%~16.8%,英国规范计算值比试验值低32.1%~38.4%。
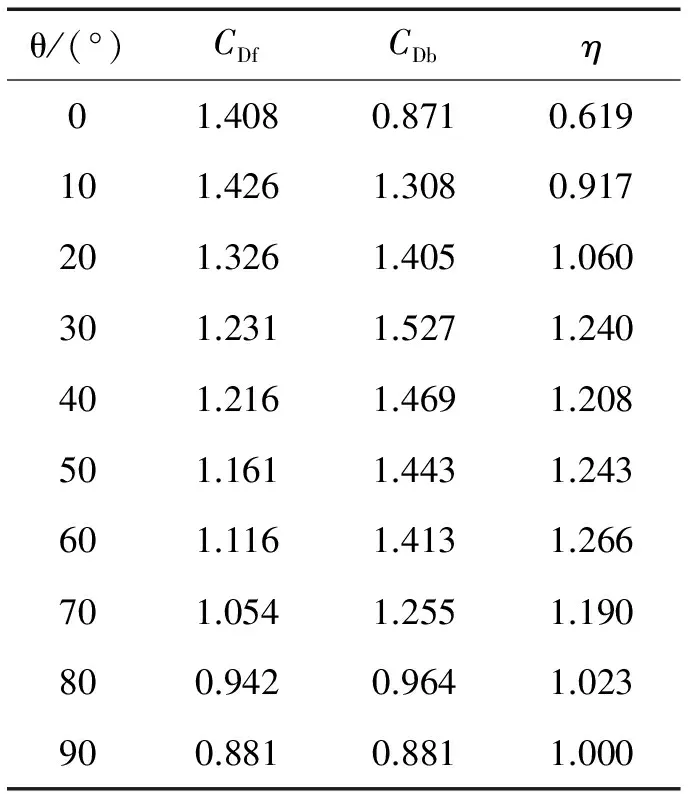
表4 上曲臂模型风洞试验值(b/a=1.67)

表5 上曲臂模型风洞试验值(b/a=2.0)

表6 上曲臂模型风洞试验值(b/a=3.0)

表7 背风面风荷载降低系数η对比
2.4 角度风荷载系数Kθ
ASCE(1991)、IEC等规范关于角度风作用下曲臂风荷载的计算公式为
(4)
式中:FD为曲臂沿风轴的阻力,不考虑沿风轴升力FL的影响;CD为风向与曲臂正面垂直时(θ=0°)时,曲臂的平均阻力系数;Ac为曲臂迎风面投影面积,即0°风时曲臂正面构件的迎风面投影面积,这一规定与风洞试验中参考面积S的定义相同;角度风荷载系数Kθ=CDθ/CD。
由JEC规范和Yang等[13]的研究成果可知,沿风轴的升力对两个体轴的风荷载均会产生影响,进而影响塔身或横担的角度风荷载系数取值。考虑升力影响的曲臂风荷载合力的计算公式为
(5)
式中:CR是风向与曲臂正面垂直时(θ=0°),曲臂的风荷载合力系数,CR≈CD;角度风荷载系数Kθ=CRθ/CR。
来流风速15 m/s、风向角θ在0°~90°内变化时,上、下曲臂风荷载合力系数CRθ与风轴平均阻力系数CDθ的曲线对比如图9所示。可以看出,曲臂合力CRθ与风轴阻力CDθ基本一致,最大相对差值小于1%,即升力对曲臂合力的贡献可以忽略。下面将采用Kθ=CDθ/CD计算曲臂的角度风系数。

图9 曲臂合力系数与平均阻力系数曲线Fig.9 Resultant force coefficients and drag coefficients of the crank arms
15 m/s来流风速作用上曲臂和下曲臂的Kθ计算结果见表8,θ=60°时的Kθ值最大,即此时曲臂整体沿风轴的平均阻力系数最大,曲臂承受的风荷载达到最大值。上曲臂和下曲臂Kθ试验曲线与ASCE规范曲线的对比如图10所示。可以看出,θ=45°时,ASCE规范的Kθ计算值最大;当10°≤θ≤90°时,Kθ试验值均高于ASCE规范计算值。

表8 曲臂角度风荷载系数试验值
2.5 有效投影面积
国内外规范在计算输电铁塔塔身或横担角度风荷载时,有些采用正面投影面积作为基准计算,有些则采用正、侧面风荷载进行组合计算。由2.2节可知,中国规范的曲臂平均阻力系数与国外规范也存在较大差异。为便于比较各国规范曲臂角度风风荷载的差异,引入“有效投影面积(Effective Projected Areas, EPA)”CDAp反映角度风作用下曲臂整体合力的变化趋势,国内外规范有效投影面积(CDAp)θ及其在横线向和顺线向分量(CDAp)θt、(CDAp)θt的计算方法见表9。

表9 有效投影面积

图10 角度风荷载系数对比Fig.10 Comparison of the skewed wind load factors
由风洞试验和国内外规范计算得到的曲臂有效投影面积见图11。由图11(a)可以看出,风向角为0°≤θ≤40°时,规范计算的曲臂整体有效投影面积低于风洞试验值,风洞试验曲线与ASCE(1991)和按中国规范“塔身”计算曲线的趋势基本一致,整体有效投影面积在θ=60°达到最大值。对于输电铁塔设计所关注的四个控制风向角0°、45°、60°、90°,风洞试验值比ASCE(1991)和按中国规范“塔身”模型计算值低约0%、3.9%、7.2%和31.6%,说明按中国规范“塔身”模型计算曲臂风荷载满足安全要求,但θ=90°时曲臂风整体风荷载取值偏于保守。θ=45°、60°和90°时,按中国规范“横担”模型计算的曲臂有效投影面积远低于风洞试验值,计算值与试验值分别相差约19.9%、26.8%和19.6%,将低估曲臂风荷载并使结构抗风设计存在安全隐患。由图11(b)可以看出,风向角为0°≤θ≤70°时,曲臂横线向有效投影面积风洞试验曲线与ASCE(1991)、ASCE(2010)和按中国规范“塔身”模型所得计算曲线基本一致,曲臂横线向有效投影面积在达到最大值;θ为80°和90°时,ASCE(1991)和按中国规范“塔身”模型计算值比风洞试验值分别高出14.7%和31.7%。由图11(c)可以看出,风向角为30°≤θ≤70°时,曲臂顺线向有效投影面积的风洞试验曲线与规范计算曲线基本一致;0°<θ<30°时,规范计算值小于风洞试验值,即现行规范可能低估曲臂顺线向的风荷载。
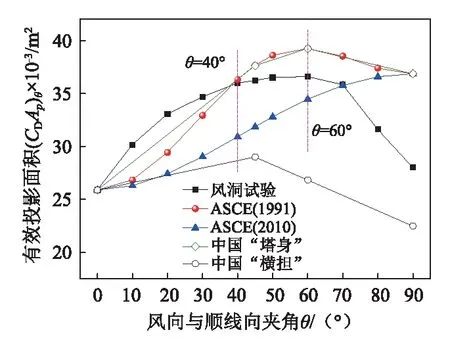
(a)整体有效投影面积
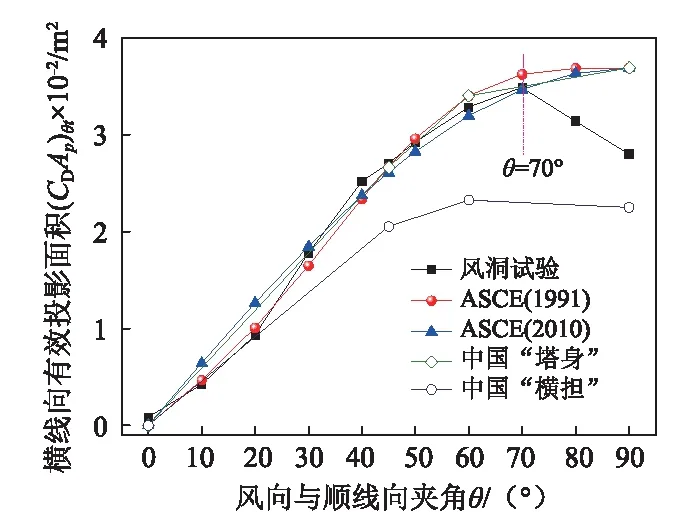
(b)横线向有效投影面积

(c)顺线向有效投影面积
3 结 论
本文讨论了目前设计时采用“塔身”模型和“横担”模型对计算曲臂风荷载的影响,通过风洞试验研究了酒杯型输电铁塔曲臂平均阻力系数、背风面风荷载降低系数和角度风计算方法,提出了酒杯型输电铁塔曲臂风荷载的设计建议。主要结论如下:
(1)15 m/s和20 m/s两种来流风速下的角钢曲臂模型阻力系数变化较小,来流风速对角钢曲臂模型阻力系数的影响可以忽略。
(2)模型选择对酒杯型输电铁塔曲臂设计风荷载的影响不可忽略。以2B-ZB1塔为例,按“塔身”模型计算得到的45°、60°横线向风荷载FX及顺线向风荷载FY比按“横担”模型的计算值高约14.4%和20.0%,90°横线向风荷载FX高约21.2%。
(3)ASCE、IEC和中国规范曲臂平均阻力系数低于风洞试验值,JEC和英国规范计算值高于风洞试验值,英国规范的平均阻力系数计算值与试验值最为接近;中国规范计算值最小,上曲臂和下曲臂计算值分别比试验值低9.7%和18.3%。
(4)酒杯型输电铁塔曲臂背风面风荷载降低系数η随风向角θ呈非线性变化趋势,θ为60°或70°时η达到最大值。背风面风荷载降低系数η按照中国规范取值偏低,宽高比b/a分别为1.67、2.0和3.0时,风洞试验值比中国规范计算值高6.5%~16.8%。
(5)按中国规范“塔身”模型计算曲臂风荷载满足安全要求,但风向角θ=90°时曲臂风整体风荷载取值偏于保守;θ为45°、60°和90°时,按中国规范“横担”模型计算的曲臂风荷载远低于风洞试验值,将低估曲臂风荷载并使结构抗风设计存在安全隐患。
[ 1 ] 架空输电线路杆塔结构设计技术规定:DL/T 5154—2012 [S].北京:中国计划出版社, 2012.
[ 2 ] American society of civil engineers.ASCE manuals and reports on engineering practice No.74[S].Reston:American Society of Civil Engineers,1991.
[ 3 ] American society of civil engineers.ASCE manuals and reports on engineering practice No.74[S].Reston:American Society of Civil Engineers, 2010.
[ 4 ] International electrotechnical commission. Design criteria of overhead transmission lines:IEC 60826 [S].Geneva:International electrotechnical commission, 2003.
[ 5 ] Japanese electrotechnical committee. Design standards on structures for transmissions:JEC-127—1979 [S]. Tokyo: JEC, 1979.
[ 6 ] British standards institution. Lattice tower and masts-Part1:Code of practice for loading :BS-8100:1986 [S].London:British Standards Institution,2005.
[ 7 ] 吕付玉,刘宏滨.道亨铁塔满应力分析软件与自立式铁塔内力分析软件的对比分析[J]. 广东电力,2011,24(6): 31-34.
LÜ Fuyu,LIU Hongbin.Comparative analysis of daoheng MYL software and TTA software[J].Guangdong Electric Power,2011,24(6): 31-34.
[ 8 ] BAYAR D C.Drag coefficients of latticed towers [J]. Journal of Structural Engineering,1986,112(2): 417-430.
[ 9 ] 邹良浩,梁枢果,邹垚,等.格构式塔架风载体型系数的风洞试验研究[J]. 特种结构,2008,25(5): 41-43.
ZOU Lianghao,LIANG Shuguo,ZOU Yao,et al.Wind tunnel test on wind load shape coefficients of lattice towers[J].Special Structures,2008,25(5): 41-43.
[10] 张庆华,顾明,黄鹏.典型输电塔塔头风力特性试验研究[J]. 振动工程学报,2008,21(5): 452-457.
ZHANG Qinghua,GU Ming,HUANG Peng.Experiment on wind force on typical superstructures of latticed transmission tower[J].Journal of Vibration Engineering,2008,21(5): 452-457.
[11] 邓洪洲,张建明,帅群,等.输电钢管塔体型系数风洞试验研究[J]. 电网技术,2010,34(9): 190-194.
DENG Hongzhou,ZHANG Jianming,SHUAI Qun,et al.Wind-tunnel investigation on pressure coefficient of steel tubular transmission tower[J].Power System Technology,2010,34(9): 190-194.
[12] MARA T G, HO T C E.Design loads for transmission towers under skewed wind loading[C]∥ Structures Congress 2011. Las Vegas: American Society of Civil Engineers,2001: 1246-1257.
[13] YANG Fengli, YANG Jingbo, NIU Huawei,et al.Design wind loads for tubular-angle steel cross-arms of transmission towers under skewed wind loading[J]. Journal of Wind Engineering and Industrial Aerodynamics,2015,140:10-18.
