系统参数对超空泡航行体非线性动力学特性的影响
2018-01-23吕一品熊天红易文俊
吕一品, 熊天红, 易文俊, 管 军
(南京理工大学 瞬态物理国家重点实验室,南京 210094)
当航行体在水中运动时,若水中某点的压力降低到临界压力以下,水将发生汽化,先是微观的,进而发展成宏观的小气泡,然后在水中或水与航行体的交界面上,汇合形成较大的蒸汽与气体空腔,称为空泡,若整个航行体表面以及尾端附近的水中都出现空泡,犹如一个大汽袋,将整个航行体装于其中,这种空泡称为超空泡[1-2]。形成超空泡之后,水的阻力就变为由水蒸气构成的空泡的阻力,大大地提高了运动速度,实现了航行体在水中飞行。但由于复杂的水动力特性具有时滞性、不确定性和时变性等问题,超空泡航行体的运动极容易受到周围干扰因素的影响,系统参数如空化数、空化器直径等能够改变超空泡的尺寸,造成航行体尾部与空泡之间的碰撞,产生非线性滑行力,进而造成航行体的振动[3-6],使航行体的运动具有强烈的非线性动力学特性。
在工程应用中,非线性动力学特性是超空泡航行体稳定控制的重要理论依据,Lin等[7]提出了超空泡航行体系统随着空化数的变化具有复杂的非线性动力学行为;白涛等[8]分叉分析了当尾翼偏转角变化时航行体的运动稳定性;熊天红等[9]探讨了超空泡系统随空化器偏转角的变化而产生的非线性物理现象。现有的研究多停留在单一参数的变化对超空泡航行体非线性动力学特性的影响。本文将从非线性的角度对超空泡航行体系统进行分析,运用Lyapunov稳定性理论确定超空泡系统动力学行为与参数的对应关系,探讨系统随多个参数变化产生的非线性物理现象,揭示其稳定运动的参数条件以及运动特性,为超空泡航行体控制器的设计提供理论研究基础。
1 水下超空泡航行体的动力学描述
1.1 超空泡航行体的外形
超空泡航行体的外形结构如图1所示,主要构成有:头部直径为D的圆盘空化器,前端圆锥段和后端半径为R的圆柱段,以及采用十字形布局的鳍舵,圆锥段长度是圆柱段的一半, 4个尾翼对称地布置在航行体的尾端。

图1 超空泡航行体示意图Fig.1 Schematic diagram of a supercavitating vehicle
流场的外部条件和水下航行体几何形状等都会使空泡出现不同的状态,通常用空化数σ来表征相似的空泡状态,定义为σ=2(p∞-pc)/ΡV2,其中,P∞为无穷远处的压力,Pc为空泡内部的压力,ρ为水的密度,V为航行体的合速度。
当航行体高速运动时,与水接触的只有空化器和尾翼,空泡尺寸会随着空化数的减小而增大,可以通过改变空化数来改变流场的空化状态;合理调节尾翼偏转角度不仅能够控制航行体在超空泡内的姿态,还能有效地抑制非线性滑行力的出现,提高航行体的稳定性;另外,超空泡形态的优良率与空化器直径密切相关[10]。故通常将空化数、空化器直径和尾翼偏转角作为可变参数来分析其对超空泡航行体动力学特性的影响。
1.2 超空泡航行体动力学模型
图2所示,超空泡航行体动力学建模的体坐标系原点位于航行体头部空化器顶端面的圆心,X轴的方向与航行体的中心轴线重合指向前,Y轴的方向垂直于中心轴线指向下,把地面系当作惯性系, 本文研究航行体在纵平面内的运动。建模采用航行体所处的深度z、垂直速度w、俯仰角θ、俯仰角速度q作为状态变量来描述其动力学,垂直速度w的方向与Y轴方向一致,V为纵平面内航行体的合速度,X轴方向的速度为Vx。另外,系统具有两个控制输入,分别为尾翼偏转角δe和空化器偏转角δc。
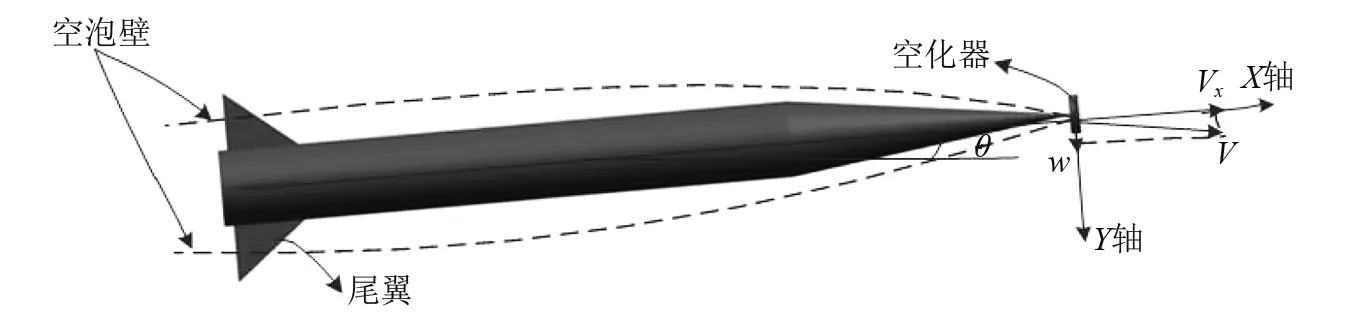
图2 超空泡航行体纵向建模示意图Fig.2 The longitudinal model of a supercavitating vehicle
根据航行体各部分所受的流体动力[11],结合动量和动量距定理可以推出上述变量有如下关系[12]
(1)
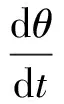
(2)
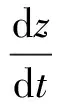
(3)
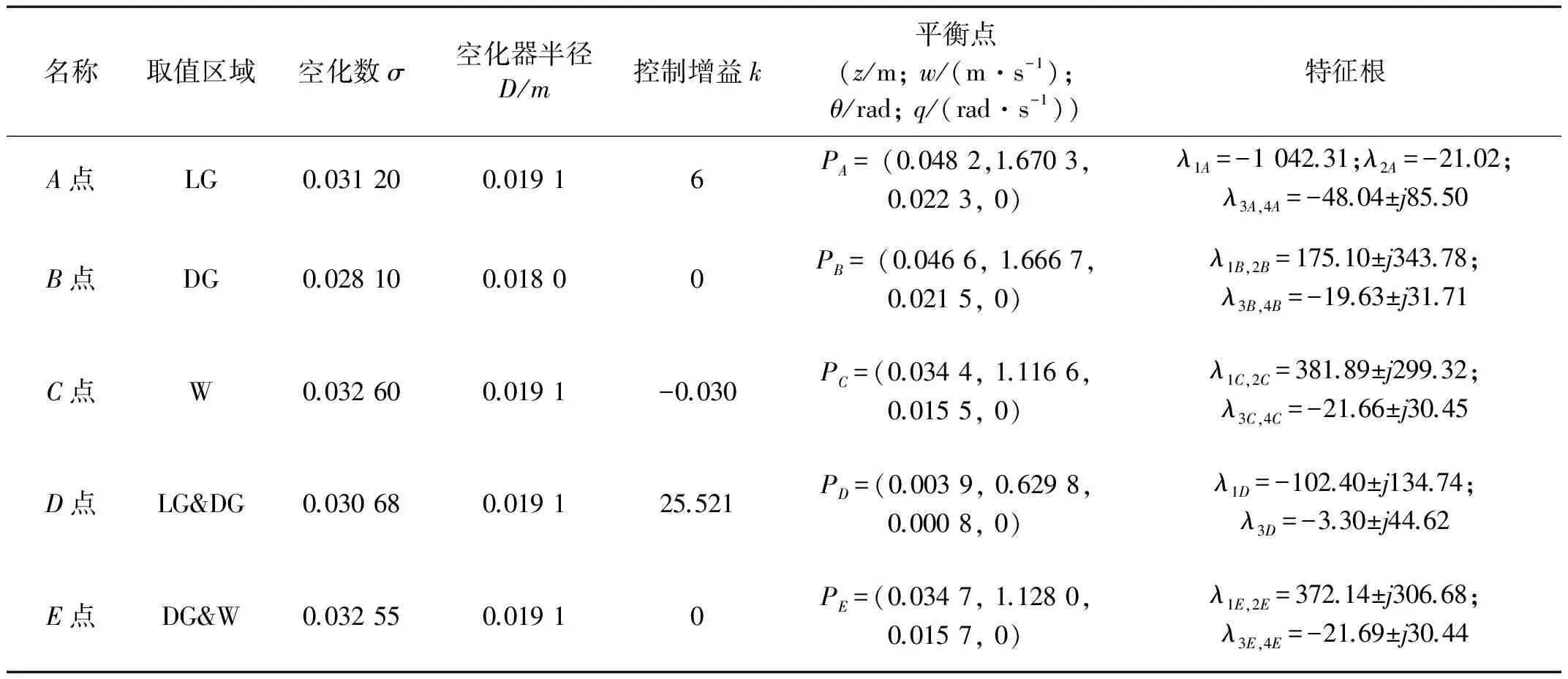
超空泡航行体模型参数值如表1所示。
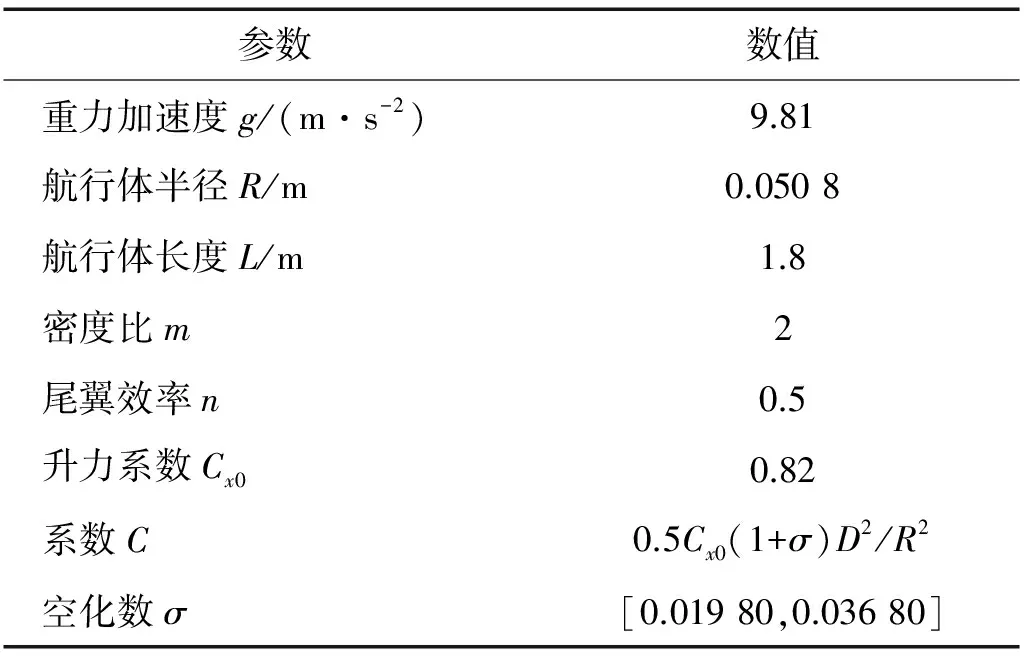
表1 超空泡航行体的参数值
当空化器直径D较小时,不能形成空泡或者形成部分空泡,而过大的空化器直径在降低航行体摩擦阻力的同时大幅度增加了压差阻力,导致减阻效果不明显,即D过大过小都不利于超空泡航行体的航行。因此本文选取空化器直径D的研究范围为[0.010 0,0.030 0] m。
Dzielski 等提出了经典控制律δe=0、δc=15z-30θ-0.3q,但由于尾翼偏转角为零,往往会使航行体缺乏尾翼提供的支持力,当空化器提供的升力不能平衡航行体的重力时,将导致航行体在重力的作用下浸入空泡而失稳。因此,本文令控制律为δe1=kq、δc1=15z-30θ-0.3q,k为航行体俯仰角速度q的反馈控制增益,整理式(1)~式(3)式可得到以空化器直径D、空化数σ、尾翼偏转角反馈控制增益k为可变参数的动力学方程式
(4)
式中:C=158.914 7(1+σ)D2;a22=-4.207 9CV+0.425 0;a24=-6.154 0CV+14.710 1V;a42=1.515 4CV;a44=-1.304 6CV;b21=0.616 7CV2;b22= -2.805 4CV2;b41=-0.724 9CV2;b42=2.240 6CV2;d2=-1.226 6;d4=1.449 2。Fplaning为航行体尾部与空泡碰撞产生的非线性滑行力,该力的出现往往会导致航行体产生振动与冲击。滑行力表达式
(5)
式中:R′=Rc-R,Rc为空泡半径,R为航行体半径;h为航行体尾部探出空泡的深度,称作浸没深度;α为航行体中心线与空泡中心线之间的几何角为浸没角,其表达式为
(6)
(7)
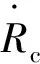
2 超空泡航行体的动力学特性
2.1 超空泡航行体的动力学地图
为完整地展现超空泡航行体的动力学行为与参数的依赖关系,本文基于动力学模型(4),随机地选取初始条件,依照Lyapunov稳定性理论[13]将模型的稳定解、周期解、混沌解用不同的颜色在图3中表示出来,绘制出超空泡航行体的动力学地图。图中浅灰色区域LG表示航行体稳定运动;深灰色区域DG表示航行体周期振荡;白色区域W表示航行体会出现剧烈的振动与冲击;黑色区域D表示系统发散。图3 (a)为空化器直径D=0.019 1 m时,分岔参数σ和k所定义的动力学地图;图3(b)为尾翼偏转角反馈控制增益k=0时,分岔参数σ和D所定义的动力学地图。
根据图3(a)能够确定航行体稳定运动的σ和k的取值范围。当σ确定时,只要在对应LG区域内调节k的取值,就能够有效实现超空泡航行体的稳定航行,对航行体的稳定性控制具有指导意义。前文提到航行体空化器直径D过小或者过大都不利于超空泡减阻效果,结合图3(b)可以选择合适的D,既能形成将航行体包裹住的完整空泡又不至于形成的空泡厚度过大而增加航行阻力,对超空泡航行体稳定高速地运动具有实际指导意义。
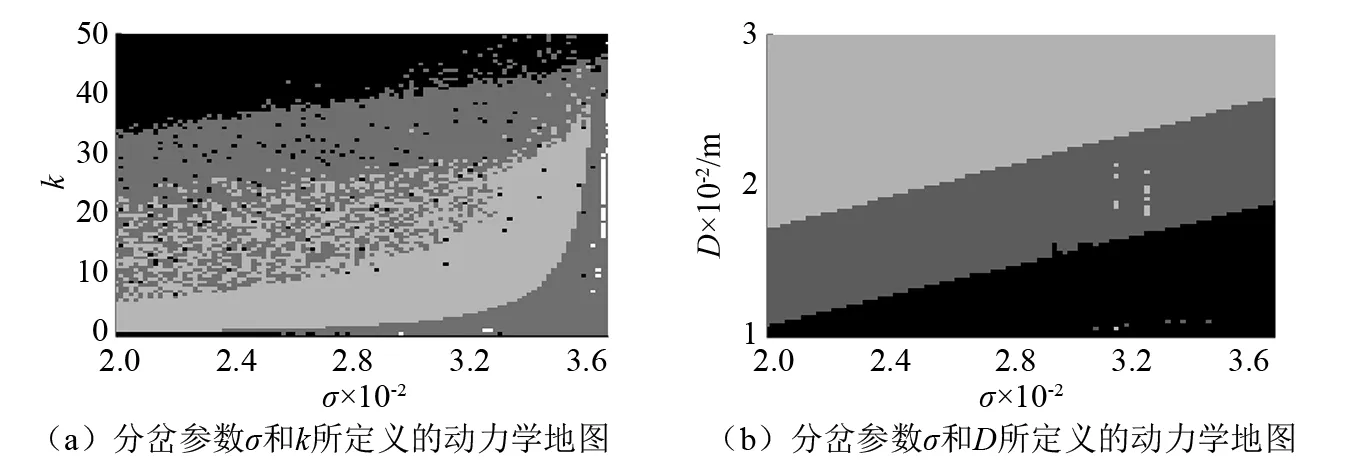
图3 动力学地图 Fig.3 Regions of different dynamical behaviors
分别在图3中的LG区域、DG区域和W区域中各随机地选取一点,图4为三种状态的相轨迹图。LG区域中选取的系统参数为σ1=0.031 20,D1=0.019 1 m,k1=6,如图4(a)所示,垂直速度w和俯仰角θ在反馈控制律的作用下被吸引到稳定平衡点上,航行体在该参数的作用下稳定航行。
DG区域中选取的参数为:σ2=0.028 10,D2=0.018 0 m,k2=0,相轨迹如图4(b)所示,系统映射形成了闭合极限环,极限环与临界切换分界线w=wth相交,其中wth=(Rc-R)V/L,Rc为空泡半径,垂直速度w时而大于wth,时而小于wth,航行体尾部不时地摆动与空泡碰触,引起滑行力周期性的变化,尾部时而穿过空泡插入水中,产生滑行力,时而被空泡包裹,无滑行力,航行体周期振荡。
W区域中选取的参数为:σ3=0.032 60,D3=0.019 1 m,k3=-0.030,相轨如图4(c)所示,混沌吸引子的出现表明航行体的运动具有复杂的非线性动力学行为。
图3(a)相对完整地反应了航行体随参数σ、k变化时所处的不同状态,深灰色周期振荡是主要的运动状态,周期振荡对应的极限环也是主要的动力学行为。当k∈[1.041,5.122]时,航行体稳定运动的空化数σ取值范围较大;当k∈[5.121,27.553]时,浅灰色稳定点星罗棋布地洒在深灰色周期区域中,σ的微小变化总是会引起运动状态在稳定与周期之间转变;研究该区域还发现,在某些参数处,通过仿真计算,随机设置初始值,航行体表现出不同的动力学行为。
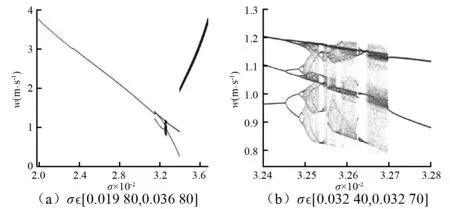
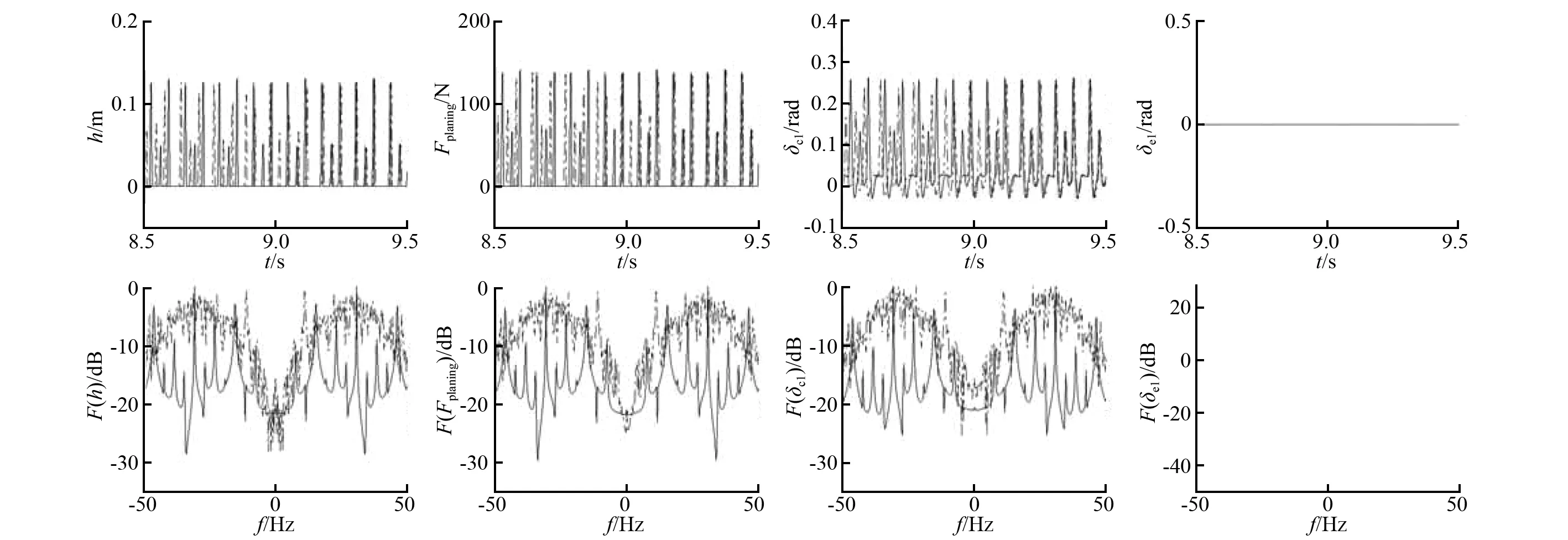
随机选取(σ,k)=(0.030 68, 25.521),当初始值为α1(0.135 2, 0.515 2, 0.261 4, -0.941 5)时,相轨在w-θ平面上的投影如图5(a)所示,形成了一个稳定平衡点。图5(b)为随时间演化的 Lyapunov 指数谱,系统在反馈控制律的作用下迅速进入收敛状态,L4 图4 系统相轨在w-θ平面上的映射 Fig.4 Phase track diagram for diffident parameters 图5 σ=0.030 68, k=25.521时的运动现象Fig.5 Motion phenomenon for σ=0.030 68, k=25.521 图3(b)相对完整地反应了航行体随参数σ、D变化时所处的不同状态,三种颜色代表的三种运动状态呈阶梯式分布,在D取值较小的黑色发散区域中,存在个别的深灰色周期点和白色混沌点,这是由于D过小,不能产生空泡或者产生了部分空泡,航行体几乎在整个空化数有效范围内严重失稳;当D>0.026 2 m时,运动过程中会形成将整个航行体包裹在内的大空泡,航行体全局稳定运动。当D∈[0.010 8, 0.025 7]时,深灰色周期振荡是主要的运动区域,但在σ=0.031 48和σ=0.032 55附近,深灰色区域中穿插着白色混沌点,D的微小变化会引起运动状态在周期与混沌之间的转变;通过仿真计算发现,当该区域中某些系统参数一定时,随机设置初始值的不同会导致航行体具有不同的动力学行为。 随机选择(σ,D)=(0.032 55, 0.019 1),当初始值为β1(1.436 7, -1.960 9, -0.197 7, -1.207 8)时,相轨迹在w-θ平面上的投影如图6(a)所示,出现了极限环,形成了一个周期吸引子。图6(b)为随时间演化的 Lyapunov 指数谱,L1≈0,L4 图6 σ=0.032 55, D=0.019 1时的运动现象 Fig.6 Motion phenomenon for σ=0.032 55, D=0.019 1 2.2.1 空化数对超空泡航行体动力学特性的影响 令D=0.019 1 m,k=0,σ∈[0.019 80,0.036 80],即在经典控制律的作用下,系统随空化数σ变化的分岔情况如图7所示。 当系统处于小空化数σ∈[0.019 80, 0.024 20]时,图7 (a)中的信号点为稳定平衡点,航行体稳定运动。当σ=0.024 25时,发生Hopf分岔,相轨由稳定的有界点突变成极限环,极限环的出现使尾部滑行力开始周期性的变化,系统进入周期轨道。图7(b)是图7(a)在σ∈[0.032 40,0.032 70]的放大,周期轨道经过一系列倍周期分岔,于σ=0.032 46处进入混沌状态,混沌宽带中穿插着多个周期窗,当σ=0.032 70时,混沌宽带突变回2周期轨道,之后,如图7(a)所示,2周期轨道在σ=0.033 96处突变到1周期轨道,航行体开始剧烈的周期振荡甚至倾覆。 图7 系统随σ变化的分岔图 Fig.7 Bifurcation diagram of system for σ 总体来说,此时航行体稳定运动的空化数范围是σ∈[0.019 80,0.024 10],而在空化数的有效范围σ∈ [0.024 20,0.036 80]下无法实现稳定航行,很大程度上限制了航行体的可控性以及稳定性。根据图3(a),在较大的σ范围内,调节k的取值,能够有效实现超空泡航行体的稳定航行,新的控制律有助于提高航行体的可控性和稳定性。 2.2.2 尾翼偏转角对超空泡航行体动力学特性的影响 令σ=0.032 55、D=0.019 1 m,尾翼偏转角δe1=kq,得到系统随k变化的分岔图8,当k<-0.6时,系统发散,此处不做研究。图8(b)是图8(a)在k∈[-0.500,0.500]范围的放大,当-0.500 图8 系统随k变化的分岔图 Fig.8 Bifurcation diagram of system for k 2.2.3 空化器直径对超空泡航行体动力学特性的影响 令k=0、σ=0.030 00,图9为系统运动随空化器直径D变化的分岔图,如图9(a)所示,当D∈[0.015 8, 0.175 2] m时,1周期轨道表明航行体周期振荡,在D=0.017 5 m处,跳变到2周期轨道,图9(b)是图9(a)在D∈ [0.017 7,0.017 9] m范围的放大, 由2周期轨道进入混沌宽带,其间经历较窄的周期窗,然后经过一系列的反倍周期分岔,在D=0.017 9 m附近进入3周期轨道,如图9(a)所示,当D=0.018 3 m时,3周期轨道突变到1周期轨道,随着D的增大,在D=0.022 5 m处发生Hopf分岔,不稳定平衡点演变成稳定平衡点,系统由周期状态突变到稳定状态,之后,图中稳定的平衡点说明系统一直处于稳定状态。在实际工程应用中,可以根据航行体运动特性随空化器直径变化的分岔图,选择合适的空化器直径,避免在非线性现象丰富的空化器直径处取值,以保证航行体的稳定航行。 图9 系统随D变化的分岔图 Fig.9 Bifurcation diagram of system for D 依照Lyapunov稳定性理论可以确定系统动力学行为与任意两个可变参数的对应关系,依照分岔图可以确定系统随任一参数变化而呈现的动力学现象,前一种侧重于为航行体的稳定运动提供参数依据,后一种侧重于研究系统随参数变化的运动规律以及产生的具体非线性物理现象。结合两种理论可以相对完整地分析系统的动力学特性。 表2 不同运动区域的参数取值 按照表2中的A、B、C三点对应的参数取值,随机地选取初始值,系统时域仿真结果和频谱如图10所示,每一个变量的频谱对应在该图的下方,其中虚线、实线和点线分别表示A、B、C点处的运动情况。在A点处,即σA=0.031 20,DA=0.019 1 m,kA=6时,状态变量z、w、θ、q均被吸引到平衡点PA上;浸没深度h=0.014 m,滑行力Fplaning=12.94 N,空化器偏转角δc1=0.054 4 rad,尾翼偏转角δe1=0;频谱能量集中在0频率处。在B点处,即σB=0.028 10,PB=0.018 0 m,kB=0时,四个状态变量均围绕平衡点PB周期振荡;h和Fplaning分别在[0,0.077] m和[0,63.40] N之间周期振荡,δc1在[0.009 9,0.139 6] rad之间周期振荡,航行体尾部不断与空泡壁面发生碰撞;频谱均为多个等间隔的离散尖峰。而在参数取值为σC=0.032 60,DC=0.019 1 m,kC=-0.030的C点处,z、w、θ、q、h、Fplaning、δe1、δc1随着时间变化发生了剧烈的非周期振荡,h最大值为0.380 m,该长度超过了航行体直径,对应的Fplaning在300 N左右,在实际中不可能出现该现象,航行体已倾覆,对应的频域均是宽带连续谱。 (a) z、w、θ、q的时域、频域图 (b) h、Fplaning、δc、δe的时域、频域图图10 A、B、C点处的时域、频域图Fig.10 Time response and frequency domain response for A , B , C point 总的来说,系统参数在A点取值时,由航行体空化器的偏转产生的流体动力以及尾部伸出空泡与流体接触所产生的滑行力来共同维持航行体的平衡,使其处于小攻角斜向运动的稳定状态;参数在B点处取值时,航行体处于周期振荡的运动状态;在C点处,航行体将失稳进而倾覆。由此可知,系统参数对超空泡航行体的运动状态有着至关重要的作用。 系统参数在D点处取值,即σD=0.030 68,DD=0.019 1,kD=25.521时,系统时域仿真结果和频谱如图11所示,每一个变量的频谱对应在该图的下方,虚线表示初始值α1(z0,w0,θ0,q0)=(0.135 2, 0.515 2, 0.261 4, -0.941 5)时,系统四个状态变量、浸没深度,滑行力以及空化器和尾翼偏转角随时间变化的运动情况以及对应的频谱,实线则表示初始值α2(z0,w0,θ0,q0)=(-0.714 5, 1.351 4, -0.224 8, -0.589 0)时,系统各个变量的时域和频域响应情况。 初始值为α1时,在控制律的作用下,状态变量z,w,θ,q迅速稳定在平衡点PD上,h=0.013 m,Fplaning=13.20 N,δc1=0.042 6 rad,δe1=0.092 9 rad,航行体的尾部穿过空泡浸入水中,产生的滑行力与空化器和尾翼提供的升力共同平衡航行体重力,使航行体稳定运动;对应的频谱能量集中在0频处,说明系统很快进入稳定状态,微弱幅度的周期振荡不影响实际的稳定性。 初始值为α2时,随着时间的增大,系统的四个状态变量均减幅振荡,并逐渐向平衡点PD靠拢,直至t=11.02 s附近,z,w,θ,q稳定在PD上;h和Fplaning一开始均为零,在t=10.88 s时突然开始周期振荡,并于t=11.89 s稳定到0.013 m和13.20 N上;δc1减幅振荡并于t=11.22 s稳定在0.042 6 rad上,δe1在t=10.85 s时发生状态转移于t=11.95 s稳定在0.092 9 rad上。可见航行体发射之后,在初始阶段处于小攻角斜向的振荡状态,尾部一直处于超空泡内,随着时间的增加,各个变量均稳定在固定值上,尾部刺破空泡与水接触,航行体的运动由周期状态转移到稳定状态。对应的频谱除在0频外有一对显著的峰值,系统存在较长时间的显著周期振荡。 (a) z、w、θ、q的时域、频域图 (b) h、Fplaning、δc、δe的时域、频域图图11 D点处的时域、频域图Fig.11 Time response and frequency domain response for D point 在E点处,即σE=0.032 55,DE=0.019 1,kE=0,系统时域仿真结果和频域响应情况如图12所示,为了清晰显示航行体运动状态的转移,取t∈[8.50,9.50] s为图示的时间范围。点线表示初始值β1(z0,w0,θ0,q0)=(1.436 7, -1.960 9, -0.197 7, -1.207 8)时,系统四个状态变量、浸没深度,滑行力以及空化器和尾翼偏转角随时间变化的运动情况以及对应的频谱;实线为初始值β2(z0,w0,θ0,q0)=(0.318 8, -1.307 7, -0.433 6, 0.342 6)时系统各个变量的时域、频域响应情况。 当初始值为β1时,z、w、θ、q分别以平衡点PE为中心周期振荡,h的周期性变化为0.126 m、0 m、0.051 m,产生Fplaning对应为138.30 N、0 N、69.22 N,航行体尾部在空泡内外周期振荡;δc1也在平衡点附近周期振荡,k=0,δe1=0;对应的频谱均为多个等间隔的分离尖峰。 当初始值为β2时,在t=9.20 s之前,z、w、θ、q以及h、Fplaning、δc1随时间的变化均发生了剧烈的非周期振荡,t=9.20 s附近,各个变量从非周期振荡突变为周期振荡,之后一直稳定在周期状态,与初始值为β1时的运动状态重合,航行体的运动发生了状态转移,在有限时间尺度内出现的混沌称之为瞬态混沌[14],该现象被称为瞬态混沌稳态周期;对应的频域是宽带连续谱。 通过系统参数在D、E两点取值时超空泡航行体运动状态的分析,不难发现,航行体的运动状态除了随系统参数变化外,还依赖于系统的初始条件,在不同的发射初始条件下,航行体运动状态存在瞬态振荡和运动状态转移的现象。在实际工程应用中,由于水下环境复杂,外界干扰因素多,系统参数一定时,发射初始条件一旦受到外界的微小扰动,航行体就会出现不同的运动状态。考虑到超空泡航行体在水下航行时间较短,针对以上航行体瞬态振荡和运动状态转移的稳定控制,更具有实际工程意义。 (a) z、w、θ、q的时域、频域图 (b) h、Fplaning、δc、δe的时域、频域图图12 E点处时域、频域图Fig.12 Time response and frequency domain response for E point 基于动力学地图、分岔图以及数值仿真等方法,本文研究了多个系统参数对超空泡航行体非线性动力学特性的影响,得到以下结论: (1)随着尾翼偏转角、空化器直径等参数的变化,超空泡航行体系统均会出现分岔、混沌等非线性物理现象。 (2) 超空泡航行体的运动状态不但受系统参数影响,还极端依赖系统的初始条件,在不同的初始条件下发射,航行体会出现不同的运动轨迹,存在瞬态振荡和运动状态转移等非线性运动特性。 (3) 利用动力学地图一方面可以确定航行体稳定运动的参数范围,另一方面也为避开瞬态振荡的参数范围提供了理论依据,从而设置合理的系统参数,抑制航行体的非线性振动与冲击,实现其稳定运动。 [ 1 ] 曹伟,魏英杰,王聪,等. 超空泡技术现状问题与应用[J].力学进展,2006,36(4): 571-579. CAO Wei,WEI Yingjie,WANG Cong,et al.Current status problems and applications of supercavitating technology [J].Advances in Mechanics,2006,36(4): 571-579. [ 2 ] SINGHAL A K,LI H Y,AHAVALE M M,et al.Mathematical basis and validation of the full cavitating high-speed torpedo[J].Journal of Fluids Engineering,2003,125: 459-468. [ 3 ] VANEK B,BOKOR J,BALAS G J,et al.Longitudinal motion control of a high-speed supercavitation vehicle[J].Journal of Vibration and Control,2006,13(2): 159-184. [ 4 ] WANG G,OSTOJA-STARZEWSKI M.Large eddy simulation of a sheet/cloud cavitation on a NACA0015 hydrofoil [J].Applied Mathematical Modeling,2007,31(3): 417-447. [ 5 ] LI Qitao,HE Yousheng,XUE Leiping.A numerical simulation of pitching motion of the ventilated supercaviting vehicle around its nose[J]. Chinese Journal of Hydrodrnamics,2011, 26 (6): 589-685. [ 6 ] 魏英杰,王京华,张嘉钟,等.水下超空泡航行体非线性动力学与控制[J].振动与冲击,2009,28(6): 179-204. WEI Yingjie,WANG Jinghua,ZHANG Jiazhong,et al.Nonlinear dynamics and control of underwater supercavitating vehicle[J].Journal of Vibration and Shock, 2009,28(6): 179-204. [ 7 ] LIN G J,BALACHANDRAN B,ABED E H. Bifurcation behavior of a supercavitating vehicle[C]∥ 2006 ASME international Mechanical Engineering Congress and Exposition. Chicago: ASME, 2006: 5-10. [ 8 ] 白涛,孙尧,莫宏伟.分叉分析在水下高速运动体稳定控制中的应用[J].哈尔滨工程大学学报,2008,29(10): 1067-1075. BAI Tao,SUN Yao,MO Hongwei.Application of bifurcation analysis to the stability control of underwater high-speed vehicles[J].Journal of Harbin Engineering University,2008, 29(10): 1067-1075. [ 9 ] 熊天红,包伯成.超空泡航行体闭环控制动力学特性研究[J].振动与冲击, 2015,34(17): 168-173. XIONG Tianhong,BAO Bocheng.Closed-loop control dynamics for supercavitating vehicles[J].Journal of Vibration and Shock, 2015,34(17): 168-173. [10] 贾力平,王聪,于开平,等.空化器参数对通气超空泡形态影响的实验研究[J].工程力学,2007,24(3): 159-164. JIA Liping,WANG Cong,YU Kaiping,et al.Experimental investigation of cavitator parameters effecting on ventilated supercavity shape[J].Engineering Mechanics,2007,24(3): 159-164. [11] DZIELSKI J,KURDILA A.A benchmark control problem for supercavitating vehicles and an initial inves-tigation of solutions[J].Journal of Vibration and Control,2003,9(7):791-804. [12] LIN G J,BALACHANDRAN B,ABED E H.Dynamics and control of supercavitating vehicles[J]. Journal of Dynamic Control Systems, Measurement, and Control,2008,130(2): 281-287. [13] 包伯成.混沌电路导论[M].北京:科学出版社,2013: 5-38. [14] 包伯成,胡文,许建平,等.忆阻混沌电路的分析与实现[J].物理学报,2011,60(12): 58-65. BAO Bocheng,HU Wen,XU Jianping,et al.Analysis and implementation of memristor chaotic circuit[J].Acta Physica Sinica,2011,60(12): 58-65.


2.2 参数变化对系统动力学的影响分析


3 不同参数下航行体运动状态分析






4 结 论
