大跨径桥梁三维台风风场数值模拟

刘焕举， 韩万水， 武 隽， 肖 强， 闫 利

(1. 长安大学 公路学院，西安 710064；2. 江西省交通设计研究院有限责任公司，南昌 330002；3. 石家庄市三环路管理处，石家庄 050051)

大跨径桥梁由于跨径较大，较多采用悬索或斜拉的结构形式，具有塔高、质轻和阻尼弱等特点，对风作用十分敏感，开展风环境下的桥梁安全评估有重要意义。台风风速较大，且风速变化较快，对处于台风频发区域的大跨桥梁，其安全性更应特别关注。台风作用下的大跨桥梁安全评价，台风风场的合理模拟是面临的首要问题。

目前针对桥梁等工程结构物尺寸的台风风场模拟研究主要分为两类：①改变经典风谱中的参数模拟台风[1]；②采用进化谱方法对台风进行模拟。由于基于经典风谱模拟的风速是平稳的，而台风风速具有明显的非平稳特性，该方法的误差较大，对台风风场模拟不太适用。而采用进化谱的模拟方法则可进一步细分为两种：均匀调制进化谱方法[2-3]和非均匀调制进化谱[4-5]方法。均匀调制进化谱是将与时间、频率均有关的非均匀调制函数设为仅与时间有关的均匀调制函数，虽然降低了模拟难度，但同时也降低了模拟精度，尤其是对风作用十分敏感的大跨桥梁，应采用非均匀调制进化谱方法进行风场模拟。但目前采用非均匀调制进化谱方法对风的模拟研究主要集中于下击暴流产生的非平稳风，针对台风的较少，下击暴流为雷暴天气中强烈的下沉气流猛烈撞击地面，并由撞击点向四周沿地表传播的极具突发性和破坏性的一种强风，与台风在形成原因及物理特性等方面不同，下击暴流产生的非平稳风模拟方法可为台风模拟提供借鉴，而不能直接应用于台风模拟。李锦华等[6]针对非平稳风，基于进化谱理论，推导得到了非平稳风的进化谱，在假设非平稳风时变平均风速服从余弦规律的基础上，对不同高度的点进行了非平稳风场的模拟。但模拟过程中只考虑了高度方向相关性，未考虑时变平均风速随风剖面的变化及各模拟点的空间相关性。因此，在已有的非平稳风研究基础上，开展考虑空间相关性的三维台风风场模拟方法研究十分必要。

本文首先构建三维台风风场模拟方法，利用三次样条函数，获取台风时变平均风速，并采用更新时变平均风速的谐波合成法实现台风脉动部分的模拟。其次提出用于验证三维台风风场的进化谱。最后选取某沿海大跨斜拉桥为例，应用构建的三维台风风场模拟验证方法，进行三维风场的模拟，并对模拟结果进行验证。

1 三维台风风场模拟

台风在水平方向上一般可分为台风外围、台风本体和台风中心三部分，台风外围和本体的直径都在200 km以上，即使是最内侧的台风中心到台风眼，半径一般也在20～60 km，桥梁尺度与之相比很小，因此在台风风场模拟时，忽略沿桥梁跨度方向上的台风方向和平均风速的变化。台风风速是一个源于时变均值、时变方差的极端事件，风速变化较快，且具有明显的非平稳特性。目前关于台风风场的模拟研究[7]，一般把台风风速模拟分为平均风速模拟和脉动风速模拟两个部分，其中平均风速模拟多采用时变平均风速形式，脉动部分风速的模拟则采用多个足够短时间段内的零均值平稳脉动风速形式，台风风速模型为

U0(t)=U(t)+u(t)

(1)

式中：U0(t)为t时刻台风风速；U(t)为时变平均风速；u(t)为脉动风速。

1.1 平均风剖面模型

对台风三维风场进行模拟时，平均风剖面模型的研究十分重要。平均风剖面模型有指数律模型、对数律模型及D-H模型等，根据已有的台风风剖面的研究[8-11]结果，台风平均风速随高度的变化规律宜采用指数函数来进行描述，尤其是对于粗糙度较小的地表状况，拟合效果更好。指数函数风剖面经验模型

(2)

式中：Uz为z高度处的平均风速；Uz1为z1高度处的平均风速；α为地表粗糙度系数。

1.2 时变平均风速模拟

在已有的台风模拟研究中，对时变平均风速的获取方法主要分为三种：①假定时变平均风速为一常数；②假定时变平均风速服从已知函数，如余弦函数；③从实际台风风速时程曲线中提取[12]。以上三种方法虽然都能获取台风时变平均风速，但由于台风具有明显的非平稳特性，风速变化较快，不同台风由于物理特性不同，风速规律也有较大差别，所以时变平均风速为一常数或服从某确定函数曲线的假定不太适用。而基于实测的台风风速时程曲线，通过EMD(Empirical Mode Decomposition)等分解方法提取台风时变平均风速的方法，虽然准确度高，可信度强，但多用于已知台风风速时程，对台风风速特性进行分析，而且目前的台风资料中，多是已知台风经过区域某测点多个时间间隔T0(T0为15 min，1 h或6 h等)的平均风速点，所以应用也不广泛。如何利用已知的多个较长时间间隔(如15 min等)的台风平均风速对台风时变平均风速进行模拟，是台风风速模拟面临的首要问题。

样条插值是一种工业设计中常用的、用以得到平滑曲线的一种插值方法，三次样条又是其中应用较为广泛的一种。考虑到曲线的平滑性和风速变化率的连续性，本文采用三次自然样条曲线插值方法对台风时变平均风速进行模拟。具体如下：以实测n个时间间隔为T0的平均风速点为型值点，编制Matlab程序，构筑允差为0的三次样条曲线，并把该样条曲线离散成p个足够短时间间隔Δt的时间序列，p=nT0/Δt。由于时间间隔Δt足够短， 每个Δt对应的样条曲线段上任意时间点的平均风速均可视为该时间间隔内的平均风速，即为时变平均风速，例如在t～t+Δt内， 时变平均风速可表示为U(t)。 通过上述方法，实测n个时间间隔为T0的平均风速转换成为p个足够短时间间隔Δt的时变平均风速序列，即为时变平均风速。

1.3 脉动风速模拟

良态风脉动部分一般基于经典功率谱，采用谐波合成法进行模拟。但台风风速与良态风风速相比，其风速变化较快，平均风速的时变性也较为明显，具有典型的非平稳特性，因此对台风脉动风速进行模拟时，对谐波合成法进行了相应改进：把模拟时长离散成p个足够短时间间隔Δt， 因为Δt足够短， 每个Δt内的风速均可近似视为平稳随机过程，采用谐波合成法对脉动风速进行模拟，对不同的时间间隔，则通过更新每个时间间隔Δt内的经典功率谱中的时变平均风速，实现台风风速的非平稳特性，对台风风速进行精确模拟。台风脉动风速模拟具体分为两步：①在每个足够短的时间间隔Δt内，采用谐波合成法模拟零均值稳态脉动风速，实现每个足够短的时间间隔Δt内的脉动风模拟；②在不同时间间隔中，随着时变平均风速变化更新风功率谱，实现不同时间间隔内的脉动风速模拟。

步骤1每个时间间隔Δt内的脉动风速模拟。

由于Δt足够短， 每个时间间隔Δt内的时变平均风速U(t)可视为常数，脉动风速也可视为零均值平稳随机过程，因此可直接采用良态风脉动风速的模拟方法——谐波合成法对每个时间间隔内的台风脉动风速进行模拟。

下面以z高度处的节点i(i=1,2,…,m)为例， 对节点i在t～t+Δt内的脉动风速进行模拟。

在已有的风场模拟研究中，水平顺风向风谱和横风向风谱常采用Simiu谱[13]，竖向风谱采用Lumley-Panofsky谱[14]。则该时间间隔t～t+Δt内的风谱为

(3a)

(3b)

(3c)

作用于桥梁不同节点位置处的脉动风，在空间上存在相干性，这种相干性通常表示为节点空间距离的函数，即为相干函数，表示为Coh(ω,t)，本文根据已有的台风相关性研究结果[15]，不同节点处的台风相干函数采用Davenport形式[16]

(4)

式中：ω为圆频率；D为计算点之间的空间距离；λ为衰减系数，取7。

由于三个方向的风场模拟方法相同，为论述方便，选取水平顺风向风场为例，对模拟方法和步骤进行具体阐述，功率谱密度函数采用S(f)表示。

由于Δt足够短，每个时间间隔Δt内的时变平均风速U(t)视为常数， 则在时间间隔t～t+Δt内的台风脉动风速可视为一个零均值的一维m变量平稳高斯过程{ui(t)}，其互谱密度矩阵为

(5)

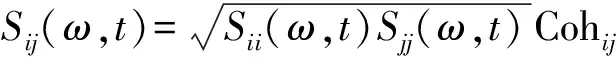
在每个时间间隔Δt内， 对S(ω,t)进行Cholesky分解

S(ωjk,t)=H(ωjk,t)HT*(ωjk,t)

(6)

式中，HT*(ωjk,t)为H(ωjk,t)的复共轭转置矩阵；S(ω,t)为双边功率谱。

根据Shinozuka-Deodatis理论[17-18]，该时间间隔内的各模拟点的脉动风速时程可表示为

(7)

(8)

θij(ωjk,t)为Hij(ωjk,t)的复角， 表示为

(9)

为了避免模拟结果失真现象，时间增量必须满足一下关系式

(10)

模拟的随机过程的周期为

(11)

步骤2不同时间间隔内的脉动风速模拟。

台风风速变化较快，不同时间间隔内的时变平均风速差异较大，因此在模拟不同时间间隔内的台风脉动风速时，需通过更新式(3)经典风谱中的时变平均风速，得到每个时间间隔内的时变风功率谱，然后采用步骤1，对不同时间间隔内的三个方向上的脉动风速进行模拟。

在分别实现台风时变平均风速和水平顺风向脉动风速的模拟的基础上，依据式(1)，取台风时变平均风速与相应时间间隔内的水平顺风向脉动风速之和，即实现了台风风速的模拟。

2 台风风场验证——进化谱

良态风风场的模拟一般通过功率谱进行验证，但台风风速变化较快，与良态风风速相比，非平稳特性较为明显，对非平稳随机过程可采用进化谱进行验证。本文基于经典风功率谱密度函数，采用非均匀调制函数对经典功率谱进行调制，构建进化谱，进而对模拟的台风三维风场进行验证。

下面以时间间隔t～t+Δt内的脉动风谱为例，推导该时间间隔内的进化谱。

在时间间隔t～t+Δt内，相应于水平顺风向脉动风Kaimal谱的与时间频率有关的非均匀调制函数为

(12a)

相应的竖向和水平横风向功率谱的非均匀调制函数分别为

(12b)

(12c)

在时间间隔t～t+Δt内的进化谱G(ω,t)为

G(ω,t)=A2(ω,t)S(ω)

(13)

式中，S(ω)为功率谱密度函数，由式(3)转化得到，表达式为

(14a)

(14b)

(14c)

将整个模拟时长nT0内的各个时间间隔的进化谱按时间序列集成起来，构成整个模拟时长内的进化谱，进化谱为时间t和频率ω的函数，为实现对模拟台风风速的验证，把进化谱化为频率ω的函数为

(15)

式中，GnT0(ω)为用于台风模拟验证的进化谱。

3 实例分析

3.1 工程背景

3.1.1 桥梁概况及模拟点选取

本文选取杭州湾某大跨斜拉桥为工程实例，应用构建的三维台风风场模拟方法，进行三维台风风场的模拟。该大跨斜拉桥设计跨径为908 m，为钻石型双塔空间双索面五跨连续钢箱梁斜拉桥，其中主桥索塔高181.3 m，如图1所示。气象调查显示该桥桥位所处于的杭州湾气象复杂多变，台风、雷暴等突发性灾害天气时有发生，仅2015年就遭受了“灿鸿”、“杜鹃”、“苏迪罗”等一系列台风。

对全桥三维风场的模拟，选取了18个典型的模拟点：其中沿跨度方向选取了10个点，各点间距为：4×101 m+100 m+4×101 m；每个桥塔沿塔的高度方向各选取了4个点，具体为：桥面与墩底的中点处、塔顶点及沿塔顶向下间隔均为60 m的两个点。模拟点布置如图1所示。

图1 实例桥梁立面图及台风模拟点布置(单位：m)Fig.1 Elevation and typhoon simulation point location of example bridge (unit:m)

3.1.2 参数的选取

在三维台风风场模拟时，风剖面采用指数律模型。该桥位于杭州湾开阔水面上。桥梁的抗风规范中，当地表状况为A类，即海面、海岸、开阔水面时，地表粗糙度系数α=0.12，但该幂指数的取值是基于大量实测风速，且兼顾大小不同的风速情况，通过拟合得到的。台风是一个对流活动较为强烈的热带低气压，在台风环流内，水平风速较大导致气流的对流运动较强，上下层气流的动能就能够进行充分交换，使得上下层气流的风速差别较小，从而使风速廓线的指数也相对变小，因此在台风模拟时，α取值不能直接套用抗风规范中的0.12。在已有的台风风剖面的研究中，通过台风实测数据分析，得出当地表状况为开阔水面时，地表粗糙度系数α的取值范围为：0.06～0.10，为安全考虑，α=0.10。台风模拟计算的其它主要参数如下：跨度L=908 m，主梁跨中点离地高度z=54 m；地面粗糙度z0=0.01；模拟点数m=18；截止频率；ωup=4π rad/s； 频率等分数N=1 024； 模拟采样时距dt=0.5 s；目标谱采用式(15)表达的进化谱G(ω)。

3.1.3 台风平均风速数据的选取

由于缺少桥址处的台风数据，本文采用已知的台风数据——典型台风Wilma后眼壁部分的实测数据。台风Wilma是大西洋上出现的最强台风之一，2005年10月17日在加勒比海域发展形成，于2005年10月24日在佛罗里达登陆。本算例的台风平均风速来自于佛罗里达大学采用便携式装置塔系统采集的台风Wilma数据。台风平均风速随时间不断变化，且采集的平均风速时间间隔为15 min，若选取较短时间(小于15 min)的台风平均风速数据，台风平均风速变化幅度较小，为得出台风风速的规律性，选取较长时间段(90 min)的台风平均风速数据。选取台风Wilma 2005年10月24日09:00～10:45平均风速数据(http://fcmp.ce.ufl.edu)，风速采集仪离地高度10 m，平均风速采集计算时间间隔为15 min，共7个平均风速数据，模拟时取中间5个平均风速数据，时间跨度为4 500 s(450～4 950 s)，即模拟时长为4 500 s，采用三次样条曲线把数据点连接起来，如图2所示。该时段的统计平均风速为22.66 m/s。

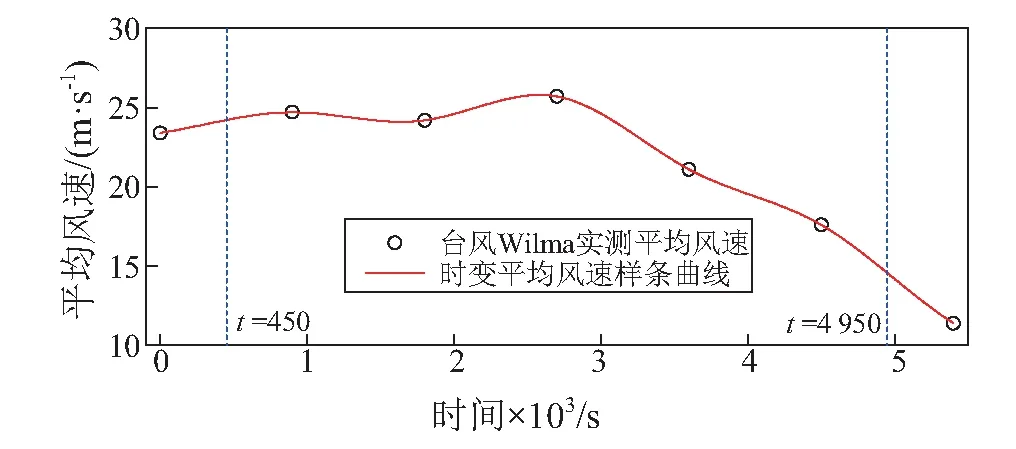
图2 台风Wilma实测平均风速Fig.2 The measured average wind speed of Wilma

3.2 三维台风风场数值模拟

基于第1.2节中台风时变平均风速的获取方法，把图2中时间跨度为4 500 s(450～4 950 s)的三次样条曲线离散成9 000个时间间隔Δt=0.5 s的时变平均风速序列，在每个时间间隔内采用第1.3节中的谐波合成法实现该时间间隔内的脉动风速的模拟，最后将时变平均风速与相应的脉动风速相加，实现台风风速的模拟。限于篇幅，仅给出部分典型模拟点的风速模拟结果，选出的典型点为分布在主梁和桥塔(见图1)的第5点、第11点、第13点和第14点，第5点给出了三个方向风场的模拟结果，第11点、第13点和第14点给出了风速和水平顺风向的脉动风速。模拟结果如图3所示。

由图3可以看出，台风风速总体变化趋势与时变平均风速变化趋势相同，台风风速时程曲线在时变平均风速曲线两侧上下波动。在任一模拟点处，台风脉动风速的波动幅度与时变平均风速有相关关系，时变平均风速越大，脉动风速的波动幅度越大，反之亦然。主梁水平方向上的各模拟点，由于高程相近，脉动风波动幅度与风速大小均相近。沿桥塔垂直方向上的各模拟点，随着高程增加，脉动风波动幅度变小，减小趋势在高程较低时较为剧烈，而后较为缓慢，且随着高程增加，风速随着时变平均风速的增大而不断增大。

图3 各模拟点的脉动风速和风速时程Fig.3 Time history of wind speed and fluctuating wind speed of simulation point

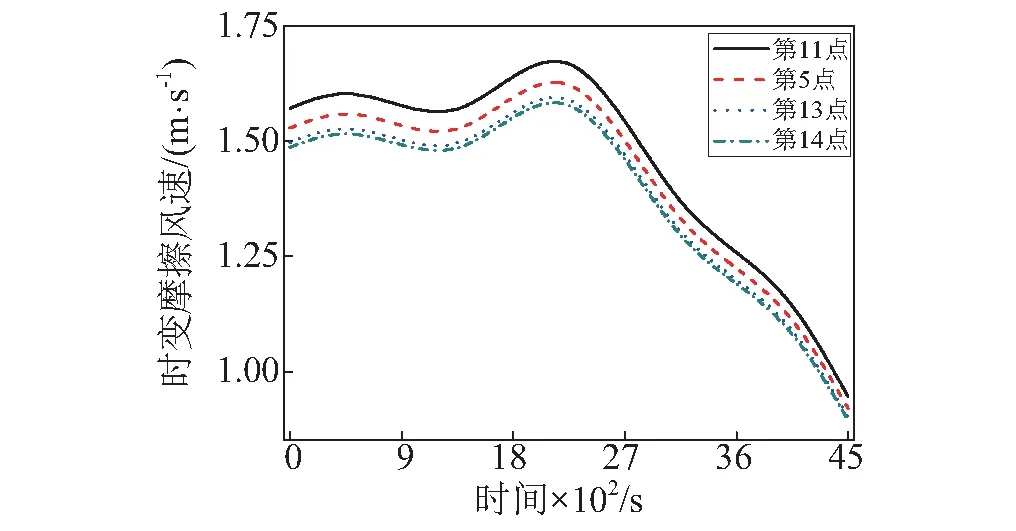
图4 各典型模拟点摩擦风速Fig.4 Friction wind velocity of typical simulation points

由式(3)可知，随着摩擦风速的增大，功率谱密度函数增大，风能量增强，进而脉动风的波动幅度会变大。沿主梁水平方向的各模拟点，由于高程相近，摩擦风速和时变平均风速也相近，因此脉动风波动幅度和风速都较为相近。沿桥塔垂直方向上的各模拟点，高程相差较大，各点的摩擦风速如图4所示。摩擦风速在塔底时较大，随着高程增加，减小趋势先剧烈后缓慢，在高程大于60 m时，随高程变化非常缓慢，因此，塔底模拟点的脉动风速波动幅度较大，桥塔上的另外三个模拟点脉动风波动幅度较小，且差别不大。由式(2)可知，随着高程增加，平均风速呈指数增长，因此沿桥塔垂直方向的各模拟点的时变平均风速，随高程增大而不断增大。

3.3 三维台风风场数值模拟验证

对模拟的台风风速通过FFT等过程，获取各模拟点模拟功率谱，并通过编制程序计算相应的进化谱，对比模拟功率谱和进化谱，验证风场模拟的合理性。图5给出了第5点三向风场的模拟功率谱与进化谱的对比图和第11点、第13点及第14点的水平顺风向模拟功率谱与进化谱对比图。

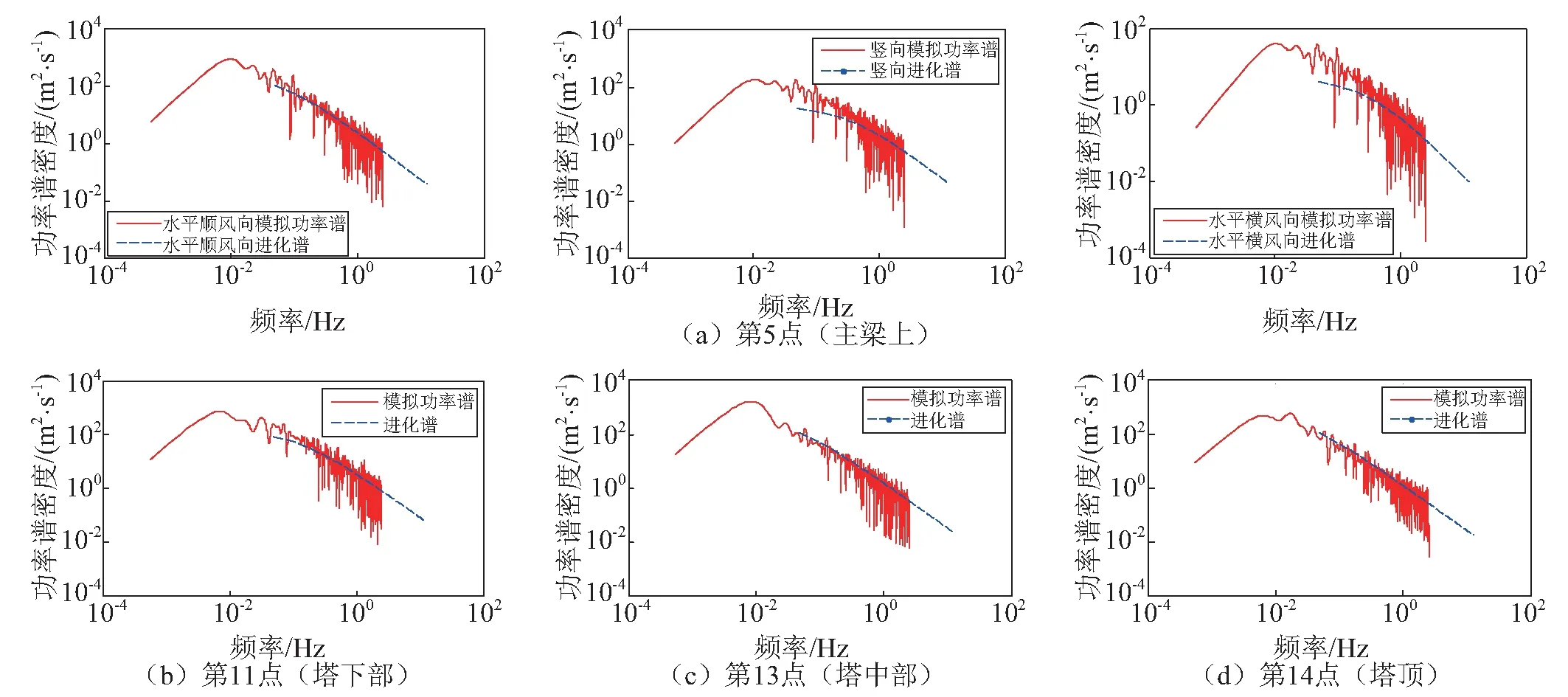
图5 各模拟点的模拟功率谱与进化谱对比Fig.5 Comparison the spectrum of simulation typhoon field and evolutionary spectrum of simulation point

由图5可知，第11点功率谱密度较大，其余各模拟点的功率谱密度函数较为接近，这主要是由于第11点的高程较低，摩擦风速较大，脉动风波动幅度较大，能量较强，其余各模拟点的摩阻风速较为接近，脉动风速的波动幅度也较为接近，功率谱密度函数相差不大。各模拟点的模拟功率谱与进化谱除在非常低的频率点上有差别，在绝大部分上吻合度都很好。对于大跨桥梁，低频风速对桥梁的振动影响很小，因此当模拟结果应用于桥梁评估时，完全满足要求。

4 结 论

本文考虑台风风场的非平稳特性和模拟点群的风速相关性，提出基于改进谐波合成法的三维台风风场模拟方法，并基于进化谱理论，构建进化谱，并选取实例进行了模拟方法的应用。研究表明：

(1) 把模拟时长离散成足够短时间间隔，改进谐波合成法，通过更新每个时间间隔内的平均风速，可实现台风风速的非平稳特性。

(2) 模拟点的高程和时变平均风速对脉动风速的波动幅度影响较大。随高程的增加，台风脉动风速的波动幅度呈先剧烈后缓慢的减小趋势，高程相近时，各模拟点的脉动风速波动幅度相近。时变平均风速较大时，脉动风速的波动幅度较大，反之亦然。功率谱密度与脉动风波动幅度具有相同的规律。

(3) 基于进化谱理论，三维台风风场模拟的合理性可用进化谱来进行检验。考虑各模拟点风速的空间相关性，选用指数律的风剖面模型，采用改进的谐波合成法模拟的台风风场功率谱与构建的非均匀调制进化功率谱吻合很好，模拟结果合理，模拟方法有效。

(4) 采用谐波合成法，在每个频率点都要进行一次Cholesky分解，计算量较大，对风速时间上的相关性也考虑不足，优化算法的研究有待于进一步开展。各点之间风速的空间相关性研究虽已经开展，但参数研究结论还未达成一致，基于实测风速的空间点群风速相干函数的研究也有待于进一步深化。

[ 1 ] LI X L, XIAO Y Q, KAREEM A, et al. Modeling typhoon wind power spectra near sea surface based on measurements in the south China sea[J].Journal of Wind Engineering and Industrial Aerodynamics,2012,(104/105/106): 565-576.

[ 2 ] 李春祥,刘晨哲,申建红,等. 土木工程下击暴流风速数值模拟的研究[J].振动与冲击,2010,29(12): 49-54.

LI Chunxiang, LIU Chenzhe, SHEN Jianhong, et al. Numerical simulations of downburst wind speeds in civil engineering[J]. Journal of Vibration and Shock, 2010,29(12): 49-54.

[ 3 ] 张文福,谢丹,刘迎春,等. 下击暴流空间相关性风场模拟[J].振动与冲击,2013,32(10): 12-16.

ZHANG Wenfu, XIE Dan, LIU Yingchun, et al. Simulation of downburst wind field with spatial correlation[J]. Journal of Vibration and Shock, 2013,32(10):12-16.

[ 4 ] 李锦华,吴春鹏,陈水生. 下击暴流非平稳脉动风速数值模拟[J].振动与冲击,2014,33(14): 54-60.

LI Jinhua, WU Chunpeng, CHEN Shuisheng. Simulation of non-stationary fluctuating wind velocity in downburst[J]. Journal of Vibration and Shock, 2014,33(14): 54-60.

[ 5 ] HUANG G Q, ZHENG H T, XU Y L, et al. Spectrum models for nonstationary extreme winds[J]. Journal of Structural Engineering, 2015, 141(10): 1-12.

[ 6 ] 李锦华, 李春祥, 申建红. 非平稳脉动风速的数值模拟[J]. 振动与冲击,2009,28(1): 18-23.

LI Jinhua, LI Chunxiang, SHEN Jianhong. Simulation of non-stationary fluctuating wind velocity[J].Journal of Vibration and Shock,2009,28(1): 18-23.

[ 7 ] ZHANG W. Bridge fatigue damage assessment under vehicle and non-stationary hurricane wind[C]//The 12th Americas Conference on Wind Engineering. Washington: ACWE, 2013.

[ 8 ] HU L, XU Y L. Extreme value of typhoon-introduced non-stationary buffeting response of long-span bridges[J]. Probabilistic Engineering Mechanics,2014, 36(2): 19-27.

[ 9 ] 王旭, 黄鹏, 顾明. 台风“梅花”近地风剖面变化[J]. 同济大学学报(自然科学版),2013,41(8): 1165-1171.

WANG Xu, HUANG Peng, GU Ming. Variation of wind profiles near ground during typhoon “Muifa”[J]. Journal of TongJi University (Natural Science),2013,41(8): 1165-1171.

[10] 徐家良, 穆海振. 台风影响下上海近海风场特性的数值模拟分析[J]. 热带气象学报,2009,25(3):281-286.

XU Jialiang, MU Haizhen. Numerical simulation and analysis of offshore wind field features in Shanghai under the influence of typhoon[J]. Journal of Tropical Meteorollgy, 2009,25(3): 281-286.

[11] 李利孝, 肖仪清, 宋丽莉, 等. 基于风观测塔和风廓线雷达实测的强台风黑格比风剖面研究[J]. 工程力学,2012,29(9):284-293.

LI Lixiao, XIAO Yiqing, SONG Lili, et al. Study on wind profile of typhoon hagupit using wind observed tower and wind profile radar measurements[J]. Engineering Mechanics,2012,29(9): 284-293.

[12] CHEN J, XU Y L. On modeling of typhoon-induced non-stationary wind speed for tall buildings[J].The structural Design of Tall and Special Buildings,2004,13(2): 145-163.

[13] HUANG G Q, ZHENG H T, XU Y L, et al. Spectrum models for nonstationary extreme winds[J]. Journal of Structural Engineering, 2015.

[14] 李永乐. 风-车-桥系统非线性空间耦合振动研究[D].成都：西南交通大学，2003.

[15] CAO S Y, TAMURA Y K, KIKUCHI N S, et al. Wind characteristic of a strong typhoon[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009,97(1): 11-21.

[16] DAVENPORT A G. Gust loading factors[J].Journal of the Structural Division,1967,93(3): 11-34.

[17] SHINOZUKA M, JAN C M. Digital simulation of random processes and its applications[J]. Journal of Sound and Vibration,1972,25(1): 111-128.

[18] DEODATIS G. Simulation of ergodic multivariate stochastic processes[J]. Journal of Engineering Mechanics, 1996,122(8): 778-787.