Dynamic Analysis of Non-Symmetric Functionally Graded (FG)Cylindrical Structure under Shock Loading by Radial Shape Function Using Meshless Local Petrov-Galerkin (MLPG) Method with Nonlinear Grading Patterns

Y. Sadeghi Ferezghi , M.R. Sohrabi and S.M Mosavi Nezhad

1 Introduce

Dynamic analyses of cylindrical structure are one of the important engineering problems.In order to optimize the displacements and stresses of structures subjected to loads, is often used Functionally Graded Materials (FGMs) in cylindrical structure. In this paper, the material properties of FGM are defined by nonlinear grading patterns. Stress analysis in a 2D-FGM thick finite length hollow cylinder was studied by Najibi and Shojaeefard [Najibiand Shojaeefard (2016)]. Khosravifard et al. [Khosravifard, Hematiyan and Marin(2011)]focused on nonlinear transient heat conduction analysis of functionally graded materials.Vibration characteristics of FGM cylindrical shells resting on Pasternak elastic foundation were investigated by Park and Kim [Park and Kim (2016)]. Shen et al. [Shen, Paidoussis and Wen et al. (2014)] proposed the beam-mode stability of periodic functionally graded material shells conveying fluid. Vibration analysis of a functionally graded hollow cylinder has been studied by Chen et al. [Chen, Bian and Ding (2004); Chen, Bian and Lv et al. (2004)]. Hosseini et al. [Hosseini and Abolbashari (2010); Hosseini, Akhlaghi and Shakeri (2007)] carried out dynamic analysis of functionally graded thick hollow cylinders.Stochastic wave propagation in functionally graded materials was studied by Hosseini and Shahabian [Hosseini and Shahabian (2011); Hosseini and Shahabian (2011)].

In recent decade, Meshless method as a new numerical method has been proposed[Jaberzadeh and Azhari (2015); Mirzaei and Hasanpour (2016); Sladek, Sladek and Atluri(2004); Sladek, Stanak and Han et al. (2013); He and Seaid (2016); Tadeu, Stanak and Antonio et al.(2015)]. Meshless Local Petrov-Galerkin (MLPG) method has become a very useful and effective solving method in structures made of Functionally Graded Materials (FGMs) because these materials have variable mechanical properties and this method doesn’t require to the mesh generation on the domain, therefore we can continuously model these materials with this method. Lin and Atluri [Lin and Atluri (2000)]studied Meshless Local Petrov-Galerkin (MLPG) Method for convection-diffusion problems. They, proposed several up winding schemes, and applied to solve steady convection diffusion problems, in one and two dimensions. Meshless Local Petrov-Galerkin (MLPG) method in combination with finite element and boundary element approaches was investigated by Liu and Gu [Liu and Gu (2000)]. Zhang et al. [Zhang,Song and Liu et al. (2000)] carried out meshless methods based on collocation with radial basis functions. They showed that the accuracy of derivatives of interpolating function are usually very poor on boundary of domain when a direct collocation method is used, with Neumann boundary conditions. Analysis of thick plates by using a higher-order shear and normal deformable plate theory and MLPG method with radial basis functions was proposed by Xiao et al. [Xiao, Batra and Gilhooley et al. (2007)]. They analyzed infinitesimal deformations of a homogeneous and isotropic thick elastic plate. They employed Radial Basis Functions (RBF) for constructing trial solutions and two types of RBFs, multiquadrics (MQ) and Thin Plate Splines (TPS), are employed and effects of their shape parameters on the quality of the computed solution are examined for deformations of thick plates under different boundary conditions. Rezaei Mojdehi et al. [Rezaei Mojdehi,Darvizeh and Basti et al. (2011)] investigated 3D static and dynamic analysis of thick functionally graded plates by the Meshless Local Petrov-Galerkin (MLPG) method. In their work, using the kinematics of a three dimensional continuum, the local weak form of the equilibrium equations is derived. A weak formulation for the set of governing equations is transformed into local integral equations on local sub-domains using a Heaviside step function as test function. Analysis of the bending of circular piezoelectric plates with functionally graded material properties by a MLPG method was studied by Sladek et al. [Sladek, Sladek and Stanak et al. (2013)]. In their work, material properties are considered to be continuously varying along the plate thickness, also the axial symmetry of geometry and boundary conditions for a circular plate reduces the original three-dimensional (3-D) boundary value problem into a two-dimensional (2-D) problem.Zhao et al. [Zhao, Liu and Dai et al.(2008)] carried out geometric nonlinear analysis of plates and cylindrical shells via a linearly conforming radial point interpolation method.In their paper, the Sander’s nonlinear shell theory is utilized and the arc-length technique is implemented in conjunction with the modified Newton-Raphson method to solve the nonlinear equilibrium equations. The radial and polynomial basis functions are employed to construct the shape functions with Delta function property using a set of arbitrarily distributed nodes in local support domains. Foroutan and Moradi [Foroutan and Moradi-Dastjerdi (2011)] investigated dynamic analysis of functionally graded material cylinders under an impact load by a mesh-free method. In this analysis, Moving Least Square (MLS)shape functions are used for the approximation of the displacement field in the weak form of motion equation and essential boundary conditions are imposed by the transformation method. The resulting set of time domain differential equations is solved using central difference approximation. Dynamic analysis of functionally graded nanocomposite cylinders reinforced by carbon nanotube by a mesh-free method was proposed by Moradi et al. [Moradi-Dastjerdi, Foroutan and Pourasghar (2013)]. In their paper presented free vibration and stress wave propagation analysis of carbon nanotube reinforced composite(CNTRC) cylinders. In this simulation, an axisymmetric model is used. Material properties are estimated by a micro mechanical model. Moving Least Squares (MLSs) shape functions are used for approximation of displacement field in the weak form of motion equation and the transformation method was used for the imposition of essential boundary conditions.

In this paper, dynamic equation of non-symmetric FG cylindrical structure is drawn out using Meshless Local Petrov-Galerkin (MLPG) method. The displacements can be approximated using shape function so that we choose radial functions as the basis in equation. The dynamic behaviors of non-symmetric FG cylindrical structure in time domain obtained with Meshless Local Petrov-Galerkin (MLPG) method is combining with Laplace transform method. The MLPG obtained results compare with analytical and Finite Element Method (FEM). Finally, the non-symmetric FG cylindrical structure is analyzed under harmonic and rectangular shock loading.

2 MLPG implementation

Governing dynamic equations of cylindrical structures with asymmetric geometry and boundary conditions in polar coordinates can be written as follows:

where "ρ(r)" is the mass density, "σr", "σθ" and "τrθ" are radial, hoop and shear stresses respectively. The terms "ur" and "uθ" denote the radial and hoop displacement,respectively.

In this paper, cylindrical structure made of FGM, and also FG material in this structure is graded through the r-direction. Material properties of FG cylindrical structures can be defined as

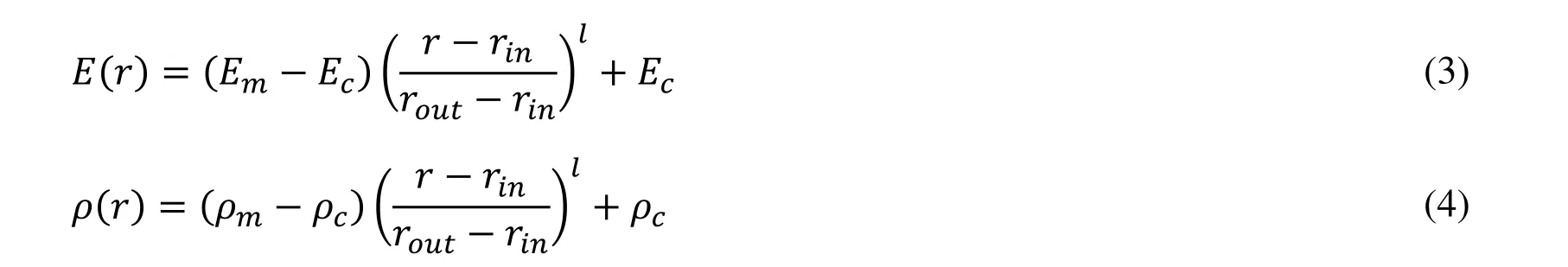
where "l" is a non-negative volume fraction exponent, subscript "m" and "c" stand for metal and ceramic material, "E" and "ρ" are modulus of elasticity and mass density,respectively. Constitutive equations for FG cylindrical are

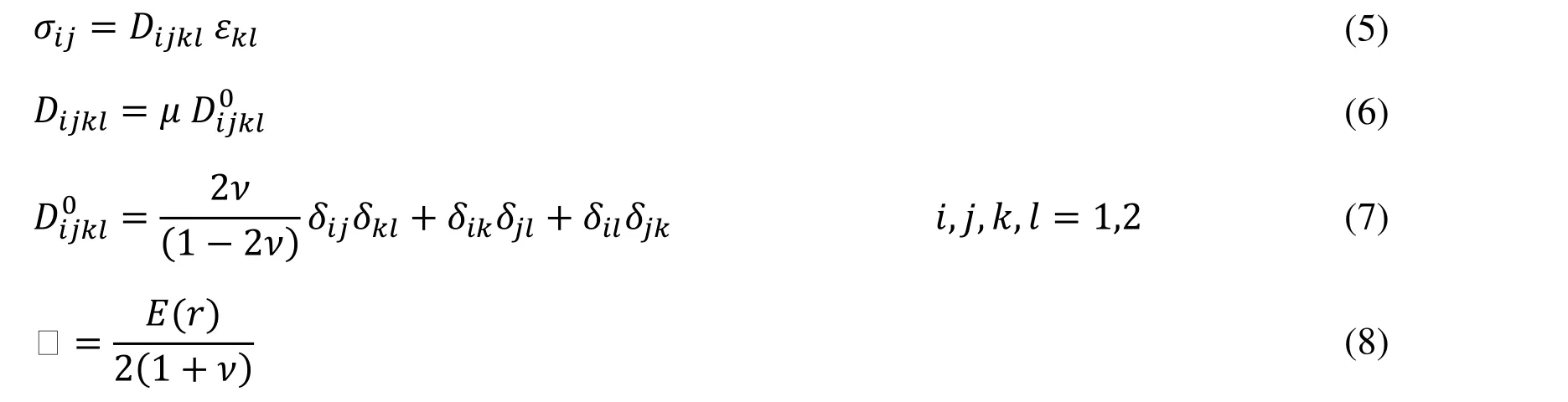
where "δij" is Kronecker delta and "ν" is Poisson's ratio. The strain-displacement relations are given by

where "εr", "εθ" and "γrθ" are radial, hoop and shear strain, respectively. In the analysis of non-symmetric cylindrical structures, for converting points from Cartesian coordinates into cylindrical coordinates is used

By using equation (12) we developed the weak-form over a local subdomain "ΩQ" instead of constructing the global weak-form for whole domain of dynamic problem. So, we have

where "WI" is the weight function. The divergence theory is employed for equations (13)and (14) as follows, which "ΩQ" and "ΓQ" are quadrature domain and boundary of quadrature domain, respectively.

where "nr" and "nθ" are the unit outward normal vector on the boundary for "r" and "θ"direction, respectively. The boundary of quadrature domain is divided to some parts as"ΓQ= ΓQi∪ ΓQu∪ ΓQt". The term "ΓQi" is the internal boundary of the quadrature domain,"ΓQu" is the part of the essential boundary that intersects with the quadrature domain and"ΓQt" is the part of the natural boundary that intersects with the quadrature domain (see Fig. 1).

Figure 1: The domain and the boundary of cylindrical structure in MLPG method

We can then change the expression of equations (15) and (16) to

where "tr" and "tθ" are the radial and hoop tractions, respectively and they are defined as follows:

The matrix form of equations (17) and (18) is given as:

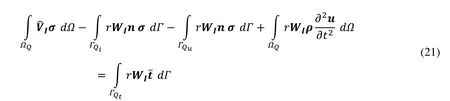
The displacements can be approximated using shape function. Shape function defined for each point using the nodes in support domain "Ωs" of a point (see Fig. 1). In this paper,we used the Radial Point Interpolation Method (RPIM) shape function, the advantage of using this shape function is its simplicity and high accuracy. We choose radial functions as the basis in equation

The matrix form of equations (27) and (28) can be stated as

Furthermore, shape function "φ(r̅)" defined as follow:

The vector "R" and matrix "RQ" can be written:

There are a number of forms of radial basis functions used by the mathematics community.In this paper we used the type of a classical form is called multiquadric (MQ) basis. The MQ basis function is following

where "C" and "q" are constant coefficient.

Substitution of the equation (5) and (29) into equation (21) gives

where "k" is the number of nodes. Matrix "D" and "B" defined as follow:

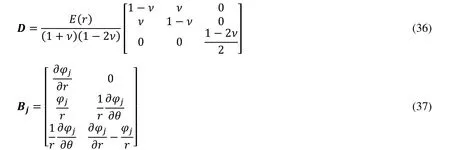
There are some numerical techniques to solve the governing equations in time domain. In this article, Laplace transform is used for time domain analysis with the initial conditions that are assumed to be zero.

The time-dependent values of transformed of the quantities in the previous consideration can be obtained through an inverse Laplace transform. There are many inversion methods available for inverse Laplace transform. In the present analysis, the Talbot algorithm for the numerical inversion is used. The Talbot inversion formula to numerically calculate for"uj(t)" is

where "M" is the number of samples and

3 Verification

In numerical methods, ensuring the accuracy of the results obtained is very important. For this purpose, a cylindrical structure is dynamic analyzed using MLPG method and the results of this method compare with results of analytical and FEM methods.

3.1 Verification with analytical solution

Figure 2: The geometry and the boundary conditions

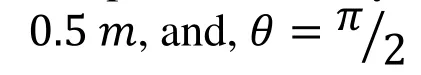
Figs. 3, 4 and 5 show a good agreement in obtained results with this method in comparison of analytical results. Percentage error for radial stress, hoop stress and radial displacement are obtained in Table 1. As can be seen from Table 1, the MLPG method has high accuracy for dynamic analysis of cylindrical structure.

Figure 3: The comparison of obtained results through the MLPG method with those using analytical method for radial displacement

Figure 4: The comparison of obtained results through the MLPG method with those using analytical method for radial stress

Figure 5: The comparison of obtained results through the MLPG method with thoseusing analytical method for hoop stress

Table 1: The comparison of obtained results from MLPG method with those results using analytical method for middle point of thickness of the cylinder

3.2 Verification with FEM

In this section, a FG cylinder using present method under shock loading have been analyzed dynamically. The obtained results compare with FEM [Shakeri, Akhlaghi and Hoseini (2006)]. The boundary conditions are the same as equation (46). The cylinder is under shock loading as follows:

where P0=4 GPa sec⁄. FG material properties are showed in Table 2. Obtained results with MLPG method show a good agreement in comparison of results (Figs. 6, 7 and 8).Percentage difference for radial displacement, radial stress and hoop stress are obtained in Table 3. As can be seen from Table 3, the MLPG method has high accuracy for dynamic analysis of cylindrical structure.

Figure 6: The comparison of obtained results through the MLPG method with those using FEM for radial displacement

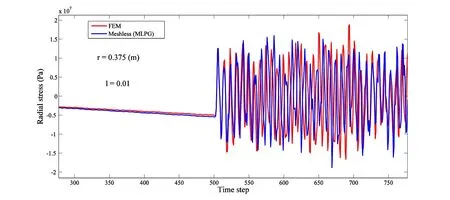
Figure 7: The comparison of obtained results through the MLPG method with those using FEM for radial stress

Figure 8: The comparison of obtained results through the MLPG method with those using FEM for hoop stress

Table 3: The comparison of obtained results from MLPG method with those using finite element method for middle point of thickness of the cylinder at time step 520

4 Numerical results and discussion

To showing capability of the present method for dynamic analysis of the FG cylindrical structure, in the following, we carry out the dynamic analyzed cylinder with different volume fraction exponent using MLPG method under harmonic and rectangular shock loading.

4.1 harmonic shock loading

Figure 9: The geometry and the boundary conditions under shock loading

Figure 10: The time history of radial displacement for l=0.5, l=0.75 and l=1 under harmonic shock loading

Figure 11: The time history of hoop displacement for l=0.5, l=0.75 and l=1 under harmonic shock loading

Figure 12: The time history of hoop stress for l=0.5, l=0.75 and l=1 under harmonic shock loading

Figure 13: The time history of radial stress for l=0.5, l=0.75 and l=1 under harmonic shock loading.

Figure 14: The time history of shear stress for l=0.5, l=0.75 and l=1 underharmonic shock loading.

4.2 Rectangular shock loading

The same geometric and boundary conditions with problem 4.1 are assumed for a nonsymmetric FG cylinder under rectangular shock loading. Table 2 shows material properties for the FG cylinder. The loading is supposed as follow:

where P0=10 MPa is assumed. Radial displacement, hoop displacement, radial stress,hoop stress, and shear stress are illustrated in Figs. 15 to 19. Maximum amplitude of the radial and hoop displacement (Figs. 15 and 16) by increasing the value of volume fraction exponent has decreased, such that, radial displacement increase after the impact loading within the confines of free vibration for l=0.5 suddenly (Fig.15). The peak hoop displacement escalates after the impact loading in the range of free vibration for l=0.5 and l=0.75 and this trend for l=1 is inverse. Fig. 17 shows radial stress, from this figure can conclude that the maximum radial stress occur for l=0.75. In Fig. 18 is seen by increasing the value of volume fraction exponent, the maximum hoop stress rises.Within the confines of free vibration in comparison with forced vibration, the value of hoop stress has a significant growth. The maximum of shear stress occurs in the range of free vibration for l=0.75 (see Fig. 19).

Figure 15: The time history of radial displacement for l=0.5, l=0.75 and l=1 under rectangular shock loading

Figure 16: The time history of hoop displacement for l=0.5, l=0.75 and l=1 under rectangular shock loading

Figure 18: The time history of hoop stress for l=0.5, l=0.75 and l=1 under rectangular shock loading

Figure 19: The time history of shear stress for l=0.5, l=0.75 and l=1 under rectangular shock loading

5 Conclusion

In this paper, dynamic equation of non-symmetric FG cylindrical structure has been exploited using Meshless Local Petrov-Galerkin (MLPG) method. To simulate the mechanical properties of FGM, nonlinear volume fractions have been used in the direction of radius. To obtain the dynamic behaviors of non-symmetric FG cylindrical structure in the time domain, the Meshless Local Petrov-Galerkin (MLPG) method have been combined with Laplace transform method. The major conclusions that have been obtained through the above analysis can be summarized as follows:

• The MLPG method shows that it is a very effective method with high accuracy for dynamic analysis of non-symmetric FG cylindrical structure.

• In comparison to the obtained results of analytical method, the achieved results of MLPG method showed a good agreement, that it demonstrates the MLPG method have high accuracy and capability for dynamic analysis of non-symmetric FG cylindrical structure. The maximum percentage errors in the middle point of thickness of the cylinder for radial displacement, radial stress and hoop stress are 9.89×10−3,0.8872 and 0.5399 respectively.

• For showing the accuracy and capability of the obtained results through the MLPG method for shock loading, these results were compared with the FEM. In this case, the maximum percentage differences between the results of the MLPG method and the FEM at time step 520 and the middle point of thickness of the cylinder for radial displacement, radial stress and hoop stress are 0.011, 1.072 and 0.819 respectively.

• For obtaining the time histories of displacements and stresses for the various values of volume fraction exponent can be used the presented hybrid meshless technique(combined MLPG and Laplace transform method).

• The non-symmetric FG cylindrical structure was analyzed under harmonic shock loading with the various values of volume fraction exponent. This analysis showed,by increasing the value of volume fraction exponent, the radial and hoop displacement maximum amplitude decreased and the similar behaviors can be seen for hoop stress.Also the maximum amplitude of radial stress has not much difference. Clear trend cannot be seen for the shear stress with various values volume fraction exponent.

• The rectangular shock loading applied to the non-symmetric FG cylindrical structure.This analysis showed, the maximum amplitude of the radial and hoop displacement by increasing the value of volume fraction exponent has decreased. The maximum radial stress occur for l=0.75. Also by increasing the value of volume fraction exponent, the maximum hoop stress rises. The maximum of shear stress occurs in the range of free vibration for l=0.75.

• The present analysis furnishes a ground for natural frequency analysis of FGMs with two dimensional grading patterns.

Chen, W. Q.; Bian, Z. G.; Ding,H. J.(2004): Three-dimensional vibration analysis of fluid-filled orthotropic FGM cylindrical shells,International Journal of Mechanical Sciences, vol. 46, pp. 159-171.

Chen, W. Q.; Bian, Z. G.; Ding, H. J.(2004): 3D free vibration analysis of a functionally graded piezoelectric hollow cylinder filled with compressible fluid,International Journal of Solids and Structures, vol. 41, pp. 947-964.

Foroutan, M.; Moradi-Dastjerdi, R.(2011): Dynamic analysis of functionally graded material cylinders under an impact load by a mesh-free method,Acta Mechanica, vol. 219,pp. 281-290.

Hosseini, S. M.; Abolbashari,M. H.(2010): General analytical solution for elastic radial wave propagation and dynamic analysis of functionally graded thick hollow cylinders subjected to impact loading,Acta Mechanica, vol. 212, pp. 1-19.

Hosseini, S. M.; Akhlaghi, M.; Shakeri,M.(2007): Dynamic response and radial wave propagation velocity in thick hollow cylinder made of functionally graded materials,Engineering Computations, vol. 24, pp. 288-303.

Hosseini, S. M.; Shahabian, F.(2011): Stochastic assessment of thermo-elastic wave propagation in functionally graded materials (FGMs) with Gaussian uncertainty in constitutive mechanical properties,Journal Thermal Stresses, vol. 34, pp. 1071-1099.

Hosseini, S. M.; Shahabian,F.(2011): Transient analysis of thermo-elastic waves in thick hollow cylinders using a stochastic hybrid numerical method, considering Gaussian mechanical properties,Applied Mathematical Modelling, vol. 35, pp. 4697-4714.

He, L.; Seaid, M.(2016): A Runge-Kutta-Chebyshev SPH algorithm for elastodynamics,Acta Mechanica, vol. 227, pp. 1813-1835.

Jaberzadeh, E.; Azhari, M.(2015): Local buckling of moderately thick stepped skew viscoelastic composite plates using the element-free Galerkin method,Acta Mechanica,vol. 226, pp. 1011-1025.

Khosravifard, A.; Hematiyan, M. R.; Marin,L.(2011): Nonlinear transient heat conduction analysis of functionally graded materials in the presence of heat sources using an improved meshless radial point interpolation method,Applied Mathematical Modelling,vol. 35, pp. 4157-4174.

Lin, H.; Atluri,S. N.(2000): Meshless local Petrov-Galerkin (MLPG) method for convection-diffusion problems,Computer Modeling in Engineering and Sciences, vol. 1,pp. 45-60.

Liu, G. R.; Gu, Y. T.(2000): Meshless local Petrov-Galerkin (MLPG) method in combination with finite element and boundary element approaches,Computational Mechanics, vol. 26, pp. 536-546.

Moradi-Dastjerdi, R.; Foroutan, M.; Pourasghar, A.(2013): Dynamic analysis of functionally graded nanocomposite cylinders reinforced by carbon nanotube by a meshfree method,Materials and Design, vol. 44, pp. 256-266.

Mirzaei, D.; Hasanpour, K.(2016): Direct meshless local Petrov-Galerkin method for elastodynamic analysis,Acta Mechanica, vol. 227, pp. 619-632.

Najibi, A.; Shojaeefard, M. H.(2016): Elastic mechanical stress analysis in a 2D-FGM thick finite length hollow cylinder with newly developed material model,Acta Mechanica Solida Sinica, vol. 29, pp. 178-191.

Park, K. J.; Kim, Y. W.(2016): Vibration characteristics of fluid-conveying FGM cylindrical shells resting on Pasternak elastic foundation with an oblique edge,Thin-Walled Structures, vol. 106, pp. 407-419.

Rezaei Mojdehi, A.; Darvizeh, A.; Basti, A. et al.(2011): Three dimensional static and dynamic analysis of thick functionally graded plates by the meshless local Petrov–Galerkin (MLPG) method,Engineering Analysis with Boundary Elements, vol. 35, pp.1168-1180.

Shakeri, M.; Akhlaghi, M.; Hoseini, S. M.(2006): Vibration and radial wave propagation velocity in functionally graded thick hollow cylinder,Composite Structures,vol. 76, pp. 174-181.

Shen, H.; Paidoussis, M. P.; Wen, J. et al.(2014): The beam-mode stability of periodic functionally graded material shells conveying fluid,Journal of Sound and Vibration, vol.333, pp. 2735-2749.

Sladek, J.; Sladek, V.; Atluri,S. N.(2004): Meshless local Petrov-Galerkin method in anisotropic elasticity,Computer Modeling in Engineering and Sciences, vol. 6, pp. 477-489.

Sladek, J.; Stanak, P.; Han, Z. et al.(2013): Applications of the MLPG method in engineering and sciences: a review,Computer Modeling in Engineering and Sciences, vol.92, pp. 423-475.

Sladek, J.; Sladek, V.; Stanak, P. et al.(2013): Analysis of the bending of circular piezoelectric plates with functionally graded material properties by a MLPG method,Engineering Structures, vol. 47, pp. 81-89.

Tadeu, A.; Stanak, P.; Antonio, J. et al.(2015): 2.5D elastic wave propagation in nonhomogeneous media coupling the BEM and MLPG methods,Engineering Analysis with Boundary Elements, vol. 53, pp. 86-99.

Ugural, A. C.; Fenster, S. K.(2003):Advanced strength and applied elasticity, Fourth Edition, Prentice Hall.

Xiao, J. R.; Batra, R. C.; Gilhooley, D. F. et al.(2007): Analysis of thick plates by using a higher-order shear and normal deformable plate theory and MLPG method with radial basis functions,Computer Methods in Applied Mechanics and Engineering, vol. 196, pp.979-987.

Zhao, X.; Liu, G. R.; Dai, K. Y. et al.(2008): Geometric nonlinear analysis of plates and cylindrical shells via a linearly conforming radial point interpolation method,Computational Mechanics, vol. 42, pp. 133-144.

Zhang, X.; Song, K. Z.; Lu, M. W. et al.(2000): Meshless methods based on collocation with radial basis functions,Computational Mechanics, vol. 26, pp. 333-343.