Uncertainty Analysis Method of Casing Extrusion Load for Ultra-Deep Wells
2018-01-22MengLiKanhuaSuZijianLiDongjieLiandLifuWan
Meng Li, Kanhua Su, Zijian Li, Dongjie Li and Lifu Wan
1 Introduction
Uncertainty exist in extrusion load on the casing in oil and gas wells is induced by the randomness of formation parameters. The uncertainty of extrusion load on the casing increases in deep wells and ultra-deep wells, where the geology structure is complex and the lithology varies significantly [Long, Li and Guan (2013)]. Numerical value offormation parameters changes in different location, even in different depth of the same formation. Due to the uncertainty of casing extrusion load in ultra-deep well, the risk of casing collapse accident is higher during drilling. According to incomplete survey [Li(2008); Liao, Guan and Feng (2009); Wan, Li and Guan (2012)], casing collapse has occurred in well Dabei 6, well Keshen 2, well Tubei 4, well Keshen 5, well Dabei 203,well Wubo1, well Dongqiu 5, well Chegu 2, well Quele 1, well Xin 101, etc. In reality,the actual value of extrusion load on casing lies in a confidence interval rather than beinga deterministic single value, due to its uncertainty.
Recently, the main stream calculation methods for the prediction of extrusion load on casing are all single deterministic methods [Li and Yin (2006); Pattilo, Last and Asbill(2003); El-Sayed and Khalaf (1992)]. For the first type of the calculation method, it is assumed that the effective extrusion stress is evenly distributed on the outer surface of the casing. Then, the extrusion load is calculated as a uniformly distributed stress. [Pattilo(2003)] calculated the non-uniform extrusion load as equivalent uniform extrusion stress in his model. [Liao (2010)] further developed the equivalent uniform extrusion load model for casing with the consideration of the wear condition of the inner surface of casing. For the second type of the calculation method, based on the uniform distribution load model for casing, the in-situ stress and formation creep are taken into consideration and then the non-uniform load are calculated. [El-Sayed et al. (1989)] presented the calculation model for abnormal damage of casing under the non-uniform extrusion stress.For different casing type and loading feature combination, prediction accuracy for casing damage is calculated correspondingly. [Du et al. (2007)] presented the mechanical model for casing under non-uniform extrusion stress. The distribution of bending moment, shear stress, axial stress, radius stress and displacement on the casing wall are analyzed quantitively. For the third type of calculation model, considering part of the formation parameters, finite element method (FEM) analysis is applied to calculate the non-uniform extrusion stress;then the safety condition of the casing is analyzed. [Shi (2008)]established three-dimension finite element method (FEM) for casing extrusion based on the mudstone creep under non-uniform extrusion stress. [Wan (2012)] carried out finite element method (FEM) analysis on casing extrusion for the extrusion load of different types of casing under different in-situ stresses. However, due to the complexity of the geology structure and the randomness of formation parameters in ultra-deep wells, the prediction methods above for the extrusion load on casing in deep wells and ultra-deep wells are not satisfying.
In order to solve the uncertainty of the extrusion load on the casing in deep wells and ultra-deep wells induced by the randomness of formation parameters and complex geology structure, based on Lame equations, with the consideration of the integrity of formation-cement ring- casing system, an extrusion load prediction model is established for casing in deep wells and ultra-deep wells[Li (2008); Li and Yin (2006)], which is of reference significance to the design of casing and well structure for deep wells and ultra-deep wells.
2 Extrusion load model for casing in ultra-deep wells
2.1 Determination of equivalent density of overlying strata
For wells already drilled, of which the density logging data is available, the equivalent density of overlying strata can be calculated using the discrete integral formula [Fan, Ye and Ji (2011)]:

For the wells undrilled, the calculation of the equivalent density of overlying strata should be carried out based on the density logging data of adjacent wells.
For the well interval near surface with no available density logging data, the equivalent density of overlying strata can be obtained from the continuous fitting function:

Where,his the depth, m.A,B,C,Dare fitting coefficients, dimensionless.

Figure 1: Equivalent density profile of overburden pressure for GN-203 well
2.2 Establishment of extrusion load for casing in ultra-deep wells
Because of the complexity of the geology structure and randomness of formation parameters for ultra-deep wells, an error exists in the convention extrusion load calculation model the result. In addition, the unloading effect of well cured cement ring to the casing also influence the accuracy of the calculation result [Wang, Li and Yang(2008); Klever and Tamano (2004); Yang and Chen (2006); Aasen, Bernt and Aadnoy(2007)]. Thus, based on Lame equations and equivalent non-uniform extrusion stress model for formation-casing system, with the consideration of the integrity of formation-cement ring-casing system, the extrusion load prediction model is established for casing in ultra-deep wells.


3 Uncertainty analysis of extrusion load on casing in ultra-deep wells
3.1 Analysis of parameters′ randomness of extrusion load on casing in ultra-deep wells
(1) Comparison of coefficient of variation for extrusion load.
(2) Determination of the distribution types of formation elastic modulus and formation Poisson’s ratio.
Formation elastic modulus and formation Poisson’s ratio of each formation are analyzed statically as shown in the histograms in Fig 3 and Fig 4. Non-linear fitting is conducted using equation (10) to (12) [Sun and Chen (2003)]. The fitting result is shown in the fitting curve in Fig 3 and Fig 4.
Normal distribution:
The randomness of parameters can be evaluated by coefficient of variation, which is defined as:

Where,COVis the coefficient of variation for a random variable, dimensionless;is the standard deviation of the random variant;is the mean value of the random variant.According to the statistical result of 2000 different steel grade casings from 5 manufacturers [Adams, Parfitts and Reeves (1993)] and addition research [Prasongsit,Paolo and Jerome (2001)], case study is carried out using the ultra-deep well data in Shanqian block of Western Oilfield of China. The COVs of influence parameters of extrusion load on casing are obtained statistically as shown in Fig 2. According to the result, it is noted that the COV of formation elastic modulus and formation Poisson’s ratio is much larger than the COV of casing elastic modulus, casing Poisson’ ratio,drilling fluid density, casing size or any other parameters. It is concluded that the randomness of formation elastic modulus and formation Poisson’s ratio are the main influence factors on the uncertainty of extrusion load on casing.
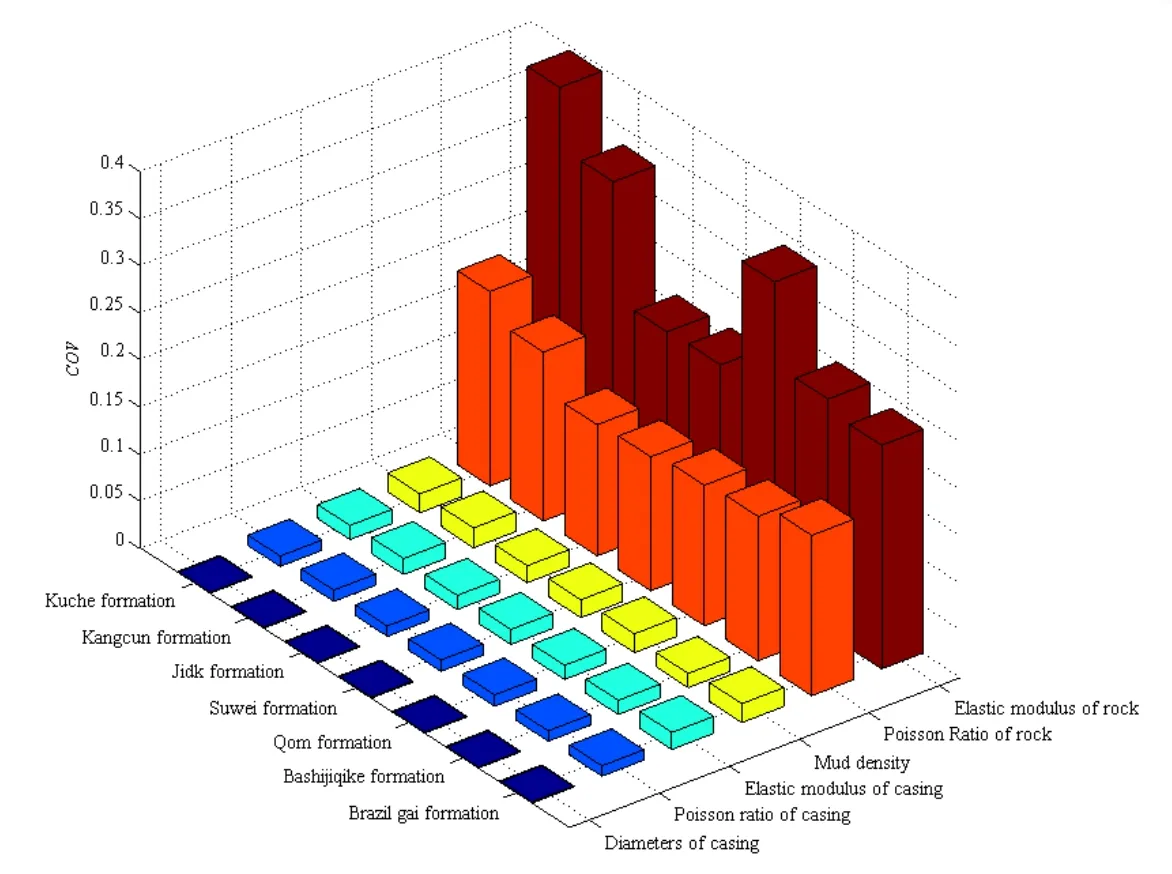
Figure 2: Comparison of variation coefficients of main parameters of extrusion load in ultra deep wells

Lognormal distribution:



Figure 3: Elastic modulus statistics and fitting distribution results in each layer

Figure 4: Statistics and fitting distribution results of Poisson's ratio in each layer
Correlation tests between statistic results and fitting curves are carried out [Xiao (2002)],then the average correlation coefficients of formation elastic modulus and formation Poisson’s ratio with respect to these three distribution types mentioned above are obtained. The result is shown in table 1.

Table 1: Average correlation coefficient
It is noted that the average correlation coefficients of normal distribution of formation elastic modulus and formation Poisson’s ratio are 0.962 and 0.921 respectively, which shows that significant strong correlations exist between statistic results and normal distribution. In addition, the average correlation coefficients of normal distribution are obviously larger than those of lognormal distribution and Weibull distribution, as shown in table 1. Thus, normal distribution is the best distribution type for the statistic result of formation elastic modulus and formation Poisson’s ratio.
3.2 Determination of the distribution type of extrusion load on the casing in ultra-deep wells
Formation elastic modulus and formation Poisson’s ratio, which are the main influence factors of extrusion load on the casing, are regarded as two-dimensional variables.Suppose that the extrusion loadpis expressed byZ, formation elastic modulus is expressed byXand formation Poisson’s ratiois expressed byY. Then, their random values are represented asz, xandy. Then, equation (8) can be transformed to:




According to probability theory [Xiao (2002)], the probability density function ofzcan be expressed as:

Given that formation elastic modulusand formation Poisson’s ratioobey normal distribution, distribution ofcan be expressed using equation (10).


Make the integration of equation (18), the cumulative probability function of extrusion load on casing in ultra-deep wells can be obtained:

Known from equation (18) that the uncertainty of extrusion load on casing in ultra-deep wells obeys normal distribution. For a given cumulative probability, the correlating extrusion load can be calculated using equation (19). Taking GN-101 well in Shanqian block as an example, probability density and cumulative probability of extrusion load are calculated and plotted in Fig 5.

Figure 5: Equivalent density distribution of external collapse load
3.3 Analysis on the confidence interval of extrusion load on casing in ultra-deep wells





4 Case study
Taking Shanqian block in Western oilfield, China as an example, the uncertainty of extrusion load on casing in ultra-deep wells are analyzed. The data is selected from three wells. In this block, the stratigraphic sequence from the surface downward is Kuqa formation, Kangcun formation, Jidk formation, Suwei formation, Qom formation,Bashijiqike formation and Brazil gai formation. Firstly, equivalent density profile of overlying strata is constructed. Then, formation elasticity modulus and formation Poisson’s ratio are analyzed statically and the distribution types and distribution parameters’ characterization values are obtained, as shown in table 2. Using equation(19), which is the cumulative probability function of extrusion load on casing, the equivalent density of extrusion load is calculated along the wellbore downward with respect to the cumulative probability of 5%, 95%, 35 and 65%. The distribution intervals of equivalent density of extrusion load corresponding to the confidence levels of 90% and 30% are obtained respectively. The results are compared with the result of traditional calculation method.
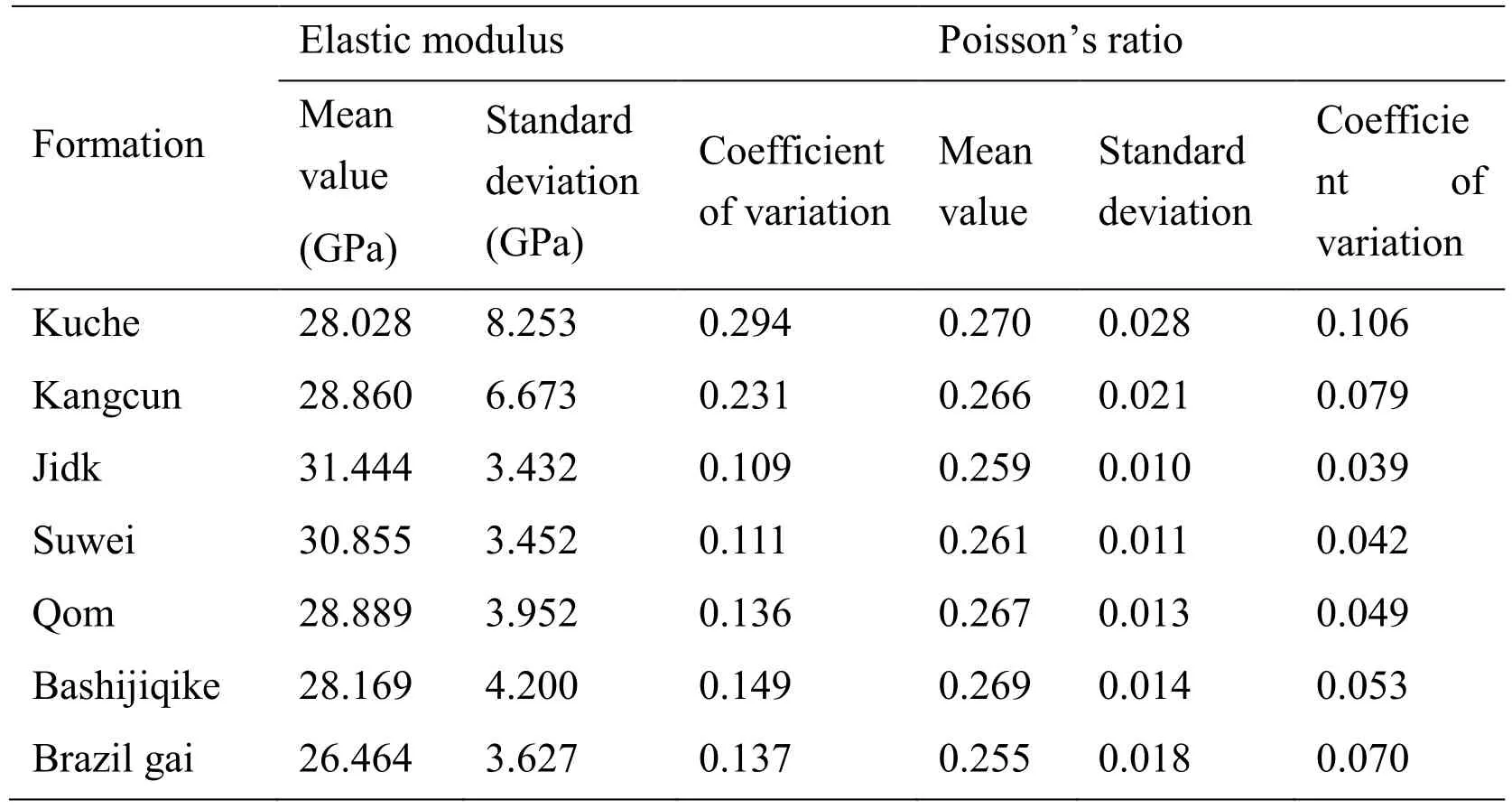
Table 2: Statistical results of randomness of main formation parameters in different formations in Shanqian block
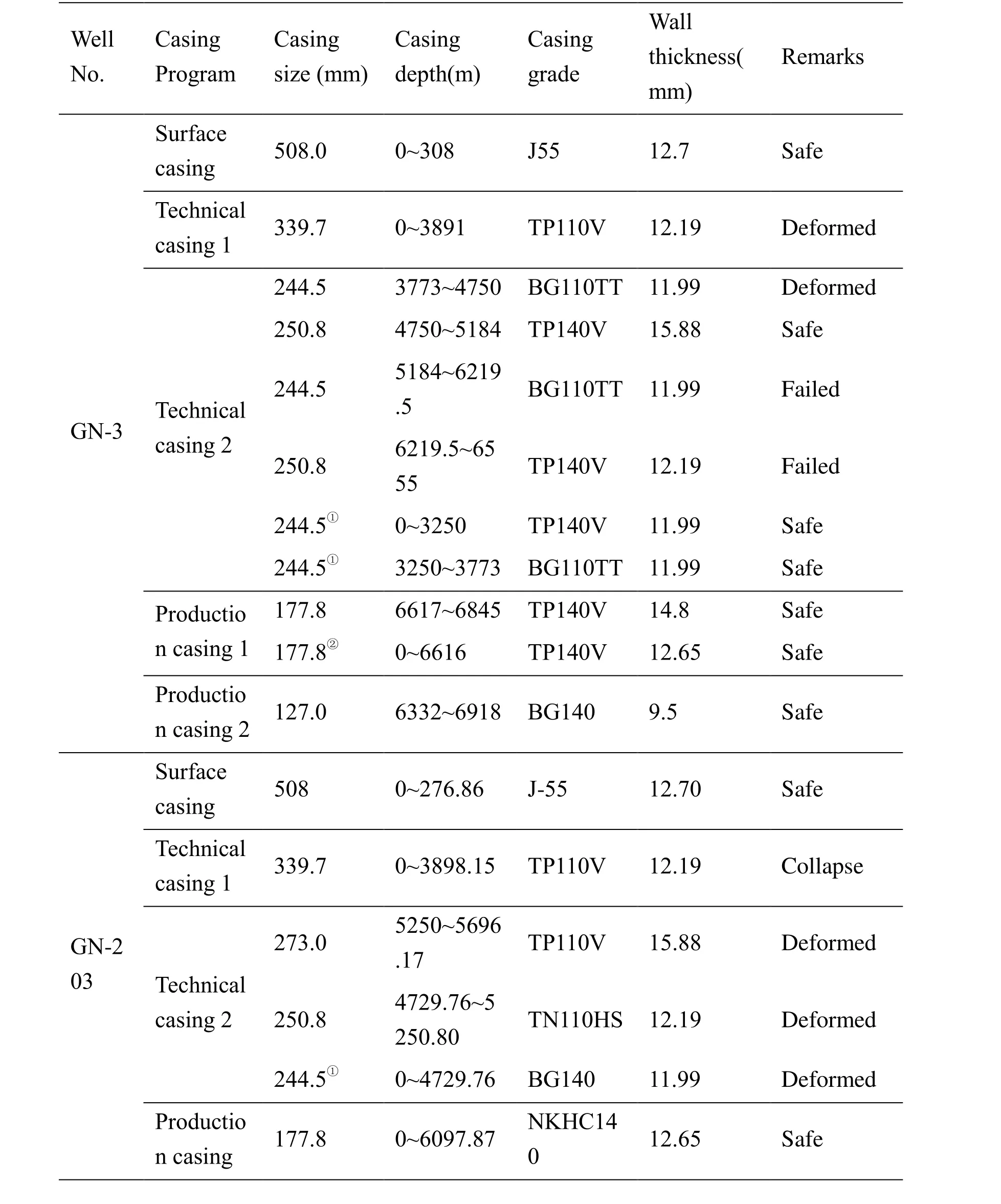
Table 3: Casing program and safety situation in GN-3 well
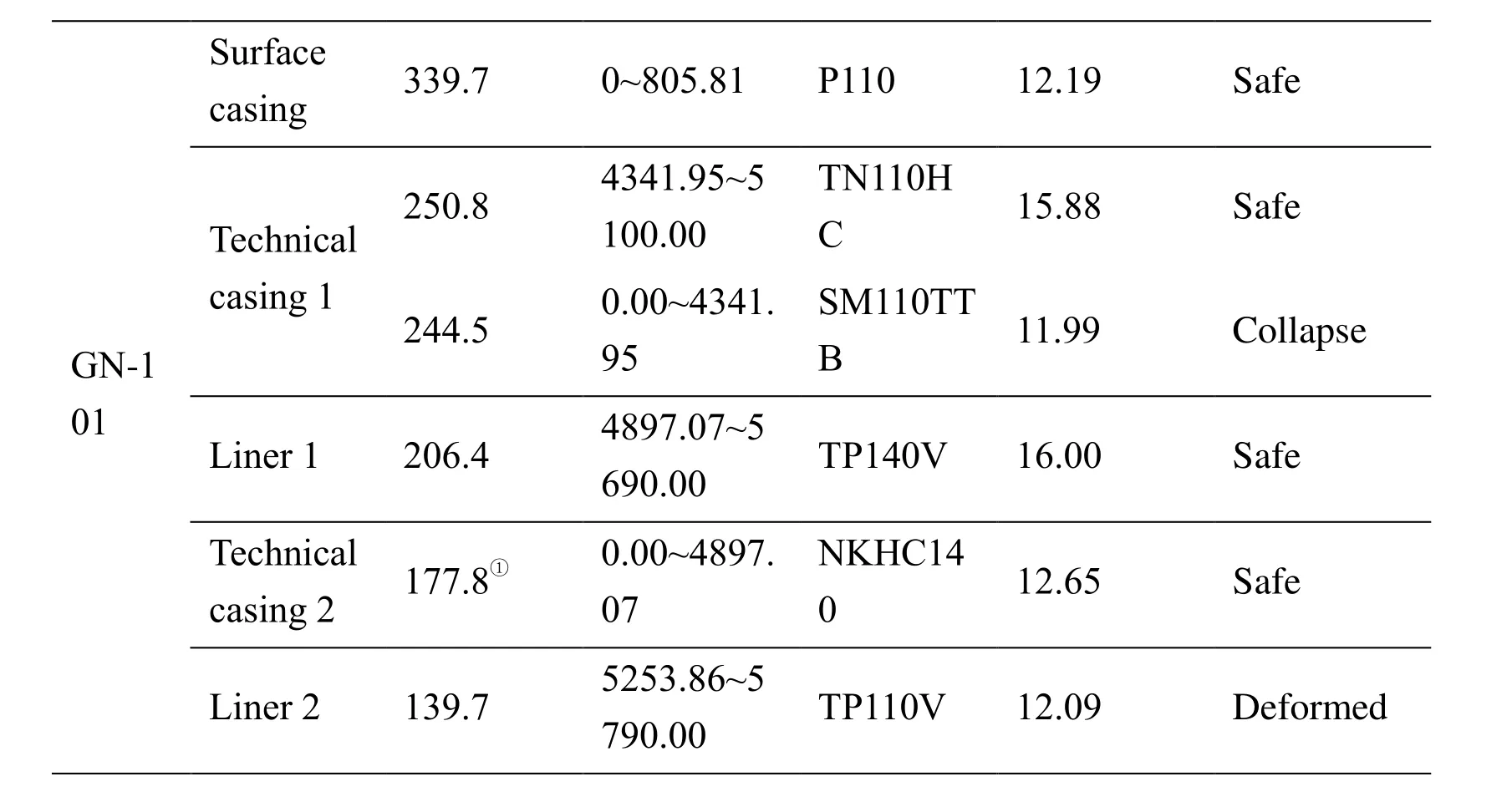
Note: Technical casing 1 is the first layer of technical casing, Technical casing 2 is the second layer of technical casing, Production casing 1is the first layer of production casing, Production casing 2 is the second layer of production casing, ① or ② is tie back casing.

Figure 6: Equivalent density profile of casing extrusion load with different confidence levels
Note: (I) is the distribution of the extrusion load interval with a confidence level of 90%,(II) is the distribution of the extrusion load interval with a confidence level of 30%
According to the statistical probability results of formation elasticity modulus and formation Poisson’s ratio in table 2, for three wells of GN-3, GN-203 and GN101, the casing extrusion load confidence intervals correlating to the confidence levels of 90% and 30% are obtained by using equation (18), (19) and (20), as shown in Fig. 6. Unlike the traditional method result of casing extrusion load, which is a single curve, for which the extrusion load on the casing for a certain depth is a deterministic value, the extrusion load on the casing for a certain depth obtained by new uncertainty analysis varies in a range. It is because that the variation of formation parameters of each formation along the ultra-deep well is considered in the calculation of casing extrusion load confidence interval with a certain confidence level. For practical design of drilling engineers, the variation range of casing extrusion load is of more significance than a single deterministic value obtained by using the traditional method. If the single deterministic casing extrusion load value is higher than the actual variation range of casing extrusion load, higher grade of casing will be selected. The over-engineering will induce an increase in cost. Otherwise, if the single deterministic casing extrusion load value is lower than the actual variation range of casing extrusion load, lower grade of casing will be selected. The under-engineering will increase the risk of casing collapse. Thus, the casing extrusion load variation range obtained by using the new method is of more significance in the design, by decreasing the accident risk and the cost in casing.
It is seen from Fig. 6 (a)(I) that in the well section from depth 1200m to 2800m, the deterministic value of casing extrusion load obtained using the traditional single valued method appears to be a little higher than or close to the equivalent density corresponding to the cumulative probability of 95%. Known from Fig. 6 (a)(II) that in the well section from depth 1200m to 2800m, the deterministic value of casing extrusion load obtained using the tradition single valued method is higher by 0.17g/cm3on average than the equivalent density corresponding to the cumulative probability of 65%. This suggests that the steel grade of the casing is higher than enough and an over-engineering and a waste of cost exist. In the well section from depth 5200m to 7000m, the deterministic value of casing extrusion load obtained using the traditional single valued method is lower by 0.12g/cm3and 0.18g/cm3on average than the equivalent density corresponding to the cumulative probability of 5% and 35% respectively. This suggests that the steel grade of the casing is lower than enough and an under-engineering and an increase in risk of casing collapse exist.
Known from Fig. 6 (b) that in the well section from depth 0m to 1500m, the deterministic value of casing extrusion load obtained using the traditional single valued method is higher by 0.1g/cm3- 0.2g/cm3and 0.1g/cm3- 0.4g/cm3than the equivalent density corresponding to the cumulative probability of 95% and 65% respectively. This suggests that the steel grade of the casing is higher than enough and an over-engineering and a waste of cost exist. In the well sections from depth 3100m to 3600m and from depth 4000m to 6000m, the deterministic value of casing extrusion load obtained using the tradition single valued method is lower by 0.12g/cm3and 0.2g/cm3on average than the equivalent density corresponding to the cumulative probability of 5% and 35%. This suggests that the steel grade of the casing is lower than enough and an under-engineering and an increase in risk of casing collapse exist.
Known from Fig. 6 (c) that in the well section from depth 0m to 2800m, the deterministic value of casing extrusion load obtained using the traditional single valued method lies in the equivalent density ranges corresponding to the cumulative probability of [5%, 95%]and [35% ,65%]. This suggests that the steel grade of the casing is selected reasonably. In the well sections from depth 3000m to 3500m and from depth 5200m to 6200m, the deterministic value of casing extrusion load obtained using the tradition single valued method is lower by 0.1g/cm3- 0.12g/cm3and 0.1g/cm3- 0.2g/cm3than the equivalent density corresponding to the cumulative probability of 5% and 35%. This suggests that the steel grade of the casing is lower than enough and an under-engineering and an increase in risk of casing collapse exist.
Comparing Fig. 6 (I) and Figure 6 (II), it is noted that at a certain well depth, the higher the confidence level is, the larger the confidence interval and the window of casing extrusion load equivalent density are. Otherwise, at a certain well depth, the lower the confidence level is, the smaller the confidence interval and the window of casing extrusion load equivalent density are. However, if the confidence interval is too large, the selected casing steel grade will be too high, increasing the cost. In this situation, the confidence interval can be evaluated and adjusted to be smaller according to the practical geology condition of adjacent wells which are already drilled. In addition, referring to the field drilling experience of other wells in this block, formation parameters can be corrected by omitting the highly deviated data. Then, the random distribution range of formation parameters will be narrowed. Thus, a smaller distribution range of the extrusion load on casing is obtained at a relatively high confidence level. However, even at the same confidence level, the window of equivalent density of extrusion load on casing varies with the well depth. It is because that the randomness level of formation parameters is different at different depth.
Applying the same method, the equivalent density of extrusion load on casing is calculated for more than 30 wells in this block, where casing collapse accidents happened. The extrusion loads of each program of casing obtained using the traditional method is checked whether they lie in the 90% confidence interval obtained by the new uncertainty analysis method. Then the ratio of the number of wells of which the traditional result lies in the interval at the confidence level of 90% obtained by the new method to the total well number is calculated, as shown in Figure 7. The safety factors obtained using the traditional method are compared with those obtained using the new uncertainty analysis. The result is shown in Figure 8. The number of failure predicted using the traditional method and the number of failure predicted using the new uncertainty analysis are obtained and their ratio is also calculated, as shown in Figure 9.

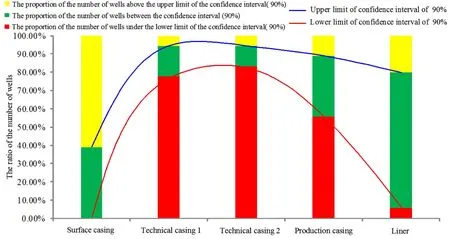
Figure 7: The proportion of the number of well at which the extrusion loads on casing obtained using the traditional method lie in and outside of the confidence interval at the confidence level of 90% obtained by the new uncertainty analysis method


Figure 8: Comparison of casing collapse safety factor
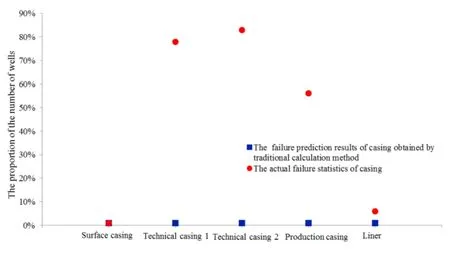
Figure 9: Proportion of casing failure wells for each casing program

Based on uncertainty analysis method, it is concluded thatvalue is always larger than required, which induces an over-engineering and an increase in cost. It is proved by the well history that no surface casing collapse accident took place, as shown in Figure 9.
Regarding to technical casing 1, technical casing 2 and production casing, as shown in Figure 7, in portions of 77.8%, 83.3% and 55.6% of all the wells,≤; while<<in portions of 16.7%, 11.1% and 33.3% of all the wells and≥only in portions of 5.6%, 5.6% and 11.1% of all the wells. To sum up, the extrusion load on these 3 types of casing calculated using the traditional method is always lower than that calculated using the new uncertainty analysis method. The calculation result of,andshows thatis always lower thanand, as shown in Figure 8 (b), Figure8 (c) and Figure 8 (d). Based on the uncertainty analysis method, it is concluded that is always lower than the value required, inducing an under-engineering and an increase in risk of casing accident for technical casing 1,technical casing 2 and production casing. Using traditional method, the predicted casing collapse accident number is zero. However, according to the well history, that the portions of wells where casing collapse accidents took place in technical casing 1,technical casing 2 and production casing are 80%, 82.8% and 56% respectively, as shown in Figure 9. Thus, a better accuracy of uncertainty analysis method than the traditional method is proved.
Regarding to the liner, as shown in Figure 7, in a portion of 74.4% wells,<<;in a portion of 20% wells,≥;while only in a portion of 5.6% wells,≤. In other words, the extrusion load on liner calculated using traditional method always lies in the 90% confidence interval obtainedusing uncertainty analysis. Accordingto equation (22) to (24), for most of the wells, lies in the range of [,], as shown in Figure 8 (e), suggesting that the design of liners are safe for most wells. The number of liner collapse accidents is predicted to be zero using tradition method, and only three collapse accident took place on liner according to the well history, as shown in Figure 9. Thus, a better accuracy of new uncertainty analysis method than the traditional method is proved.
In summary, based on traditional calculation method for casing extrusion load, the design of surface casing is over-engineered, while the design of technical casing and production casing is under-engineered, of which the safety is questionable. For the design based on new uncertainty analysis method, surface casing of lower steel grade is favorable, which decreases the casing cost; however, higher steel grade will be selected for technical casing and production casing to ensure the safety against collapse. Compared with the traditional casing extrusion load calculation method, of which the result of extrusion load of a certain depth is a deterministic single value, the variation of extrusion load with depth is taken into consideration in new uncertainty analysis method. For deep wells and ultra-deep wells, new uncertainty analysis method better describes the real load condition of the casing. The variation range of extrusion load on casing obtained using new uncertainty analysis method is more reliable as a reference for the determination of the casing safety factor against extrusion than the single valued result of traditional method.Then, by the application of a better safety factor value, waste of over-engineering is avoided and the safety of casing is better ensured.
5 Conclusion
(1) With consideration of the randomness of formation parameters, which influences the uncertainty of the extrusion load on the casing in ultra-deep wells, a new uncertainty analysis method is presented for the extrusion in ultra-deep wells.
(2) Because of the uncertainty of the extrusion load on casing in complex geology structure, the value of the extrusion load at a certain depth should be described as a confidence interval at a certain confidence level, rather than a single curve. The description of confidence interval is of more significance in the characterization of the in-situ stress condition in complex geology structure.
(3) As the increase of the confidence level, the reliability of the extrusion load on casing in ultra-deep wells increases, while the range of uncertainty increases as well. Otherwise,reliability and range of uncertainty decrease with the confidence level. Thus, it is recommended that the collection of precise geology information is of great significance because it is the proof for the correction of formation data by omitting the highly deviated data. Then, the uncertainty range of the extrusion load on casing will be decreased. The increase in the accuracy of determination of the extrusion load on casing is advantageous to a more reasonable design of well structure, the guarantee of safety and decrease of cost.
(4) According to the analysis on several wells in Shanqian block, it is concluded that the new uncertainty analysis provides a more reasonable prediction result of extrusion load on casing in ultra-deep wells than traditional single valued method. It is proved that the new uncertainty analysis method is more reliable as a reference for the design of well structure and the selection of casing in deep wells and ultra-deep wells.
Acknowledgements:This work was supported by the National Science and Technology Special Project of China[2016ZX05022-002], the Chongqing Research Program of Basic Research and Frontier Technology [CSTC2015jcyjA90021], and the Scientific and Technological Research Program of Chongqing Municipal Education Commission[KJ1501302], and the Academician Led Special Project of Chongqing Science and Technology Commission [CSTC2017zdcy-yszxX0009]. This research is also supported by other projects (Grant numbers: 2017ZX05009003-007, 2016D-5007-0308, 51374266,51774063).
Aasen, J. A.; Bernt, S.; Aadnoy.(2007): Three-dimensional well tubular design improves margins in critical wells.Journal of Petroleum Science and Engineering, vol. 56, no. 4, pp.232-240.
Adams, A. J.; Parfitts, H. L.; Reeves, T. B. et al.(1993):Casing system risk analysis using structural reliability,SPE/ IADC25693.
El-Sayed, A. H.; Khalaf, F.(1992): Resistance of cemented concentric casing strings under non-uniform loading.SPE Drilling Engineering, vol. 7, no. 1, pp. 59-64.
Fan, H. H.; Ye, Zhi.; Ji, R. Y.(2011): Investigation on three-dimensional overburden pressure calculation method. ChineseJournal of Rock Mechanics and Engineering, vol.30, no. 2, pp. 3879-3883.
Klever, F. J.; Tamano, T.(2004):A new OCTG strength equation for collapse undercombined loads. SPE 90904.
Liao, H. L.; Guan, Z. C.; Feng, G. T.(2009): Casing failure mechanism and strength design considerations for deep and ultra-deep wells.Oil Drilling & Production Technology, vol. 31, no. 2, pp. 1-4.
Long, G.; Li M.; Guan, Z. C.(2013): Evaluation method of casing safety and reliability in deep wells.Petroleum Drilling Techniques, vol. 41, no. 4, pp. 48-53.
LI, M.(2008):Analysis on Distribution of Load Uncertainty and Safety and Reliability of Casing in Ultra-deep Well. Qingdao: China University of Petroleum (East China).
Li, Z. M.; Yin, Y. Q.(2006):Casing external loading calculation and its mechanics foundation in oil wells. Beijing, Petroleum Industry Press.
Pattilo, P. D.; Last, N. C.; Asbill, W. T.(2003):Effect of nonuniform loading on conventional casing collapse resistance. SPE 79871.
Prasongsit, C.; Paolo, G.; Jerome, S.(2001):Structural reliability: assessing the condition and reliability of casing in compacting reservoirs. IPTC 14297.
Steve, H.(1999):Pre-drill overburden estimation. [S.l.]: [s.n.].
Sun, Z.; Chen, L.(2003):Practical mechanical reliability design theory and method.Beijing: Science Press.
Wan, L. F.; Li, G. S.; Guan, Z. C.(2012): A numerical analysis of the actual external collapse load on deep-well casing in its strength design. ChinaPetroleum Machinery,vol.40, no. 4, pp. 1-4.
Wang, Y. F.; Li, J. Q.; Yang, X. H.(2008): Stress Distribution in Casing-Cement-Stratum.Petroleum Drilling Techniques, vol. 36, no. 5, pp. 8-12.
Xiao, X. N.(2002):Probability theory and mathematical statistics. Beijing: Peking University.
Yang, H. L.; Chen, M.; Jin, Y.(2006): Analysis of casing equivalent collapse resistance in creep formations.Journal of China University of Petroleum, vol. 30, no. 4, pp. 95-98.
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- Simulation of Dynamic 3D Crack Propagation within the Material Point Method
- The Stable Explicit Time Stepping Analysis with a New Enrichment Scheme by XFEM
- Numerical Simulation of Coal Deformation and Gas Flow Properties Around Borehole
- Soil Microbial Dynamics Modeling in Fluctuating Ecological Situations by Using Subtractive Clustering and Fuzzy Rule-Based Inference Systems
- Modeling and Analysis of Novel Multilevel Inverter Topology with Minimum Number of Switching Components
- Dynamic Analysis of Non-Symmetric Functionally Graded (FG)Cylindrical Structure under Shock Loading by Radial Shape Function Using Meshless Local Petrov-Galerkin (MLPG) Method with Nonlinear Grading Patterns
