Garmin手持式GPS的坐标转换方法研究

2018-01-22刘生荣

西部探矿工程 2018年1期

杜辉，刘生荣，高鹏

（中国地质调查局西安地质调查中心，陕西西安 710054）

1 概述

随着全球卫星定位系统（GPS）技术的广泛普及，手持GPS在森林普查、土地调查、电力勘测、地质调查等各行各业的应用也非常普遍。Garmin手持式GPS是美国Garmin公司推出的系列功能强大的手持机型，具有搜星速度快、操作简单、单点定位精度高等优点，且配套的MapSource软件能够方便地进行数据传输、坐标系转换[1]，这些优点使其成为一种必不可少的野外作业工具。

2 常见的坐标转换方法

由于Garmin手持GPS采用WGS-84坐标系，椭球基准为WGS-84，这与我国常用北京54和西安80坐标系的椭球质心和椭球参数不同，北京54坐标系采用的椭球为克拉索夫斯基1940，西安80坐标系采用的椭球为IAG75椭球，相应的椭球参数见表1。因此需要设置参数，将WGS-84坐标转换为实际所用的坐标后才能满足我们工作的要求[2]。

Garmin手持GPS中需要设置的参数与MapSource软件中的完全一致，均为Delta X、Delta Y、Delta Z、Delta半长轴、Delta平面度（图1），一般表示为ΔX、ΔY、ΔZ、ΔA、ΔF。ΔX、ΔY、ΔZ称为坐标轴平移三参数，ΔA、ΔF为椭球基准转换参数。

如何计算这些参数，是正确进行坐标转换的关键。实际生产中，通常是利用具有2套坐标系下坐标的公共点数据进行计算，常见的手持式GPS坐标转换参数的计算方法有：

（1）空间直角坐标过渡法：该方法利用空间直角坐标的计算公式[式（1）]，计算不同坐标系三维空间直角坐标值，然后利用WGS-84坐标系的X、Y、Z值，减去我国坐标系的对应值，得出实现坐标系转换的ΔX、ΔY、ΔZ，转换目标椭球确定后，ΔA和ΔF可利用表1中的相关参数求差计算得出[3-6]。

表1 不同坐标系对应的椭球参数

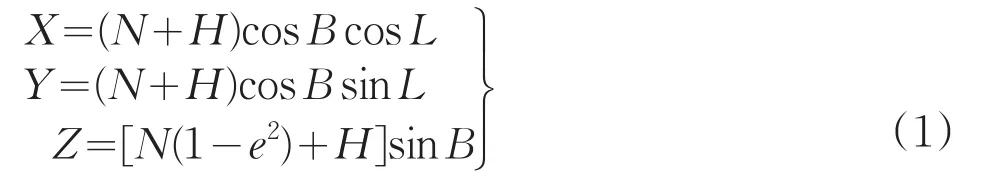
（2）高斯坐标直接加减法：一般情况下，已知的WGS-84坐标为大地坐标系（B、L、H），我国坐标系为高斯坐标（x、y、h），该方法利用高斯正算公式，将大地坐标系换算为高斯投影坐标系，然后利用利用WGS-84坐标系的x、y、h值，减去我国坐标系的对应值，得出实现坐标系转换的ΔX、ΔY、ΔZ，ΔA和ΔF的求法与方法（1）的相同。

图1 MapSource参数设置窗口

（3）参数拟合法：该方法是先将坐标轴平移参数全部设为0，椭球基准转换参数的求法与方法（1）的相同。然后利用手持机在一个控制点上进行实地观测，根据参数变化的规律，采用趋近法求出各自参数[7-8]，将该参数设置好后，再到其他控制点上进行检核，当坐标误差值满足一定限差（一般≤10m）要求时，即可认为该参数符合要求。参数的变化规律为：

当ΔY、ΔZ不变时，ΔX变大，x坐标值变小，y坐标值变大，ΔX主要影响y坐标值。

当ΔX、ΔZ不变时，ΔY变大，x坐标值变大，y坐标值变大，ΔY主要影响x坐标值。

当ΔX、ΔY不变时，ΔZ变大，x坐标值变小，y坐标值不变，ΔZ只影响x坐标值。

3 坐标转换方法研究

3.1 常见参数计算方法的适用性分析

对上述3类常见的转换方法进行研究，发现以下几个问题：

（1）Garmin手持式GPS和Mapsource软件自带的坐标系统中不包括空间直角坐标系，那么通过空间直角坐标系过渡的方法是否能够准确求的Garmin手持GPS的坐标转换参数。

（2）高斯坐标为投影平面直角坐标系，其坐标值与投影时采用的中央经度有关，坐标变化率只反映投影中央经线的不同，不能反映立体的椭球之间由于质心不一致所引起的坐标轴平移变化，理论上表明该方法不适合求取Garmin手持GPS的坐标转换参数。

（3）在实际工作中进行参数拟合时，如果公共点较多，那么所要实地观测的工作量较大，且拟合精度的优劣完全取决于个人的经验。

由于MapSource中坐标转换的方法与Garmin手持机中的完全一致，下面利用MapSource软件举例分析空间直角坐标过渡法、高斯坐标直接加减法在Garmin手持机坐标转换参数计算中的适用情况。

如图2，MapSource V6.16.3版本设置转换参数的位置是：单击菜单栏的“编辑”，在下拉菜单中点击“首选项”命令，弹出首选项对话框。单击“位置”标签，可以对下列选项进行设置:网格—从下拉列表框中可选择“纬度/经度hddd°mm'ss．s″”(度、分、秒格式)或用户定义的网格的网格（高斯投影格式）；基准—从下拉列表框中可选择“WGS-84”(Garmin Corp，2004)或用户定义的基准（坐标转换参数输入）。

假设有3个同时具有WGS-84坐标和北京54坐标的公共点，各坐标系统的坐标值见表2。

根据空间直角坐标系过渡法和高斯坐标直接加减法，计算得出坐标轴平移三参数见表3。

转换目标椭球为克拉索夫斯基1940，椭球基准转换参数即为已知值。将上述平均3参数及ΔA、ΔF输入用户定义的基准属性窗口的对应位置，用户定义的网格属性窗口中输入中央经线、比例系数和东偏移等高斯投影参数，确定后，即可得出上述公共点的x、y、h坐标值。由于MapSource坐标转换时，高程保持不变，现将转换得出的x、y坐标值与实际坐标值进行比较，差值见表4。

由表4可以看出，转换的坐标值与实际值差别较大，证明空间直角坐标过渡法和高斯坐标直接加减法不适用于Garmin手持式GPS的坐标转换参数计算。

3.2 广义大地坐标微分公式计算转换参数研究

考虑到MapSource软件不能定义空间直角坐标系，根据广义大地坐标微分公式，将式（1）取全微分[9]：

其中J和C均为系数矩阵，略去旋转参数项和尺度变化项，并整理得：

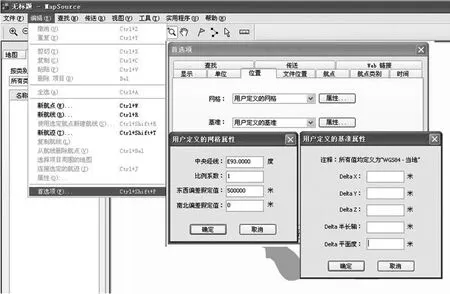
图2 MapSource软件设置参数的位置

表2 公共点各坐标系统的坐标值

表3 两种方法计算的三参数

表4 两种方法转换的坐标值与实际值较差表

以从WGS-84坐标系向北京54坐标系转换为例，（3）式右侧矩阵中的大地纬度B、大地经度L、大地高H、子午圈曲率半径M、卯酉圈曲率半径N、第一偏心率平方e2、长半轴A、扁率F均为WGS-84坐标及其对应的椭球参数；ΔA和ΔF为WGS-84对应椭球和北京54坐标对应椭球（克拉索夫斯基1940）的长轴差和扁率差。

（4）式中的B1、L1、H1为公共点的WGS-84大地坐标，B2、L2、H2为北京54大地坐标，北京54大地坐标的B和L可以根据高斯反算公式计算得出，考虑到GPS测高精度低，MapSource转换时，保持高程不变的特点，北京54坐标的大地高H可以利用该点的正常高h代替。

上述坐标转换方法称为大地坐标微分法。根据3个公共点的2套大地坐标值，可以列出9个（3）式的方程，采用矩阵运算即可求的其中的3个平移参数ΔX、ΔY、ΔZ，同时也解决了有多余观测时参数求解的问题。如果有多余观测（3个以上的公共点）时，可以利用间接平差原理组成误差方程，根据最小二乘原理即可求的方程的最优解。

采用表2中公共点的坐标数据，根据大地微分公式法求取平移三参数，利用与验证空间直角坐标系过渡法和高斯坐标直接加减法相同的方式进行转换计算，转换得出的x、y坐标值与实际坐标值差值见表5。