光纤延迟线实时高精度延迟时间测量方法
2018-01-22王克让姜宇航朱晓丹
张 鑫,王克让,陈 卓,姜宇航,朱晓丹
(1.中国航天科工集团8511研究所,江苏 南京 210007; 2.西安电子科技大学通信工程学院,陕西 西安 710126)
0 引言
作为微波光子技术的一个重要应用,光纤延迟线相比传统的电延迟具有体积小、质量轻、带宽宽、损耗低、抗干扰能力强等优点[1],逐渐应用到雷达系统及电子对抗系统等领域[2],比如光纤延迟线在传统相位干涉仪中的应用,利用光纤延迟线将不同天线接收到的信号进行延迟,使系统能够分时处理各路信号,可以有效解决传统相位干涉仪设备量大、系统复杂的问题,这也是现在相位干涉仪研究领域的热点问题。
为了能够提取信号完整信息,延迟保存的时间需要达到微秒级,导致光纤的长度较长,同时光纤延迟线的延迟时间受到环境尤其是温度的影响会发生改变。对于1000m的光纤,温度变化1℃延迟时间变化约27ps,对于频率为1GHz的信号提取相位差变化约为9.72°,而实际中温度变化远不止1℃,信号频率也大于1GHz,导致产生非常大甚至超过一个周期的额外鉴相误差。这类误差会随着温度的改变而改变,且无法通过校正通道幅相误差将其去除,因此需要实时高精度测量光纤延迟线延迟时间的方法得到此时延迟线的精确延迟时间,从而校正此类误差,为了不影响传统干涉仪对鉴相误差低于30°的要求,需要测量延迟时间精度达到皮秒级,该测量方法对于光纤延迟线应用到更多电子系统中具有参考价值。
测量光纤延迟线延迟时间的方法主要有光学测试法和射频信号测试法,光学测试法主要有光时域后向反射法[3]和光学干涉法[4],该类方法需要精密的光学设备,用于实时测量延迟时间时难以集成到电子设备中。射频信号测试法主要有时域法[5]和频域法[6],时域法又叫做时间数字转换法,该方法以TDC-GPX芯片为核心,通过TDC-GPX时间数字转换器芯片门电路延迟单元与高速探测器匹配进行时间测量,因此需要增加电路模块,提高了系统复杂度和成本;频域法是目前常用的实时测量延迟时间的方法,其主要原理是通过测量输入输出信号之间的相位差,利用多组频率-相位差关系得到相频曲线,由于是统一的延迟时间,该曲线近似一条直线,可利用该直线斜率求得延迟时间[7]。该方法测量方便,精度较高,需要通过增加信号处理带宽或测量频率点数来提高测量精度,这就需要增加校正信号带宽或者时间上的积累,都会增加实际应用的难度。
频域法通过对一个频段内的信号求相位差与信号频率的关系得到该频段的群延迟,每个频点的相位差都存在2π模糊问题,实际中可以通过解得单频点的无模糊相位差得到延迟时间,同时单频点信号频率相当于只利用一个频点信息达到了扩展处理带宽的目的,可以大大降低算法复杂度和系统处理时间。基于以上思想本文提出了基于线性拟合的高精度实时测量方法,通过解单频点信号的相位差模糊数得到无模糊相位差,得到精确延迟时间,该方法无需宽带校正信号源,从而获得更高精度的测量值,且计算量大大减少,处理速度较快,是一种针对长延时的光延迟系统实时测量延迟时间并进行校正的有效方法,易于工程实现。
1 高精度延时测量方法原理分析
已知光纤延迟线中,信号频率与延迟时间有如下关系[8]:
t=φ/(2πf)=(φ0+2πn)/(2πf)
(1)
式中,t是光纤延迟线的延迟时间,f是传输信号频率,φ是输入输出信号之间的相位差,为无模糊值,φ0为模糊相位差,n为相位差模糊数。
对光纤延迟线输入输出信号鉴相得到的相位差存在2π模糊问题,如果可以解得相位差模糊数,就可以利用式(1)得到精确的延迟时间。式(1)得到的延迟时间误差主要来自于相位差测量结果,即:
Δt=Δφ0/(2πf)
(2)
因此在相位差测量误差一定的情况下,提高信号频率可以减小延迟时间测量误差,提高测量精度。
1.1 频域法测量误差的克拉美-罗界
频域法测量延迟时间时,实际是通过对相位差的多次观测来估计延迟时间,通常要求对延迟时间的估计是无偏估计,根据统计估计理论,任意无偏估计的均方根误差不可能低于克拉美-罗界(CRLB)。
观测方程为:
Δφk=2πΔft+nk
(3)
式中,Δφk为第k次观测的相位差,Δf为相邻频点之间的频率之差即频率孔径,tk为测量时间估计值,nk为相位差测量误差,是均值为零、方差为σ2的独立同分布高斯随机噪声。
根据非随机矢量估计的CRLB定义,延迟时间估计值的CRLB可以表示为:
CRLB(t)=(-E(∂lnp(Δφ|t)/∂t2))-1
=(-E∂2/(∂t2)((2πσ2)-(N-1)/2·
=(2π)-2(σ/BW)2(12(N-1)/N(N+1)))
(4)
式中,pΔφt为观测矢量Δφ的条件概率密度函数。故延迟时间估计的均方误差:
Δt1rms≥(CRLBt)1/2
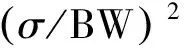
(5)
式中,BW=N-1Δf为观测的信号带宽。
分析式(5)可以看出通过提高频率孔径,可以增加测量点数和提高带宽来获得高的测量精度,带宽一定的情况下测量点数和频率孔径相互制约,而带宽又受到电子系统处理能力的限制。
1.2 线性拟合限定条件分析
考虑频域法利用的是相邻频点的不模糊相位差,测量精度主要受到相位差测量误差的影响,而单频点的无模糊相位差的周期数远远大于相邻频点的不模糊相位差的周期数,相同的相位差误差对延迟时间的影响相对较小,可以有效地提高测量精度。
基于上述思想提出基于线性拟合的方法测量延迟时间。首先使用频域法得到延迟时间t1,通过对ft1取整,利用线性拟合解f频点信号的相位差模糊值n。因为t1的测量值存在误差,对n的估计同样也会出错,偏差为Δn=6Δt1f,·表示向上取整,因此模糊值范围是n-Δn,n+Δn。
根据式(5)得到t1的均方误差,由3-σ准则可知,t1有99.74%的概率落在t1-3Δt1,t1+3Δt1范围内,因此需要通过限定频率范围及模糊数纠正来保证解模糊正确。为了能够判断解模糊是否错误,首先要求3Δt1 f<1/(6Δt1) (6) 根据式(6)来选择频率f的值,t1的误差也有极小可能落在范围之外,为了避免这类错误,需要在选取f时留有一些余量,可取f=0.8/(6Δt1)。但是此时只能保证通过对频点f解得的模糊值错一个周期,由该模糊值与频率f得到延迟时间t2,因为已知t1-t2=3Δt1 1) 根据系统处理带宽BW=N-1Δf合理设置测量点数N与频率孔径Δf,理论上频率孔径越小越好,但点数太多会增加系统负担,因此需要综合考虑。对这N个点测量得到一组原始相位差φ=(φ1,φ2,…,φN),这是消除频率孔径产生的相位模糊之后的值,计算得到延迟时间t1。 2) 利用1.2节分析,选择合适的频点频率f,对ft1取整得到模糊值n。 3) 选择频带内中心频点的原始相位差值φN+1/2根据2Δn+1个n值可以解得一组无模糊相位差值,即: φN+1/2=φ1,N+1/2,…,φ2Δn+1,N+1/2= φN+1/2+2π(n-Δn,…,n+Δn) (7) 这组相位差分别相差一个周期,再由式(1)可以解得一组延迟时间: t2=t2,1,…,t2,2Δn+1=(2πf)-1φN+1/2 (8) 式中,只有一个值为准确的延迟时间。为了求得这个延迟时间的值,由t2的各个分量利用式(1)分别求解其它N-1个频点的有模糊相位差得到2Δn+1组有模糊相位差φ1,…,φ2Δn+1,即φi=(φi,1,φi,2,…,φi,N)i=1,…,2Δn+1。 4) 这2Δn+1组相位差分别由同一个延迟时间得到,因此它们的相频特性都是直线,其斜率就反映了不同的延迟时间,将它们分别与原始测量数据的相位差φ通过下式进行拟合: (9) 由此可得最小的Δi对应的t2,i即为延迟时间,记为t2。 5) 需要进一步提高精度时,增加频点重复2)~4)步。 仿真条件:信号频带为0.9~1.1GHz,频率孔径Δf为10MHz,频率点数N为21。虚线为原始数据φ,实线为5个延迟时间求解得到的5组有模糊相位差φ1,…,φ5,对它们去360°跳变,如图2所示,为了更加直观,没有对相邻频点去模糊处理。 可以看到当信号频率增加,2Δn+1个模糊值对应的延迟时间t2的各分量的差减小,反映在图2中就是各实线的斜率更加接近,会增加出错的概率,这也印证了限定频率范围的正确性。 仿真条件:设延迟时间为4μs,其均方根误差为1ns,处理频带为0.9~1.1GHz,频率孔径Δf为10MHz,频率点数N为21,根据1.2节计算可以得到频率范围是f1<1.61GHz。单频点取1~10GHz频段内每隔200MHz一个点,观察随着频率变化测量精度的变化情况,相位均方误差取1°、5°、10°3个值。每个点做1000次Monte-Carlo试验,仿真结果如图3所示。 从仿真结果可以看到,随着频率的增加测量误差增大,频率较低时测量精度较高,与由仿真条件计算得到的频率条件相互佐证,因此需要限定频率范围。而频率范围内在相位均方误差较大时测量精度也会有所降低,这是因为3-σ准则并不能保证解模糊100%成功导致的,相位均方误差增大会有一定概率解模糊错误,因此对于f1的选择需要保留一些余量。 仿真条件与上节相同中,信号频率为1GHz时可以正确解模糊,因此在得到1GHz信号的延迟时间后,分别用它解6GHz和10GHz信号相位差模糊值,从而提高高频率信号的解模糊成功率,达到提高测量精度的目的,得到的测量精度仿真结果如图4所示。 由图4可以看到对10GHz的单频点信号,延迟时间测量均方误差小于3ps,其精度相比频域法得到较大提高,且瞬时带宽需求低,计算量小。 本文在对频域法的误差分析的基础上,提出了一种高精度实时测量延迟时间的方法,该方法通过线性拟合法解单频点相位差模糊值,得到精确延迟时间,该方法在高精度测量前提下要求的瞬时处理带宽较窄,测量延迟时间的精度高,原理简单,处理速度快,在工程中具有较强实用性。■ [1] 何子述,金林,韩蕴洁,等. 光控相控阵雷达发展动态和实现中的关键技术[J]. 电子学报,2005,33(12):2191-2195. [2] 李希明,黄鹏飞. 多抽头宽带光纤延迟线的设计与分析[J]. 光电技术应用,2012,27(1):45-49. [3] 邱志成.高精度光纤延时技术研究[D].成都:电子科技大学,2009. [4] 闫成至,李尚远,郑小平,等. 低相干光干涉法延时测量中的误差分析[J]. 中国激光,2011,38(1):1-5. [5] 黄涌,李云燕,李流超. 基于TDC技术的光纤延迟时间测试与实现[J]. 光通信技术,2015(3):27-29. [6] 马志超,何翠平,闫军. 高精度远程光纤传输延时测量系统研究[J]. 光通信技术,2015(3):60-62. [7] 徐磊.光控相控阵天线光纤实时延时线设计与测试[D].大连:大连理工大学,2009. [8] 解安国,薛余网,郭建文. 微波光纤延迟线技术研究[J]. 光纤与电缆及其应用技术,2002(4):1-5.2 高精度测量方法具体步骤
3 仿真分析
3.1 线性拟合原理仿真分析
3.2 频率范围条件仿真分析
3.3 高精度测量方法仿真分析
4 结束语
