基于PRI的雷达信号综合分选新方法

李大卫，王晓峰

(1.中国人民解放军95972部队，甘肃 酒泉 735018； 2.空军航空大学信息对抗系，吉林 长春 130022)

0 引言

随着雷达技术体制不断革新和雷达数量的日趋增加，高密度复杂雷达侦察信号的快速有效分选，已经成为制约电子对抗作战效能发挥的瓶颈技术之一。雷达信号分选必须要依据雷达侦察接收机测量的雷达信号参数。目前雷达侦察接收机能够直接测量的雷达信号参数包括载频(RF)、到达方向(DOA)、脉冲宽度(PW)、脉冲幅度(PA)和到达时间(TOA)。其中TOA参数可以转化为雷达信号的脉冲重复间隔(PRI)。

在雷达信号的各个参数中，PRI的变化类型最多、变换范围最大，但同一部雷达辐射信号的PRI具有严格时间相关性，因此PRI是信号分选中最重要的参数。针对PRI信号分选，前人做了很多工作，主要研究成果包括：模板匹配法[1]、累积差直方图法(CDIF)[2]、序列差直方图法(SDIF)[3]、PRI变换[4-5]、修正PRI变换等。然而，这些方法在处理现代高密度复杂信号时，主要存在以下问题：①运算量巨大，难以满足实际需求；②对干扰脉冲和脉冲丢失十分敏感；③无法分选诸如PRI排定、PRI组变等复杂调制信号。

针对PRI分选算法存在的问题，本文提出了一种PRI综合分选新方法。该方法主要由两部分组成：TOA中点匹配和方正弦波插值。首先，采用TOA中点匹配法分选侦察数据中的PRI周期性调制信号；然后，基于方正弦波插值处理TOA中点匹配输出的剩余脉冲，进一步分选出PRI非周期性调制信号(主要是PRI抖动信号)。仿真实验结果表明，该方法能够适应多种PRI调制类型，具备较高的分选准确率，对复杂信号环境具有较好的适应性。

1 TOA中点匹配

设侦察接收机截获的混合脉冲序列为t1,t2,…,tn(n为脉冲序列的总脉冲数)，在脉冲序列长度的中间位置任意选取一点ti，以ti为中心点开始计算其左右两侧相邻脉冲的到达时间差，并进行比较，如果左侧差值大于右侧差值，则计算中心点ti与左侧下一个脉冲之间的间隔值；如果左侧差值小于右侧差值，则计算中心点ti与右侧下一个脉冲之间的差值；如果左右两侧的间隔值相等，则记录该差值，并继续对左右侧下一个脉冲与中心点之间的差值进行比较，直到记录了连续相等的四个差值。

上述匹配方法能够估计出周期性调制信号的PRI值。估计出PRI值后，需要检测该PRI值对应的雷达信号调制类型。类型检测基本原理是：对于非PRI固定的其他PRI周期性调制，一个调制周期内必然有多个脉冲，且本周期内脉冲的TOA值加上骨架周期在下一个周期内必然存在一一对应的脉冲，如图1所示。

因此，通过检测下一周期内是否有脉冲与本周期内的脉冲匹配，就可以判定PRI估计值是否为PRI固定调制。依据PRI调制类型，进行序列搜索，设PRI估计值对应的TOA中点脉冲为tp：

1)对于PRI固定信号。以tp为起点，在左右两侧根据PRI估计值寻找下一个脉冲，检测容差为ε，若找到，将起始点变为找到的脉冲，将其抽取出来。若未找到，继续搜索2倍PRI估计值、3倍PRI估计值，重复上述过程。

2)对于其它周期性调制信号。以tp为检索起始点，在左右两侧后根据PRI估计值寻找下一个脉冲，若存在，将起始点抽取出来，并改变起始点为下一个脉冲；若不存在，继续搜索2倍PRI估计值、3倍PRI估计值，重复上述过程。这种抽取方法可以按照骨架周期一次将该组序列全部提取出来，大大提高了序列检索的效率。

2 方正弦波插值

方正弦波插值算法[6]的主要思想是将离散的到达时间差变换成连续信号，利用傅里叶变换提取出强周期成分后，估计雷达信号的PRI值。将傅里叶变换应用于雷达信号分选能够抑制倍频、抗虚警数据和脉冲丢失，并且由于傅里叶变换拥有各种成熟的快速算法，能够保证信号分选的快速完成。

设雷达侦察序列中相邻脉冲的到达时间差为：

Δti=ti+1-ti,i=1,2,…,N-1

(1)

利用正弦函数进行插值变换：

(2)

经过插值后，离散的到达时间转化为连续的插值函数，本文主要采用方正弦波差值处理PRI抖动信号。下面分析PRI抖动信号插值函数的频谱特征。

PRI抖动信号的PRI值在一个区间内随机变化。可用如下模型定义抖动序列的PRI：

(3)

(4)

当抖动信号的抖动量小于10%，上式可进一步近似为：

(5)

因此，PRI抖动信号的差值函数是幅度和相位都受抖动序列调制的函数。当抖动量小于10%时，反映在频域上就是函数在频谱上会略有展宽，但谱峰位置仍会出现在1/Δt处，这样就能够在频谱中估计出抖动信号的PRI值。

3 算法实现

基于TOA中点匹配和方正弦波插值的PRI综合分选新方法实现框架如图2所示。

4 仿真试验分析

实际侦察的雷达数据是由多种PRI调制类型脉冲的相互交叠构成的，并且存在噪声脉冲和脉冲丢失。为了检验综合分选方法的性能，仿真产生多种复杂体制的交叠脉冲序列，尽可能接近实际侦察信号。共产生了9组不同PRI调制类型的交叠脉冲序列，各组脉冲序列的PRI中心值、PRI变化量及PRI调制方式在表1中给出。所有的脉冲按照到达时间排序，脉冲丢失概率为2%，并且加入了10%的干扰脉冲，共3462个脉冲，采样时间为0.1s。利用综合分选算法对该脉冲流进行50次仿真试验，统计分析其分选结果。

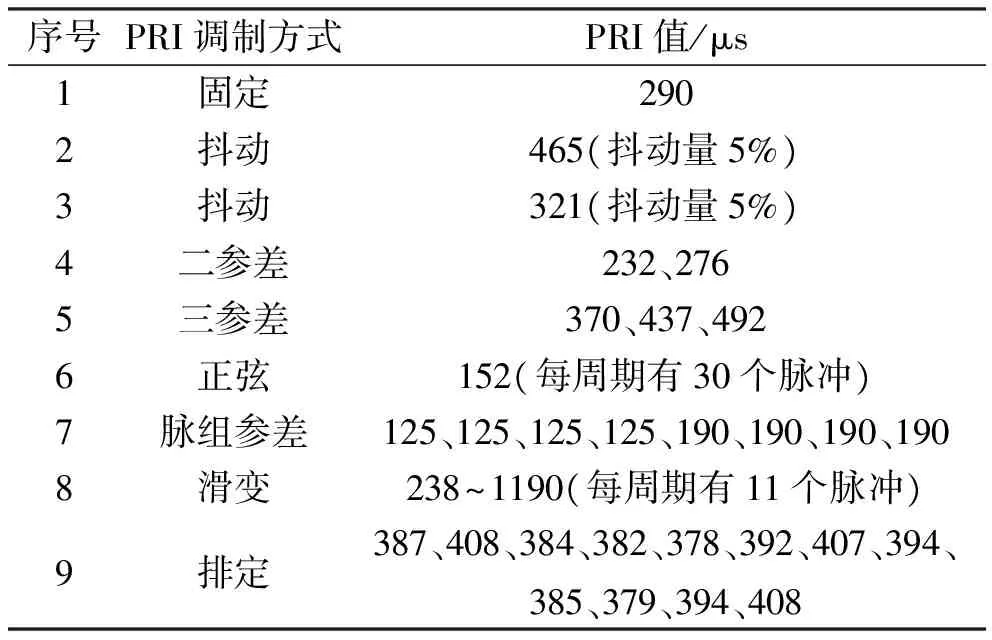
序号PRI调制方式PRI值/μs1固定2902抖动465(抖动量5%)3抖动321(抖动量5%)4二参差232、2765三参差370、437、4926正弦152(每周期有30个脉冲)7脉组参差125、125、125、125、190、190、190、1908滑变238～1190(每周期有11个脉冲)9排定387、408、384、382、378、392、407、394、385、379、394、408

1)首先利用TOA中点匹配法对脉冲流进行分选，分选结果如表2所示。

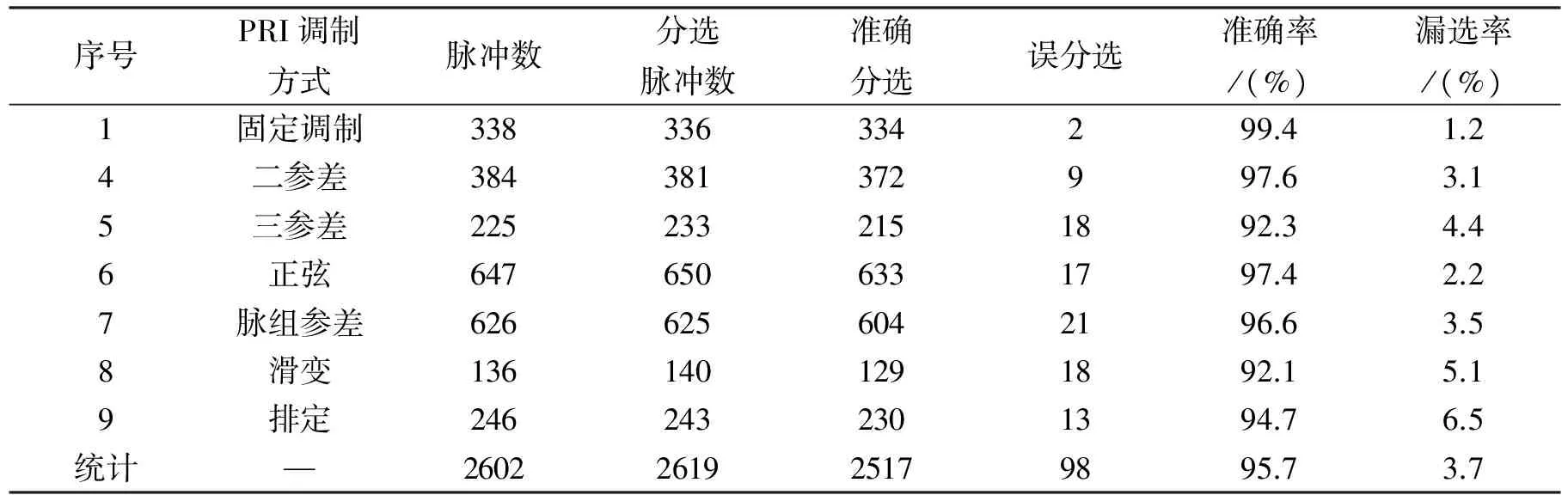
序号PRI调制方式脉冲数分选脉冲数准确分选误分选准确率/(%)漏选率/(%)1固定调制338336334299．41．24二参差384381372997．63．15三参差2252332151892．34．46正弦6476506331797．42．27脉组参差6266256042196．63．58滑变1361401291892．15．19排定2462432301394．76．5统计—2602261925179895．73．7

实验结果表明，TOA中点匹配法能够将第1、4、5、6、7、8、9组脉冲序列分选出来，算法的平均处理时间为3.75s，平均分选准确率为95.7%，平均漏选率为3.7%。在这7组脉冲序列分选出来后，利用TOA差分算法[7]将其PRI调制信息显示在二维平面中，作为调制方式判别的依据。图3显示了第4、5、6、7、8、9组脉冲序列分选结果的TOA差分效果图。可以看出，在正确分选脉冲列的前提下，利用TOA差分法能够将PRI的调制特征曲线清晰地识别出来。

2)经过TOA中点匹配法分选处理后，剩余的主要是PRI抖动脉冲和噪声脉冲，再利用方正弦波插值算法处理剩余脉冲，分选结果如表3所示。

实验结果表明，方正弦波插值算法能够将第2、3组脉冲序列分选出来，平均分选准确率为88.3%，平均漏选率为11.8%。图4为两组PRI抖动脉冲序列分选时的插值函数频谱图(为了观察方便，将脉冲重复频率转化为脉冲重复间隔)，图5为分选出两组抖动脉冲序列的TOA差分效果图。

序号PRI调制方式脉冲数分选脉冲数准确分选误分选准确率/(%)漏选率/(%)2抖动2102111822986．713．33抖动3042912731889．810．2统计—5145024554788．311．8

方正弦波插值估计出的PRI值同真实PRI值存在一定的误差，如图4所示，造成误差的主要原因是PRI周期性调制信号经过TOA中点匹配法抽取后，剩余脉冲序列中的噪声脉冲比例大大增加，影响了方正弦波差值算法的估计精度。

上述实验结果表明，本文提出的综合分选方法能够在复杂信号环境下，对多种PRI调制信号进行有效的分选，平均分选准确率达到92%以上，平均漏选率低于8%，取得了较好的分选效果。在分选结果中虽然存在着少量的漏脉冲和错选脉冲，但这些分选错误并不影响整体PRI调制类型的判别，TOA差分效果图中依然可以清晰地识别出各组PRI的调制规律。

5 结束语

本文研究了基于PRI的雷达信号分选问题，提出了一种综合分选新方法。该方法主要由TOA中点匹配和方正弦波插值组成，能够处理多种PRI调制类型，适用于存在噪声脉冲和脉冲丢失的实际侦察环境。仿真实验结果验证了算法的有效性，该方法具有一定的工程应用价值，为实际雷达侦察信号分选提供了一种新的处理思路。■

[1] Chen Ting, Guo Wei, Shen Bing. A new radar emitter recognition method based on pulse sample figure[C]∥2011 Eighth International Conference on Fuzzy Systems and Knowledge Discovery, 2011: 1902-1905.

[2] Xie Guoliang, Wang Hongxun, Xu Zhongwei,et al. A fast sorting method for modulated and jitter PRI radar signals[C]∥2011 International Conference on Transportation, Mechanical, and Electrical Engineering , 2011: 2210-2213.

[3] Boyacioglu MA, Kara Y, Baykan OK. Predicting bank financial failures using neural networks, support vector machines and multivariate statistical methods: A comparative analysis in the sample of savings deposit insurance fund (SDIF) transferred banks in turkey[J]. Expert Systerms with Applications, 2009, 36(2): 3355-3366.

[4] Nelson DJ. Special purpose correlation functions for improved signal detection and parameter estimation[C]∥Seattle: Proceedings of International Conference on Acoustics, Speech, and Signal Processing, 1993(4): 73-76.

[5] Nishinuchi K, Kobayashi M. Improved algorithm for estimating pulse repetition intervals[J]. IEEE Trans. on Aerospace and Electronic Systems, 2000, 36(2): 407-421.

[6] 蒋勤波, 马红光, 杨利峰．脉冲重复间隔估计与去交织的方正弦波插值算法[J]．电子与信息学报，2007，29(2)：350-354．

[7] 陈维高, 张国毅, 常硕. PRI周期性调制信号的TOA中点匹配分选算法[J]. 现代防御技术, 2014, 42(4): 125-130.