水文序列跳跃变异点的滑动相关系数识别方法

2018-01-21吴子怡桑燕芳袁树堂

水利学报 2017年12期

吴子怡，谢平，2，桑燕芳，雷旭，袁树堂，王超

（1.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072；

2.国家领土主权与海洋权益协同创新中心，湖北武汉 430072；3.中国科学院地理科学与资源研究所陆地水循环与地表过程重点实验室，北京 100101；4.云南省水文水资源局，云南昆明 650106）

1 研究背景

近几十年来，气候变化和人类活动对流域下垫面条件改变所引起的水文效应［1］，已成为全球水循环变化研究的焦点问题。变化环境下，认为水文序列不再来自同一总体，即失去了原有的一致性［2］。对于非一致性的水文序列，若直接采用传统方法进行分析与计算，如水文频率计算，其水文设计结果将存在较大误差，必将增加工程水文设计的风险［3］，同时会对水资源评价、规划、管理等一系列水文水资源问题的研究产生影响［4］。

处理非一致性水文序列时，首要问题是判断其是否存在变异点。变异点主要是指在某个时间位置序列前后变化特性出现显著的差异，存在转折［5］、跳跃［4］等多种表现形式。其中，跳跃变异点反映出水文序列均值发生突变抬升或下降的现象，打破了序列变化的连续性，是非一致性水文序列研究中最关心的问题之一。国内外许多学者围绕跳跃变异点（突变点）的识别问题开展了研究。Kundzewicz等［6］对跳跃变异点识别方法进行了总结和讨论，并指出了各方法的适用条件与优缺点。其中，Mann-Kendall秩次相关法［7-8］与Pettitt检验法［9-10］是两种应用较为广泛的非参数方法。Bayesian变点分析法也被用于水文气象时间序列的跳跃变异点识别［11］。基于Bayesian理论，Lee和Heghinian提出Lee-Heghinian法［12］，主要解决均值跳跃变异点识别问题。Brown-Forsythe检验［13］可减少跳跃变异点分析对数据过多假设的要求［14］，也被用于水文序列的跳跃变异点识别。Li等［15］提出了用可变模糊集方法对滦河流域降雨、径流序列进行跳跃变异点识别。此外，还有大量的相关研究成果与理论方法［16］。然而，从目前研究可以看出，跳跃点识别方法多是从统计学角度进行描述，未能很好地直观反映时间序列跳跃变异的现象和本质，且未能合理考虑跳跃变异点前后均值跳跃幅度、离散程度等因素的影响。因此，实际中需要从序列产生跳跃变异的实质出发，以寻求更加合理有效、易于理解和进行物理成因分析的时间序列跳跃变异点识别方法。

为此，本文借助非一致性序列确定性成分与随机性成分的概念［17］，并以易于求解的相关系数为基础，通过求解跳跃成分与原始序列的相关系数作为跳跃变异点识别指标，提出一种约束条件较少的跳跃变异点识别方法，通过设计统计实验对该方法在不同因素影响下的效率进行讨论，并与常用的Pettitt检验法、Brown-Forsythe检验法进行对比。最后将该方法应用于澜沧江流域允景洪水文站不同时间尺度的径流序列进行跳跃变异点识别与检验，并结合成因分析对所提方法进一步验证。

2 原理与方法

对于任一长度为n的水文序列假设其存在某一跳跃变异点，则整个序列可由变异点分割为长度n1和n2的两段子序列，其中n2段序列存在均值跳跃成分b：

原始序列X与跳跃成分序列Y具有一定的相关性，其相关系数r计算式为：

由式（3）可知，对于某一水文序列，相关系数可能为正或负，当其为正时，原始序列X与跳跃成分序列Y成正相关，表明序列具有向上的跳跃变异；反之，相关系数为负时，表明序列具有向下的跳跃变异。当序列长度和统计特性固定时，其相关系数的绝对值|r|与跳跃变异点前后子序列均值之差呈正相关，相关系数绝对值最大时所对应的点最有可能为跳跃变异点。此外，式（3）还表明，在跳跃变异点的滑动过程中，相关系数还受到序列长度（n），跳跃变异点位置（n1，n2）以及离散程度（σx）的影响。当离散程度较大时，相关系数值较小，而序列长度与变异点位置对相关系数值的影响不能直观从式（3）确定，需结合统计实验等方式加以明确。

实际中，考虑到滑动点位过于靠近首端或尾端时会使得子序列样本容量太小，导致抽样误差太大和结果不可靠，因此利用上述方法进行跳跃变异点诊断时通常不从序列起点开始。本方法中取滑动起始点为10，终点为n-10。

3 不同因素对序列跳跃变异点识别的影响分析

设计多组统计实验，检验所提方法对序列跳跃变异点识别的性能，并分别选取应用较为广泛的非参数检验法——Pettitt检验法［19］与同样具有代表性的参数检验法——Brown-Forsythe检验法［14］进行对比研究。考虑到序列长度、离散程度等因素对跳跃变异点识别均有影响，因此在设计统计实验时分别对各主要因素影响下三种方法的性能进行讨论。生成的模拟序列均假设服从P-III分布，考虑的影响因素包括：序列长度n，跳跃变异点位置系数a，跳跃变异点前后均值变化系数Kave，Cv变化系数KCv，Cs变化系数KCs。跳跃变异点前（后）子序列长度为n1（n2），则表示变异前序列长度占原序列长度的比值，即变异点在序列中出现的位置，取值为（0，1）；跳跃变异点前（后）子序列均值为则离散系数为Cvs（Cvs′），则偏态系数为Css（Css′），则

由于统计实验存在抽样误差，实际中需要考虑相应的误差允许度δ允许（此处取δ允许=0.01）。设各次统计实验结果为对应的已知跳跃变异点位置为各次统计实验序列长度为nk={ }nk|k=1,2,3,…,m，则误差表达式如下：

若δk≤δ允许，认为此次检验有效。将每种方法的有效检出次数与该组实验总次数之比记为该方法在此次实验中的识别效率η（0≤η≤100%）。

3.1 n对跳跃变异点识别的影响设跳跃变异点位于序列中部（a=0.5），且取变异点前序列均值sˉ=500，Cvs=0.4，Css=0.8，取Kave=2，KCv=1，KCs=1。考虑到水文分析与计算时通常要求样本长度大于20，因此取20为序列长度n的下限。令n值分别在20～200，201～400，401～600三组中随机产生，每组生成100个满足上述所有条件的序列，并分别用3种方法进行跳跃变异点检验，结果见表1。

对比表1中不同方法的结果可以看出，随着序列长度增长，各方法的检验效率均有明显提高。滑动R识别法在序列长度不同的3组统计实验中，对跳跃变异点的检验效率与Pettitt检验法、B-F检验法基本相同，部分略有偏高。特别是当n＞200时，无论序列长度n如何延长，3种方法的识别效率都已达到90%以上，可认为此情况下，n的变化将不再对检验结果产生影响。但实际水文分析与计算时，大多数实测水文序列的样本长度在100年以内，因此n=20～200时的识别效率结果显示，提出的滑动R识别法与其他两种常用方法性能相近，均适用于对实际水文序列的跳跃变异点进行识别。

表1 不同序列长度n下3种方法识别效率

3.2 a对跳跃变异点识别的影响取序列长度n=100，变异点前序列均值sˉ=500，Cvs=0.4，Css=0.8，取Kave=2，KCv=1，KCs=1。选取序列9个变异点位置，即令a分别取序列长度的0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，每组生成100个满足上述所有条件的序列，并分别得到3种方法对应的识别效率（图1（a））。

从图1（a）可以看出，当跳跃变异点位置处于序列较中间位置（0.3＜a＜0.7）时，3种方法的识别效率基本相同，均在70%左右。变异点处于较前段（a＜0.3）时，Pettitt方法的识别效率最低，滑动R识别法的效率明显高于Pettitt方法，且较为稳定。变异点处于后段（a＞0.7）时，滑动R识别法的效率升至最高，且高于其他两种方法。整体来看，随着a的变化，滑动R识别法的效率较为稳定且保持在70%～80%左右，并对位于序列尾部的变异点有更好的识别效果，基本不受变异点位置变化的影响。因此，认为对于不同位置的跳跃变异点，提出的滑动R识别法均有较好的识别效率。

图1 3种方法识别效率对比

3.3 Kave对跳跃变异点识别的影响设序列长度n=100、a=1/2，取跳跃变异点前序列均值sˉ=500，Cvs=0.4，Css=0.8，取KCv=1，KCs=1。令Kave分别取1.2、1.4、…、3.0，即-s′=600、700、…、1500，每组生成100个满足上述所有条件的序列，并分别得到3种方法对应的识别效率（图1（b））。从图1（b）可以看出，随着Kave的增大，Pettitt检验法、B-F检验法与滑动R识别法的识别效率均显著增加，且变化幅度区别不大。该结果表明，当序列变异点的跳跃程度越明显时，各方法对跳跃变异点识别的性能均更优，跳跃变异点更容易被识别出。

3.4 KCv对跳跃变异点识别的影响设序列长度n=100，跳跃变异点位于序列中部，取跳跃变异点前序列均值pˉ=500、Cvs=0.4、Css=0.8，取Kave=2、KCs=1。令KCv分别取0.5、1.0、…、3.0，即Cvs′=0.2、0.4、…、1.2，每组生成100个满足上述所有条件的序列，并分别得到3种方法对应的识别效率（图1（c））。从图1（c）可以看出，随着KCv的增大，序列的离散程度增大，Pettitt检验法、B-F检验法与滑动R识别法的识别效率均有明显下降，且下降趋势相近。表明当序列的离散程度增大时，均值跳跃程度会减弱，导致无法更准确地对其进行识别与分离。

3.5 KCs对跳跃变异点识别的影响设定序列长度n=100，跳跃变异点位于序列中部，取跳跃变异点前序列均值sˉ=500、Cvs=0.4、Css=0.8，取Kave=2、KCv=1。令KCs分别取0.5、1.0、1.5、2.0，即Css=0.4、0.8、1.2、1.6，每组生成100个满足上述所有条件的序列，并分别得到3种方法对应的识别效率（图1（d））。从图1（d）可以看出，随着KCs的增大，Pettitt检验法、B-F检验法与滑动R识别法的效率虽略有起伏，但波动不大，基本维持在80%左右，说明该因素对序列变异点识别的影响不大。

结合上述统计实验结果可知，在各因素影响下，滑动相关系数识别法对跳跃变异点的识别效率与常用的Pettitt检验法、B-F检验法基本相同，甚至在有些因素影响下识别效率还略高于另两种方法，且其性能相对稳定。因此，认为本文提出的滑动相关系数识别法可以有效地检验出水文序列的跳跃变异点。此外，Pettitt检验法与B-F检验法均未能如滑动相关系数识别方法直观地反映出水文序列跳跃变异点前后均值跳跃变异幅度、离散程度等的影响。相比较而言，滑动相关系数识别法不仅易于求取，也更便于对跳跃变异点识别结果进行直观判断，还可由相关系数定量分析水文序列中各个参数对跳跃变异识别的影响，进而揭示某一跳跃变异点的出现主要是由哪个水文序列参数的变异所引起的，可为水文变异归因分析提供可靠的依据。

4 实例分析

4.1 研究区概况澜沧江发源于青海省南部的唐古拉山脉，流经青、藏、滇三省（区），于云南省西双版纳州勐腊县出境，出境后称湄公河。允景洪水文站位于西双版纳州景洪市，是澜沧江下游主要控制站（图2），为国家重要水文站（一类精度水文站）。

澜沧江流域水能资源丰富。在云南省境内，允景洪水文站上游的澜沧江干流水利工程建设从1986年开始［20］，至2014年建成投产的大型水利工程有6座。将时间顺序划分为多组开发运行时期（图3）。其中，漫湾水电站具有季调节能力，小湾水电站与糯扎渡水电站是多年调节水库。这些水利工程的建设对澜沧江流域的径流情势造成了较大影响［21］，如大坝截流蓄水对干流年际径流分配的影响，雨季水库蓄水改变洪量带来的径流年内分配变化［22］，特别是径流年内短期变化受干流梯级水电站影响明显［21］。

图2 允景洪水文站位置及流域示意

图3 云南省境内澜沧江干流大型水电站开发运行时间轴

4.2 结果与分析选取允景洪站1956—2014年不同时间尺度的径流序列，采用本文提出的滑动R识别法对各序列进行跳跃变异点检验，同时仍与Pettitt检验法、B-F检验法的结果进行对比。若所提方法与其余两种方法所得变异点一致，则信任该结果；若3种方法所得跳跃变异点存在不一致，则选择识别结果相同的两种方法所给出的跳跃变异点，并结合各结果对应的跳跃成分变化图进行合理性判断。最终得到的各序列跳跃变异点的综合诊断结果见表2。

表2 允景洪站多时间尺度径流序列跳跃变异点识别检验结果

由表2结果可统计出每种方法的有效检出率，即该方法识别结果与综合判断一致的结果数占全部识别结果数的比值。可以得到滑动R识别法对变异点的有效检出率为86.7%，Pettitt检验法为66.7% ，B-F检验法为86.7%。其中，Pettitt检验法在a、e、g、j、k等多个序列中均存在识别误差，而B-F检验法在h、i序列中存在误差，滑动R识别法在c、d序列中存在误差。可见，滑动R识别法在实测水文序列跳跃变异点识别与检验中有很好的效果。再给出综合结果所对应的各序列模比系数（即原始数据与序列均值之比）跳跃成分图（图4），直观反映出跳跃变异点识别的准确性。

为了进一步说明本文所提方法识别跳跃变异点的可靠性，从降水与水电站修建运行两方面着手，分析跳跃变异点出现的物理成因。取允景洪水文站周边5个气象站1957—2014年的年-月尺度降水序列及区域面均降水序列，与处理径流序列相同，也采用上述3种方法对各个降水序列进行跳跃变异点检验，结果见表3。

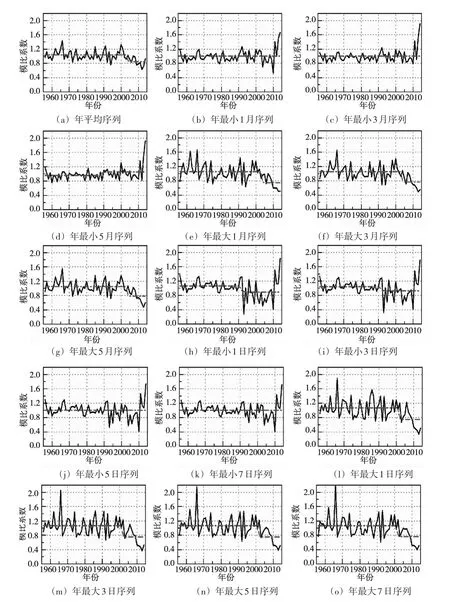
图4 各序列模比系数跳跃成分图

表3 允景洪站周边气象站多时间尺度降雨序列跳跃变异点识别检验综合结果

分析表3可知，除景洪站外，大部分站点及所处区域降水均未出现跳跃变异点。不少学者也对此进行了研究分析［23-24］，认为降水过程变异不是该流域径流变异的主要物理成因。

结合图4与图3对比分析，2004年允景洪站上游糯扎渡水电站与漫湾水电站二期工程开工建设，小湾进行大江截流，其势必对水电站下游的年径流量带来扰动，尽管大朝山水电站已于2003年开始运行，但其水库不具有多年调节性能，因此年径流量仍主要受施工影响，在2004年出现向下的跳跃变异；年最大1、3、5月径流也于2004年出现减少，最小月径流却未减少甚至有所增大（最小5月），说明汛期与枯期的径流量主要受大朝山水电站年内调节作用的影响，且削峰作用更明显。年最大与最小1、3、5、7日径流可反映汛期与枯期的极值情况。允景洪站年最大1、3、5、7日径流序列在2002年左右出现明显减少，说明2002年后，年最大n日洪量被明显削弱，除可能受到小湾水电工程开工的影响外，还反映出漫湾水电站的汛期调蓄效果明显。年最小1、3日径流也在1992年左右出现小幅度跳跃式减小，这应与1992年大朝山水电工程开工以来，一系列水电工程的依次建设有关。

此外，图4还直观地反映出一个普遍现象：在各时间尺度径流序列的尾端（2010年之后），非常明显地显示出汛期径流量减少、枯期径流量增加的特征。这充分说明澜沧江干流多级水电站投入运行后，起到了显著且良好的“削丰补枯”作用。但由于这些变化出现在序列末尾，超出变异点检验方法的应用范围，因此未在检验结果中有所体现。这也说明，无论跳跃变异点识别与检验方法是否有效，都需结合水文序列时序图与物理成因进行分析，才能获得更准确且全面的水文过程变异信息。

5 结论

本文主要提出了水文序列跳跃变异点的滑动R识别方法，在数学公式严格推导基础上，设计一系列统计实验，对影响跳跃变异点识别的多种因素分别进行分析，并与常用的Pettitt检验法、B-F检验法进行识别效率的比较。运用本文所提方法，对澜沧江流域内允景洪水文站的不同时间尺度径流序列进行跳跃变异点识别及检验。结合降水序列变异检测与大型水电工程施工运行情况，对径流过程的突变现象进行成因分析。总结得出以下结论：（1）本文所提滑动R识别法可描述和直观反映水文序列跳跃变异点前后均值跳跃变异幅度、离散程度等因素的影响；采用该方法时，相关系数容易求取，在受到序列长度、变异点位置、均值变化系数、Cv变化系数与Cs变化系数等多种因素影响时，其跳跃变异点识别效率与常用的Pettitt检验法、B-F检验法基本相同，甚至略高，且性能较为稳定。（2）利用提出的滑动相关系数识别法对澜沧江下游允景洪水文站多时间尺度径流序列进行跳跃变异点识别与检验，同时综合Pettitt检验法及B-F检验法的识别结果，以及各序列模比系数跳跃成分变化图得到各序列的跳跃变异点结果。在这些综合检测结果中，滑动R识别法的效率达到86.7%，与B-F检验法相近，但远高于Pettitt检验法的识别效率。（3）结合物理成因分析，认为允景洪站径流变异受降水影响很小，主要与上游一系列梯级水电站的施工与运行有关，且水电站的调蓄作用，特别是年内“削丰补枯”对径流有明显的影响；同时也印证了本文所提方法识别跳跃变异点的可靠性。

本文提出的滑动R识别法可有效识别并检验出水文、气候等时间序列的跳跃变异点，其主要是侧重于对均值变异的识别与检验，是否能有效识别出离散系数Cv和偏态系数Cs的跳跃变异点还需后续作进一步的研究。此外，对于存在多个跳跃变异点的水文序列，可在一次识别后对相应的跳跃性成分进行剔除，再进行二次识别，以此类推，逐一识别出序列的多个跳跃变异点。但其准确率及受序列方差等因素影响的问题还需进一步进行验证。同时还需注意到，不同跳跃变异点识别方法都可能存在一定的误差，因此需要进行物理成因分析，同时将多种方法通过赋权等方式结合使用，尽可能减少和避免单一方法造成的识别误差。

［1］宋晓猛，张建云，占车生，等.气候变化和人类活动对水文循环影响研究进展［J］.水利学报，2013，44（7）：779-790.

［2］宋松柏，李扬，蔡明科.具有跳跃变异的非一致分布水文序列频率计算方法［J］.水利学报，2012，43（6）：734-739.

［3］梁忠民，胡义明，王军.非一致性水文频率分析的研究进展［J］.水科学进展，2011，22（6）：864-871.

［4］谢平等.变化环境下地表水资源评价方法［M］.北京：科学出版社，2009.

［5］陈远中，陆宝宏，张育德，等.改进的有序聚类分析法提取时间序列转折点［J］.水文，2011，31（1）：41-44.

［6］KUNDZEWICZ Z W，ROBSON A J.Change detection in hydrological records—a review of the methodology［J］.Hydrological Sciences Journal，2004，49（1）：7-19.

［7］MANN H B.Nonparametric tests against trend［J］.Econometrica，1945，13（3）：245-259.

［8］BISAI D，CHATTERJEE S，KHAN A，et al.Application of sequential mann-kendall test for detection of approximate significant change point in surface air temperature for Kolkata Weather Observatory，West Bengal，India［J］.International Journal of Current Research，2014，6（2）：5319-5324.

［9］PETTITT A N.A non-parametric approach to the Change-Point problem［J］.Journal of the Royal Statistical Society，1979，28（2）：126-135.

［10］MA Z，KANG S，ZHANG L，et al.Analysis of impacts of climate variability and human activity on streamflow for a river basin in arid region of northwest China［J］.Journal of Hydrology，2008，352（3/4）：239-249.

［11］PERREAULT L，BERNIER J，BOBÉE B，et al.Bayesian change-point analysis in hydrometeorological time series.Part 1.The normal model revisited［J］.Journal of Hydrology，2000，235（3/4）：221-241.

［12］HEGHINIAN S M.A shift of the mean level in a sequence of independent normal random variables：a bayesian approach［J］.Technometrics，1977，19（4）：503-506.

［13］BROWN M B，FORSYTHE A B.Robust tests for the equality of variances［J］.Journal of the American Statistical Association，1974，69（346）：364-367.

［14］ZHANG Y C，ZHOU C H，LI B L.Brown-Forsythe based method for detecting change points in hydrological time series［J］.Geographical Research，2005，24（5）：741-748.

［15］LI J，TAN S，WEI Z，et al.A New method of change point detection using variable fuzzy sets under environmental change［J］.Water Resources Management，2014，28（14）：5125-5138.

［16］DEAN W E，ANDERSON R Y.Application of some correlation coefficient techniques to time-series analysis［J］.Mathematical Geosciences，1974，6（4）：363-372.

［17］丁晶，刘权授.随机水文学［M］.北京：中国水利水电出版社，1997.

［18］邰淑彩.应用数理统计［M］.武汉：武汉大学出版社，2005.

［19］HE T，LU Y，CUI Y，et al.Detecting gradual and abrupt changes in water quality time series in response to regional payment programs for watershed services in an agricultural area［J］.Journal of Hydrology，2015，525：457-471.

［20］王亿春，胡云萍.浅析澜沧江上游水利工程对允景洪水文站水文要素的影响［C］//云南省水利学会2014年度学术交流会论文集.2014.

［21］HE D M，FENG Y，GAN S，et al.Transboundary hydrological effects of hydropower dam construction on the Lancang River［J］.Chinese Science Bulletin，2006，51（B11）：16-24.

［22］钟华平，王建生.澜沧江干流水电开发对径流的影响分析［J］.水利水电技术，2010，41（12）：72-74.

［23］李斌，李丽娟，李海滨，等.1960-2005年澜沧江流域极端降水变化特征［J］.地理科学进展，2011，30（3）：290-298.

［24］尤卫红，何大明，索渺清.澜沧江的跨境径流量变化及其对云南降水量场变化的响应［J］.自然资源学报，2005（3）：361-369.