电动汽车电机总成悬置系统仿真分析及优化

邹小俊，张宝，王在波，刘茵秋，李超

(南京依维柯汽车有限公司，江苏 南京 210028)

全球能源危机、环境污染问题日益严重，纯电动汽车作为新能源汽车的一个重要方向，符合国家节能环保的发展趋势，国内诸多汽车制造厂和研究机构对电动汽车进行了深入研究[1]。电动汽车与传统内燃机汽车的振动噪声源差别较大。传统内燃机汽车的噪声主要来源于发动机噪声、进排气噪声、散热风扇噪声、传动系统噪声、路面轮胎噪声、车身振动噪声和风噪声[2]。电动汽车由于没有发动机噪声和进排气噪声这两大主要噪声，其噪声比内燃机汽车噪声在一般工况下减小很多[3]，但由于电动汽车驱动电机的特殊性，在加速时电机会产生转矩波动，并且瞬时转矩冲击较大[4-6]，这些振动和冲击会传给车架，引起车内振动噪声和部件的疲劳破坏，此时噪声比内燃机汽车噪声要大。

牵引电机通过悬置系统安装在汽车车架上，悬置系统支撑电机的重量，对动力总成与车架间的振动起双向隔离作用[7-9]。驱动电机在工作过程中，在悬置系统某一个自由度方向作用变化的激振力，并引起该方向的振动时，导致其他自由度方向的振动，出现耦合振动。由于耦合振动扩大了振动频率的范围，为了达到相同程度的隔离效果，悬置必须要更软，从而使得稳定性降低。因此，需要对悬置系统进行解耦优化。

目前对电动汽车噪声的研究大部分是沿袭内燃机汽车的控制方式与设计方式，本文建立电机总成悬置系统六自由度模型，计算电机总成悬置系统的固有频率和能量解耦率，并通过改变电机悬置的位置和刚度对电机悬置系统进行仿真优化，以期降低电动汽车悬置系统的振动噪声。

1 模态解耦率计算的基本理论

从能量角度来说，模态解耦是指系统在某个方向的作用力所做的功全部转化为系统在该方向的能量，即沿着某方向的激振力只能引起该方向上的振动[10]。系统的解耦程度通常用模态解耦率来表示，模态解耦率是指在广义坐标上某个模态分配到的动能占系统总动能的比例。在某阶频率下，当模态能量占总能量的98%时，表明该模态能量非常强，也即表明该频率下的该模态占主导地位，其解耦程度非常高。如果各阶模态的解耦率均为100%，表明它们彼此独立，进行系统分析可以将各阶模态当作单自由度系统来处理[11]。

模态解耦率的计算方法如下[12]：

1)计算电机悬系统的固有频率主振型矩阵

固有特性的分析不涉及到外界激振力的影响，因此通常可以将悬置系统简化为自由振动系统，又因为阻尼对系统的固有特性影响较小，因此在固有特性的计算过程中可以忽略阻尼的影响[13]，则系统的振动微分方程为

(1)

式中：M为系统的质量矩阵；q为系统的广义坐标；K为系统的刚度。

式(1)的特征方程为

det(K-ωi2M)=0

，

(2)

式中：ωi为圆频率，rad/s，ωi=2πfi，其中fi为第i阶固有频率，Hz。

通过式(2)计算得到动力总成悬置系统的六阶固有频率f1，……，f6(对应的圆频率分别为ω1，……，ω6)。

系统的齐次线性方程为

(K-ωi2M)Ai=0

，

(3)

将ωi代入式(3)，可求得非零解向量Ai，Ai则为固有频率fi对应的振型向量，从而得到振型矩阵。

2)计算在广义坐标上某个模态分配的动能

第k个广义坐标上分配的动能

(4)

式中：Ai为第i阶振型向量；aik、ail分别为Ai的第k个元素和第l个元素；mkl为系统质量矩阵的第k行l列元素。

3)计算能量解耦率

即计算在广义坐标上某个模态分配到的动能占系统总动能的百分比。第k个广义坐标上分配到的动能占系统总动能的百分比

(5)

2 计算电机悬置系统的结构参数

原车电机采用四点悬置，每个悬置的结构和刚度相同，左右对称，橡胶悬置安装角度相对于整车倾斜30°，电机相对于整车坐标系绕y轴向后倾斜5°。如图1所示。

整车坐标系以电机质心为坐标原点，水平向前为x轴正方向，正上方为z轴，电机质量为180 kg，计算电机质心坐标系下整车的转动惯量Ixx、Iyy、Izz分别为2 525 062、3 091 740、3 091 740 kg·mm2。Ixy、Iyz、Izx均取零。测量悬置点的坐标如表1所示。

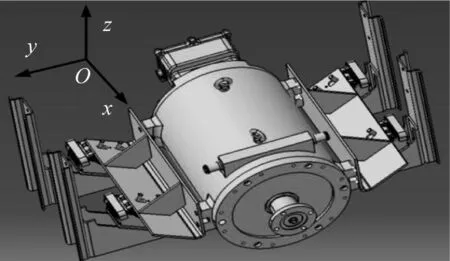
图1 电机悬置结构图

表1 原车电机悬置点坐标 mm

3 建立电机悬置系统仿真模型

图2 悬置系统的ADAMS模型

电机悬置系统一共有沿x、y、z轴方向的平动和绕x、y、z方向的转动6个自由度，因此系统存在6阶固有频率。利用多体动力学分析软件ADAMS建立电机悬置系统的动力学模型,如图2所示。利用Vibration模块计算原系统的固有频率和能量解耦率，计算结果如表2所示。由表2可以看出，原电机悬置系统固有频率为8～34 Hz，大于内燃机汽车(3～25Hz)，绕电机轴线方向(即绕x轴方向)振动的固有频率为33.42 Hz，远大于传统内燃机汽车车。

在某一固有频率下，能量解耦率数值最大的方向为能量占优方向[14]。由表2可知：固有频率为8.53 Hz时，悬置系统在沿x、y、z轴方向的平动和绕x、y、z方向转动6个方向的动能分布分别为88.16%、0.02%、6.25%、0、5.57%、0，说明系统主要沿着x方向振动，即8.53 Hz是悬置系统x方向的固有频率。最理想的情况是，对于系统的每阶固有频率，能量只分布在一个方向上。

表2 原电机悬置系统固有频率和能量解耦率

从表2可以看出:沿x、y轴方向和绕x、z轴方向4个方向固有频率的能量解耦率高于88%，解耦效果良好；而沿z轴平动方向和绕y轴转动方轴解耦率较低，说明存在较严重的振动耦合。悬置系统沿z轴方向振动的固有频率为10.39 Hz，此时系统的能量主要分布在沿z轴平动(59.04%)和绕y轴转动(28.02%)方向；悬置系统绕y轴转动方向的固有频率为20.28 Hz，此时系统的能量主要分布在绕y轴的转动(66.28%)和沿z轴的平动(32.80%)方向，在这两个固有频率下，系统的主要能量同时分散到了两个方向。因此，需要对原悬置系统进行优化，提高沿z向和绕y向振动的能量解耦率，并且保证固有频率合理分配。

4 悬置系统优化方案

1)改变电机的悬置位置

悬置刚度不变，将电机的两个后悬置沿x轴向后平移112 mm。其坐标如表3所示。电机悬置系统的固有频率和解耦率如表4所示。

由表4可知：6个方向固有频率的间隔都大于1 Hz，可以避免频率太近，两个方向同时振动而造成振动耦合[15-16]，满足设计要求(原结构的固有频率的间隔都大于1 Hz)。各个方向固有频率的能量解耦率均高于94%，好于原结构。

表3 电机悬置坐标 mm

表4 电机悬置位置改变后系统的固有频率和能量解耦率

2)改变电机的悬置位置和刚度

改变电机的悬置位置，电机悬置点的坐标同表3。同时，减小电机的悬置刚度。悬置刚度降低后，系统的固有频率减小，有利于隔振。原结构电机悬置系统在x、y、z3个方向的刚度分别为90、100、495 N/ mm，改进后电机悬置系统在x、y、z3个方向的刚度分别为90、90、400 N/ mm。电机悬置系统的固有频率和解耦率如表5所示。

表5 电机悬置位置和刚度改变后系统的固有频率和能量解耦率

由表5可知：电机悬置系统在6个方向的固有频率相对于只改变电机的悬置位置有所降低，有利于提高悬置系统的隔振率，各个方向固有频率的间隔也都大于1 Hz，可以避免频率太近而造成振动耦合。除了沿z轴方向的平动，其他方向固有频率的能量解耦率也较只改变系统的悬置位置时高。

仿真表明，同时改变电机的悬置位置和刚度[17]，优化效果好于只改变电机的悬置位置。

5 电机总成位移及转角校核

参考美国通用汽车公司针对传统燃油汽车拟定的悬置系统28种工况计算规范[18]，制定电动车辆动力总成悬置系统16种工况计算规范表，对动力总成质心的位移和转角进行校核。再根据动力总成质心的位移及转角，分析动力总成的包络面，检查动力总成与其附近零部件的干涉情况。工况表格内容和计算结果较多，这里只列出动力总成质心在x、y、z轴方向的最大位移lx、ly、lz，以及绕x、y、z轴方向转动的最大转角α、β、Γ，如表6所示。

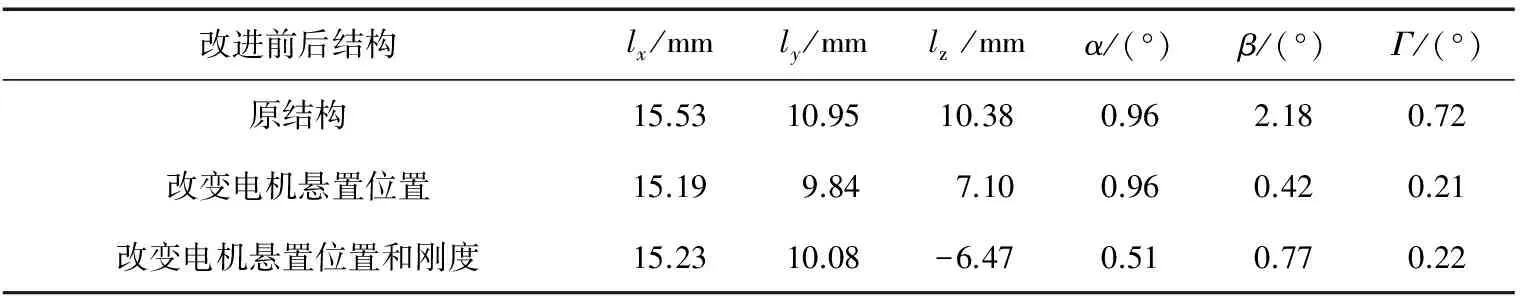
表6 动力总成质心的最大位移和最大转角

从表6可以看出，在16种工况下，只改变电机的悬置位置与同时改变电机的悬置位置和悬置刚度两种方案电机质心的最大位移和转角均小于原结构，说明动力总成与其附近零部件不会发生干涉，满足设计要求。

6 结语

1)利用ADAMS软件建立电机悬置系统六自由度仿真模型，计算得到电动汽车悬置系统固有频率大于传统内燃机汽车，且绕电机轴线方向振动的固有频率远大于传统内燃机汽车，整车竖直方向和俯仰方向存在严重的耦合。

2)在ADAMS软件环境中，采用改变电机的悬置位置、同时改变电机的悬置位置和刚度两种方案对电机悬置系统进行优化，两种优化方案系统各个方向固有频率的间隔均大于1 Hz，可避免频率太近造成振动耦合，系统各个方向的能量解耦率均较原结构有所提高。同时改变电机的悬置位置和刚度后，系统在各个方向的解耦率均优于只改变悬置系统的位置。

3)电机总成位移及转角校核结果表明，改变电机悬置系统的位置和刚度后，电机质心的最大位移和转角均小于原结构，说明电机总成与其附近零部件不会发生干涉，满足设计要求。

[1]徐燚, 吴彰伟.基于ADAMS的某客车动力总成悬置系统分析及优化[J].农业装备与车辆工程, 2013, 51(4):52-57.

XU Yi, WU Zhangwei.Analysis and optimization for automobile powertrain mounting system based on ADAMS[J].Agricultural Equipment & Vehicle Engineering, 2013, 51(4):52-57.

[2]陈南.轿车车身[M].北京：高等教育出版社，2000.

[3]刘显臣.汽车NVH综合技术[M].北京：机械工业出版社, 2014.

[4]曹勇.电动汽车内噪音的分析与控制[D].武汉:武汉理工大学, 2011.

CAO Yong.The analysis and control of electrical vehicle interior noise[D].Wuhan:Wuhan University of Technology, 2011.

[5]GOETCHIUS G. Leading the charge:the future of electric vlectric noise control[J].Sound and Vibration, 2011,45(4)：5-8.

[6]ALKHATIB F.Techniques for engine mount modeling and optimization[D].Milwaukee:University of Wisconsin，2013.

[7]赵立军.电动汽车结构与原理[M].北京:北京大学出版社，2010.

[8]YU Y，NAGANATHAN N G，RAO V D，et al. A literature review of sutomotive vehicle engine mounting systems[J].Mechanism and Machine Theory, 2001，36(1):123-142.

[9]CHO S.Configuration and sizing design optimisation of powertrain mounting systems[J].International Journal of Vehicle Design, 2004, 24(1):172-181.

[10]沈志宏, 郭福祥, 方德广,等. 基于能量解耦法的动力总成悬置系统优化设计[J].噪声与振动控制, 2010, 30(3):35-37.

SHEN Zhihong, GUO Fuxiang, FANG Deguang, et al. Optinal design of powertrain mounting system based on the theory of energy decoupling[J].Noise and Vibration Control, 2010, 30(3):35-37.

[11]吕振华, 罗捷, 范让林.汽车动力总成悬置系统隔振设计分析方法[J].中国机械工程, 2003, 14(3):265-269.

LYU Zhenhua, LUO Jie, FAN Ranglin.Design and analysis method for improving vibration isolation performance of automotive powerplant mounting systems[J].China Mechanical Engineering, 2003, 14(3):265-269.

[12]赵涛.汽车动力总成悬置系统优化设计及软件开发[D].长春：吉林大学, 2005.

ZHAO Tao. Optimum design of engine mounting system and software development[D].Changchun:Jilin University, 2005.

[13]叶向好, 郝志勇.基于MATLAB的发动机总成悬置系统设计研究[J].小型内燃机与车辆技术, 2004, 33(5):12-15.

YE Xianghao, HAO Zhiyong. The study of powertrain mounting system design based on matlab[J].Small Internal Combus-tion Engine and Vehicle Technique, 2004, 33(5):12-15.

[14]黄家铭.中型纯电动客车动力总成悬置系统的优化设计[D].镇江：江苏大学, 2016.

HUANG Jiaming. Optimal design of the powertrain mount system in medium electric bus[D].Zhenjiang:Jiangsu University,2016.

[15]张小红.动力总成悬置系统仿真分析、优化和设计流程[D].长春：吉林大学, 2012.

ZHANG Xiaohong. The simulation analysis and optimization and design process of power-train mounting system[D].Changchun:Jilin University, 2012.

[16]OKWUDIRE C E, LEE J. Minimization of the residual vibrations of ultra-precision manufacturing machines via optimal placement of vibration isolators[J].Precision Engineering, 2013, 37(2):425-432.

[17]侯勇, 赵涛.动力总成悬置系统解耦设计[J].汽车工程, 2007, 29(12):1094-1097.

HOU Yong, ZHAO Tao. A study on decoupling design of engine mounting system[J].Automotive Engineering, 2007, 29(12):1094-1097.

[18]郭荣, 章桐. 汽车动力总成悬置系统[M].上海：同济大学出版社, 2013.