基于线控变传动比的四轮转向汽车最优控制

张庭芳，张超敏，何新毅，曲志林

（南昌大学 机电工程学院车辆工程研究所，江西 南昌 330031）

1 引言

目前汽车转向系统的研究热点由传统的前轮转向（FWS）逐渐转化为四轮转向（4WS）和线控转向（SBW），与前轮转向相比，四轮转向提高了转向操纵机动性和行驶稳定性[1]；而线控转向由于取消了方向盘与转向执行机构的直接连接，具有可以自由设计转向系统的角传递特性和力传递特性的优点[2]。

对于一般意义的汽车理想转向特性而言，要求在保证汽车不会失稳的前提下，低速时具有较高的转向灵敏性和高速时具有较好的转向稳定性[3-4]。但对于采用定转向系角传动比的前轮转向汽车而言，是难以满足这种特性。

研究结合了线控转向和四轮转向的优点，提出了基于线控变传动比的四轮转向汽车最优控制策略，通过反馈四轮转向最优控制器控制变量（横摆角速度）给变传动比控制器，形成闭环控制，控制车辆不会处于失稳状态，变传动比控制器还根据车速变化来控制车辆状态，使汽车处于理想转向状态。四轮转向最优控制器不仅控制汽车横摆角速度的大小，而且控制汽车质心侧偏角基本为零，保证行驶车身姿态。对该方法进行了仿真验证。

2 线控变传动比控制策略

2.1 横摆角速度稳定范围

由于理想的横摆角速度受到路面附着条件的限制，在轮胎附着极限下，侧向力须满足式（1）：

式中：m—汽车质量；ay—侧向加速度；μ—附着系数；g—重力加速度。

当质心侧偏角很小时，车辆的横摆角速度与侧向加速度满足式（2）：

式中：u—车速；ωr—横摆角速度。由（1）和（2）可推出式（3）：

为了保证汽车操纵稳定性，横摆角速度应该有一个范围，且与速度和路面等条件有关，设计的模糊变传动比控制器，应该保证当横摆角速度超出该范围时，尽可能快速把它拉回稳定状态。

2.2 转向系统变传动比控制器设计思路

由于汽车转向系统角传动比与转向盘转角输入和车辆状态等关系非常复杂，很难用精确的数学模型进行表示，而模糊控制是基于规则实时控制的，不需要建立精确的数学模型[5]，所以采用模糊控制方法控制汽车转向系传动比。

采用变转向系传动比的目的是为了实现在保证车辆不会失稳的前提下，具有低速转向灵敏和高速转向迟钝的特性。然而车辆的横摆角速度大小是评价汽车操纵稳定性一个非常重要的指标，所以转向系传动比的大小主要受车速、横摆角速度以及方向盘转角的影响。模糊变传动比控制器设计思路，如图1所示。

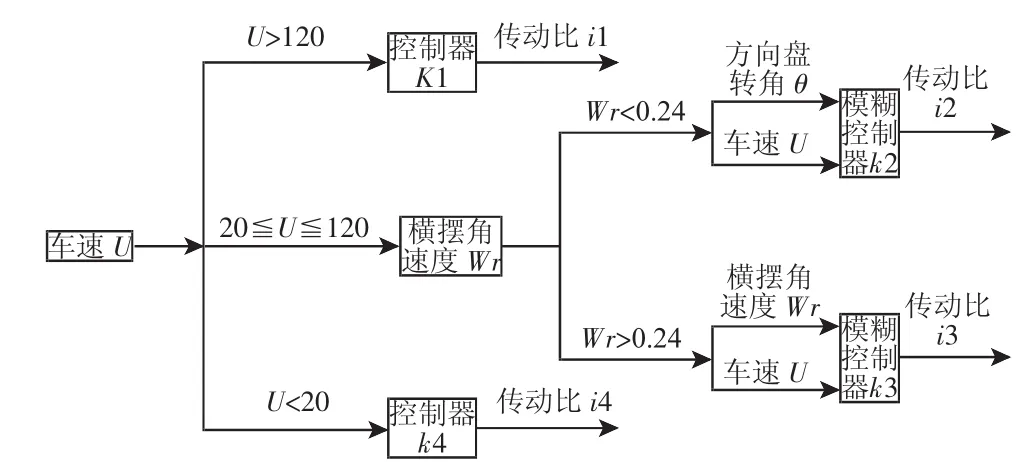
图1 模糊变传动比控制器设计思路Fig.1 The Idea of Variable Transmission Ratio Fuzzy Controlling Design

当汽车速度很高时（评定指标为速度大于120km/h），设置一个大的定传动比，提高汽车操纵稳定性；而速度很低时（评定指标为速度小于20km/h），设置一个小的定传动比，提高汽车转向灵敏度；当汽车速度处于上述两者之间时，通过设定一个横摆角速度稳态安全值，当大于该值时，以控制汽车操纵稳定性为主，以车速和横摆角速度作为控制输入；而小于该值时，以控制提高转向特性为主，以方向盘转角和车速作为控制输入。取附着系数路面附着系数μ为0.816，重力加速度g为9.8m/s2。因为速度u∈［20，120］km/h，所以横摆角速度的附着极限为ωr∈［0.24，1.44］rad/s，在努力提高转向特性的基础上，为安全性考虑取0.24rad/s作为横摆角速度设定值。

2.3 方向盘转角、速度输入变传动比模糊控制器

该控制器主要基于两个原则设计，一是能满足汽车低、高速时对转向系统的要求；二是能满足当汽车高速时，由于转向盘转角集中在中间转向区较小的范围内，将转向盘中间位置设成大传动比，降低车辆的操纵轻便性；而当汽车中低速时，转向盘转角可能会很大，此时应满足传动比随着转向盘转角的增大而迅速减小，可以让驾驶员轻松完成转向[5]。模糊控制规则：输入车速u的工作范围（20-120）km/h；考虑到输入转角的对称性，本次研究取转角为正的那一半，方向盘转角θ工作范围（0-540）°；传动比ic的工作范围（8-24）。这里将u、θ和ic的模糊输入语言分成七个级别，NB（负大）、NM（负中）、NS（负小）、Z（零）、PS（正小）、PM（正中）、PB（正大）。 其中：u=｛5.55，10.18，14.81，19.44，20.07，28.7 33.33｝m/s，θ=｛0，1.57，3.14，4.71，6.28，7.85 ，9.42｝rad，ic=｛8，10.67 13.33，16，18.67，21.33，24｝，分别对应｛NB NM NS Z PS PM PB｝级别。方向盘转角、速度输入变传动比模糊控制规则（简写为模糊规则1），如表1所示。

2.4 横摆角速度、速度输入变传动比模糊控制器

该控制器准则是在中低速时，传动比基本跟随横摆角速度的节奏变化，但是随着速度的增加传动比的上升速度需显著提高，因为横摆角速度的附着极限在迅速减小，此时以操纵稳定性为主。模糊规则；输入速度u的工作范围（20～120）km/h；横摆角速度的工作范围（0.24～1.5）rad/s；传动比 ic的工作范围（8～24）。u=｛5.55 10.18 14.81 19.44 20.07 28.7 33.33｝m/s，θ=｛0.24 0.45 0.66 0.87 1.08 1.29 1.5｝rad/s，ic=｛8 10.67 13.33 16 18.67 21.33 24｝，分别对应｛NBNM NS Z PS PM PB｝规则。横摆角速度、速度输入变传动比模糊控制规则（简写为模糊规则2），如表2所示。

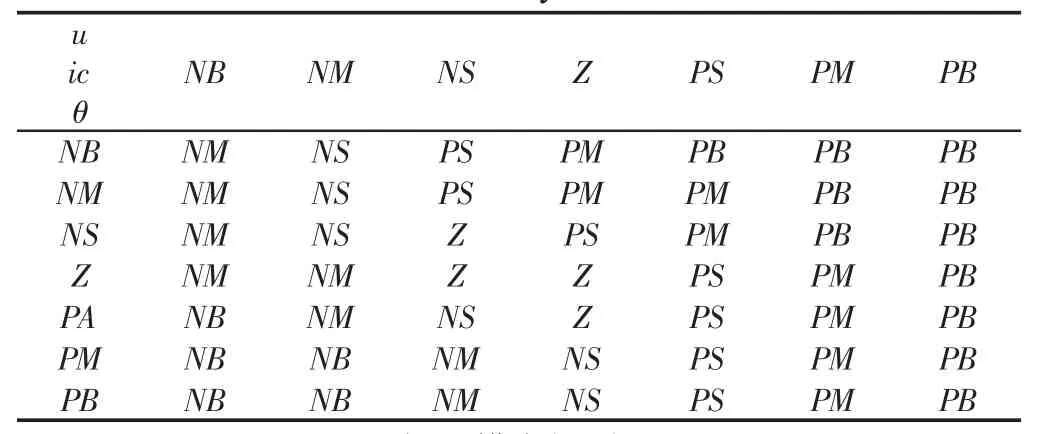
表1 模糊规则1Tab.1 Fuzzy Rule 1

表2 模糊规则2Tab.2 Fuzzy Rule 2

3 四轮转向最优控制

3.1 四轮转向汽车横向动力学模

质心侧偏角和横摆角速度是影响汽车转向稳定性的两个至关重要的因素[6-7]，把汽车模型简化为一个二自由度两轮模型进行研究，理论和试验证明[8]，在正常车速范围内的非紧急状态和小转向角条件下，该模型能以很好的精度表征车辆转向的实际物理过程。假设轮胎侧偏特性处于线性范围，保持汽车前进速度，忽略悬架的影响，认为汽车只作平行于地面的平面运动，则汽车只有沿y轴的侧向运动与绕z轴的横摆运动2个自由度。其运动方程如下：

式中：β—质心侧偏角；kf、kr—前、后轮侧偏刚度；δf、δr—前、后转角；a和b—质心到前、后轴的距离；IZ—汽车绕质心的转动惯量。为了可以调节前、后轮最优控制反馈角的比例[9]，令前后轮转角满足式（5）

式中：δf—方向盘转角经过变传动后传给前轮的输入转角；δi—控制器反馈输入角；ki—控制器对前后轮输入分配比。

把式（5）代入（4），并化为状态方程：

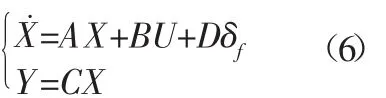
3.2 四轮转向最优控制器设计

构造最优控制器的目的是寻求最优的控制器反馈输入角，使质心侧偏角为零和横摆角速度响应快速而稳定，并控制所需的能量较小，所以应使式（7）二次型性能指标为极小值。

构造哈密顿函数H为：

因为只要汽车参数确定，R和B都为常数，所以只要γ（t），就可求出 U*：γ（t）=P（t）X-ε（t） （10）

对（10）两边求导可得：

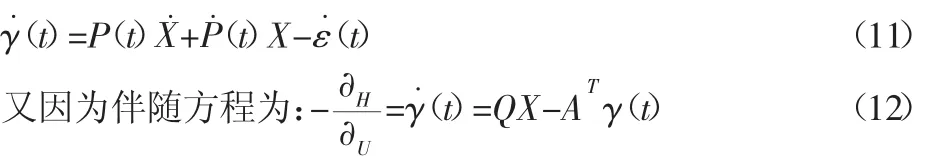
令式（11）与式（12）相等，并把式（6）、式（9）和式（11）代入，考虑到 A、B、Q、R 都为常数阵，当 t→∞ 时，p˙（t）=0，ε˙（t）=0，得：

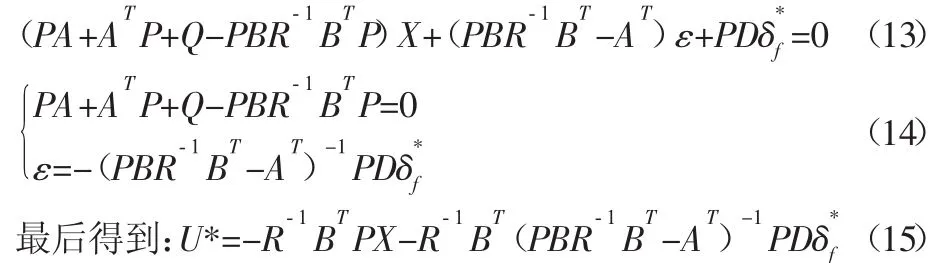
所以最优控制器前轮转角前馈增益矩阵K1=-R-1BT（PBR-1BT-AT）-1PD，而状态变量反馈增益矩阵K2=-R-1BTP。四轮转向最优控制器系统结构，如图2所示。

图2 四轮转向最优控制器系统结构Fig.2 Optimization Controller System Structure of Four-Wheel Steering

4 仿真设计与分析

运用MATLAB/Simulink对上述线控变传动比四轮转向最优控制建模仿真，并与相同参数的前轮转向、定前后轮转向比四轮转向（简称比例型四轮转向）以及线控定传动比最优控制四轮转向（设定i为14）仿真对比，建立模型，如图3所示。比例型四轮转向前后轮转角比值是基于保证稳态质心侧偏角为零设计的[10-11]：

建模样车具体参数[7]为：m=1359.8kg，a=1.063m，b=1.485m，IZ=1992.54kg·m2。取控制器对前后轮反馈分配比ki为0.5，加权矩阵当汽车高速行驶时，转向盘转角一般集中在中间转向区较小的范围内，转角不会很大；而中低速时，转向盘转角变换可能会很大，所以采取四种情况做仿真对比：（1）低速、低转角（u 为 30km/h，θ为 50°）；（2）低速、高转角（u 为 30km/h，θ为 300°）；（3）高速、低转角（u 为 120km/h，θ为 50°）；（4）高速、中转角（u为30km/h，θ为100°）。当取速度为30km/h时，前馈增益，反馈增益 K2=［-48.0406，0.0295］；而取速度 120km/h，前馈增益，反馈增益。四种情况仿真结果，如图4～图7所示。

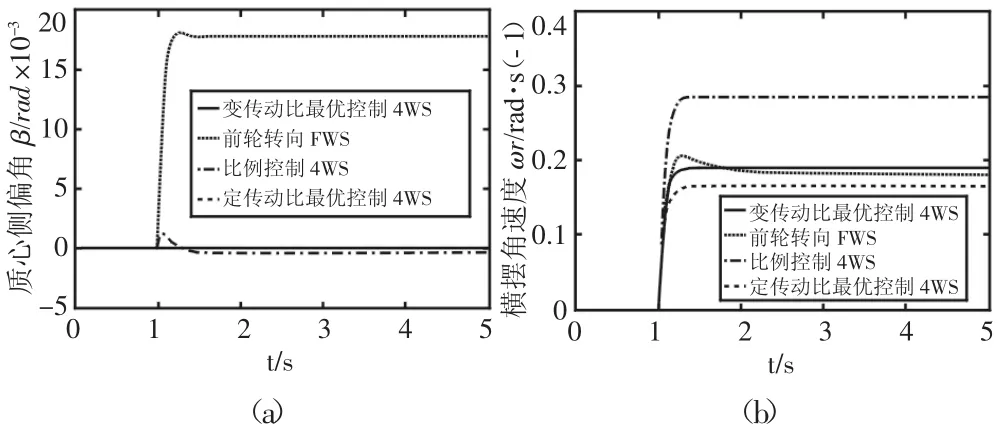
图4 低速、低转Fig.4 Low Speed，Low Angle

图5 低速、高转角Fig.5 Low Speed，High Angle

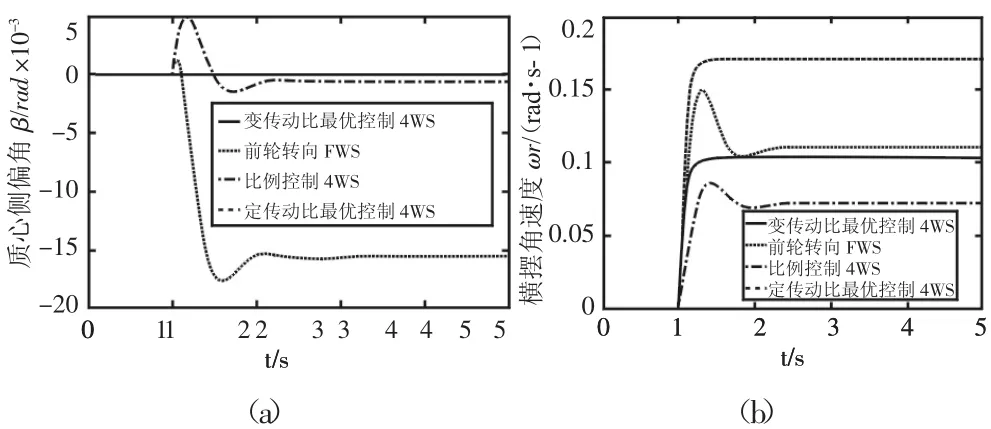
图6 高速、低转角Fig.6 High Speed，Low Angle

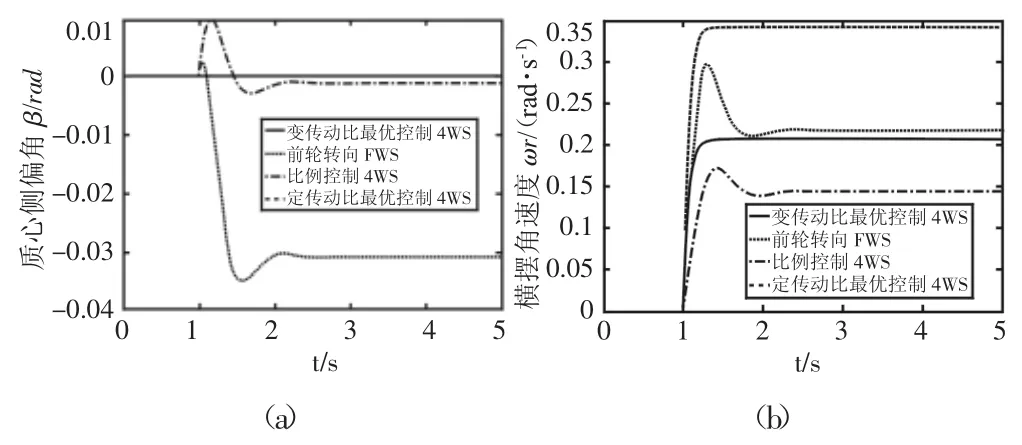
图7 高速、中转角Fig.7 High Speed，Medium Angle

上述四种情况质心侧偏角和横摆角速度稳态值（简写为稳态值），如表3所示。

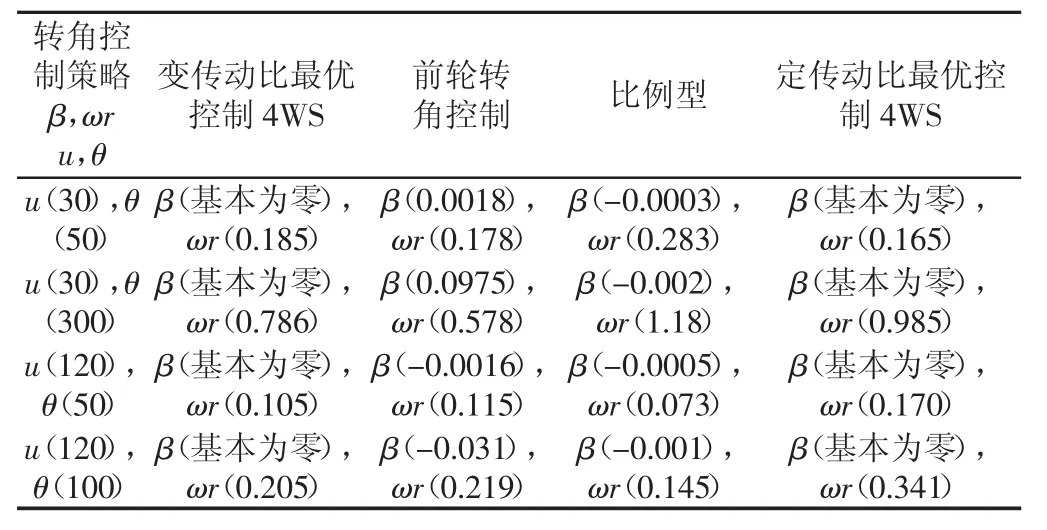
表3 稳态值Tab.3 Steady Value

表中：β 单位（rad）；ωr单位（rad.s-1）；u 单位（km.h-1）；θ单位（°）。

从质心侧偏角仿真结果可知，四种情况都说明最优控制车辆车身姿态保持能力要强于前轮转向和比例型四轮转向控制车辆，而比例型控制车辆要好于前轮转向车辆。从横摆角速度仿真结果可知：（1）低速、低转角时，采用变传动比最优控制车辆（0.185 rad/s），转向轻便性要比前轮转向（0.178rad/s）和定传动比最优控制车辆（0.165rad/s）好；（2）低速、高转角时，由前面横摆角速度附着极限条件可知，0.96rad/s，所以比例型控制（1.18rad/s）和定传动比最优控制车辆（0.985rad/s）要大于附着极限，这种情形车辆很容易发生侧滑，甚至导致侧翻。而前轮转向控制车辆横摆角速度值（0.578 rad/s）虽然最小，但经过了一定的超调量，所以结果表明：在低速、高转角时采用变传动比最优控制车辆（0.786rad/s）操纵稳定性要好于比例型控制和定传动比最优控制车辆，而在保证车辆安全性的前提下，其灵活性要优于前轮转向控制车辆；（3）高速、低转角时，变传动比最优控制车辆（0.105rad/s）操纵稳定性要优于定传动比最优控制车辆（0.115rad/s）和前轮转向车辆（0.170 rad/s），而虽然比例控制车辆横摆角速度最小（0.073rad/s），但经历了一个较大的超调量；（4）高速、中转角时，此时由于横摆角速度附着极限条件为0.32rad/s，而定传动比最优控制车辆横摆角速度（0.341rad/s）超过了附着极限，这种情况是很危险的，仿真结果表明：高速、中转角时，变传动比最优控制车辆（0.205rad/s）操纵稳定性要优于定传动比最优控制车辆和前轮转向车辆（0.219rad/s），而虽然比例控制车辆横摆角速度最小（0.145rad/s），但经历了一个较大的超调量，使其达到稳态的时间延长。

5 结论

通过分析基于线控转向变传动比最优控制策略的优点，设计相应的变传动比模糊规则以及四轮转向最优控制器，并对其进行仿真对比验证，仿真对比结果表明这种方法实现了两个重要特性：（1）在保证汽车不会失稳的前提下，低速时具有较高的转向灵敏性和高速时具有较好的转向稳定性的特性。（2）不仅使车辆质心侧偏角基本为零，保证了汽车行驶姿态，而且使横摆角速度瞬态响应的超调量很少，达到稳定时间缩短。

［1］何辉，王鹏.基于最优控制的三自由度四轮转向研究［J］.辽宁工业大学学报：自然科学版，2012，32（1）：31-34.（He Hui，Wang Peng.Study on Three Degrees of Freedom for Four-wheel Steering Vehicle Based on Optimal Control［J］.Journal of Liaoning University of Technology：Natural Science Edition，2012，32（1）：31-34.）

［2］郑宏宇，宗长富，田承伟.基于理想转向传动比的汽车线控转向控制算法［J］.吉林大学学报：工学版，2007，37（6）：1229-1235.（Zheng Hong-yu，Zong Chang-fu，Tian Cheng-wei.Control algorithm for steer-by-wire system with ideal steering ratio［J］.Journal of JilinUniversity：Engineering Edition，2007，37（6）：1229-1235.）

［3］姚江云，孔峰，吴方圆.基于变传动比的线控转向前轮转角控制［J］.计算机测量与控制，2012，20（8）：2018-2113.（Yao Jiang-yun，Kong Feng，Wu Fang-yuan.Control for or Front Wheel Angel of Steer-By-Wire based on Intelligent Variable Streeing Ration［J］.Computer Measurement&Control，2012，20（8）：2018-2113.）

［4］王春燕，崔滔文，赵万忠.基于理想传动比的主动前轮转向控制［J］.农业工程学报，2015，31（4）：85-90.（Wang Chun-yan，Cui Tao-wen，Zhao Wan-zhong.Active front wheel steering control based on ideal transmission ratio［J］.Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE），2015，31（4）：85－90.）

［5］杨胜兵.线控转向系统控制策略研究［D］.武汉：武汉理工大学，2008.（Yang Sheng-bing.Steer-by-wire System Control Strategy Research［D］.Wuhan.Wuhan University of Technology，2008.）

［6］邱浩，雷正保，贺萍.基于变传动比的后轮主动转向控制方法研究［J］.机械设计，2015，32（1）：90-94.（Qiu Hao，Lei Zheng-bao，He Ping.Research on active steering control of rear wheels based on variable transmission ratio［J］.Journal of Machine Design，2015，32（1）：90-94.）

［7］杜峰，闫光辉，魏朗，陈涛.主动四轮转向汽车最优控制及闭环操纵性仿真［J］.汽车工程，2014，36（7）：848-852.（DuFeng，YanGuang-hui，WeiLang，ChenTao.OptimalControlandClosedloop Controllability Simulation for Active Four-wheel Steering Vehicle［J］.Automotive Engineering，2014，36（7）：848-852.）

［8］Smith D E，Starkey J M.Effect of model complexity on the performance of automated vehicle steering controllers：model development，validation and comparison［J］.Vehicle System Dynamics，1995，24（2）：163-181.

［9］张孝祖.车辆控制理论基础及应用［M］.北京：化学工业出版社，2006（10）.（Zhang Xiao-zu.Fundamentals and application of vehicle control theory［J］.Beijing：Chemical Industry Press，2006（10）.）

［10］杜峰，魏朗，赵建有.基于状态反馈的四轮转向汽车最优控制［J］.长安大学学报：自然科学版，2008，28（4）：91-94.（Du Feng，Wei Lang，Zhao Jian-you.Optimization control of four-wheel steering vehicle based on state feedback［J］.Journal of Chang，an University：Natural Science Edition，2008，28（4）：91-94.）

［11］周丽，王翠，欧林立.基于模糊控制的四轮转向汽车研究［J］.机械与电子，2009（3）：40-42.（Zhou Li，Wang Cui，Ou Lin-li.Research on Four-wheel-steering Vehicle Control Based on Fuzzy Control［J］.Machinery&Electronics，2009（3）：40-42.）