影响铰接式自卸车操纵稳定性的结构参数分析
2018-01-19郭晓波
翟 雁 ,郭晓波 ,张 江
(1.安阳工学院 机械工程学院,河南 安阳 455000;2.安阳工学院 计算机科学与信息工程学院,河南 安阳 455000;3.安阳鑫盛机床股份有限公司,河南 安阳 455000)
1 引言
操纵稳定性是影响行驶中的车辆操纵方便程度的重要性能,同时也是对车辆高速行驶时安全性擦产生影响的主要性能。从动力学系统角度上来看,铰接式自卸车与小轿车、普通货车辆有很大的差别,表现在质心位置高,空载及满载时前后及左右方向的载荷转移大,轮胎及悬架系统的刚度大,操纵转向响应时间长等方面[1]。由于车辆操纵稳定性的影响因素涉及到多个方面,简单模型的计算难以从多方面表达实际车辆的操纵稳定性,与实际结论也将会有较大差别。为准确描述车辆行驶过程中表现出的操纵稳定性、动态特性,需要根据铰接式自卸车结构特点,建立此类车辆的操纵稳定性研究模型,对车辆的操纵稳定性进行研究。
国内外学者对车辆操纵稳定性的研究取得了一定的成果:文献[2]对悬架运动学影响整车性能的因素进行了深入的分析,并重点分析了轮胎对整车操纵稳定性的影响;文献[3]基于虚拟样机技术对悬架性能进行分析,并研究其对整车操纵稳定性和平顺性的影响;文献[4]采用多刚体动力学法,搭建了某款汽车的7自由度振动分析模型,将各态历经的随机路面谱作为输入,研究其对整车操纵稳定性的影响;文献[5]用分析力学的方法,考虑人体、车身、路面等的实际状态,依托动力学普遍方程获得多自由动全系统模型,设计主观评判条件,以此来对整车操纵稳定性进行分析评价。根据铰接式自卸车的结构特点和性能特征,基于多体系统动力学原理,搭建6自由度的整车操纵动力学分析模型。当车辆在满载与空载工况运行时,在角阶跃输入下,对影响整车操纵稳定性进行分析,对影响其的各状态参量的瞬态和稳态响应进行分析。选取整车的前后轮胎参数、悬架系统参数、车辆的轴距、铰接点位置等发生变化时,各状态参量的响应情况进行分析,以此研究其对整车操纵稳定性的影响。
2 铰接式自卸车多刚体模型
铰接式自卸车整车模型和多刚体系统简化模型,如图1所示。铰接式自卸车结构参数,如表1所示。模型建立如下:B1为后轴,B2为后簧载质量,B3为前簧载质量,B4为前轴部分,铰接式自卸车可看作为由两轴支撑,除地面外共有4个刚体组成的多刚体系统;mi为刚体Bi的质量,并记整车质量m=sum(mi)(i=1、2、3、4)[6];在简化假设过程中,忽略连接件尺寸和质量,将转向铰接点与摆动环简化为具有两个转动自由度的一个铰点,实现转向和绕摆动环轴线的转动;建立四个坐标系分别为 H0、H1、H2、H3、H4分别为地面、B1、B2、B3、B4等处,所对应的各坐标系写作e-ij(i=0、1、2、3、4),j=1、2、3代表坐标系的三个方向。B0与B1之间由H1连接,具有三个自由度;B2与B3之间由H3连接,具有两个转动自由度[7]。

图1 铰接式自卸车模型Fig.1 Model of Articulated Dump Truck
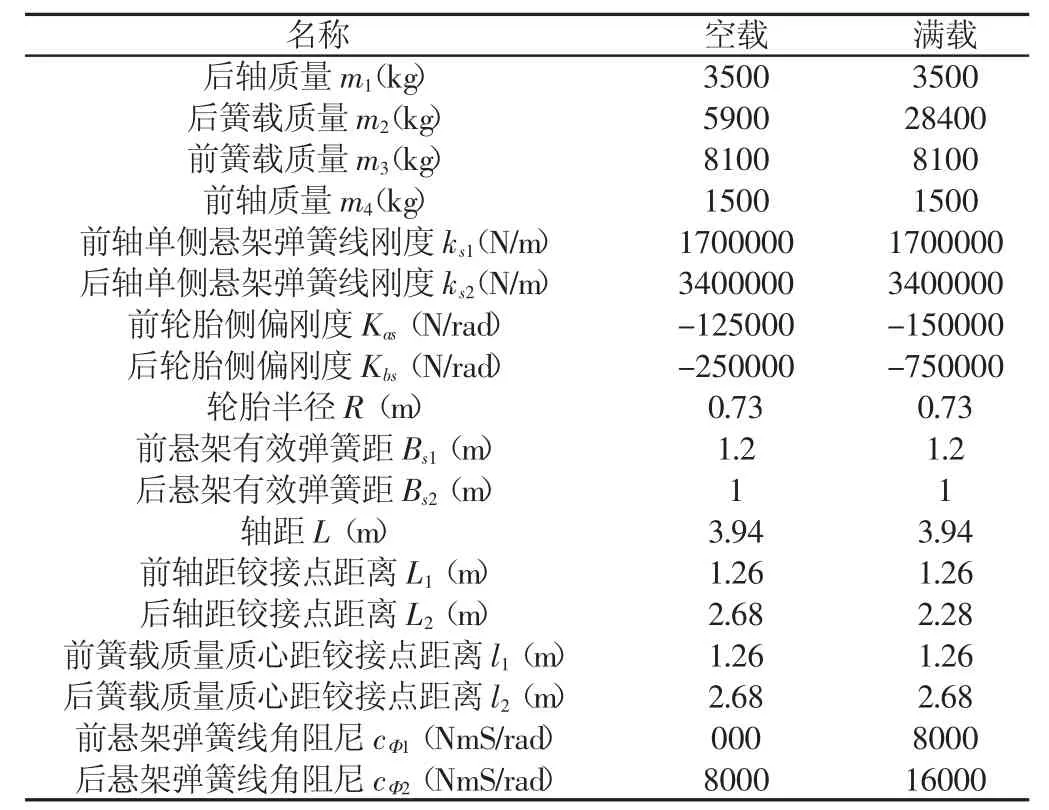
表1 铰接式自卸车参数Tab.1 Parameters of Articulated Dump Truck
2.1 整车受力分析
整车模型系统中,内力主要来自转向铰接点H3,以及关联悬架系统的铰H2与铰H4。不计铰H3处摩擦力的作用,H3主要传递ADT两侧转向油缸伸缩产生的扭矩。车辆发生转向时,前车体对后车体的作用扭矩Mδ通过H3传递,其使得前、后车体绕铰接点分别转过 δ1、δ2,即该力矩使轮胎 A、B 产生侧偏角 δ1,使轮胎 C、D产生侧偏角δ2,并且该力矩引起的前、后轮胎所产生的侧向力对铰接点的力矩相等,方向相反[8]。记轮胎的侧偏刚度分别为kas、kbs、kcs、kds,k1、k2分别为前后轴轮胎的总侧偏刚度,则:
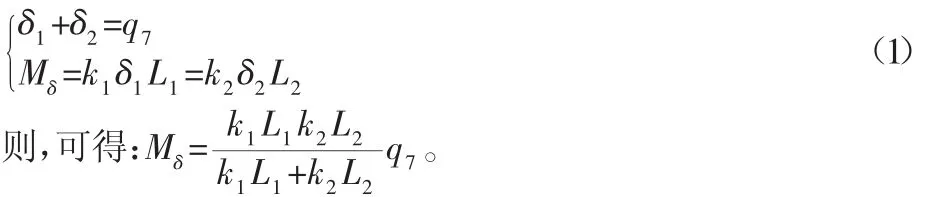
式中:h1、h2—C2与 H2、C3与 H3之间的垂直距离,m;l1、l2—C2、C3与铰接点之间的水平距离,m;h—H2与C4、C1之间的垂直距离,m;L1、L2—铰接点与前、后轴之间的距离,二者之和记为L,m;B—轮距,m;R—轮胎半径,m;ks1、ks2—前后的单个悬架刚度,N/m;Bs1、Bs2—前、后悬架有效弹簧距,m;K1、K2—悬架的线性刚度,N/m;KΦ1、KΦ2—前后侧倾角刚度,N/m。整车所受的外力主要包括自身重力、地面对轮胎的作用力以及离心力[9]。
转弯行驶时,ρ1、ρ2分别为前、后车体的转弯半径,则整车各
2.1.2 轮胎垂直径向力
不考虑簧载质量侧倾时,求出整车簧载质量重力对各轴所施加的垂直力。设作用在前、后轴上的垂直力分别为N1、N2,忽略小角度转向运动对各轴承受簧载质量垂直作用力的影响[10],则整车静力平衡方程(对N1作用点取矩及垂直方向受力平衡),则:

转弯时,各轮所受垂直径向力变动值为:

式中:g—重力加速度。
2.1.3 轮胎侧向力
车辆的左、右前轮转向角均较小,视为相等,记为δ,则有:

式中:VA、VB、VC、VD分—轮胎质心处的速度。
则系统外力主矢及相对质心主矩列阵分别为:
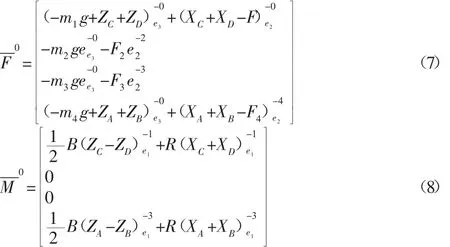
2.2 整车多体动力学模型
根据分析,则铰接式自卸车派生树系统多刚体动力学模型方程可写作:

式中:H1处为3自由度复合铰接点,H2、H3、H4处为2自由度复合
铰接点,则系统共有9个自由度,故其广义坐标列阵为:

将式(10)带入式(9)可得铰接式自卸车多刚体动力学模型方程:

2.3 整车稳定行驶条件
车辆稳定行驶条件,在没有输入的情况下,动力学方程中,k16、k26、k46、k56、k66均为 0,且q˙7=q¨7=0,此时,将动力学方程组式(10)第三方程除去,并进一步将其转变为一阶齐次方程组[11]:

式(13)对应齐次方程特征方程展开式为:
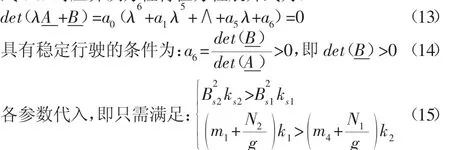
3 整车角阶跃输入转向响应
车辆转向过程中,角阶跃输入为5°,车辆的运行速度为10m/s,各状态参量在空载与满载时的响应曲线。根据多刚体动力学获得前车节横摆角速度和前轴质心侧向速度的响应分别与后车节横摆角速度和后轴质心侧向速度的响应相似。稳态时,铰接式自卸车前、后簧载质量的侧倾角速响应的取值均为0,整个过程呈现出振荡衰减函数形式,空载时前、后簧载质量侧倾角速响应过渡时间分别为0.5s、0.7s,而满载时前、后簧载质量侧倾角速响应过渡时间分别为0.8s、1.3s,符合车辆行驶特点。在此状态下,各参数稳态取值,如表2所示。
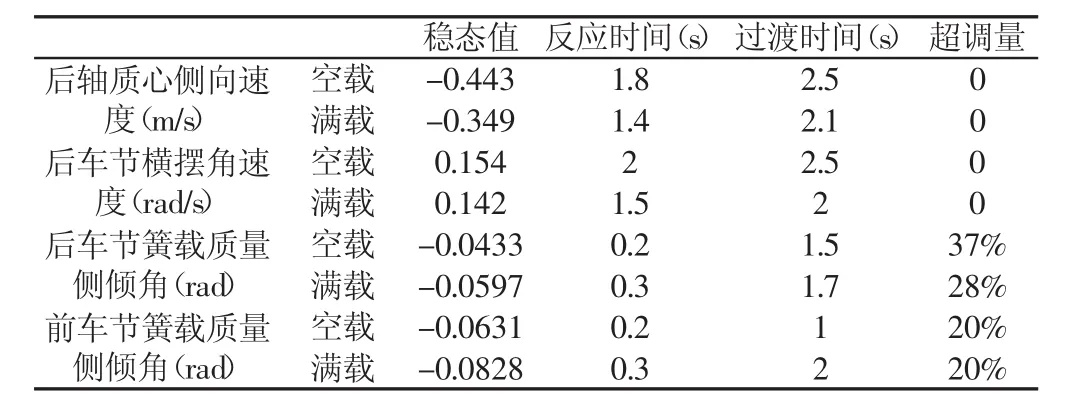
表2 各状态参量的响应指标Tab.2 Response Index of Each State Parameter
4 参数对操纵稳定性影响分析
4.1 轮胎侧偏刚度
4.1.1 前轮胎侧偏刚度k1
铰接式自卸车在k1以5%幅度变化时,状态变量响应曲线图略。铰接式自卸车前轮侧偏刚度变化时各状态参量的稳态值,如表3所示。
4.1.2 后轮胎侧偏刚度k1
经计算当k1变化时,其对前后簧载质量的侧倾角速度影响较小,在后轮胎侧偏刚度k2按5%递增、递减变化时,后轮侧偏刚度变化时各状态参量的稳态值,如表4所示。
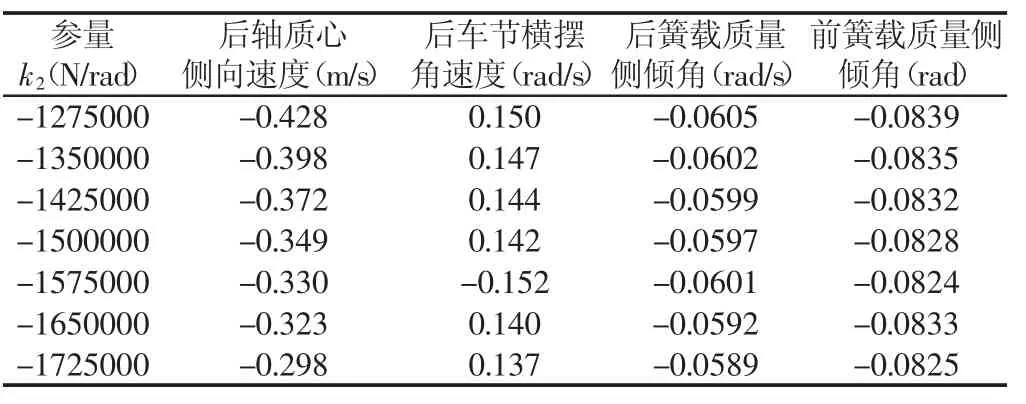
表4 后轮侧偏刚度变化时各状态参量的稳态值Tab.4 Steady-State Values of Various State Parameters
4.2 悬架刚度
在前、后悬架单侧刚度按5%递增、递减变化时,对簧载质量侧倾角速度及簧载质量侧倾角度响应的影响情况,图略。前、后悬架单侧刚度按5%递增、递减变化,ks1按比例增大时,其前、后簧载质量侧倾角速度的振动幅值和稳态值也均增大,并有相同的变化趋势,但均不成线性关系,前悬架刚度对前、后簧载质量侧倾角稳态值的影响。当ks1增大时,簧载质量的侧倾角速度的反应时间缩短而其过渡时间增加;当ks2按比例增大时,簧载质量侧倾角速度的振动幅值和稳态值均减小,且均不成线性关系,也有相同的变化趋势,后悬架刚度对前、后簧载质量侧倾角度稳态值的影响。
4.3 轴距
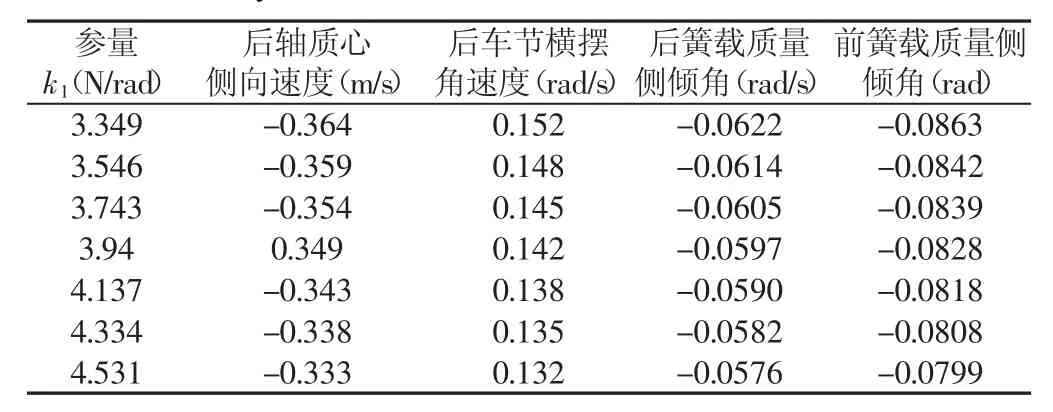
表5 轴距变化时各状态参量的稳态值Tab.5 Steady-State Values of Various State Parameters
铰接式自卸车轴距大小与铰接点的位置紧密联系,它们共同影响前车架、后车架、驾驶室、发动机、自卸货箱等的形状设计与布置,关系到铰接式自卸车是否能够顺利实现转向的问题。轴距大,以上结构布置较容易,转向时不易发生干涉;轴距小,不仅要合理安排各部件、结构的布置空间,还要考虑是否能够实现预期的转向角度而不产生干涉[12]。将铰接式自卸车轴距按5%增大或减小,铰接点以及前、后簧载质量质心的位置与前、后轴长之比与轴距未变化前相同。经计算铰接式自卸车轴距对簧载质量的侧倾角速度变化基本无影响。当车辆的轴距发生变化时,后轴各状态变量响应曲线图略;轴距变化时各状态参量稳态值,如表5所示。
4.4 铰接点位置
假设铰接式自卸车轴距L=3.94m不变,L1=0.66m、0.86m、1.06m、1.26m、1.46m、1.66m、1.896m,则L2=3.28、3.0、2.88、2.68、2.48、2.28、2.08时,铰接式自卸车前簧载质量质心仍位于前轴上方,后簧载质量质心距铰接点距离与L2之比不变[13],铰接点位置变化时各状态参量稳态值,如表6所示。
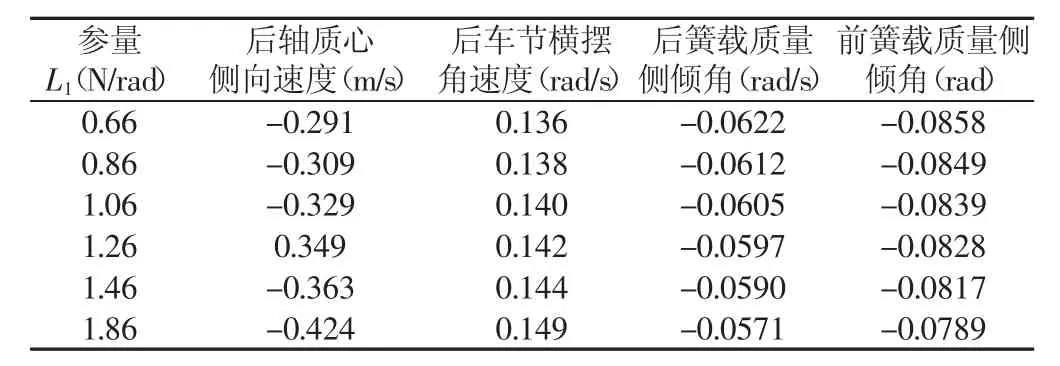
表6 铰接点位置变化时各状态参量的稳态值Tab.6 Steady-State Values of Various State Parameters
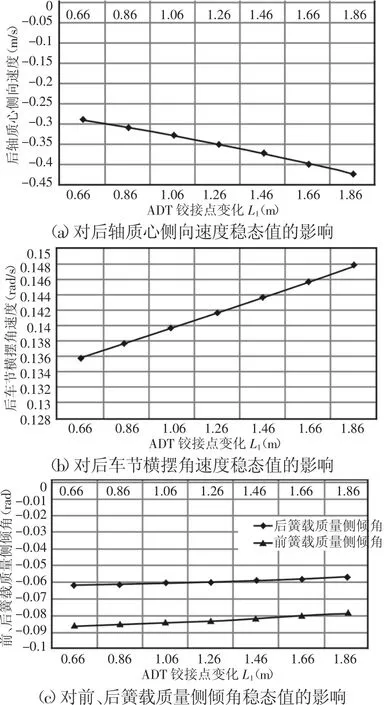
图2 铰接点位置的影响Fig.2 Effect of Hinge Point Position
由表6可知,铰接点越靠前,铰接式自卸车后轴质心侧向速度、后车节横摆角速度的稳态值越小,且后轴质心侧向速度稳态值随铰接点位置变化呈非线性变化,如图2(a)所示。后车节横摆角速度稳态值随铰接点位置变化呈线性变化,如图2(b)所示。但前、后簧载质量侧倾角的稳态值越大,为非线性变化,如图2(c)所示。前、后簧载质量侧倾速度摆动幅度也越大,后轴质心侧向速度、后车体的横摆角速度的反应时间和过渡时间则越短,但与之相反,簧载质量的侧倾角反应时间与过渡时间则越长。
5 结论
(1)前后悬架的弹簧有效距离、弹簧刚度、前后轴所载质量及前后轮胎侧偏刚度等是影响整车稳定性的重要参数;(2)当整车前轮胎的侧偏刚度取值越小时,对应后轮的取值在一定范围内增大,此种情况对整车操纵稳定性有利;(3)整车前后悬架的刚度对车辆质心处的侧向速度及横摆角速度影响较小;当车辆前悬参数取值越小而后悬取值越大,则稳态转向时,簧载质量的侧倾角取值减小;(4)轴距越靠前、铰接点越靠前布置越有利于提高操纵稳定性。
[1]Ko S Y,Ko J W,Lee S M.A Study on In-wheel Motor Control to Improve Vehicle Stability Using Human-in-the-Loop Simulation[J].Journal of Power Electronics,2013,13(4):536-545.
[2]Shiiba T C,Suda Y H.Development of driving simulator with full vehicle model of multibody dynamics[J].JSAE Review,2012,33(2):223-230.
[3]Rakheja S,Romero J A,Lozano A.Assessment of open-loop rollover control of articulated vehicles under different manoeuvres[J].International Journal of Heavy Vehicle Systems,2003,9(3):204-222.
[4]Solmaz S,Corless M,Shorten R.A methodology for the design of robust rollover prevention controllers for automotive vehicles:Part 1Differential braking[J].International Journal of Vehicle Autonomous Systems,2006,8(2/3/4):1739-1744.
[5]Huang H H,Yedavalli R K,Guenther D A.Active roll control for rollover prevention of heavy articulated vehicles with multiple-rollover-index minimisation[J].Vehicle System Dynamics,2011,50(3):1-23.
[6]姜右良,陈士安,何仁.新型铰接系统参数对BRT客车转向动态性能的影响[J].机械设计与制造,2013(10):163-166.(Jiang You-liang,Chen Shi-an,He Ren.Influences of New Articulation System Parameters on Steering Dynamic Characteristics of BRT Vehicle,2013(10):163-166.)
[7]申焱华,李艳红,金纯.电驱动铰接式工程车辆操纵稳定性控制分析[J].农业工程学报,2013,29(12):71-78.(Shen Yan-hua,Li Yan-hong,Jin Chun.Analysis of handling stability for electric-driven articulated truck[J].Transactions of the Chinese Society of Agricultural Engineering,2013,29(12):71-78.)
[8]张学艳,张文明,罗维东.六轮电驱动铰接式自卸车操纵稳定性研究[J].汽车工程,2014(11):1327-1333.(Zhang Xue-yan,Zhang Wen-ming,Luo Weidong.A Study on the Handling Stability of an Articulated Dump Truck with Six Motor-driven Wheels[J].Automotive Engineering,2014(11):1327-1333.)
[9]王锐,苏小平,王卫.汽车操纵稳定性中悬架特性分析与优化[J].机械设计与制造,2015(5):96-99.(Wang Rui,Su Xiao-ping,Wang Wei.Analysis and Optimization of Suspension Characteristics in Vehicle Handling Stability[J].Machinery Design&Manufacture,2015(5):96-99.)
[10]贾小平,樊石光,于魁龙.铰接车铰接点位置分析与计算[J].装甲兵工程学院学报,2014,28(2):36-39.(Jia Xiao-ping,Fan Shi-guang,Yu Kui-dou.Analysis and Calculation of Hinged Point Position for Articulated Vehicles[J].Journal of Academy of Armored Force Engineering,2014,28(2):36-39.)
[11]钟恒,陈树新.六轮电驱动铰接车行驶状态功率流试验[J].农业机械学报,2012,43(6):8-14.(Zhong Heng,Chen Shu-xin.Power Flow Experiment and Analysis of Driving States on Six-wheel Electric Drive Articulated Vehicle[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(6):8-14.)
[12]魏巍,刘昕晖,陈延礼.在复杂环境中2自由度轮式铰接车辆的越障能力[J].吉林大学学报:工学版,2011,41(5):1205-1209.(Wei Wei,Liu Xin-hui,Chen Yan-li.Obstacle surmounting capability of 2-DoFarticulatedvehicleinrough terrain[J].Journal of JilinUniversity:Engineering and Technology Edition,2011,41(5):1205-1209.)
[13]胡建军,刘辉,何铮斌.驱动力分配控制对车辆转向行驶稳定性的影响[J].中国公路学报,2013,26(5):183-190.(Hu Jian-jun,Liu Hui,He Zheng-bin.Influence of Driving Force Distribution Control on Vehicle Steering Stability[J].China Journal of Highway and Transport,2013,26(5):183-190.)
