塔式起重机刚柔耦合动力学模型研究
2018-01-19曹旭阳高顺德
杨 悦,曹旭阳,高顺德
(大连理工大学 机械工程学院,辽宁 大连 116024)
1 引言
塔式起重机系统是典型的欠驱动系统,而且重物的非线性运动又和臂架、塔身等具有大长细比的柔性构件的变形相互影响,增加了研究其动力学模型的难度。研究塔式起重机的动态响应对指导其结构的设计和提高安全性能具有重要意义,随着塔式起重机小车运行速度的提升和对重物移动位置精确性要求的提高,对其动力学特性进行研究的需求更加迫切。目前对塔式起重机的动力学特性研究主要将系统等效为多刚体系统,集中于重物摆动特性以及消摆控制方法的研究[1-4],而综合考虑塔式起重机结构特性对系统动力学响应的研究较少。文献[5]综合考虑了塔式起重机系统的刚度、阻尼、摩擦和空气阻尼等因素,将系统等效成了集中质量-弹簧系统,建立了数学模型并进行了实验,研究了回转运动产生的动载荷对系统的影响。文献[6]结合有限元方法和刚体运动学理论,研究了重物的摆动和系统的柔性对系统动力学响应的影响。文献[7]将塔式起重机等效为中心刚体-柔性臂模型,并用线性弹簧考虑拉杆对系统动力学响应的影响,应用Hamilton原理推导了描述系统回转和变幅运动的动力学控制方程。文献[8]将塔式起重机等效为平面柔性多体系统,综合考虑了臂架、塔身、平衡臂的柔性,仅针对回转制动工况进行了动力学分析。
综上,随着理论与技术的不断发展,国内外学者对塔式起重机的动力学特性研究越来越深入,但目前建立的动力学模型仍存在结构或运动描述不全面等问题,同时对理论模型的合理性的探讨也比较少见。基于此,重点研究在塔式起重机臂架的柔性变形和系统非线性运动的综合影响下,将臂架等效为Euler-Bernoulli梁并考虑臂架的自重和结构阻尼,应用拉格朗日方程和假设模态法建立完整描述塔式起重机变幅、回转和起升运动的离散化动力学方程。然后应用Maple数学软件对方程进行数值求解并与动力学仿真的结果进行对比。
2 运动学描述
2.1 变量定义
文献[7]主要考虑臂架的柔性和拉杆的影响,忽略塔身、平衡臂等结构的柔性,并且不考虑钢丝绳长的变化,建立的塔式起重机动力学模型,如图1所示。柔性臂架等效为Euler-Bernoulli梁,在水平面内回转。以臂架回转中心为原点,臂架的中线方向为X1轴建立固定坐标系O1X1Y1,作为系统输出参数的参照。O2X2Y2和O3X3Y3分别为固结在臂架根部和小车中心的浮动坐标系,用以定义臂架的变形和作大范围刚体运动的参数。对于细长梁,其纵向伸缩变形相对于竖直平面内的弯曲变形要小很多;且塔式起重机臂架水平面内的弯曲变形主要由惯性力引起,其相对于竖直平面内的弯曲变形也可忽略不计,故仅考虑臂架竖直平面内的弯曲变形,设其为w(x,t)。假设臂架初始时刻中线和X1轴重合,由静止开始进行回转、变幅、起升运动。忽略臂架变形对小车相对运动的影响,即假设小车始终沿着X2轴运动,在任意时刻t,描述系统的广义坐标为:小车相对于臂架根部的位移s(t),臂架相对于X1轴的回转角度α(t);钢丝绳相对于小车中心的长度l(t),重物在Z3Y3平面内的摆角和偏离平面的平面外摆角分别为 β(t)、γ(t);臂架在Z3X3平面内横向弯曲变形w(x,t)。为便于公式推导,上述广义坐标中,前3个广义坐标描述塔式起重机大范围刚体运动,将其作为系统输入量,记为向量 p=[x1,x2,x3]T;后 3个广义坐标为描述系统动力学响应的输出量,记为向量q=[x4,x5,x6(x,t)]T。xi(i=1,2…6)是关于时间的函数,记其关于时间的一阶、二阶导数分别为yi(i=1,2…6)、zi(i=1,2…6)。
2.2 构件坐标
臂架中线上任一点P1在浮动坐标系O2X2Y2下的坐标用向量表示为:R1=[x 0 x6(x,t)]T(1)
小车在臂架上运动,小车位置P2在浮动坐标系O2X2Y2下的坐标为:

重物位置P3在浮动坐标系O3X3Y3下坐标为:

设浮动坐标系O2X2Y2向惯性坐标系O1X1Y1转化的反对称
经过坐标变换,Pi(i=1,2,3)在惯性坐标系O1X1Y1的坐标用ri(i=1,2,3)表示为:

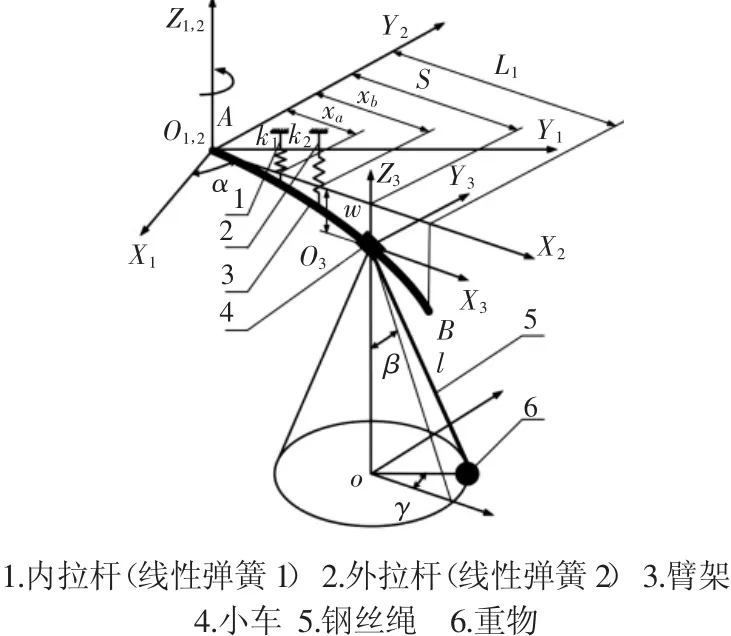
图1 塔式起重机动力学模型示意图Fig.1 Dynamic Model of a Tower Crane
2.3 构件速度将式(5)对时间求导,得各构件速度为:
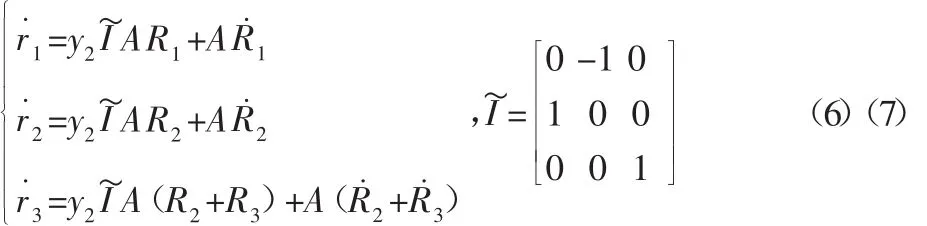
R˙i(i=1,2,3),Ri(i=1,2,3)表示对时间的一阶导数:
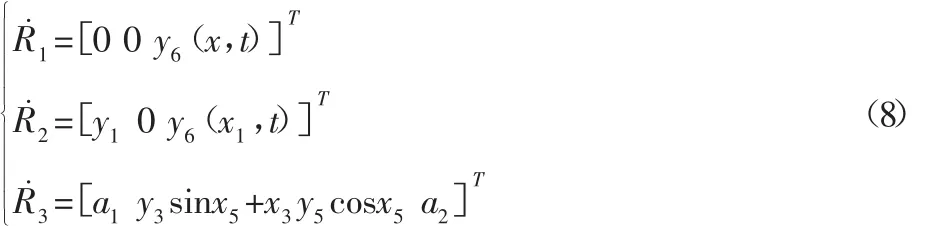
3 动力学方程推导及其离散
3.1 方程推导
使用拉格朗日方程来建立系统大范围运动规律已知的动力学方程[9],向量形式的拉格朗日方程的基本形式为:

式中:T—系统动能;V—系统势能;q—系统广义坐标向量;F—广
义力向量。对应于,上式的广义坐标向量为q=[x4x5x6]T,
F=0。系统的动能:
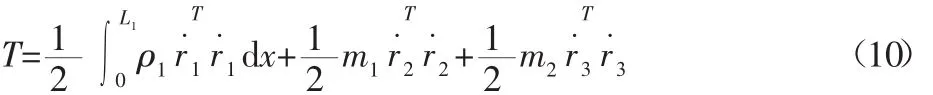
式中:等号右边第一项为臂架的动能,第二、三项分别为小车和重物
的动能;ρ1—臂架的等效线密度;L1—臂架的长度;m1、m2—小车和重物的质量。将式(6)代入上式便可得到系统的动能。
3.2 方程离散
采用假设模态法,将臂架任意点的横向弯曲变形表示为:

经过整理便可得到系统离散后矩阵形式的动力学方程:

式中:M、K—(2+n)×(2+n)维矩阵,分别是离散系统的广义质量矩阵和广义刚度矩阵;Q、G、Mi—(2+n)维列向量;Q—离散系统的输出广义坐标向量;Q¨—其对时间的二阶导数;G—包括离心力、科式力和重力在内的广义力向量;Mi—与输入广义坐标相关的广义质量向量。具体表达式为:

3.3 考虑结构阻尼的离散方程

式中:C—(2+n)×(2+n)维矩阵,为系统的结构阻尼矩阵;
Q˙—Q对时间的一阶导数,具体为:

考虑柔性梁的结构阻尼时,系统的动力学方程变为:
组合系数α和β计算公式为:
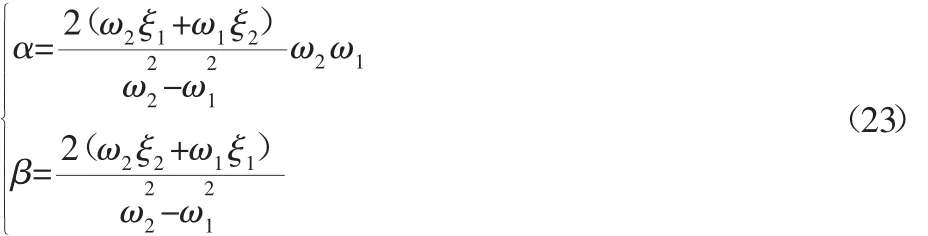
式中:ωi、ξi(i=1,2)—柔性梁的第一、第二阶振动频率和相应的阻尼比。
选取固定边界悬臂梁的模态函数,其元素为:
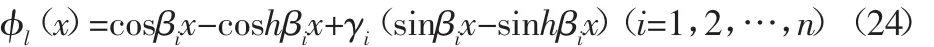
对应固定边界悬臂梁,其横向弯曲振动的固有频率计算式:
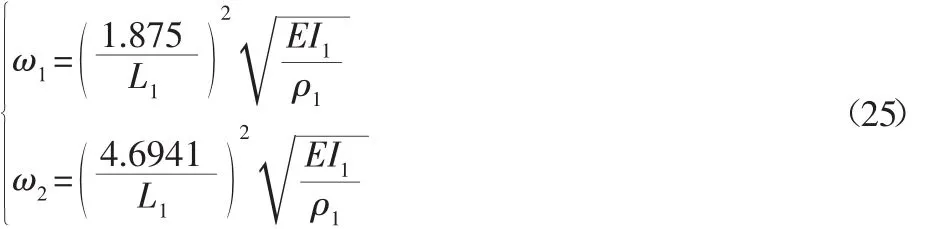
将式(21)~式(25)代入式(20)便可得到考虑结构阻尼的系统的离散动力学方程。
4 数值计算与动力学仿真
4.1 计算参数和仿真模型
上节推导得到了系统的离散动力学方程,首先使用Maple数学软件截取柔性梁的前二阶模态进行数值计算,然后与使用ADAMS进行动力学仿真的结果进行了对比。塔式起重机的系统参数,如表1所示。建立的塔式起重机ADAMS简化仿真动力学模型,如图2所示。模型中塔帽、臂架为柔性体,其余都为刚性体。
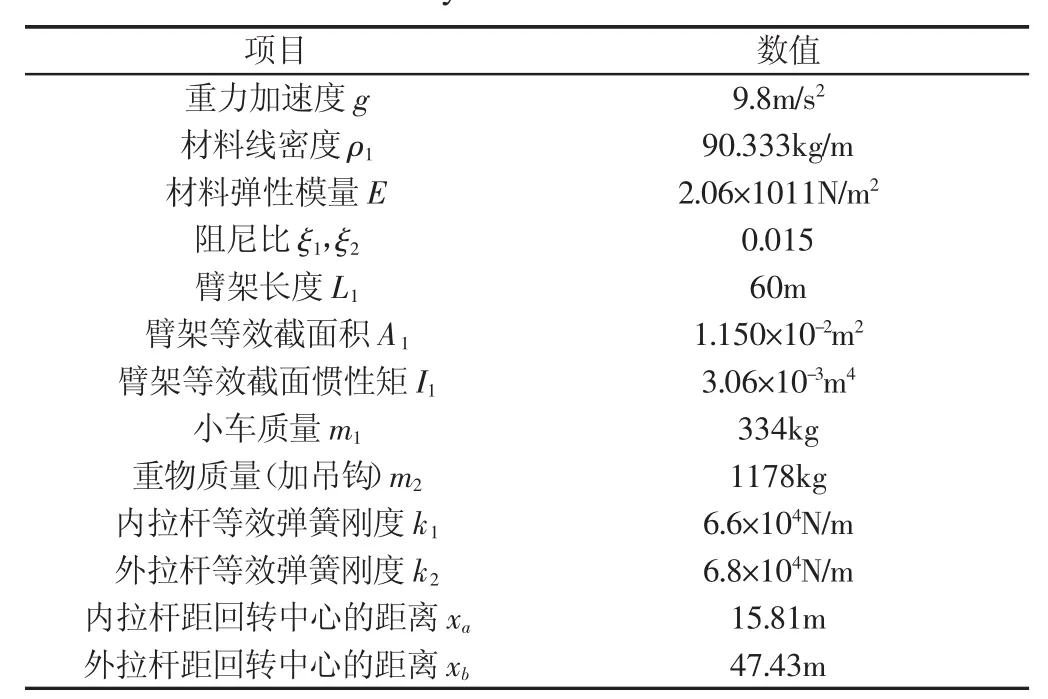
表1 系统参数表Tab.1 System Parameters
图2 塔式起重机ADAMS动力学模型Fig.2 ADAMS Simulation Model
数值计算和动力学仿真针对文献[10]中塔式起重机三种典型的运动形式,初始条件为小车距回转中心60m,钢丝绳长度为20m。第一种形式臂架进行先匀加速后匀速最后再匀减速的变幅运动,加速时间为0.5s,匀速运动10s,减速时间为0.5s,匀速运动速度为0.9m/s。第二种形式,臂架同时进行变幅和起升运动,运动时间为10.5s,且都为先匀加速运动再匀速运动,变幅加速时间0.5s,匀速运动速度0.9m/s,起升加速时间2.57s,匀速运动速度1.333m/s。第三种形式臂架进行先匀加速后匀速最后再匀减速的回转运动,加速时间为13.67s,匀速运动时间为10s,减速运动3.6s,匀速运动角速度为3.78°/s。各运动速度函数,如图3所示。
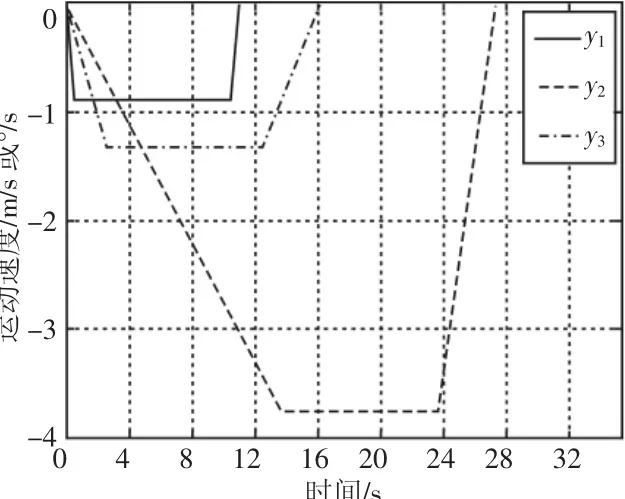
图3 变幅、回转和起升运动速度函数Fig.3 Velocities of Luffing,Rotating and Lifting Motion Respectively
4.2 仅变幅运动时结果对比
仅变幅运动时的计算和仿真结果,如图4所示。分析可知重物X方向位移的变化主要由变幅运动和重物的摆动产生,计算和仿真的结果基本一致,8s以后的差异主要是由于重物平面内摆角的差异造成。臂架竖直平面内的横向弯曲振动引起了重物Z方向位移的变化,由计算和仿真得到的其变化的幅值和周期基本一致。与数值计算结果比较,仿真得到的重物平面内摆角有周期性微幅的震荡,且变化周期更长,这一差异主要是因为数值计算中并未考虑臂架的轴向振动。
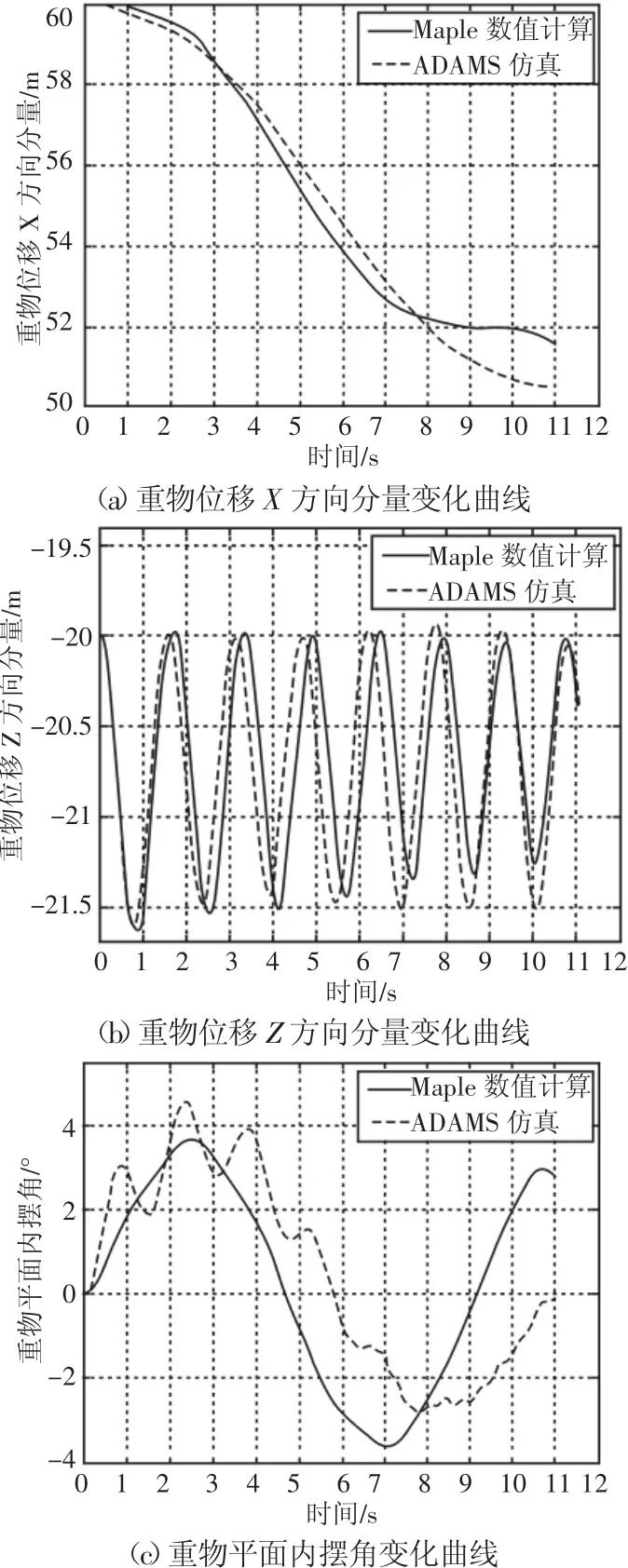
图4 仅变幅运动时重物运动响应曲线Fig.4 Dynamic Response of the Payload When Luffing Only
4.3 同时变幅和起升运动时结果对比
同时进行变幅和起升运动时的计算和仿真结果,图略。起升运动和臂架的横向弯曲振动引起重物Z方向位移的变化,变化的周期和臂架的振动周期一致。重物平面内摆角仍有微幅的震荡,且计算和仿真结果仍存在周期差异。另外,与第一种形式比较,起升运动引起了摆角幅值的增大和周期的缩短。
4.4 仅回转运动时结果对比
仅回转运动时的计算和仿真结果,图略。比较可知,计算和仿真得到的重物X方向和Y方向位移的变化趋势都几乎一致。Z方向位移的变化在初始阶段比较吻合,但随着时间的增加,计算的结果较仿真的结果其幅值变小而周期变长。另外,重物平面内的摆角和平面外的摆角的振动周期仍存在差异,且仿真得到的结果存在明显的周期性震荡,这种差异产生的主要原因仍然是由于计算过程中忽略了臂架的轴向振动和水平面内的横向弯曲振动。可知在回转减速运动阶段,重物平面外的摆角会迅速增大。
5 结论
(1)建立的动力学模型可以完整地描述塔式起重机各种典型的运动过程,较准确地跟踪重物运动过程的位移响应。(2)数值计算结果表明模型可以近似地反映重物平面内和平面外的摆角响应,动力学仿真结果还表明臂架的轴向振动和水平面内的横向弯曲振动会引起摆角的周期性微幅震荡。(3)变幅运动和回转运动都会引起重物平面内的摆动。回转运动还会引起重物平面外的摆动,当回转快速制动时会引起摆角的迅速增大。同时进行变幅和起升运动时,起升运动会引起重物摆动幅值的增大和周期的缩短。的研究结果对研究塔式起重机的动力学响应和跟踪重物轨迹、研究重物的摆动规律具有重要的指导意义,同时对于研究大长细比臂架类工作机构的动力学响应也具有重要的参考价值。
[1]TZU-SUNG W,MANSOUR K,WEN-SHYONG Y.Anti-sway tracking control of tower cranes with delayed uncertainty[J].Fuzzy SETS and Systems,2015,1(10):1-20.
[2]KOUMBOULIS F N,NIKOLAOS D K,GIANNARIS G L.Independent motion control of a tower crane through wireless sensor[J].ISA Transactions,2015(11):1-9.
[3]DAVID B,JASON L,JON D.Radial-motion assisted command shapers for nonlinear rotational slewing tower crane[J].Control Engineering Practice,2010(18):523-531.
[4]王宝家,殷晨波.塔机位置与防摆控制研究[J].机械设计与制造,2015(1):165-168.(Wang Bao-jia,Yin Chen-bo.Research of tower crane’s position and antiswing control[J].Machinery Design&Manufacture,2015(1):165-168.)
[5]JERMAN B,PODRZAJ P,KRAMAR J.An investigation of slewing-crane dynamics during slewing motion-development and verification of a mathematical model[J].International Journal of Mechanical Sciences,2004(46):729-750.
[6]JU F,CHOO Y S,CUI F S.Dynamic response of tower crane induced by the pendulum motion of the payload[J].International Journal of Solids and Structures,2006(43):376-389.
[7]YANG Wen-qing,ZHANG Zhi-yi,SHEN Rong-ying.Modeling of system dynamics of a slewing flexible beam with moving payload pendulum[J].Mechanics Research Communications,2007(34):260-266.
[8]兰朋,陆念力.塔式起重机柔性臂回转制动过程动力分析[J].哈尔滨工业大学学报,2004,36(5):677-680.(Lan Peng,Lu Nian-li.Dynamic analysis of flexible jib of tower crane in case of braking slewing motion[J].Journal of Harbin Institute of Technology,2004,36(5):677-680.)
[9]蔡国平,洪嘉振.旋转运动柔性梁的假设模态方法研究[J].力学学报,2005,37(1):48-56.(Cai Guo-ping,Hong Jia-zhen.Assumed mode method of a rotating flexible beam[J].ACTA Mechanica Sinica,2005,37(1):48-56.)
[10]吕玉兰.塔式起重机操作培训模拟系统的研究与实现[D].大连:大连理工大学,2015.(Lv Yu-lan.Research and implement of operation training simulation systemfortowercrane[D].Dalian:DalianUniversityofTechnology,2015.)
