铝多孔洞演变行为的分子动力模拟

方 洲，刘晓波，徐庆军

（南昌航空大学 航空制造工程学院，江西 南昌 330063）

1 引言

近五十年来，铝已成为世界上最为广泛应用的金属之一。但是，铝很容易受到温度，压力等因素的影响；同时在制造过程中，存在着不可避免的各种缺陷，如缩孔、砂眼、气孔、夹渣、微观裂纹、杂质、孔洞、刻痕、切口等，这些缺陷容易降低铝材的质量，并在宏观上影响成品力学性能，甚至导致材料断裂失效[1-2]。断裂失效造成的事故往往使生命和财产蒙受巨大的损失。我们常常看到的列车出轨、飞机失事、桥梁坍塌以及各种大小车祸等均是由材料缺陷演变的断裂失效所致[3]。因此，掌握金属内部的裂纹、孔洞等缺陷的演变规律，对于预防类似事故的发生具有重要的指导作用。

随着科学技术的快速发展，特别是计算机技术的发展，使需要大量计算的分子动力学方法得以兴起和广泛应用[4-8]。文献[9]对铝单晶中心贯穿微裂纹的愈合过程进行了分子动力学模拟。结果表明，当加热温度超过临界温度，或外加压应力Kl超过临界值时微裂纹将完全愈合。文献[10]利用嵌入原子模型方法在型加载情况下，研究单晶Ni在有缺陷和没有缺陷下的裂纹扩展情况。获得了裂纹尖端的临界负载和应变能的分布。分子动力学模拟根据原子间势函数不同的获取方法，又可以分为经典分子动力学和现代分子动力学。经典分子动力学是以牛顿力学为基础来计算原子间的相互作用，而现代分子动力学里的原子相互作用的计算是基于量子力学考虑了电子的影响。针对不同的研究对象和体系，两种方法各有优劣。总的来说，面对简单体系及金属材料时经典分子动力学模拟计算量更小同时与实验结果十分吻合，而面对复杂体系时，由于势函数获取更为准确故常采用现代分子动力学方法。分子动力学方法是对某一体系内某一时刻下所有已知位置和速度的粒子通过运动方程求解出粒子下一时刻的位置和速度的一种“确定性方法”，并由此推断出在当前条件下温度、压力、动能、势能等热力学性质。借助分子动力学模拟铝制品内部的裂纹、孔洞等的演变可以使我们深入的了解复杂的机制，对于预防类似事故的发生具有积极的指导作用。便是在原子尺度下使用经典分子动力学方法在分子动力学模拟软件LAMMPS（Large-scale Atomic/Molecular Massively Parallel Simulator）中，对含有预制微观孔洞的铝在受速度加载拉伸作用时的变形机理进行了研究。

2 计算模型

单晶铝的结构及物理特性，如表1所示。

表1 单晶Al结构及物理特性Tab.1 The Structure and Physical Properties of Al

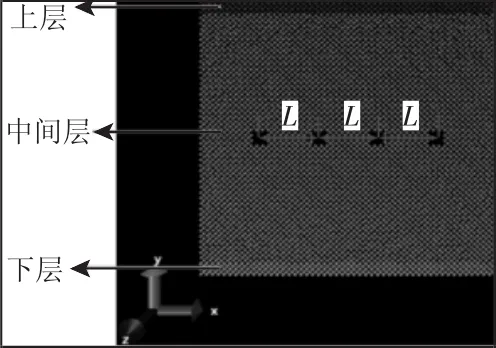
图1 预制等间距孔洞分子动力学初始模型Fig.1 Molecular Dynamics Initial Model with Prefabricate Equally Spaced Voids

在LAMMPS中根据表1数据建立模型，如图1所示。x、y、z方向的尺寸分别为50a0×50a0×0.25a0，a0为晶格系数，将原子模型分为三个区域：上层、中间层、下层，在XY平面上，上层和下层对应的区域大小为50a0×2a0，中间层的中间水平位置上预制4个相同大小的孔洞，孔洞为边长为2a0的正方形；同时4个孔洞的孔中心间距相同为L=10a0，对应的孔洞的坐标，如表2所示。将系统初始温度设为1K，低温可以避免原子的热激活效应。本模型采用嵌入原子法进行分子动力学模拟，X和Y方向采用非周期性边界条件，Z方向采用周期性边界条件。以时间步长为1fs对整个体系充分弛豫，达到平衡状态。根据本模型的大小，将中间层原子和上层原子在Y方向上的初始速度设定为0.35A°/ps，X和Z方向的初始速度设置为0，下层原子设置为固定不动。模拟的时间步长设定为0.001ps，整个体系采用微正则系综（NVE），整个程序运行60000步，每间隔一千步记录一次原子的坐标位置、动能、势能和总能量。

表2 图1模型中孔洞中心在x-y坐标Tab.2 The X-Y Coordinates of Voids in the Fig.1

3 模拟的势函数和算法

分子动力学的对象是一个粒子系统，系统中的原子间的相互作用用势函数来描述，因此采用EMA[11]势函数进行模拟，计算铝原子之间的相互作用，系统的总势能表示为：

式中：Fi—嵌入能函数；ρi—除了第i个原子以外所有原子在i处产生的电子云密度之和；φij—第i个原子与第j个原子之间的对势作用函数；rij—第i原子与第j个原子之间的距离。运用分子动力学方法计算有N个粒子系综的运动方程时，根据牛顿力学建立微分方程如下：

式中：mi—第i个原子的质量；ri—第i个原子的原子坐标；Fi—作用在第i个原子上的力；ai—第i个原子的加速度。

原子的初始位置以及初始速度为已知条件，利用微分方式（2），即可以求出任意时刻的原子位置和速度。再利用统计力学便可求解模型体系的平均动能和势能，而总能量为两者之和。

模拟使用Velocity-Verlet算法进行计算。其基本算法形式为：

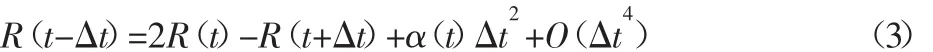
Velocity-Verlet是通过原子在t时刻的位置R（t），加速度a（t）及 t-Δt时刻的位置计算出t+Δt时刻的位置R（t+Δt）。

4 等间距的多孔洞体系演变行为的结果与分析

首先，对模型进行运算，运算完后对模拟结果采用可视化操作，以获得等间距孔洞的整个原子运动的轨迹图。提取了几个特殊时刻下体系等间距孔洞的原子图，如图2所示。

体系运行3000步时的原子图，如图2（a）所示。此时可以看到体系中编号2、3孔洞之间已经产生微裂纹缺陷，编号2、3孔洞内边缘已经开始产生微小的滑移以及微裂纹，但是孔洞的大小与初始模型相比没有明显的变化，其它区域的原子没有非常明显的变化。

图2 特殊时刻下的裂纹扩展原子图Fig.2 Under the Special Moment of Crack Extension Atomic Figure

12000步时的原子图，如图2（b）所示。图中可以很明显的看出，编号2、3孔洞的内边缘产生的裂纹的尖端原子出现了大面积的混乱排列，原子晶格位置发生重组；此时编号2、3孔洞之间的裂纹不断产生子裂纹，子裂纹继续扩展又产生新的子裂纹，由于编号2、3孔洞内边缘裂纹扩展产生的子裂纹在不断的接近，导致编号2、3孔洞之间区域被裂纹不断扩展，此时编号2、3孔洞已经快被裂纹贯穿。另外，编号1、2孔洞的内边缘开始发射位错、产生微小的滑移及微裂纹。

21000步时的原子图，如图2（c）所示。此时非常明显的变化是编号2、3孔洞已经被其内边缘裂纹扩展完全贯穿。同时随着编号2、3孔洞内边缘产生的裂纹进一步扩展，裂纹尖端变得更加钝化。上层与中间层的边缘产生了撕裂，编号1、2孔洞内边缘产生裂纹不断相互扩展使其间距越来越小；编号3、4孔洞也相同。其他区域没有明显的变化。

41000步时的原子图，如图2（d）所示。此时产生明显的变化是编号1与2、3与4孔洞由于内边缘裂纹扩展已经完全贯穿，此时编号1、2、3、4孔洞之间完全贯穿。另外体系的左右中间边缘已经开始产生滑移并进一步向内扩展，同时编号1、4孔洞内边缘产生的裂纹也进一步向外扩展，体系经过一系列的循环过程：母裂纹扩展—裂纹尖端钝化—母裂纹产生子裂纹—子裂纹尖端钝化—产生次子裂纹，最终加载体系被完全贯穿。

5 孔洞大小及孔间距对含多孔洞的铝演变行为的影响

5.1 孔洞大小对含多孔洞的铝演变行为的影响

为了探求孔洞的大小对体系的影响，在初始模型的基础上改变预制孔洞的大小，分别设置了孔洞边长均为0.5a0、1.5a0、2a0、2.5a0四种情况下体系运行的情况，将体系运行的结果绘制为时间步数—总能量曲线图，不同孔洞大小的体系总能量演变图，如图3所示。

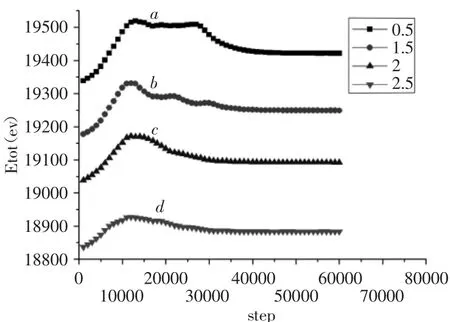
图3 不同孔洞大小的体系总能量演变图Fig.3 System Energy Evolution with Different Voids

间距相等、孔洞边长均为0.5a0的能量曲线，如图3（a）所示。能量曲线经历快速上升至最高点然后下降至一个平稳的位置保持了大致10000步的时间步长，然后能量又开始下降。直到大概44000步后，能量曲线保持在一个稳定水平至最后。

间距相等、孔洞边长均为1.5a0的能量曲线，如图3（b）所示。能量曲线大致经过12000步快速上升至最高点。然后能量曲线下降过程中又经历了两次轻微下降并且后两次的能量的下降都是先保持一定的时间步后才继续下降。最后随着体系继续下降，在40000步左右时体系被完全拉开，能量曲线保持在一个稳定水平至最后。

间距相等、孔洞边长均为2a0的能量曲线，如图3（c）所示。能量曲线先快速上升至最高点，此时时间步大致为12000步，然后随着体系进一步加载，能量曲线开始下降。对孔洞边长为2a0的能量曲线进行观察，我们发现曲线在下降区域内变化较为平缓，没有出现如孔边长为0.5a0、1.5a0曲线那样的平稳一段时间后再下降的情况。在时间步为37000步左右时体系被完全拉开，能量曲线保持在一个稳定水平至最后。

间距相等、孔洞边长均为2.5a0的能量曲线，如图3（d）所示。能量曲线同样是先快速上升至最高点，此时时间步约为12000步。然后随着体系进一步加载能量曲线开始下降，对比其他三个孔的曲线，发现孔边长为2.5a0的曲线的下降过程最为平缓。在体系加载到时间步为35000时体系被完全拉开，能能量曲线保持在一个稳定水平至最后。

综合分析图3不同孔洞大小的体系总能量演变图，不同的孔洞大小对应的能量曲线都是在12000步左右时体系能量达到相应的最高点。但是孔洞的边长越大，对应的孔洞的整体能量水平越低，能量曲线在下降的过程表现为越来越平稳没有波动。可以推断随着模型中4个等间距、等大小的孔洞边长变大，孔洞边缘发射的位错与相邻孔洞以及模型左右两侧边界发射的位错汇合的概率更大，所需的能量也越低，孔洞的演变路径在Y方向也更加规则，因此从孔洞到达最高点开始至体系完全被拉开的区间内能量曲线趋于平稳下降。最后，随着孔洞边长的增加，体系被拉开所用的时间步更少。

5.2 孔间距对含多孔洞的铝演变行为的影响

为了探究不同的孔间距对含预制孔洞的体系演变的影响，本节分别设置初始模型中的L为6a0、8a0、10a0对比在这三种孔洞等间距情况下体系的演变规律，其他条件与初始模型一致。得到能量曲线图，如图4所示。

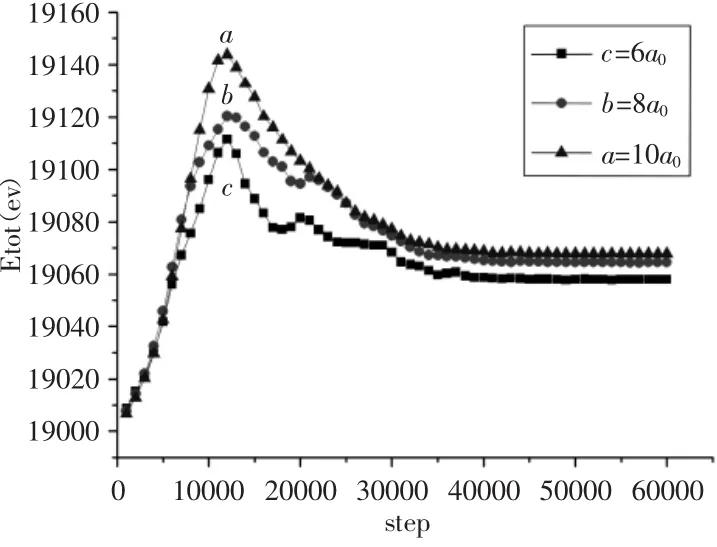
图4 不同孔间距下的能量演变图Fig.4 Energy Evolution Under Different Void Spacing

对于图4中曲线a：其先经历一个上升阶段在12000步左右时达到能量最高点，然后开始下降，直到40000步左右时体系被完全拉开，此后能量曲线处于一个稳定位置。对比b、c曲线，a曲线的最高点最高，下降的阶段是十分平稳没有明显的波动。

对于图4中曲线b：其先经历一个上升阶段在12000步左右时达到能量最高点，对比c曲线最高点，b曲线的最高点大于c曲线的最高点。随后曲线开始下降，直到40000步左右时体系被完全拉开，此后能量开始处于一个稳定的位置。但在它的下降阶段，曲线出现了一个波动后又继续平稳下降。

对于图4中曲线c：其先经历一个上升阶段在12000步左右时达到能量最高点，然后开始下降，直到40000步左右时体系被完全拉开，此后能量曲线处于一个稳定的位置。但在它的下降阶段，曲线出现了多个较大的能量波动并有短暂的稳定阶段。

综合分析曲线a、b、c；第一，它们都是在12000步左右时被加载到能量最高值，此刻模型中4个孔洞刚开始演变；但随着孔洞间距L的减小，a、b、c曲线的最高值依次减小。这是因为随着4个孔洞之间的三处间隔区域直线距离L减小，使得孔洞之间的区域整体原子结合力减小从而导致体系内孔洞（因为体系内含4个孔洞，各个孔洞开始演变的时间有间隔）开始演变所需要吸收的能量减小，即间距越大越难被拉开。第二，随着孔洞间距的减小，能量曲线在下降阶段的波动数量越来越多，幅度越来越大，变化趋于复杂。这是因为孔洞内边缘原子间结合力是非常弱的，所以导致孔洞的内边缘在孔洞刚开始演变时会出现很多微小位错以及微小裂纹，孔洞之间的间隔越近就越容易出现彼此内边缘发射的位错及产生的微裂纹相互汇集从而导致体系能量出现多个波动。

6 结论

建立含多孔洞的铝的分子动力学模拟模型，通过观察特殊时刻下的原子运动轨迹图，详细的说明了特殊时刻体系的裂纹扩展规律和孔洞的生成及汇集等情况，对于等间距的多孔洞铝的研究表明，随着孔洞直径的增大，其越容易与相邻的孔洞汇合，体系会更快、更容易被拉开。在孔洞尺寸相同的情况下，孔洞间距越大即体系内孔洞分布越均匀，孔洞开始演变所需要吸收的能量也越多，也就是含有均匀分布的孔洞的模型更难被拉开。这也表示集中分布的孔缺陷比均匀分布的孔缺陷危害更大。同时，相邻孔洞内边缘产生的微裂纹、发射的位错更容易因为间隔较大互相引导发展成为一条大的、规则裂纹，从而使体系被拉开时的演变十分平稳。

［1］卢功辉.金属型铝合金铸件裂纹产生原因及对策［J］.特种铸造及有色合金，2006，26（5）：308-310.（Lu Gong-hui.Metal type aluminum alloy casting crack causes and countermeasures［J］.Special Casting and Nonferrous Alloys，2006，26（5）：308-310.）

［2］陈明，李革，张文飞.纳米尺度孔洞周围应力集中现象分析［J］.材料导报 B：研究篇，2011，25（3）：131-134.（Chen Ming，Li Ge，Zhang Wen-fei.Discussion on the phenomenon of stress concentration around hole in nano-scale［J］.Material Review B：Research，2011，25（3）：131-134.）

［3］张俊善.材料强度学［M］.哈尔滨：哈尔滨工业大学出版社，2004：107-109.（Zhang Jun-shan.Strength of Engineering Materials［M］.Harbin：Harbin Institute of Technology Press，2004：107-109.）

［4］M.M aki-Jaskari，K.Kaski，A.Kuronen.Simulations of crack initiation in silicon［J］.Computational Materials Science，2000（17）：336-342.

［5］W.P.Wu，Z.Z.Yao.Molecular dynamics simulation of stress distribution andmicrostructureevolutionaheadofagrowingcrackinsinglecrystalnickel［J］.Theoretical and Applied Fracture Mechanics，2013（62）：67-75.

［6］Aude Simar，Hyon-Jee Lee Voigt，Brian D.Wirth.Molecular dynamics simulations of dislocation interaction with voids in nickel［J］.Computational Materials Science，2011（50）：1811-1817.

［7］刘晓波，徐庆军，刘剑.铝裂纹扩展行为的分子动力学模拟［J］.中国有色金属学报，2014，24（6）：1408-1413.（Liu Xiao-bo，Xu Qing-jun，Liu Jian.Molecular dynamics simulation of the aluminum crack propagation behavior［J］.Transactions of Nonferrous Metals Society of China，2014，24（6）：1408-1413.）

［8］余震，陈定方，朱宏辉.基于分子动力学的微纳米切削模拟研究进展［J］.机械设计与制造，2009（11）：217-219.（Yu Zhen，Chen Ding-fang，Zhu Hong-hui.Development of research in micro-nanometric cutting simulation based on molecular dynamics［J］.Machinery Design&Manufacture，2009（11）：217-219.）

［9］周国辉，高克玮，万发荣.微裂纹愈合过程的分子动力学模拟［J］.自然科学进展，2001（3）：300-305.（Zhou Guo-hui，Gao Ke-wei，Wan Fa-rong.Molecular dynamics simulation of micro crack healing process［J］.Progress in Natural Science，2001（3）：300-305）

［10］Majid Karimi，Tom Roarty，Theodore Kaplan.Molecular dynamics simulations of crack propagation in Ni with defects ［J］.Modelling Simul.Mater.Sci.Eng.，2006（14）：1409-1420.

［11］Ackland G J，Vitek V Many-body potentials and atom-scale relaxations innoble-metalalloys［J］.PhysicalReviewB，1990，41（15）：10324-10333.