运用R矩阵方法研究低能电子与NO2分子的散射∗

朱冰 冯灏

(西华大学理学院,成都 610039)

(2017年5月21日收到;2017年9月9日收到修改稿)

1 引 言

电子与分子散射在大气物理、天体物理、生物物理、等离子体物理等领域具有非常重要的应用价值,一直受到理论研究和实验工作者的关注[1−3].低能散射电子由于与束缚电子的能量相当,与靶分子之间存在复杂的相关/极化和交换作用,因此理论上精确研究低能电子和分子散射仍然存在较大的挑战.

二氧化氮(NO2)分子是一种具有刺激性气味的有毒气体,在空气中很容易转化为硝酸化合物,会对人体的呼吸系统造成极大的伤害.由于它可以与地表的臭氧发生发应,因此也被认为是大气污染的元凶之一[4,5].对中高能电子与NO2分子的散射已经有了广泛的研究,但是在低能领域的报道还较少.理论上,Munjal等[6]运用R矩阵方法研究了入射能量在12 eV以下的弹性散射截面.Curik等[7]在单中心展开法的基础上,采用可分离的交换势和模型相关/极化势,计算了20 eV以下的积分弹性散射截面.Gupta等[8]运用R矩阵方法结合球复式光学势计算了0.5–2000 eV的总截面.实验上,Szmytkowski等采用线性衰减方法测量了电子与NO2分子在0.6–220 eV的散射截面[9],并且用电子能谱仪测量了在3–370 eV范围内的积分截面[10].

在入射能量小于10 eV以下时,不同方法得到的散射截面存在较大差别.因此理论上采用严格的从头计算方法研究低能电子和NO2分子的弹性与非弹性散射截面,仍然具有重要的意义.本研究采用广泛使用的UK多原子R矩阵软件包[11],考虑静电-交换(static-exchange,SE)和密耦合(closecoupling,CC)两种模型,细致研究了入射能量小于10 eV时的弹性和非弹性散射截面,并对共振区域进行了分析.

2 理论方法

2.1 RRR矩阵

UKR矩阵方法是一种严格的从头计算散射方法,已广泛应用于低能电子与多原子分子的散射研究,其理论思想已有充分的论述[1,11−13].核心思想是将整个空间分成内层和外层两个区域.在内层区,由于散射电子和靶体系电子不可区分,关联效应和交换效应非常强.在外层区,散射电子距离靶体系较远,和束缚电子之间的交换和关联效应很小,可忽略不计,相当于运动在电子与靶体系形成的长程局域势场中.

在内层空间,整个散射体系的波函数由靶分子和散射电子共同组成,可以用组态相互作用表示为

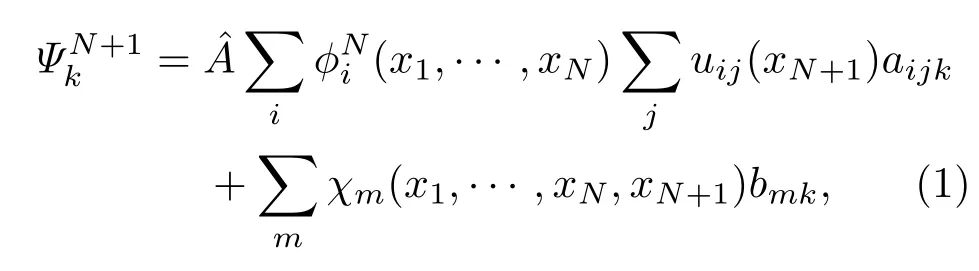
在本研究中,靶分子轨道分为冻结轨道、价键轨道和虚轨道,加上一组连续轨道来描述N电子体系和N+1电子体系.所有的轨道都采用高斯型基组,中心都取在分子质心.为充分考虑内层区域的关联和极化效应,本研究中R矩阵半径大小设为13 a0.

2.2 散射模型

研究中采用两种散射模型进行计算:SE模型和CC模型.对于SE模型,靶体系只有一种组态,因此束缚态电子不允许被散射电子极化,且未考虑关联效应.SE模型可以给出形状共振,但得到的共振能常常高于实验值.对于CC模型,可以包含更多的组态.在本研究中,将垂直激发能小于20 eV以内的所有电子组态(aug-cc-pVTZ基组下,共107个电子组态)都包含进来.这样,束缚电子在散射电子的作用下,能够激发到更高的活化空间,电子与电子之间的关联效应可以充分考虑.散射电子采用Faure等[14]的连续轨道,包含了直到g分波(l≤4)的贡献.为保证整个体系波函数的一致性,散射轨道在Schmidt和Löwdin对称正交化的作用下,与束缚态轨道正交[15].

2.3 靶分子

NO2分子是开壳层体系,属于C2v点群.其基态电子组态为:

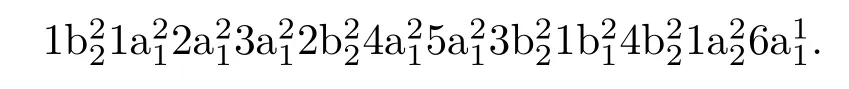
当只考虑SE模型时,采用限制性开壳层的Hartree-Fock(ROHF)波函数.当采用CC模型时,包含6个电子的最低三个占据轨道1b2,1a1,2a1被冻结,其余17个电子自由运动在活化空间中.为充分考虑关联效应,除了9个价键轨道外,给活化空间增加了2b1和7a1两个虚轨道.它们是能量最低的两个空轨道,其轨道能量分别为2.11和2.22 eV.UKR矩阵软件包在进行CAS-CI(complete-active-space con fi guration interaction)计算时,可以自动对电子组态的对称性进行分类.

为得到NO2分子的平衡结构,基于CFOUR程序[16],采用耦合簇单双激发加上微扰的方法(CCSD[T])进行优化.不同基组的优化结果列于表1中.

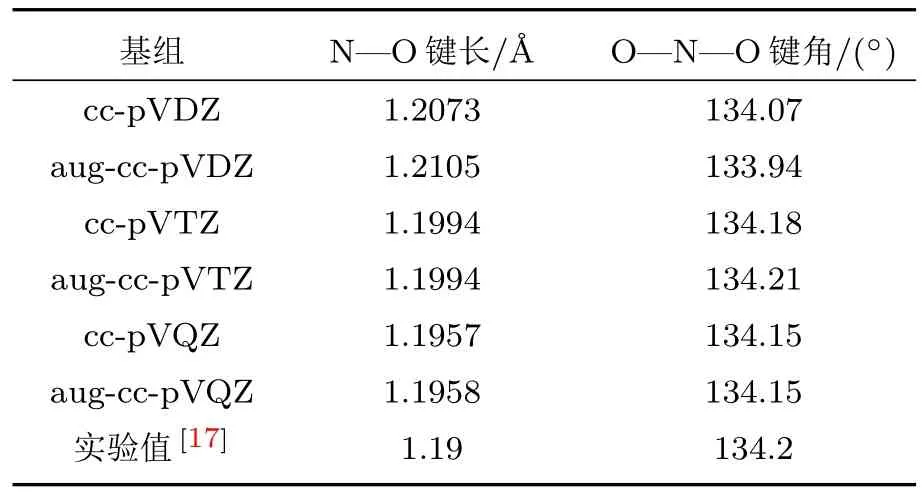
表1 NO2分子不同基组的优化结构Table 1.Optimized structures of NO2on different basis sets.

由于弥散函数影响散射电子与靶体系束缚电子的极化/关联作用,对于散射有比较重要的影响[18].且在不同基组的优化结果中,发现采用augcc-pVTZ基组的优化结果与实验值符合得很好.考虑计算量的大小和与实验值的比较,本研究采用aug-cc-pVTZ基组进行结构优化和散射计算.

NO2分子电子基态的SCF能量为−204.10 a.u.,CAS-CI能量为−204.16 a.u.,与Gupta等[8]的理论计算值−204.15 a.u.符合得很好.但我们得到的CAS-CI偶极距为0.41 Debye,比Cupta等[8]的计算值0.50 Debye低,更接近于 Leonardi等[19]的实验值0.316 Debye.所有的NO2分子参数列于表2,并与其他实验或理论结果进行了比较.

表2 e-NO2分子散射的靶体系性质Table 2.Target properties of e-NO2.

3 结果与讨论

基于SE模型和CC模型,计算了电子与NO2分子的总散射截面,图1给出了两种模型的截面比较.SE模型预测了两个共振峰:3B1对称性在1.85 eV(宽度为0.13 eV)附近的共振以及1B1对称性在3.27 eV(宽度为0.36 eV)附近的共振.CC模型不仅将这两个共振峰都向低能方向移动了,而且共振宽度也大大缩小.3B1对称性的共振峰移到了0.76 eV,宽度为0.054 eV;而1B1对称性的共振峰位置变成了1.82 eV,宽度为0.19 eV.这样,在2.0 eV附近的共振峰,应该来自于1B1对称性,而不是3B1对称性,这与Munjal等[6]的结论一致.Gupta等[8]预测这一共振峰的位置在大约3 eV附近,明显高于本文和Munjal等[6]的结果.

实际上,不同的基组也会影响共振峰的位置.在SE模型计算中,如果采用pVTZ基组,则3B1和1B1两个对称性的共振峰位置分别是1.93 eV和3.34 eV.可见,包含更多的极化和弥散函数,会降低共振峰的位置.

由于在SE模型中,靶分子只用一个组态描述,电子不能跃迁到更高的轨道,分子只能处于电子基态,因此该模型预测到的共振为形状共振.CC模型不仅能够预测形状共振,还可以预测到散射引起的靶分子激发到不同电子态而造成的Feshbash共振.结果显示1A1对称性在5.32 eV附近有一个共振峰,略低于Munjal等[6]的5.57 eV,而Gupta等[8]的6.7 eV共振峰位置高于本文和Munjal等[6]的结果.该对称性在8.50 eV还有一个小的共振峰,与Sotckdale等[21]的实验值符合得很好,Gupta等[8]也预测到了这个共振峰,但他们的预测位置为8.41 eV,略低于实验值.表3列出了本文计算的最低的几个共振峰位置和宽度.

图1 (网刊彩色)SE模型和CC模型下电子与NO2分子散射的总截面Fig.1.(color online)Total cross sections of electron impact on the NO2molecule based on SE and CC models.

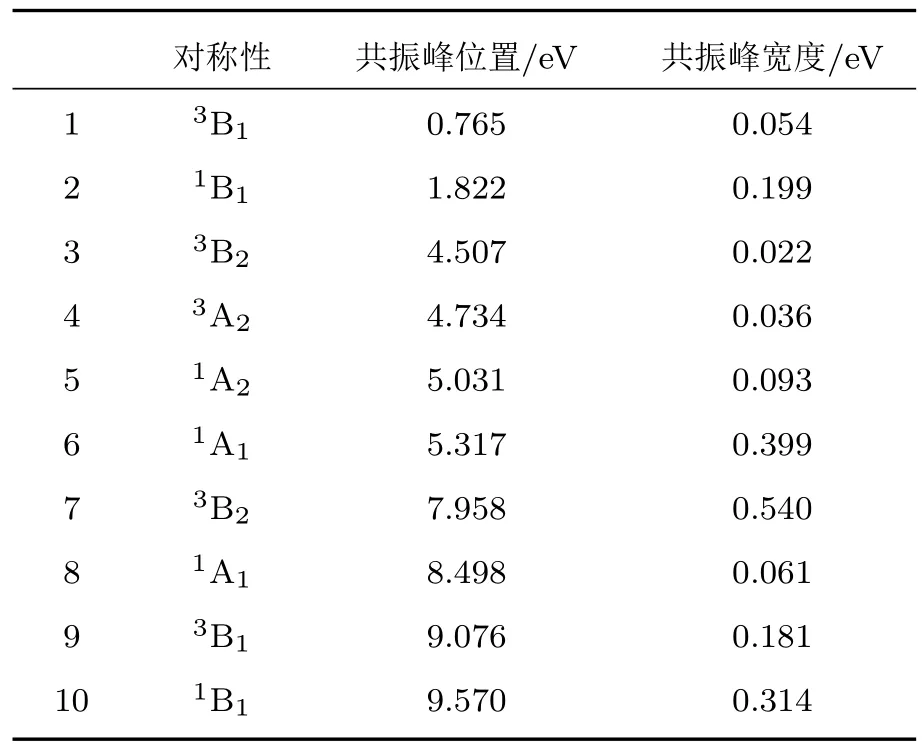
表3 e-NO2分子散射的共振峰位置和宽度Table 3.The positions and widths of resonances of e-NO2.

图2比较了本文计算的总截面与以前的理论和实验的结果.其中,Gupta等[8]同样采用R矩阵方法,但基于扩展的DZP基组和包含25个电子组态考虑关联效应.Curik等[7]对靶体系分别采用Hartree-Fock和密度泛函理论(DFT)两种轨道描述,运用单中心展开法结合模型极化势计算得到了低能的散射截面.由于NO2分子是极性分子,在极低能量(＜1 eV)时,截面会是发散的,本研究和以往的结果都显示了这一性质.

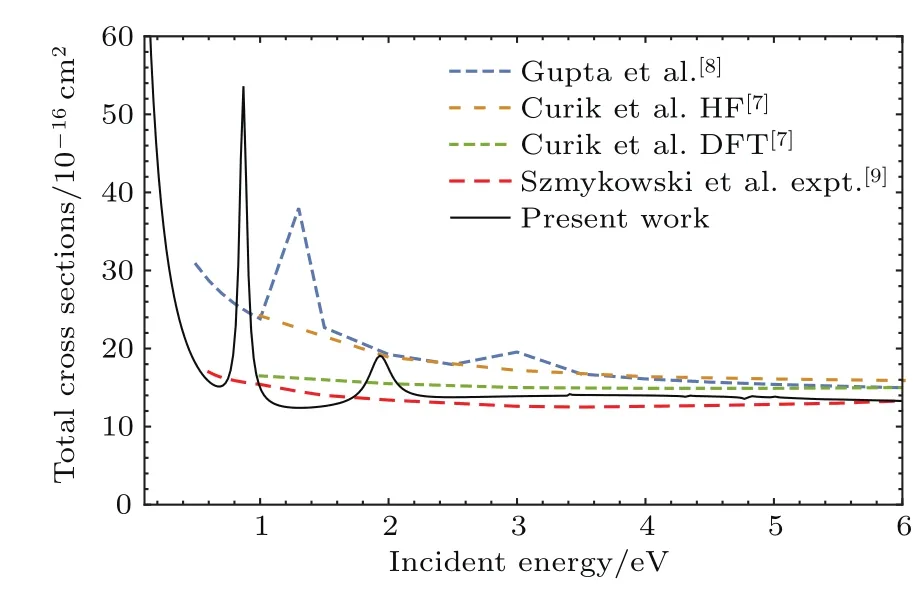
图2 (网刊彩色)电子与NO2分子散射的总截面Fig.2.(color online)Total cross section for e-NO2.

从图2可以看出,除了两个形状共振峰外,Gupta等[8]的理论计算结果和Curik等[7]采用Hartree-Fock轨道描述靶体系的结果非常接近.但是,当入射能量低于4 eV时,他们的计算结果都偏高于Szmykowski等[9]的实验测量值和本文的研究.并且,能量越低,偏差越大.Curik等[7]基于DFT轨道描述靶体系,可以较好地反映电子关联效应,与本文的研究一致,而且均与Szmykowski等[9]的实验结果符合得较好.但不论是Curik等[7]的理论研究还是 Szmykowski等[9]的实验测量,都没有发现入射能量小于4 eV时的两个共振峰.本文的研究发现在0.76 eV位置,有一个非常强的形状共振,低于Gupta等[8]的1.33 eV共振能.另外,在1.82 eV时,还存在一个较宽的形状共振,其位置仍然低于Gupta等[8]的3 eV共振能.这两个共振峰对应于O−的离解通道,已经被Rangwala等[22]的实验所证实.

为进一步探讨关联效应对于极低能量散射的影响,我们分别采用不同的基组和包含不同数目的靶体系电子态,进行CC散射计算,在图3中进行了比较.图3(a)是分别采用pVTZ和aug-cc-pVTZ基组,包含107个靶分子电子组态的积分散射截面.图3(b)是基于aug-cc-pVTZ基组,但分别包含21,82和107个靶分子电子组态的积分散射截面,包含82个电子组态和107个电子组态的截面已很接近,表明包含垂直激发能小于20 eV所有电子组态的CC计算,已经收敛.

上述两种方式都影响入射电子与靶体系束缚电子的极化/关联效应.可以看出,包含了弥散函数的基组,降低了入射能量小于4 eV时的散射截面;而包含更多的靶分子电子组态,不仅降低了极低能量时的散射截面,还降低了共振峰的位置.在这两种因素中,包含更多分子电子组态,能够更充分地考虑电子关联效应,这与束缚态的情形类似.

图3 (网刊彩色)关联效应对散射截面的影响 (a)不同基组;(b)不同靶分子电子组态数目Fig.3.(color online)In fl uences of correlations on total cross sections:(a)Basis sets;(b)target electronic states.

在图2中我们指出,Gupta等[8]的散射截面在极低能量处(＜4 eV)低于本文的理论值和Szmykowski等[9]的实验结果.从图3可见,Gupta等的结果和本文包含21个电子态的结果非常接近.实际上,Gupta等[8]和Munjal等[6]是分别采用25个和21个电子态,基于DZP基组进行CC研究的.因此,包含更多的靶体系电子组态进行CC计算得到收敛的截面,对于极低能量处的散射十分重要.

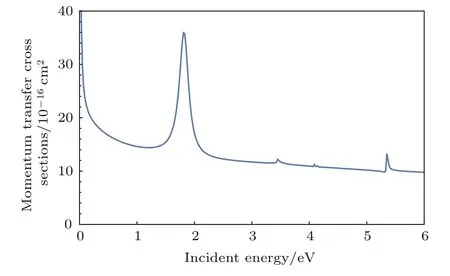
图4 电子与NO2分子散射的MTCSFig.4.MTCS for e-NO2.

最后,计算了低能电子与NO2分子散射的动量迁移截面(momentum transfer cross sections,MTCS).图4显示出MTCS具有明显的反向散射特性.由于共振的影响,MTCS在低能处也表现出波动性质.

4 结 论

NO2分子是大气中非常重要的一种自由基分子,能够加速臭氧层的破坏.低能电子与NO2分子的散射研究在理论和实验上仍然存在不一致性.本文采用R矩阵方法,基于aug-cc-pVTZ弥散基组,包含垂直激发能小于20 eV的所有靶体系电子组态,使用SE和CC两种模型,详细研究了入射能量小于10 eV时电子与NO2分子散射的积分截面和MTCS.结果表明,采用CC模型的R矩阵计算与实验符合得很好,而且可以预测低能散射的共振位置.

散射电子与束缚电子之间的关联效应对于低能散射是十分重要的.当采用弥散基组,包含更多的电子组态进行CC计算时,关联效应能够被充分考虑,散射截面在入射能量小于5 eV时有明显改善.

本研究得到的0.76 eV和1.82 eV两个形状共振峰位置偏低于以往的理论计算值,但本研究的积分截面值在低能处与实验结果符合得更好.建议今后理论和实验更关注电子和NO2分子在入射能量小于3 eV时的散射,尤其是共振区位置.

[1]Tennyson J 2010Phys.Rep.491 29

[2]Brunger M J,Buckman S J 2002Phys.Rep.357 215

[3]Winstead C,McKoy V 2000Adv.At.Mol.Phys.43 111

[4]Fuglestvedt J S,Isaksen I S A,Wang W C 1996Clim.Change34 405

[5]Abedi A,Cieman P,Coupier B,Gulejova B,Buchanan G A,Marston G,Mason G,Scheier P,Mark T D 2004J.Mass Spectrom.232 147

[6]Munjal H,Baluja K L,Tennyson J 2009Phys.Rev.A79 032712

[7]Curik R,Gianturco F A,Lucchese R R,Sanna N 2001J.Phys.B:At.Mol.Opt.Phys.34 59

[8]Gupta D,Naghma R,Vinodkumar M,Antony B 2013J.Ele.Spectrosc.Rel.Phen.191 71

[9]Szmytkowski C,Maciag K,Krzysztofowich A M 1992Chem.Phys.Lett.190 141

[10]Szmytkowski C,Mozejko P 2006Opt.Appl.36 543

[11]Carr J M,Galiatsatos P G,Gor fi nkiel J D,Harvey A G,Lysaght M A,Madden D,Masin Z,Plummer M,Tennyson J,Varambhia H N 2012Eur.Phys.J.D66 58

[12]Burke P G 2011R-Matrix Theory of Atomic Collisions:Application to Atomic,Molecular and Optical Processes(Berlin:Springer Press)

[13]Gillan C J,Tennyson J,Burke P G 1995Computational Methods for Electron-Molecule Collisions(New York:Plenum)

[14]Faure A,Gor fi nkiel J D,Morgan L A,Tennyson J 2002Comput.Phys.Commun.144 224

[15]Morgan L A,Tennyson J,Gillan C J 1998Comput.Phys.Commun.114 120

[16]CFOUR,version 2.0b,a Quantum Chemical Program Package,Stanton J F,Gauss J,et al.http://slater.chemie.uni-mainz.de/cfour/[2016-10-11]

[17]NIST ComputationalChemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101,Johnson III R D http://cccbdb.nist.gov/[2016-10-18]

[18]Fu J,Zhu B,Zhang Y,Feng H,Sun W 2014J.Phys.B:At.Mol.Opt.Phys.47 195203

[19]Leonardi E,Petrongolo C,Hirsch G,Buenker R J 1996J.Chem.Phys.105 9051

[20]Lievin J,Delon A,Jost R 1998J.Chem.Phys.108 8931

[21]Stockdale J A D,Compton R N,Hurst G S,Reinhardt P W 1969J.Chem.Phys.50 2176

[22]Rangwala S A,Krishnakumar E,Kumar S V K 2003Phys.Rev.A68 052710