MoS2电子屏蔽长度和等离激元∗

2018-01-18陶泽华董海明

物理学报 2017年24期

陶泽华董海明

(中国矿业大学物理科学与技术学院,徐州 221116)

(2017年7月8日收到;2017年9月7日收到修改稿)

1 引言

电子元激发即等离激元是系统中电子集体振荡的能量,具有优越的介电性质和光电性质.早在20世纪初期,美国研究学者Wood等[1]观测到在金属质光栅中,会发生电磁波反常衍射的现象,此为最早发现的集体激发现象.1957年,美国的Richie[2]采用箔作为金属薄膜,应用快电子能量损耗方法初次确切证明了等离激元的存在.此后,Stem和Farrell[3],Otto[4],Kretschmann[5]及Raether[6]也陆续发展和扩展了等离激元科学的研究,并取得了一系列重要的研究进展.此外,被调制的表面等离激元能够产生非常优异的光电特性,例如显著的选择性光吸收与散射特性[7]、局域电场增强特性[8]和突破光的衍射极限[9]、反常的介电特性[10]等性质.这些性质使得等离激元能够在超分辨率纳米光刻、光信息处理技术、超分辨率成像技术等领域发挥重要作用.随着对等离激元光子学研究的一步步深入,等离子光谱逐渐展现出它在光电子器件应用领域的巨大潜力,具有广阔的发展前景.

2004年,Novoselov和Geim首先剥离出单层碳原子层结构——石墨烯[12].石墨烯具有优越的物理性质,如超高的电导率和良好的热传导性能,在电子结构理论、量子霍尔效应和自旋电子学等诸多方面具有重要的研究和应用价值,两人因此获得了2010年诺贝尔物理学奖.虽然石墨烯性能非常优秀,但是它是无带隙的狄拉克系统,这使得石墨烯并不能提供较低的截止态电流,不能满足现代电子电路应用中的需求.由于二维材料在平面间虽然具有较强的化学键,但由于其相邻两层的耦合作用比较弱小,易于被分割成一个个互相独立的单层材料.因此,科学家考虑剥离出其他的具有直接带隙的二维材料,如单层二硫化钼(MoS2).在过渡金属层状二硫族化合物中,二硫化钼是间接带隙半导体材料,能带间隙约为1.8 eV,而其切割为单层时具有直接带隙,单层二硫化钼的直接带隙约为1.66 eV,从而弥补了石墨烯的不足,同时又具有良好的光学、电学、光催化等性能.早在1986年,研究者就通过插入锂的方法成功剥离出单层二硫化钼.最近也有报道称通过溶剂或裂解,可制备出单层MoS2.作为典型的类石墨烯单层二硫族化合物,单层二硫化钼由于优越的性质,在光学、电学和新能源材料等领域具有很好的应用前景.另外较石墨烯而言,它在光电子器件方面也具有更为广泛的应用领域,如电子探针、晶体管制造等.利用单原子层二硫化钼材料能够制造出高电流开关比和较高电子迁移率的低能耗场效应管,此项技术非常有希望用于下一代纳米电子器件和设备领域,将比传统的硅材料或石墨烯更有优势[11].

同时,MoS2也具有非常重要的光学性质.南洋理工大学的Yin等[13]发现单层MoS2比石墨烯拥有更优秀的光电响应特性,未来能够利用MoS2制作光电晶体管等新型光电器件.Mak等[14]发现单层二维的MoS2具有强的光发射效率,是普通块体材料的104倍.Lee等[15]研究了一、二、三层的MoS2纳米光子晶体管,发现三层的MoS2对红光的探测能力较强,两层和一层对绿光有较强的探测能力.与WS2,WSe2,MoSe2和TiS2等类似,MoS2是一种典型的层状过渡金属硫族化合物.量子限制会影响电子结构和光学性质,这些已经在MoS2的薄层和纳米管上被观测到.北京大学冯济研究员和王恩哥教授与中国科学院物理研究所和半导体研究所合作首次从理论上预言,并从实验上证实了单层二硫化钼的谷选择圆偏振光吸收性质[16],这表明二硫化钼在新奇量子特性的探索中具有重要研究价值.单层MoS2晶体为直接带隙半导体,具有强的光致发光效应,研究结果表明在MoS2这样的分层的d型电子结构中量子限制效应非常明显,也为在纳米级制造新型光电器件提供了可能.通过新型低维物理上的探索,d型电子之间的相互作用可以产生新的物理现象.量子限制效应会影响电子结构和光学性质,这已经在MoS2的薄层、纳米片和纳米管上被观测到.最近,北京大学物理学院和新加坡南洋理工大学的科研人员研究了单层MoS2的等离激元以及等离激元与激子的相互作用,研究发现自旋-轨道耦合对等离激元以及激子发光具有重要的作用,并且可以增强该系统的光致发光(PL)[17].中山大学的Yang课题组[18]研究了不同层数的MoS2等离激元对PL的影响,发现等离激元的能量转移可以导致材料PL的增强或淬灭.实验研究发现,通过改变MoS2的掺杂浓度,可以有效调控该系统的等离激元的共振,为MoS2在等离激元技术的应用指明了方向[19].材料的电子结构决定了材料的电子性质及其应用,而电子系统的多体效应,电子间的屏蔽效应和电子元激发-等离激元是电子系统最基本性质的体现,反映了电子系统最基本的结构和性质.为了更好地理解和研究单层二硫化钼系统电子结构和性质,发展以此为基础的光电器件,本文研究了单层二硫化钼电子多体效应、电子间的库仑屏蔽以及电子元激发.

2 理论模型

层状结构MoS2是钼和硫由共价键结合在一起的六方晶系结构,每一个晶体有很多硫和钼原子组成,当连接分子层之间的键被切断时,体材料的二硫化钼便被切割成单层二硫化钼.单层的二硫化钼是由三层原子层构成,其中上下两层为硫原子组成的六角平面,中间一层为钼原子层,将两个硫原子层隔开,从而形成了三明治夹心结构[20].层之内的每个钼原子被六个硫原子所包围,它们通过共价键结合,形成三棱柱状配位结构,六个硫原子分布在三棱柱体的各顶端,每个硫原子通过共价键和三个钼原子形成三棱锥型配位结构,钼原子位于单层二硫化钼的边缘位置,它和四个硫原子相互结合,而每个硫原子和两个钼原子结合.多层或体状的二硫化钼是由这些单层结构之间通过相对较弱的范德瓦耳斯力作用而成.因此,二硫化钼层与层之间相互作用较弱,但层内作用力却很强.这种特殊结构使得二硫化钼用作催化剂和润滑剂时的性能非常优越,利用微机械剥离法也较容易获得单层的高质量的二硫化钼样品.

2.1 单层二硫化钼的本征能量和波函数

为了研究该系统的电子性质,考虑单层的MoS2系统,该单层的电子系统置于x-y平面.在低能量区,可以通过如下的有效哈密顿量描述该区域电子的运动,即[21]

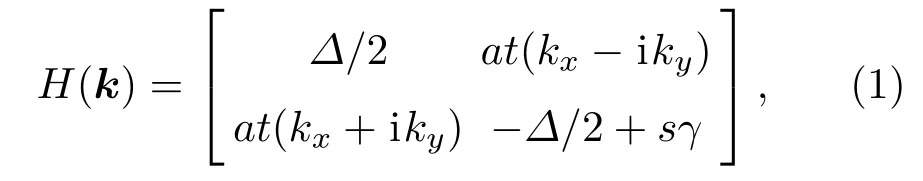
其中,k=(kx,ky)是电子波矢(动量算符),s=±1表示自旋向上和向下,晶格常数a=3.193 Å,最近邻原子之间电子的跳跃能t=1.1 eV.考虑自旋-轨道耦合,其耦合强度γ=75 meV,Δ=1.66 eV是禁带宽度[22].由该有效哈密顿量,求解该能量区的电子的薛定谔方程,即

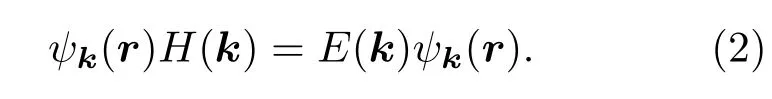
通过解析,可以得到单层二硫化钼电子的本征能量,即

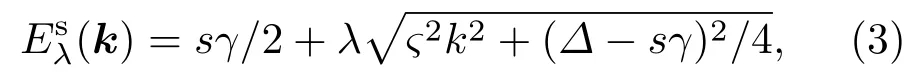
其中,λ=+1表示导带,λ=−1表示价带,ς=at,以及电子波函数,即

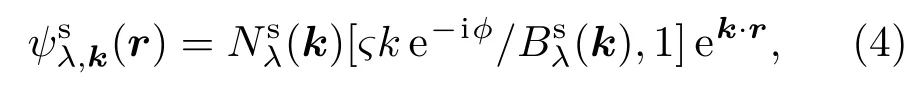
2.2 单层二硫化钼动态介电函数矩阵

通过电子波函数,以此可以计算单层MoS2电子系统的裸的电子-电子相互作用,该相互作用可以通过费曼图表示(如图1(a))[23],表达式可以写为

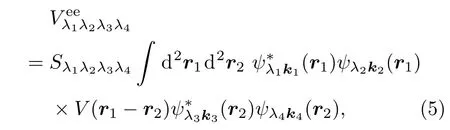
其中V(r)=e2/ε∞|r|是电子库仑相互作用势能,ε∞是材料的高频介电常数,Sλ1λ2λ3λ4=−i(λ1+λ2+λ3+λ4)/2=±1或者±i是由不同能带的电子的状态决定的符号函数.通过费曼图技术(如图1所示),电子在不同状态间的散射过程保持动量守恒,由此在动量空间,裸的电子-电子相互作用可以写成

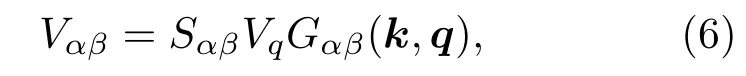
这里,α=(λ′λ)表示电子不同的跃迁过程,λ′=λ表示带内的散射跃迁,λ′/=λ表示带间的跃迁,q是电子散射过程中动量的变化,Vq=2πe2/ε∞q是二维情况下的库仑相互作用势的傅里叶变换系数.另外,

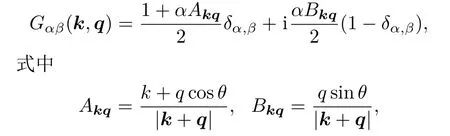
θ是电子动量k和q之间的夹角.

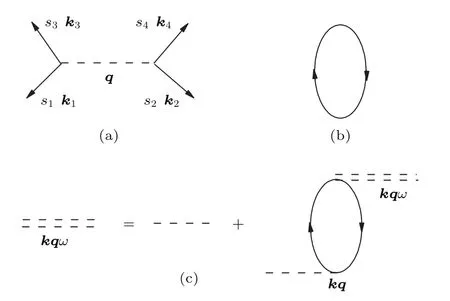
图1 (a)裸的电子-电子相互作用;(b)密度-密度关联函数;(c)无规相近似(PRA)下的电子-电子有效相互作用Fig.1.Electron many body Feynman diagrams:(a)Bare electron-electron interactions;(b)pair bubble;(c)effective electron-electron interactions.

通过格林函数和费曼图形自洽理论(如图1),有效的电子-电子多体相互作用可以表示为如下形式:

这里εαβ(ω,q)=δα,βδ(k)−VαβΠβ(k,q;ω)就是动态介电函数矩阵元,

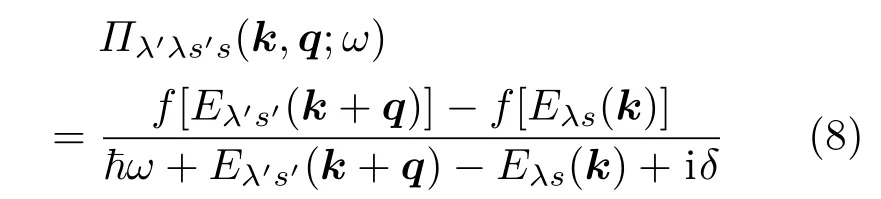
是密度-密度关联函数,在费曼图中可以由pair bubble图表示,如图1(b)所示.fλ(x)表示λ带的电子狄拉克-费米分布函数.ω对应电子元激发的频率,δ→0.另外,如果自旋和能谷是简并的,还需要考虑两者的简并.对于弱相互作用电子系统,在PRA下,电子-电子之间的有效相互作用可以如图1(c)进行展开. 令j=(λ′λ)=1=(++),2=(+−),3=(−+),4=(−−),并对k求和,从而得到动态介电函数矩阵

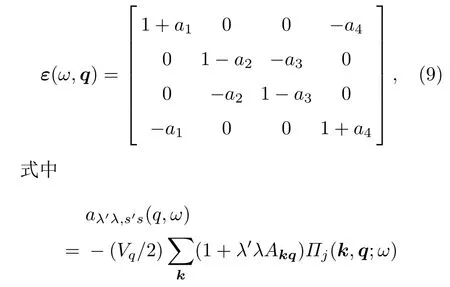
表示不同的电子元激发通道.当λ′λ,s′s取不同的值(±1)时,表示电子不同的激发通道.

2.3 态密度和电子间屏蔽效应

单粒子的自由格林函数为

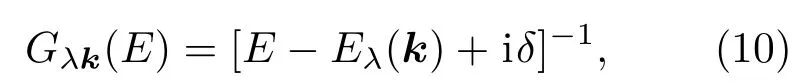
其中E是载流子的能量.通过该格林函数的虚部,可以计算得到系统载流子的态密度,即

很明显,由于自旋-轨道相互作用,导致态密度发生分裂.

在半导体研究中,载流子之间的库仑相互作用对半导体材料的物理性质有重要的影响,例如能带重整化、光吸收增强等效应.在低温情况(温度T→0)下,研究低温时的材料的光电输运性质时,必须考虑电流子之间的屏蔽效应[24].在研究载流子间的屏蔽效应时,一种比较粗糙的模型是费米-托马斯模型,而较为准确的模型是RPA模型.因此,本文利用RPA,当ω→0时,MoS2的静态介电函数的实部可以写为

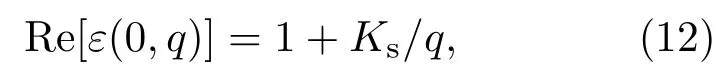
其中,Ks即为载流子之间的屏蔽长度,反映了载流子之间由于库仑作用导致的屏蔽效应.MoS2材料的载流子之间的屏蔽长度为

考虑n型掺杂的MoS2样品,即载流子为电子,则电子间的屏蔽长度为

其中,ν=(Δ−sγ)/at,η=4kq/(k2+ν2).K(x)和Π(n,x)分别是第一类和第三类完全椭圆积分.考虑到即使是高浓度重掺杂的样品,系统的费米能量EF依然远远小于带隙宽度Δ,并且能带接近抛物线形,当温度较低(T→0)时,可以分析得到MoS2导带中自旋向上s=+1(向下s=−1)的子带中电子之间的屏蔽长度

其中,kF是MoS2电子的费米波矢,ne是导带中电子的密度.上面的推导可以看出,MoS2电子间的库仑屏蔽效应依赖于其禁带宽度和自旋-轨道耦合,并且与一般的系统相比,其屏蔽效应要强得多,说明电子间的相互作用对其电子输运和光学性质都有重要影响.

2.4 单层二硫化钼集体激发

由于库仑作用的长程性和价电子易动巡游性,外部的微小扰动必然导致电子集体的振荡,即电子的集体元激发——等离激元.根据微扰理论,当没有外部作用施加于相互作用的单层二硫化钼电子系统时,即时,介电函数的响应方程Vαβεαβ(ω,q)−1→0,其中Vαβ存在非零解对应着系统的元激发,因此需要满足εαβ(ω,q)=0.由动态介电函数矩阵可以得出

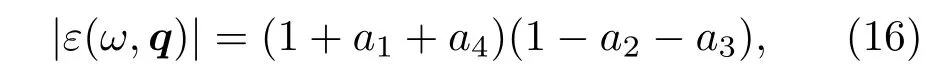
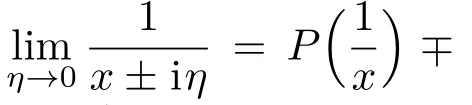
由于朗道阻尼作用,电子系统的电子元激发会退变成电子-空穴对的个别激发,从而导致元激发不能稳定存在.一般情况下,当元激发的波矢q较大时,元激发会退变成电子-空穴对的个别激发.受阻尼的元激发无法通过实验观察到.另外,价带中的电子,由于能量较小,被原子核束缚,会受到强的朗道阻尼,不能跃迁产生电子集体的元激发[25].因此,导带中的电子在较小的q区域 (q→0),即λ=λ′=+,可以产生稳定的电子元激发——等离激元.同时,为了研究电子多体相互作用的影响,考虑温度T→0时的情况.对于N型掺杂的MoS2系统,动态介电函数为1+a++=0.因此可由如下公式计算导带中电子的元激发,即

代入相应的表达式,将求和变成积分,方程(17)变为

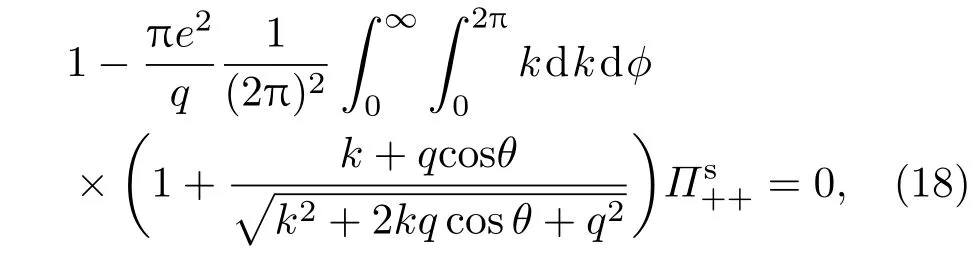
其中,ϕ是k与x轴的夹角,−E+s(k−q)]−1−[ħω+E+s′(k+q)−E+s(k)]−1.

在q→0的近似下,即对方程中的q进行泰勒展开,求解方程(18),可以计算得到导带中的电子元激发谱,即

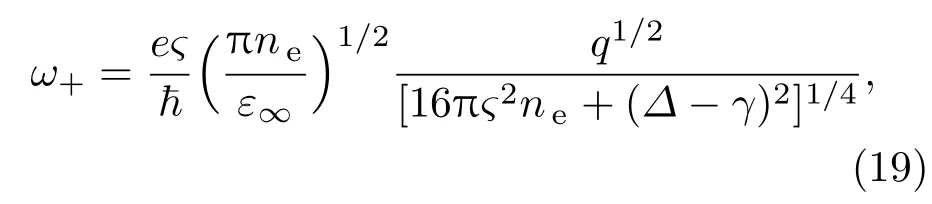
该等离激元是由导带中自旋向上(s′=s=+1)的子带中的电子集体激发产生的,ne是导带中的电子的密度.

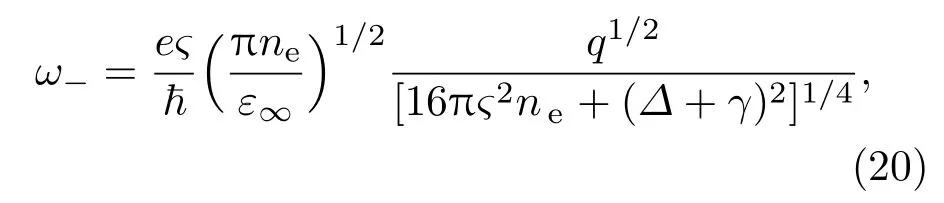
该等离激元是由导带中自旋向下(s′=s=−1)的子带中的电子集体激发产生的.另外计算显示,没有自旋极化的情况下,不存在导带中不同自旋子带间(s/=s′)的电子元激发.

3 结果分析

根据(14)式,图2计算了不同电子密度情况下,T→0时,电子屏蔽长度Ks随散射角度的变化.计算时忽略了不同电子自旋的影响,因为自旋-轨道耦合影响了屏蔽长度的大小,而对散射角度和电子密度的依赖行为是一致的.由计算可知,单层MoS2系统电子屏蔽效应较强.随着散射角度θ变大,屏蔽长度变小.这说明散射角度越大,电子间的屏蔽效应越小.当散射角度θ=0时,散射时电子的屏蔽效应最大.计算还表明电子密度越大,电子间的屏蔽长度Ks越大,即屏蔽效应越强.这是由于电子密度越大,整个电子系统就会越拥挤,从而使得电子间感受到更强的屏蔽效应.

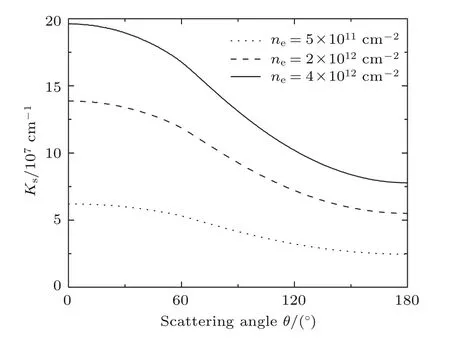
图2 不同电子密度时,电子屏蔽长度Ks随散射角度的变化Fig.2.The inverse screening length Ksas a function of scattering angle θ.

图3给出了导带中自旋向上的子带中的电子集体激发产生的等离激元谱ω+.由(19)式以及图3可以看出,该元激发ω+是声学型的,ω+∼q1/2,元激发的频率(能量)非常强地依赖于波矢q.随着电子密度的增加,其激发频率ω+明显增加.由此,可以通过改变单层二硫化钼系统的电子掺杂密度,有效地调节系统的电子元激发频率ω+.图4给出了导带中自旋向下的子带内的电子集体激发产生的等离激元谱ω−,由图4和(20)式可知,该激发谱ω−的性质与自旋向上的子带中的电子等离子激发光谱产生的等离激元谱ω+的性质相似,该元激发ω−也是声学型的,ω−∼q1/2,元激发的频率 (能量)非常强地依赖于波矢q.随着电子密度的增加,其激发频率ω−明显地增加.由此,可以通过改变单层二硫化钼系统的电子掺杂密度,有效地调节系统的电子元激发频率ω−.两个自旋子带的电子密度相同时,然而由于存在自旋-轨道耦合,这两支激发谱ω+∼(Δ−γ)−1/2和ω−∼(Δ+γ)−1/2仍然是不同的,很明显ω+＞ω−.由于γ=75 meV,考虑到γ≪Δ,可以得出说明随着q的增大或者电子浓度ne的减小,两个等离激元的频率的差别将变大.因此这种差异将在低能量区或低频率时(如太赫兹)表现得更加明显.通过调节电子密度,从而调节系统的电子元激发频率,可以方便地通过调控系统的电子密度,得到两支频率完全不同的等离激元激发ω+和ω−,得到双色的元激发.该研究结果能够很好地说明最近的实验研究发现,通过调控掺杂的电子浓度,调节系统的等离激元,从而调控材料的发光性能[19].

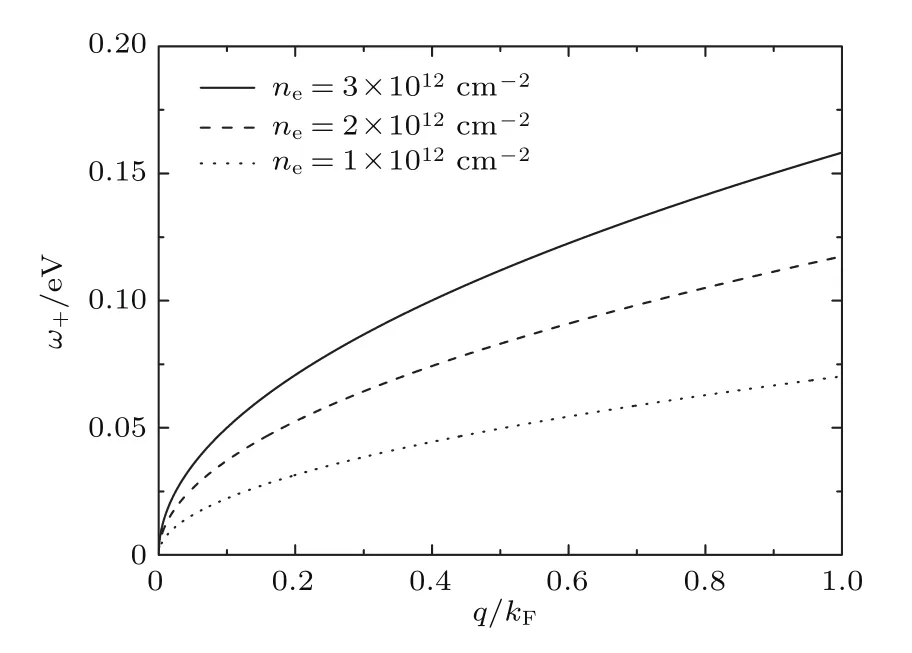
图3 不同电子密度时,自旋向上的子带中的电子元激发谱ω+(kF表示导带中电子费米波矢)Fig.3.Plasmon dispersion ω+in spin s=+1 subbands for different electron densities.

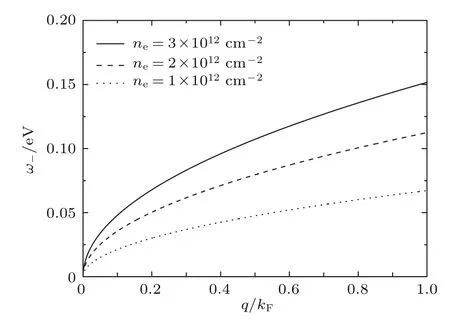
图4 不同电子密度时自旋向下的子带中的电子元激发谱ω−Fig.4.Plasmon dispersion ω− in spin s= −1 sub-bands for different electron densities.

传统的二维电子气的等离激元频率ωp=(2πe2nq/m∗)1/2∼q1/2∼n1/2[26],其中n为电子密度,m∗为电子有效质量;二维狄拉克系统石墨烯的等离激元频率n1/4[25],其中EF是电子的费米能量.二维单层MoS2系统的电子等离激元ω±∼q1/2.通过比较可以看出,这三种系统的元激发频率对波矢q的依赖关系都是相同的.但是,由于这三个系统能带结构非常不同,这三个系统的等离激元谱又有明显的不同,尤其是对电子密度的依赖关系不同.传统的二维电子气的能带是抛物线型的,其ωp∼n1/2;石墨烯是线性色散的能谱,ω′p∼n1/4;而单层的MoS2系统的能谱介于两者之间,是准线性的,元激发的频率ω±对电子密度的关系较为复杂.二硫化钼系统存在明显的自旋劈裂,自旋-轨道耦合作用扮演非常重要的角色,因此其存在两支等离激元模,并且其频率还依赖于禁带宽度Δ和自旋-轨道耦合γ,与其他系统有明显的不同.由此可见,自旋-轨道耦合对单层二硫化钼的能带结构和电子性质有重要的影响,该理论发现与最近的实验研究结果是一致的[17,18].

4 结论

考虑自旋-轨道耦合效应,研究了单层二硫化钼低能量区的电子结构和性质.自旋-轨道耦合对单层二硫化钼的能带结构和电子性质有重要的影响.MoS2的电子态密度和电子间的库仑屏蔽效应依赖于其禁带宽度和自旋-轨道耦合,并且与一般的系统相比,其屏蔽效应要强,说明电子间的相互作用对其电子输运和光学性质都有重要影响.通过费曼图形自洽方法,研究了该系统的电子元激发.研究发现,由于自旋的劈裂(能带的分裂),导致存在两支频率不同的自旋带内的等离激元激发,激发频率都正比于q1/2,并且随着电子浓度的增加激发频率增大.单层二硫化钼电子系统的电子性质非常不同于传统的二维电子气和石墨烯系统的电子性质.研究发现通过调控二硫化钼系统的电子浓度可以有效调节该系统两支等离激元的频率.研究结果显示单层二硫化钼材料是发展等离激元器件的理想材料.

[1]Wood R W 1902Phil.Magm.4 396

[2]Richie R H 1957Phys.Rev.106 874

[3]Stem E A,Ferrell R A 1960Phys.Rev.120 130

[4]Otto A 1968Eur.Phys.J.A216 398

[5]Kretchmann E 1971Eur.Phys.J.A241 313

[6]Raether H 1988Springer Tracts in Modern Physics111 110

[7]Khlebtsov B N 2008Phys.Rev.B77 035440

[8]Kahraman M,Tokman N,Culha M 2008ChemPhys Chem9 902

[9]Ruan Z,Qiu M 2006Phys.Rev.Lett.96 233901

[10]Smith D R,Padilla W J,Vier D C 2000Phys.Rev.Lett.84 4184

[11]Radisavljevic B,Radenovic A,Brivio J,Giacometti V,Kis A 2011Nat.Nanotechnol.6 147

[12]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004Science306 666