基于改进加权一阶局域法的空中交通流量预测模型

王 超，朱 明，赵元棣

(中国民航大学空中交通管理学院，天津300300)

空中交通流量时间序列的实时预测有助于掌握交通流的发展演化趋势和规律，为空中交通管理部门提供控制决策依据.作为空中交通流量管理和空域规划研究的重要前提和基础［1-2］，空中交通流量预测一直是国内外空管研究的热点之一.

当前空中交通流量预测方法主要分4类:(1)基于飞行计划的确定型流量预测方法，包括基于飞行计划4D轨迹预测方法［3］;(2)基于数理统计的预测方法，包括时间序列法、回归分析法、卡尔曼滤波法和指数平滑法等［1-2］;(3)非线性预测方法，包括小波分析预测法、混沌理论预测法和突变理论预测法等［4-5］;(4)智能预测方法，包括神经网络法、支持向量机等［5-6］.

由于空中交通以航班飞行任务计划为驱动，基于飞行计划轨迹预测方法首先发展起来.该方法以航空固定电报中的领航计划为基础，以航班动态报和雷达航迹为修正，建立航班4D轨迹推测模型，统计得到各空域单元的交通流量.然而，由于空中交通系统是一个多角色交互耦合的复杂非线性系统［7］，存在许多不确定性因素，航班实际运行4D轨迹与飞行计划轨迹经常存在较大差异，导致基于报文的流量预测精度较差.

为弥补上述不足，在国内外学者对空中交通系统非线性特性初步探索基础上，基于混沌时间序列方法的短期交通流量预测方法逐渐发展起来.Packard［8］提出重构相空间理论，开启了混沌时间序列的研究，此后混沌时间序列的全域法、局域法、基于最大Lyapunov指数［9］等预测方法相继出现.Cong等［10］利用关联维数和最大Lyapunov指数对空域扇区内交通流的混沌特性进行研究;Li等［11］利用最大Lyapunov指数对飞行冲突时间序列的混沌特性进行分析，证明了应用混沌理论进行飞行冲突预测的可行性;王超等［12］证明了交汇航路空中交通流具有混沌特性.上述研究成果为基于混沌理论的时间序列预测法应用于空中交通流量预测提供了理论基础，但并未将其应用于实际的交通流量预测中.因此，本文对基于混沌时间序列的预测方法进行改进并构建空中交通流量预测模型是非常有意义的.

加权一阶局域预测方法比神经网络法、基于最大Lyapunov指数预测法等具有待求参数少、快速等优点，能满足空中交通流量预测实时性强、操作简单、易实现等要求.吕金虎等［9］提出了加权一阶局域预测方法并将其应用到电力系统短期负荷预测中，但预测准确性还有很大的提升空间.空中交通流量控制和管理决策需要更高精度的流量预测，本文对加权一阶局域法的预测模型进行改进，并采用基于误差序列的误差修正方法对预测误差进行修正.最后，以北京区域管制中心某扇区交通流实测数据开展验证实验，先利用关联维数对空中交通流量时间序列进行混沌特性识别，之后分别用改进前、后的预测方法进行预测效果比对.

1 改进的加权一阶局域预测法

1.1 加权一阶局域预测法

对于混沌时间序列 x1，x2，…，xN，其中，N 为时间序列的长度，选取适当的嵌入维数m和时间延迟τ，进行相空间重构［13-15］，得到相空间为 Xi=(xi，xi+τ，…，xi+(m－1)τ)，i=1，2，…，M，其中 M=N－(m－1)τ.以预测中心相点XM作为参考相点，求参考相点 XM与前 M－1个相点的欧氏距离dl(l=1，2，…，M－1)，取与参考相点 XM的欧氏距离最小的m+1个相点，记为 XMn(n=1，2，…，m+1)，且对应的与参考相点XM的距离为dn，则相点XMn的权值为

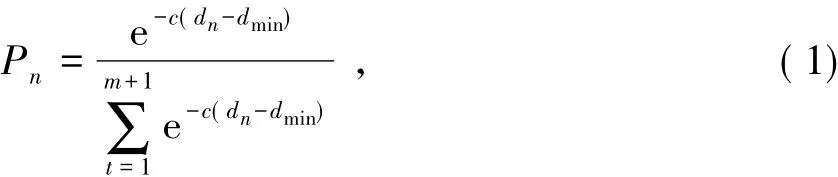
式中:dmin为dn中的最小值;c为参数，一般取c=1.

设参考相点XM的邻近相点集为{XMn}，其演化一步后的相点集为{XMn+1}.利用一阶局域线性拟合得到XMn和XMn+1的关系如式(2).

式中:E=(1，1，…，1)T为 m×1阶矩阵;a、b为拟合所需的实系数.

根据加权最小二乘法有

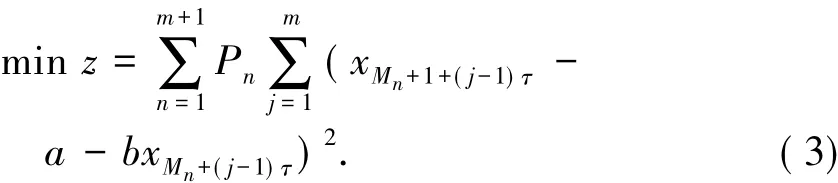
将式(3)看成是关于未知数a和b的二元函数，为求得使函数达到最小的未知数的解，求偏导并令其为0，可得

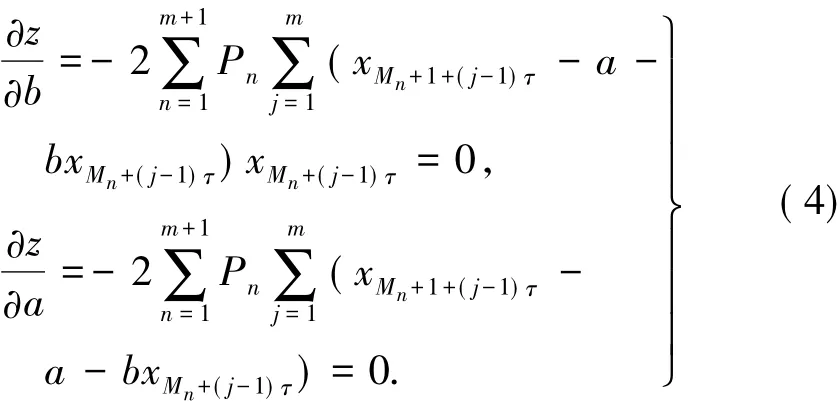
化简得

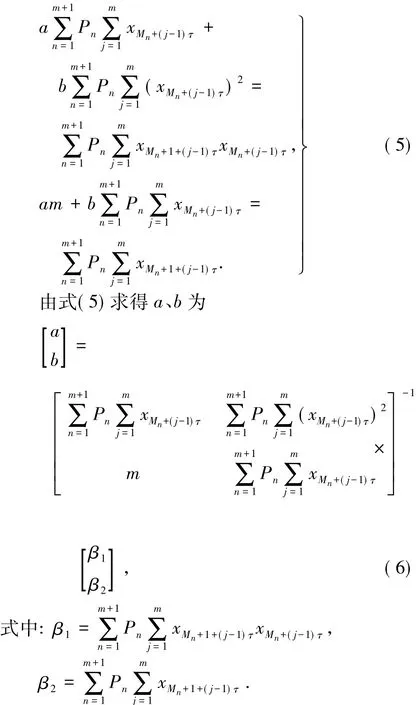
将求得的参数a、b代入式(7)，即可得到演化一步后的相点预测值X^M+1，如式(8).

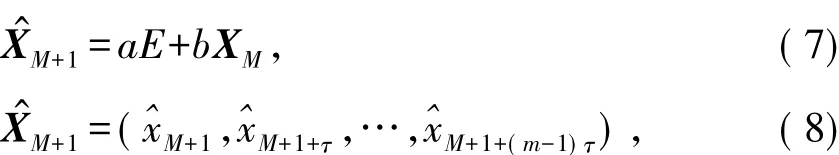
1.2 预测模型的改进

1.1 节所描述的未改进的加权一阶局域预测方法，是m+1个邻近相点XMn与其一步演化后的相点XMn+1的一阶局域线性关系参数a、b，作为相点XM与其一步演化相点XMn+1的一阶局域线性关系参数代入式(8)进行预测，即认为邻近相点的一步演化规律和参考相点一步演化规律相似.但实际上，由于用于预测的历史数据有限或出现特殊值等因素影响，邻近相点的一步演化规律并不能完全真实地反映出相点XM与其演化一步后的相点XM+1之间的关系.此外，邻近点的选取标准和选取个数等也会极大影响邻近相点的一步演化规律是否能更加真实地反映出参考相点的一步演化规律.因此，原有预测方法难免会存在偏差，这就降低了预测性能.

为克服上述缺陷，减小预测误差，考虑利用权值Pn对各邻近相点的演化规律进行加权，从而准确反映出预测相点的演化规律，以邻近相点的一步演化相点的规律来预测参考相点的一步演化相点，即以m+1个相点XMn+1的各分量加权和作为预测相点XM+1的各分量值，改进了预测式(7)，具体说明如下:

设m+1个最邻近相点的表达式为XMn=(xMn，xMn+τ，…，xMn+(m－1)τ).由式(1)求出 m+1 个最邻近相点对应的权值Pn，再依据式(5)、(6)求出预测参数 a、b，则预测公式为

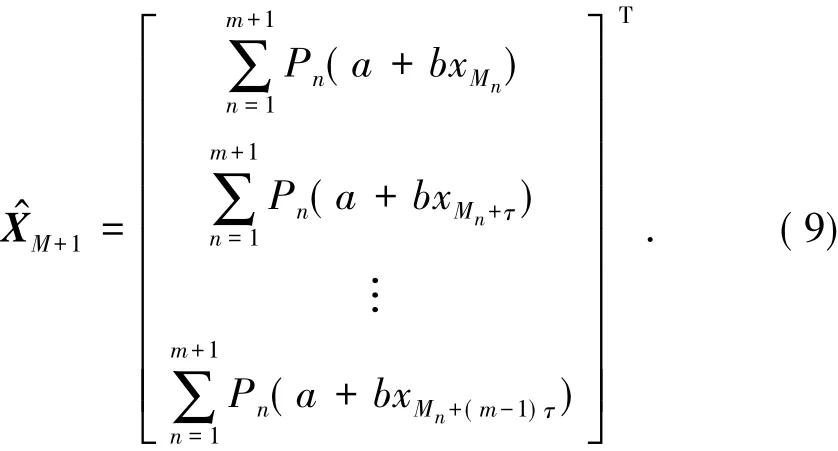
1.3 基于误差序列的预测误差修正

在加权一阶局域预测法的预测过程中，由前一步预测所得预测值代入原时间序列后求得下一步预测值.因此，如果不对每一步的预测值进行误差修正，存在误差的预测值将会直接影响下一步预测值的精度，这样逐步累积就会产生较大的累积误差，影响整体的预测准确性.为减小误差累计，本文采用基于误差序列的误差修正方法来进一步修正预测误差.

2 预测步骤

步骤1 对交通流量时间序列进行混沌特性识别，确定其延迟时间τ和嵌入维数m后进行相空间重构.

步骤2 当前状态相点XM为初始条件利用加权一阶局域预测法进行预测得到预测值^xN+1.

步骤3 利用基于误差序列的修正方法对预测值^xN+1进行误差修正.

步骤4 将修正后的预测值^xN+1代入原时间序列，对未来值^xN+2再进行预测，以此类推不断迭代进行多步预测.

3 空中交通流量预测实例及分析

选择北京区域管制某扇区2016年01月06日00∶00—24∶00之间扇区的空中交通流量作为预测实例.扇区空中交通流量是指按照一定的时间间隔来统计在此时间范围内扇区容纳航空器的数量.其中，统计时间间隔也称为时间尺度或时间序列标度，记为Δt.Δt的不同将直接影响交通流时间序列的形态特征，进而影响时间序列对系统特性的表达［12］.

为验证改进预测法对按不同Δt产生的交通流量时间序列均适用，本文拟选取4组不同Δt的时间序列进行验证实验.将以一天前20 h交通流量预测后4 h为例开展研究.统计时间间隔太大会遮蔽在此时间范围内流量动态变化特征，所以选择Δt=5，7，10，15 min，生成交通流量时间序列来验证本文预测方法是否对各时间尺度的交通流量时间序列均适用.图1给出了各时间尺度的交通流量时间序列示意图.

采用自相关函数法来计算时间延迟 τ［16-17］，自相关函数C(τ)=1－1/e时可以得到系统的最佳嵌入维数.

以Δt=10 min的时间序列为例，如图2所示，计算得到该时间序列的时间延迟τ=3.

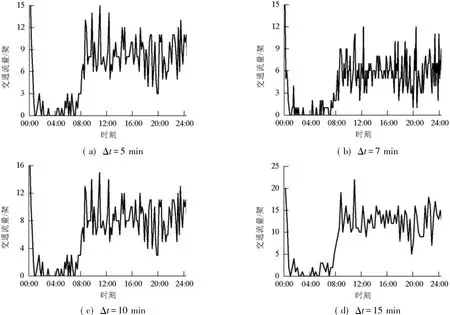
图1 不同时间尺度的交通流量时间序列Fig.1 Traffic flow time series at different time scales

3.1 基于关联维数的混沌特性判别

应用分形理论中关联维数的概念来判断时间序列是否具有混沌特性［10-12］.分维从测度理论和对称理论角度刻画了系统的无序性和复杂性，其中关联维数D2(m)是目前应用最广的分维数［18-19］.对于混沌系统，D2(m)会随着嵌入维数的增加而出现饱和现象，即不再随m的变化而变化［19］.关联维数就是关联指数随嵌入维数增大到饱和状态时的值，其值是对相空间中吸引子复杂度的度量.当D2(m)不是整数或者大于2时，系统表现出一种对初始条件敏感的混沌振荡.因此，对于混沌性的识别可以通过观察关联维数是否具有饱和现象来完成.本文采用G-P算法求关联维数［20-21］.

图3 给出了Δt=5，7，10，15 min 的交通流量时间序列的ln Cm(r)-ln r关系图，图中:r为相空间中相点之间欧氏距离的阀值;Cm(r)为关联积分函数，具体含义详见文献［18］.

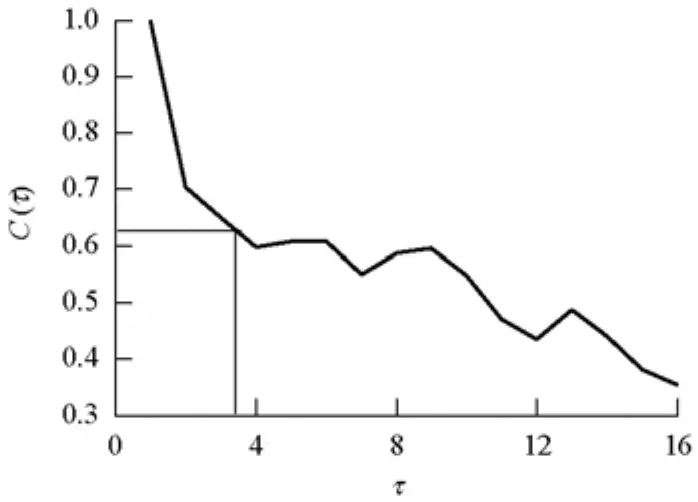
图2 Δt=10 min时的自相关系数函数Fig.2 The auto correlative function of Traffic flow time series of 10 min

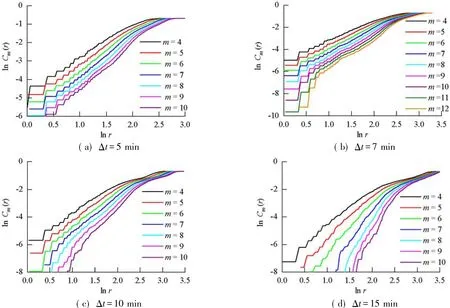
图3 ln Cm(r)-ln r曲线Fig.3 Curve of ln Cm(r)-ln r

图4 为4组交通流量时间序列的关联维数随嵌入空间维数m的变化曲线.4组不同采样间隔的交通流量时间序列关联维数D2(m)随着嵌入维数的增加均出现饱和现象，且各时间尺度时间序列均满足D2(m)不是整数或大于2的条件，这说明空中交通流表现出一种对初始条件敏感的混沌振荡［18］.所以，可以判定4组时间序列均为混沌时间序列.

3.2 预测结果对比及分析

按第2节中的步骤1，分别求出4组交通流量时间序列时间延迟τ和嵌入维数m，如表1所示.依据这些参数对各组时间序列进行相空间重构.以Δt=10 min的流量时间序列为例，重构的相空间拥有102相点，进行第1步预测时的预测中心相点为X102=(9，8，11，7，3，10，8).

按照步骤2，利用本文改进的一阶局域预测方法得到演化一步后的相点预测值103=(8.04，8.24，7.64，8.43，9.23，7.84，8.24)，其第 m 个分量即为第 1个 10 min内的流量预测值121.因为Δt=10 min的流量时间序列的m=7，所以21=8.24.

由1.3节介绍的方法生成误差序列(3.04，4.24，－3.35，－1.56，6.23，－3.15)，并得到一步平滑外推值 Δx=－4.24.因此，由^'121=^X121－Δx得到修正后的预测值，即该扇区20:00—20:10这段时间内的流量值'121=12.48，步骤 3 到此结束.将预测得到的新流量值加入原流量时间序列，并不断重复步骤4，直到最终得到所有后4 h的流量预测结果.

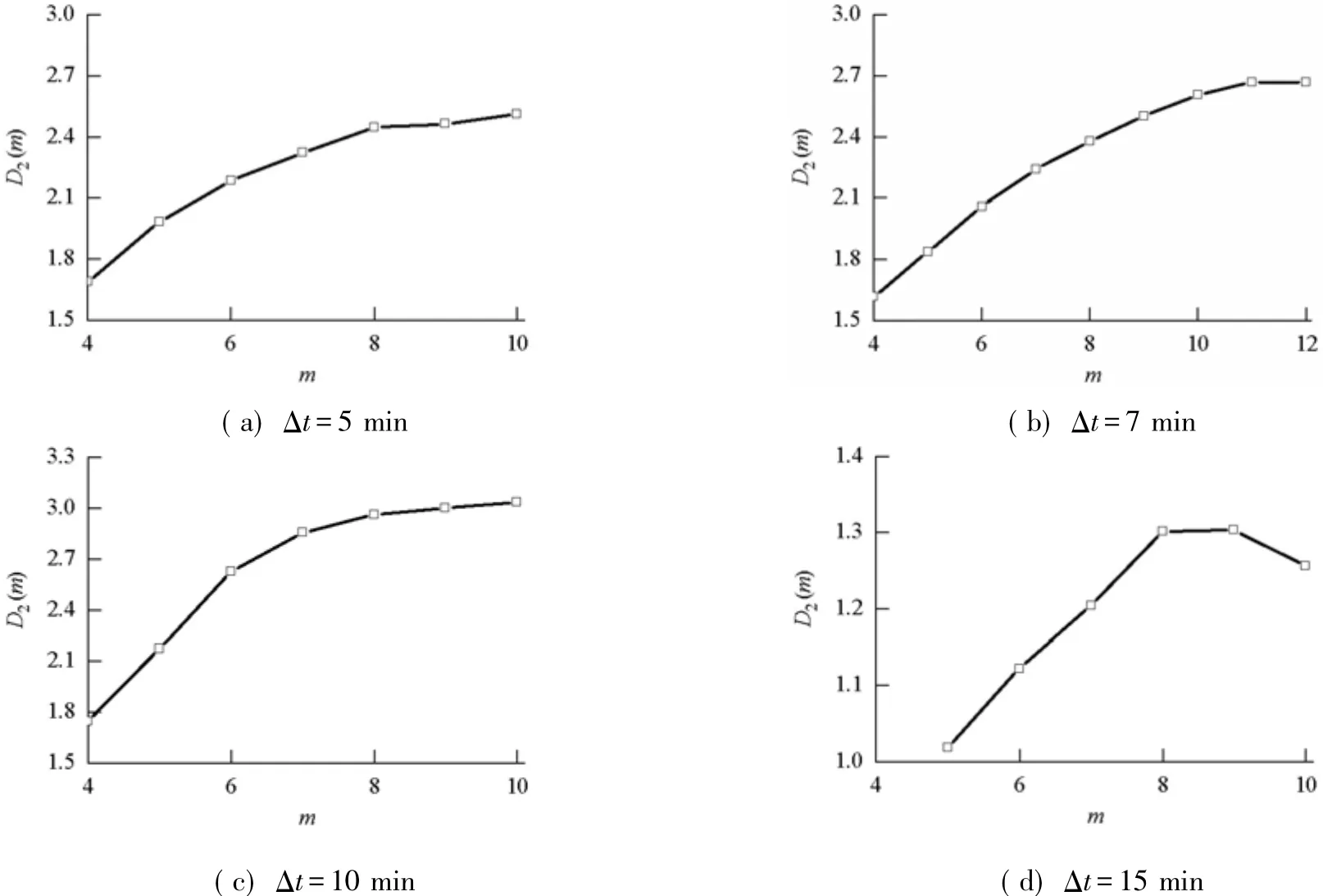
图4 关联维数随嵌入维数的变化曲线Fig.4 Curve of D2(m)with different m

表1 不同时间尺度空中交通流量时间序列的时间延迟和嵌入维数Tab.1 Time delay and Embedding dimension of Air traffic flow time series under different time scales

上述过程阐述了应用预测模型的过程，按照上述过程分别对其他3组时间序列进行预测.图5将交通流量的预测值和实际值进行对比给出了预测结果.由图5可知，4组不同时间尺度的交通流量预测值曲线和实际值曲线基本吻合，表明本文提出的改进型预测方法适用于不同统计时间间隔生成的空中交通流量时间序列预测.

为了对预测结果的准确性进行评价，采用平均绝对误差EAAE和相对误差ERE来衡量预测精度，即

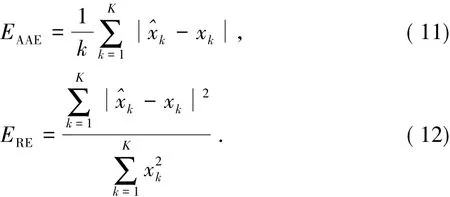
图6和图7给出了4组交通流量时间序列的预测精度.由图6、7可知，改进后的方法有效地提高了改进前方法的预测准确性.以Δt=10 min为例，改进前的预测方法ERE=0.148 1，改进后的预测方法 ERE=0.104 1，相对误差减小了 29.7%.通过对比不同尺度的空中交通流量预测效果，有如下发现:

(1)不同时间尺度的交通流量时间序列之间的预测误差相差较大，说明在进行空中交通流量预测时时间尺度的选择对预测精度有很大影响.预测模型对Δt=5，7，10 min这3组样本数据的预测精度依次增高，当Δt=10 min时预测效果达到最好，当Δt=15 min时预测模型预测精度开始出现降低趋势，预测精度较差.所以，在以后的空中交通流量预测的研究及应用中需要科学地选取适当的时间序列标度.

(2)相对误差随着交通流量时间序列标度的增大而减小，而平均绝对误差随着交通流量时间序列标度的增大而增大.这是由两种评价指标表现误差的侧重点不同造成的.流量的平均绝对误差反映的是测量流量的可信程度，流量的相对误差则确切地表示了预测流量值偏离真实流量值的实际大小.所以实际应用中应根据不同的预测要求，选择不同的评价指标，从而选取能达到更理想预测效果的时间尺度的时间序列进行预测.当关注每一步预测的流量偏离值时，选用平均绝对误差作为评价指标，此时，选择较小时间尺度交通流量预测效果较理想.当希望预测流量的总体误差比例更小时则选用相对误差作为评价指标，此时，选择较大Δt的交通流量预测效果更理想.

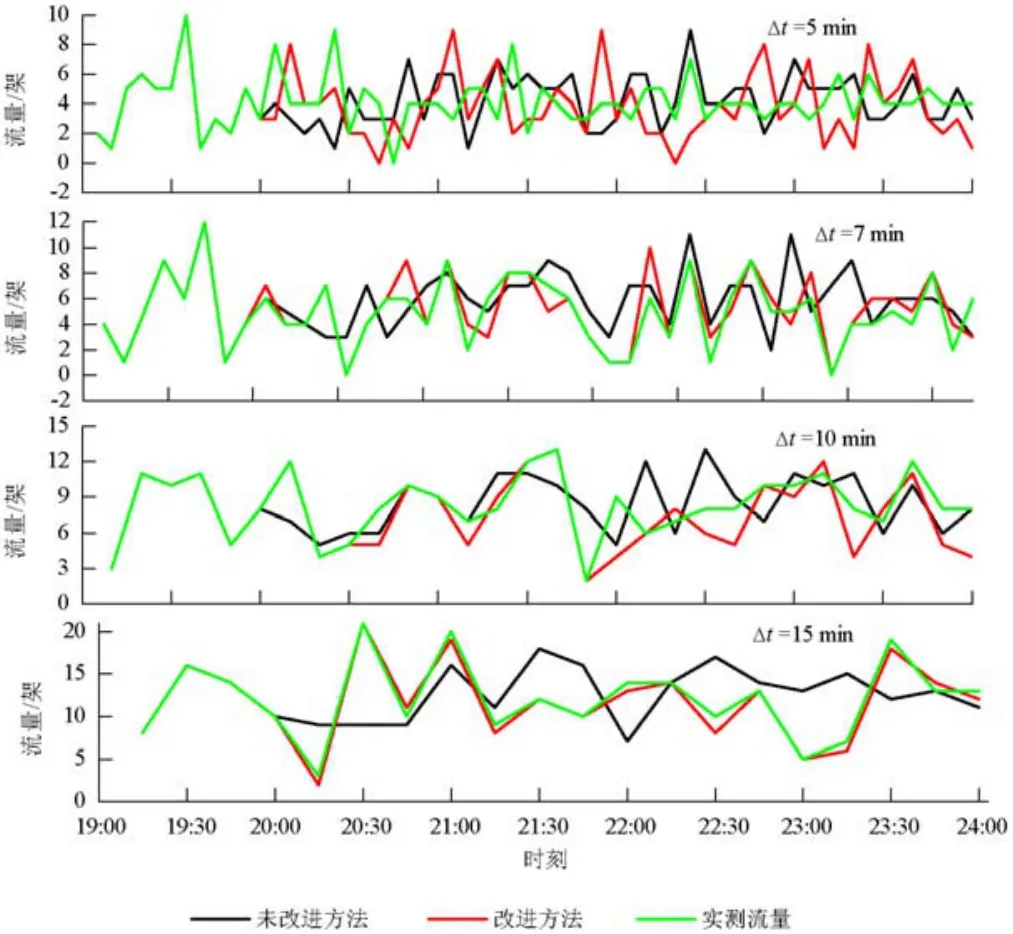
图5 空中交通流量的实际值和预测值对比Fig.5 Predicted and actual values of air Traffic volume

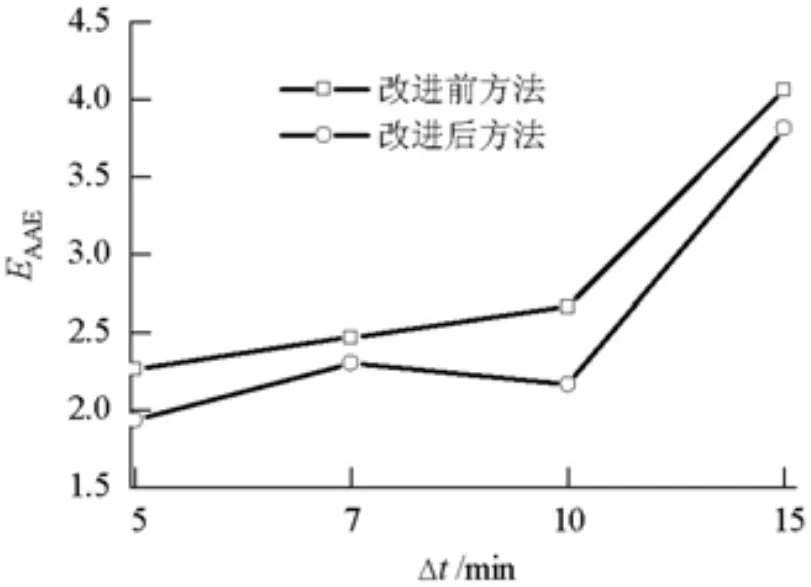
图6 空中交通流量预测的平均绝对误差对比Fig.6 Comparison Average absolute error of Air traffic flow prediction

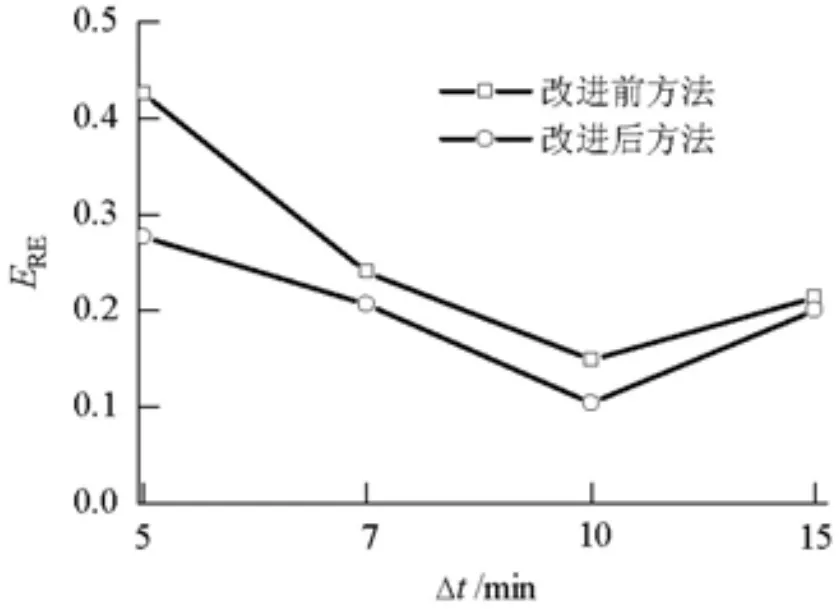
图7 空中交通流量预测的相对误差对比Fig.7 Comparison Relative error of Air traffic flow prediction

4 结束语

本文在混沌时间序列的加权一阶局域预测方法的基础上提出了一种临近相点演化加权的改进预测方法，并将其应用到空中交通流量预测领域.此外，还引入了基于误差序列的误差修正方法对预测误差进行修正，在一定程度上修正了预测误差，减小了预测过程中误差的累积.预测实例中利用G-P算法求出时间序列的关联维数，发现其随着嵌入维数的增加而出现饱和现象，证明了空中交通流量时间序列存在混沌特性.随后采用改进预测方法对样本混沌流量时间序列进行4 h预测，结果表明改进的加权一阶局域预测方法不仅能够有效预测交通流量且提高了预测精度.

研究过程中发现该预测方法还有许多值得深入探究之处，例如是否相点间欧氏距离越小其演化趋势就越相似，所以最邻近点的选择方法必须科学反映相点间的邻近程度［14］，改进欧式距离法使其能更科学地反映邻近点和预测中心点关联程度.此外，统计间隔对结果的影响本文只是做了简单的定性分析，研究发现空中交通流量时间序列相邻采样点间存在较强的自相关性，统计间隔对预测精度影响的内在机理还有待在日后的研究工作中深入研究.

［1］ 耿睿，崔德光，徐冰.应用支持向量机的空中交通流量组合预测模型［J］.清华大学学报:自然科学版，2008，48(7):1205-1208.GENG Rui，CUI Deguang，XU Bing.Support vector machine-based combinational model for air traffic forecasts［J］.Journal of Tsinghua University，2008，48(7):1205-1208.

［2］ 张明，韩松臣，黄林源.基于双重力模型和人工神经网络的空中交通流量组合预测［J］.西南交通大学学报，2009，44(5):764-770.ZHANG Ming，HAN Songchen，HUANG Linyuan.Air traffic flow combinational forecast based on double gravity model and artificial neural network［J］.Journal of Southwest Jiaotong University，2009，44(5):764-770.

［3］ 王超，郭九霞，沈志鹏.基于基本飞行模型的4D航迹预测方法［J］.西南交通大学学报，2009，44(2):295-300.WANG Chao，GUO Jiuxia，SHEN Zhipeng.Prediction of 4D trajectory based on basic flight models［J］.Journal of Southwest Jiaotong University，2009，44(2):295-300.

［4］ 吕金虎，张锁春.加权一阶局域法在电力系统短期负荷预测中的应用［J］.控制理论与应用，2002，19(5):767-770.L Jinhu，ZHANG Suochun.Application of addingweight one-rank local-region method in electric power system short-term load forecast［J］.Control Theory ＆Applications，2002，19(5):767-770.

［5］ 金玉婷.基于混沌和小波神经网络的短时交通流量预测方法研究［D］.成都:西南交通大学，2014.

［6］ 陈丹，胡明华，张洪海，等.考虑周期性波动因素的中长期空中交通流量预测［J］.西南交通大学学报，2015，50(3):562-568.CHEN Dan，HU Minghua，ZHANG Honghai，et al.Forecast method for medium-long term air traffic flow considering periodic fluctuation factors［J］.Journal of Southwest Jiaotong University，2015，50(3):562-568.

［7］ 张洪海，杨磊，别翌荟，等.终端区进场交通流广义跟驰行为与复杂相变分析［J］.航空学报，2015，36(3):949-961.ZHANG Honghai， YANG Lei， BIE Yi Hui， et al.Analysis on generalized following behavior and complex phase-transition law of approaching traffic flow in terminal airspace［J］.Acta Aeronautica et Astronautica Sinica，2015，36(3):949-961.

［8］ PACKARD N H，CRUTCHFIELD J P，FARMER J D.Geometry from atime series［J］.PhysicsReview Letters，1980，45(9):712.

［9］ 吕金虎，陆君安，陈士华.混沌时间序列分析及应用［M］.武汉:武汉大学出版社，2002:102-105.

［10］ CONG W，HU M H.Chaotic characteristic analysis of air traffic system［J］. Transactions of Nanjing UniversityofAeronautics ＆ Astronautics， 2014，31(6):636-642.

［11］ LI S M，XU X H，MENG L H.Flight conflict forecasting based on chaotic time series［J］.Transactions of Nanjing University of Aeronautics＆Astronautics，2012，29(4):388-394.

［12］ 王超，郑旭芳，王蕾.交汇航路空中交通流的非线性特征研究［J］.西南交通大学学报，2017，52(1):171-178.WANG Chao，ZHENG Xufang，WANG Lei.Research on nonlinear characteristics of air traffic flows on converging air routes［J］.Journal of Southwest Jiaotong University，2017，52(1):171-178.

［13］ STROGATZ S H.Nonlinear dynamics and chaos:with applicationsto physics， biology， chemistry， and engineering［M］.Boulder:Westview Press，2014:317-335.

［14］ XUE J，SHI Z.Short-time traffic flow prediction based on chaos time series theory［J］.Journal of TransportationSystemsEngineering＆ Information Technology，2008，8(5):68-72.

［15］ LAN L W，SHEU J B，HUANG Y S.Investigation of temporal freeway traffic patterns in reconstructed state spaces［J］.Transportation Research Part C Emerging Technologies，2008，16(1):116-136.

［16］ TAKENS F.On the numerical determination of the dimension of an attractor［M］.Berlin:Springer，1985:99-106.

［17］ MA R.On the dimension of the compact invariant sets of certain non- linear maps［M］. Berlin:Springer，1981:230-242.

［18］ 贺国光，马寿峰，冯蔚东.对交通流分形问题的初步研究［J］.中国公路学报，2002，15(4):82-85.HE Guoguang， MA Shoufeng， FENF Weidong.Preliminary study of fractals of traffic flow［J］.China Journal of Highway＆ Transport，2002，15(4):82-85.

［19］ 马庆禄.基于混沌理论的交通状态预测研究［D］.重庆:重庆大学，2012.

［20］ KANTZ H，SCHREIBER T.Nonlinear time series analysis［M］. Cambridge: Cambridge University Press，2004:69-72.

［21］ GRASSBERGER P，PROCACCIA I.Measuring the strangeness of strange attractors［J］. Physica D Nonlinear Phenomena，1983，9(1):189-208.