RES脉内特征的差分进化粒子群投影寻踪评价模型

朱 斌， 金炜东， 余志斌

(1.长江师范学院电子信息工程学院，重庆408100;2.西南交通大学电气工程学院，四川成都610031)

雷达辐射源信号(radar emitter signal，RES)脉内特征综合评估是现代雷达对抗中急需解决的新问题.现代雷达对抗信号环境中辐射源数量多、分布密度大、信号交叠严重，传统的信号识别方法很难适应现代战场复杂的电磁环境［1］.RES分选识别研究是雷达电子对抗领域中非常重要而又非常困难的课题，也是一项非常紧迫的任务.为此，研究人员通过脉内特征来实现信号的分类识别，效果显著［2-5］，但目前迫切需要对这些脉内特征的效能进行客观、有效的评估与甄别.

在RES脉内特征综合评估方面，邓延丽等提出了基于类别距离和Bhattacharyya距离、基于聚集离散性与可分性的雷达信号特征评价以及logistic回归评估模型［6-8］，方法局限于利用距离测度对特征的可分选性进行单一指标的评估，不能反映特征的综合效能.吴思东等引入多元集对分析对该问题进行研究［9］，但指标体系中引入指标灵敏度值得商榷，因为在参数变化时，不同特征聚类的变化是否有利于分类识别不能确定，无法判断特征的灵敏度是否有益于信号识别，此外，该方法建立在层次分析法的基础上，评估结果不够客观.徐璟等提出雷达辐射源信号识别结果评估方法［10-12］，通过识别结果间接反映特征效能，与分类器的选择密切相关，依然没有走出以往依靠识别结果来评价特征的老路，特征评估的效度受到质疑.总体而言，以往的雷达辐射源信号脉内特征综合评估存在标准单一［13-14］，评估方法或模型不客观等诸多问题［15-16］.为此，本文提出基于差分进化粒子群投影寻踪算法的RES脉内特征综合评估模型，通过建模将RES脉内特征评估问题转化为有条件限制的多元非线性目标函数的优化问题，并将改进的粒子群优化算法与差分进化算法相结合，用于实现对目标函数的寻优，最终实现对RES脉内特征的有效、客观评估.

1 问题模型

投影寻踪(projection pursuit，PP)算法是直接由样本数据驱动的高维数据分析算法，能揭示数据的线性和非线性结构.PP算法对分析数据没有正态和线性假设的前提限制，非常适于多维非线性、非正态数据的分析和处理，已在很多领域取得成功应用［17-18］.前期研究成果表明雷达辐射源信号脉内特征向量不具有正态分布特性［19］，同时RES脉内特征具有非线性和多维的特点，因此采用PP算法来研究RES脉内特征评估这一新问题非常适合.

设有l个不同类型雷达辐射源信号组成的集合为S={s1，s2，…，sl}，不同类型雷达辐射源信号脉内特征集 Fm={f1，f2，…，fq}，m=1，2，…，l;q∈Z+，q为特征类型数，评估指标集 K={k1，k2，…，kp}，p∈Z+，p 为指标的个数.

A=(af1，af2，…，afq)为不同 RES 脉内特征参照评估指标K计算得到的评估值.假定评估指标的权重w=(w1，w2，…，wp)已知，则综合评估矩阵 E可通过式(1)计算.

根据E的计算结果，可实现对不同雷达辐射源信号脉内特征的综合评估.

假定沿某投影方向

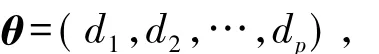
将RES脉内特征评估数据

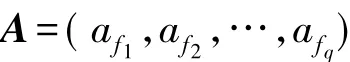
投影到低维子空间上，可得到评估数据的一维投影值V(h)，如式(2)所示.

对于投影采用的构形，可用投影指标函数J(θ)来评价该投影揭示原系统某种分类排序结构的可能性大小，并寻找出使J(θ)达到最能反映高维数据结构或特征的投影值，最后根据该投影值来分析高维数据的结构特征.一般地，根据{V(h)}的散点分布图可进行判定:要求同类RES脉内特征的V(h)值散点分布尽可能集中，不同RES脉内特征的V(h)值散点分布尽可能分开.因此，投影指标函数构造如下:

式中:SV为 V(h)的标准差;DV为 V(h)的局部密度.

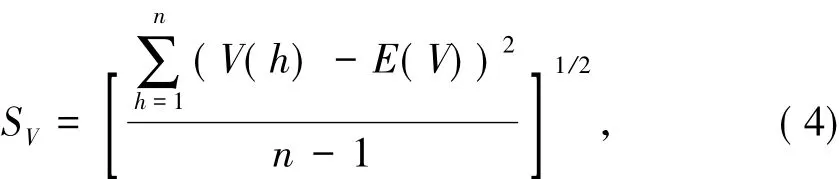
式中:E(V)为投影序列{V(h)}均值.

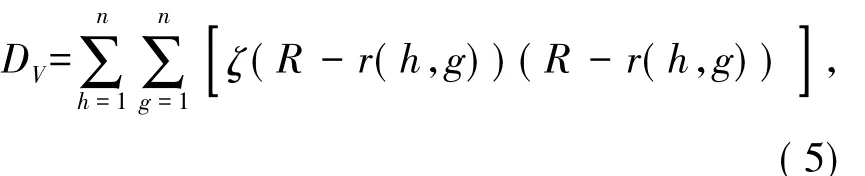
式中:R为局部密度窗半径，通常取0.1SV;r(h，g)为类内密度，用投影序列值之间的距离计算:

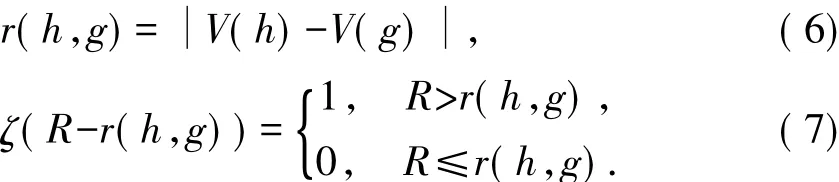
在RES脉内特征评估参数给定的情况下，J(θ)会随着投影方向θ的变化而变化.θ中蕴含着数据的不同结构特征，最佳投影方向即是最能揭示高维数据特征结构的投影方向.同时，评估等级分类要求在某投影方向上的散度和局部密度都较大时，体现的分类效果最显著，即J(θ)函数达到最大值时的投影方向就是最佳投影方向.因此，令

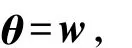
则RES脉内特征评估问题可描述为一个有条件限制的多元非线性函数的优化问题:

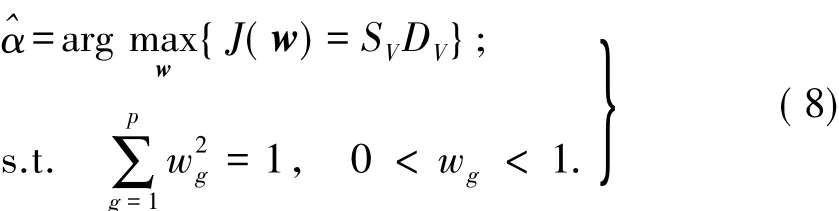
2 改进的差分进化粒子群算法

如式(8)所示，借助投影寻踪算法建立起来的RES脉内特征综合评估模型是一个有条件限制的多元非线性函数.有条件限制的多元非线性函数的求解采用传统方法相对比较困难，普遍采用智能优化算法来进行求解，粒子群优化(particle swarm optimization，PSO)算法就是其中之一.尽管标准的粒子群算法(standard particle swarm optimization，SPSO)有诸多优点，但存在易陷入局部极值、搜索精度不高、进化后期收敛速度慢等问题［20］.因此，本文对SPSO算法进行了改进，对SPSO算法的权重做变权处理，得到改进的粒子群优化(advanced particle swarm optimization，APSO)算法.由于基于群体智能的标准粒子群算法本身容易早熟，且在算法后期容易在全局最优解附近振荡［21］.为了保证RES脉内特征评估的多元非线性函数模型的优化求解，对SPSO算法的惯性权重可调参数w做变权处理，权重变换按式(9)进行.很显然，算法迭代初期惯性权重较大，利于算法跳出局部极值点进行全局搜索;后期惯性权重较小，利于算法在当前局部极值点附近进行有效搜索，从而提高SPSO算法的全局和局部搜索能力，改善SPSO算法的优化能力.

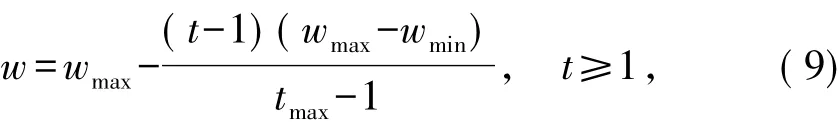
式中:wmax为权重w最大值;wmin为权重w最小值;tmax为最大迭代次数;t为当前迭代次数.

改进后的粒子i第d维的速度和位置更新分别按如下方式进行:

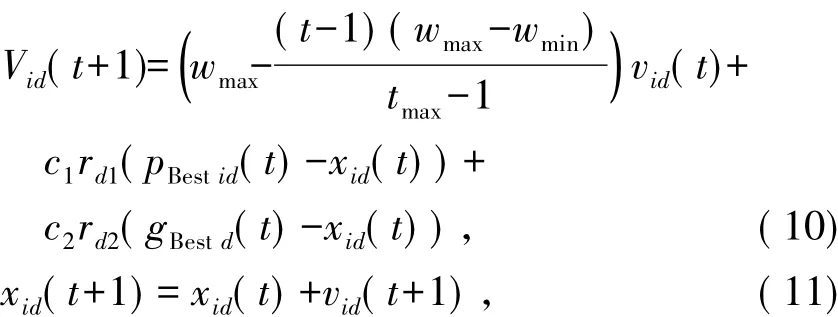
式中:c1、c2为加速系数;rd1和 rd2是［0，1］区间上两个随机数.每次迭代，粒子通过跟踪个体极值pid和全局极值pgd来更新自己.

将APSO算法与差分进化(differential evolution，DE)算法相结合，得到改进的差分进化粒子群优化(advanced differential evolution particle swarm optimization，ADEPSO)算法，最后将ADEPSO算法用于评估问题数学模型多元非线性函数的优化求解.ADEPSO算法流程如图1所示.

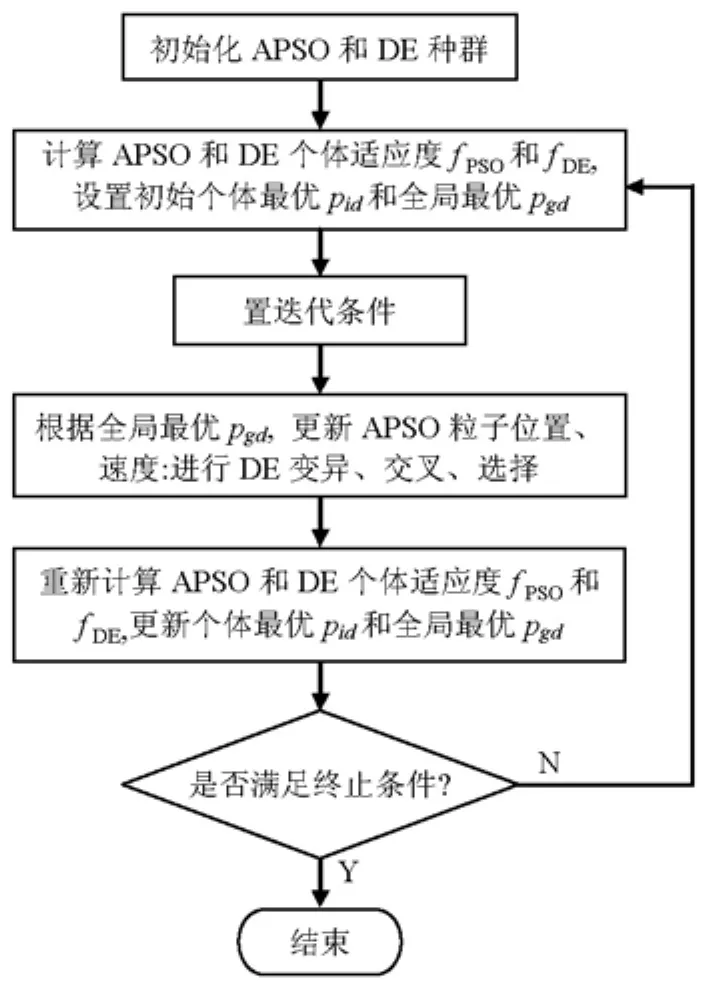
图1 ADEPSO算法流程Fig.1 Flow char t of ADEPSO algorithm

3 特征评估模型

RES脉内特征的改进差分进化粒子群投影寻踪(advanced differential evolution＆particle swarm optimization projection pursuit，ADEPSOPP)评估模型如图2所示.算法具体步骤如下:

(1)参照评估体系计算获取RES脉内特征评估指标参数.

(2)评估参数的归一化处理.设q、p分别表示样本的容量和指标数，x*(α，β)和y(α)分别为第α个样本的第β个指标参数值及相应的评估等级，α=1，2，…，q;β=1，2，…，p.xmin(β)、xmax(β)分别表示第β个指标参数的最大值和最小值，评估参数的归一化分别依照式(12)和式(13)进行.

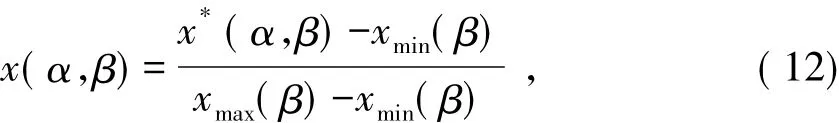
式中:x*(α，β)为效益型指标;

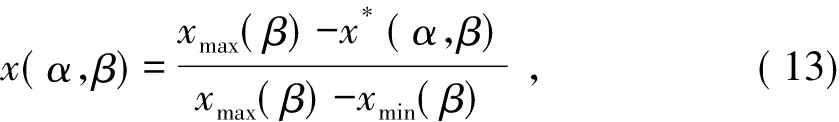
式中:x*(α，β)为成本型指标.

(3)投影目标函数建模.应用投影寻踪算法构造RES脉内特征评估的投影目标函数.

(4)投影目标函数的优化求解.用改进的差分进化粒子群优化算法求解RES脉内特征评估的多元非线性函数，求得最佳投影方向.

(5)权重确定.根据最佳投影方向向量计算获得评估指标的权重，计算RES脉内特征的综合评

估值，根据评估值计算结果即可分析特征效能的优劣.

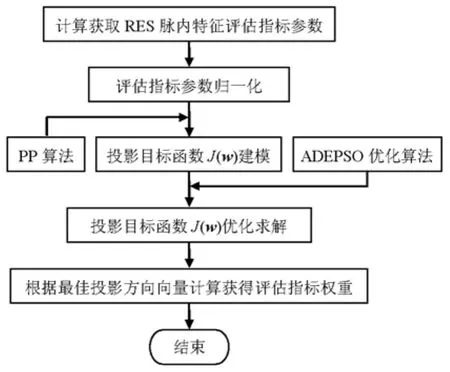
图2 RES脉内特征的ADEPSOPP评估模型Fig.2 ADEPSOPP evaluation model of RES intrapulse features

4 仿真分析

分析表明实现RES脉内特征综合评估的关键是评估数学模型的求解，即能否获得评估的最佳权重.为验证模型的有效性，实验对模型求解算法改进前后的算法性能做了对比试验分析，同时针对实际的评估问题，将本算法与其他优化算法的求解结果做了对比分析.

4.1 算法性能分析

选取3种典型测试函数:Rosenbrock函数、Rastrigrin函数和 Girewank函数做测试分析.Rosenbrock函数是单峰函数，极值搜索较慢且不易获得全局最优，可有效检测算法的局部搜索能力;Rastrigrin函数和Girewank函数是多峰函数，局部极值较多，可有效检测算法的全局搜索能力.

不同算法的种群规模psize=40，最大迭代次数5 000次.SPSO 算法的参数设置为:w=0.9，c1=c2=2.APSO 算法的参数设置为:wmax=0.9，wmin=0.4，c1=c2=2.DE 算法的参数设置为:交叉因子 cr=0.9，缩放因子f=0.5.ADEPSO算法参数设置与APSO算法和DE算法中的设置相同.每个测试函数实验运行30次，实验结果如表1所示，针对3种测试函数的适应度值优化曲线分别如图3～5所示.

从表1可知，对Rastrigrin函数和Girewank函数，ADEPSO算法的最优适应度值均为 0，说明ADEPSO算法已经求得这两个测试函数的最优极值.而Rosenbrock函数是一个用来测试优化算法性能的非凸函数，极值位于一个相对平坦的区域，获得全局最优相当困难.因此，Rosenbrock函数全局极值就是在所有粒子个体极值中的最小值，即全局最优粒子的位置.从表1可以看出，ADEPSO算法求得的Rosenbrock函数最优极值最小，因此，与其他算法相比，ADEPSO算法全局寻优效果最好.

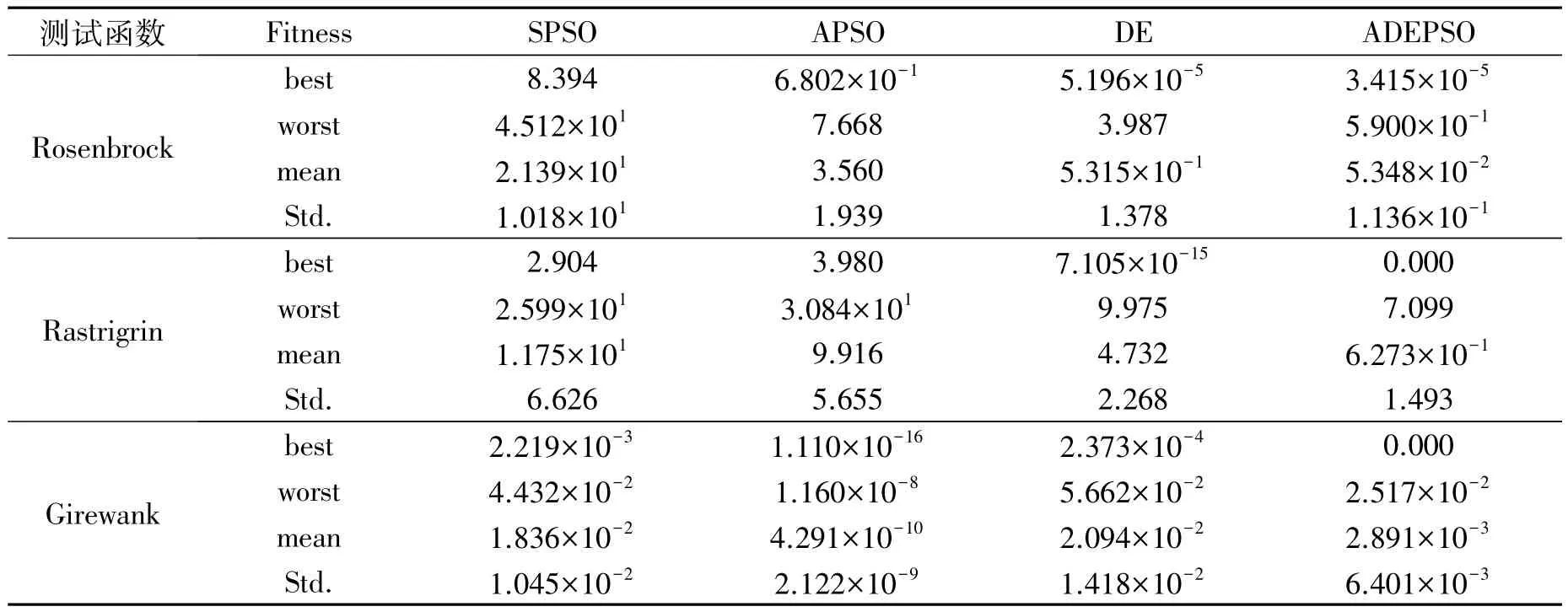
表1 基于标准测试函数的不同算法的测试结果Tab.1 Test results of different algorithms based on standard test functions

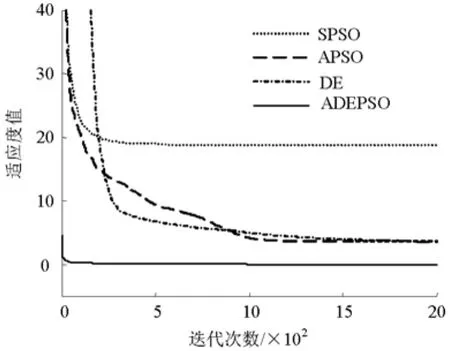
图3 Rosenbrock函数适应度值优化曲线Fig.3 Fitness optimization curve of Rosenbrock function

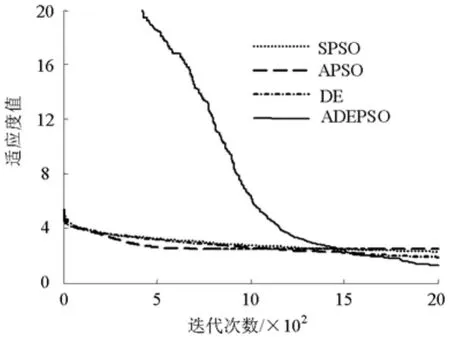
图4 Rastrigrin函数适应度值优化曲线Fig.4 Fitness optimization curve of Rastrigrin function

根据图3可看出，ADEPSO算法的搜索精度和收敛性均优于SPSO、APSO和DE算法，同时根据表1适应度方差值可看出，ADEPSO算法的鲁棒性优于SPSO、APSO和DE算法.

Rastrigrin函数和Girewank函数都是多峰函数，对算法的全局搜索能力要求较高，从图4和图5可以看出，ADEPSO算法的收敛性较好，其求解精度是所有算法中是最好的.同时从表1也可以看出，ADEPSO算法总能找到测试函数的最优极值，其鲁棒性也较好.

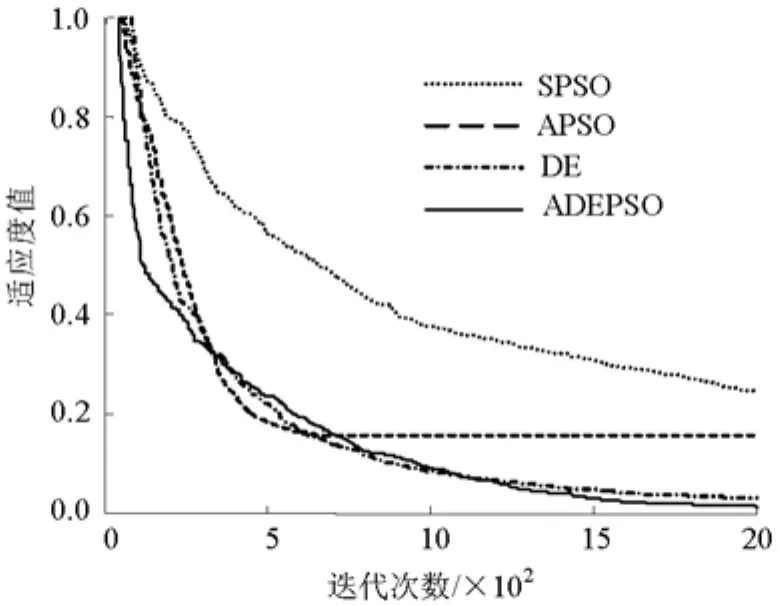
图5 Girewank函数适应度值优化曲线Fig.5 Fitness optimization curve of Girewank function

4.2 算法优化结果对比分析

选取雷达辐射源信号的相像系数(resemblance coefficient，RC)特征、小波灰度矩(wavelet gray moment，WGM)特征、瞬频派生 (instantaneous frequency，IF)特征和 LFM、NLFM、BPSK、FSK、QPSK 5种典型雷达辐射源信号进行仿真分析.评估指标分别为特征类内欧氏距离总和C1、特征的欧氏距离方差C2、特征类间欧式距离总和C3、特征的时间复杂度C4、特征的空间复杂度C5、特征的稳健性 C6.实 验 平 台:Thinkpad X230，处 理 器2.4 GHz，内存4 GB，信号载频为 10 MHz，脉宽20 μs，抽样频率 100 MHz，SNR 为 10 db;LFM 带宽为2 MHz，FSK、BPSK和QPSK的编码规则分别为［0110010］、［1110010］和［0，0，0，0，0，π/2，π，3π/2，0，π，0，π，0，3π/2，π，π/2］，NLFM 为正弦调制信号.每种特征提取算法下，每种雷达辐射源信号各提取3组特征向量，每组50个，计算得到归一化后的投影原始数据见表2.

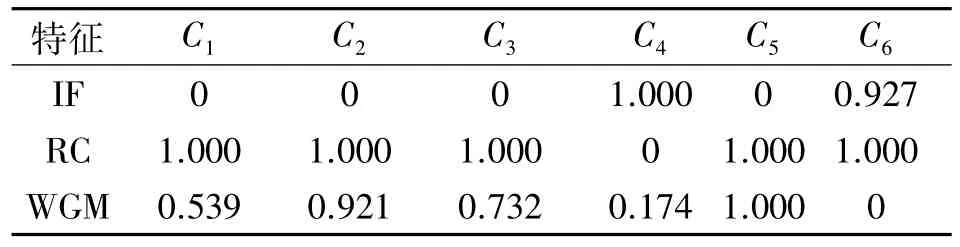
表2 归一化处理后的投影数据Tab.2 The normalized projection data

分别用文献［16］中的实数编码加速遗传算法(real-coded accelerating genetic algorithm，RAGA)和本文算法对投影目标函数进行求解.RAGA算法的参数设置与文献［16］相同，即种群规模为400，加速次数20次，交叉概率为 0.9，变异概率为 0.1，密度窗宽为指标样本的0.1倍均方差，RAGA算法搜索次数为50次，两种算法先后5次计算的结果如表3所示.

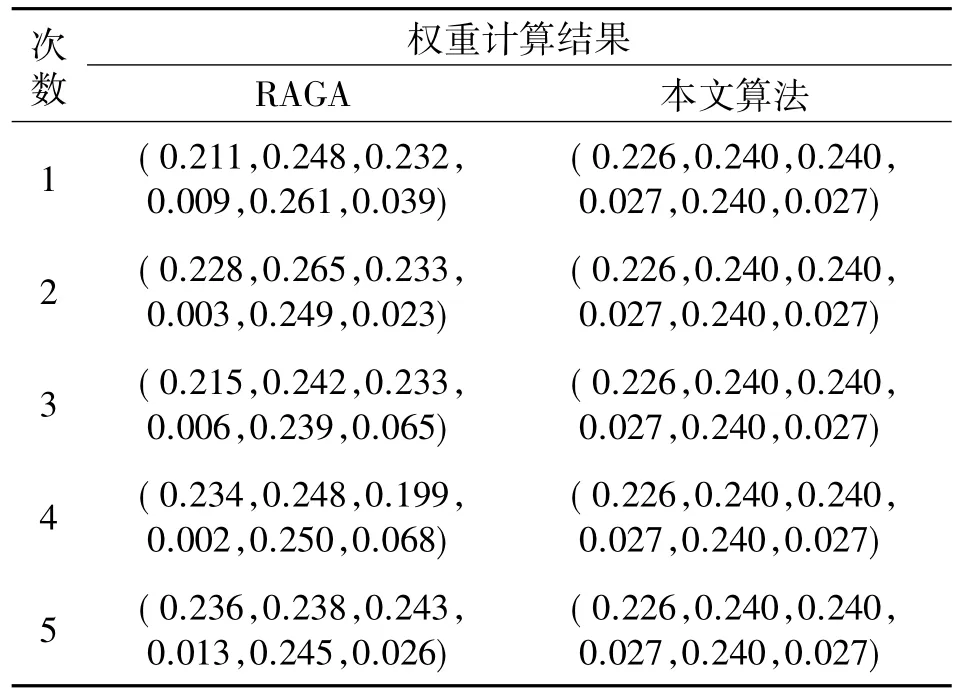
表3 不同算法的权重优化结果Tab.3 The weight optimization results of different algorithms

从表3可以看出，RAGA算法对问题模型函数的优化求解结果是变化的，每次计算结果均存在波动，这是因为RAGA算法对问题模型函数的优化求解结果不是最优，计算陷入局部极值导致的，因此会存在计算结果波动的情况，权重确定需要人为修正，这必然会影响到评估模型的客观性.本文算法每次计算的结果均保持不变，说明本文算法对问题模型函数的优化求解没有陷入局部极值，计算结果是最优的，权重确定不需要人为干预，从而保证了评估模型的客观性.对问题模型函数的优化结果从另一个角度证明了ADEPSO求解算法能够获得问题模型函数的最优解，即实现评估权重的寻优.根

据计算结果，得到各指标权重如下:

将评估数据与优化得到的权重w结合，计算得到RES脉内特征综合评估值矩阵:

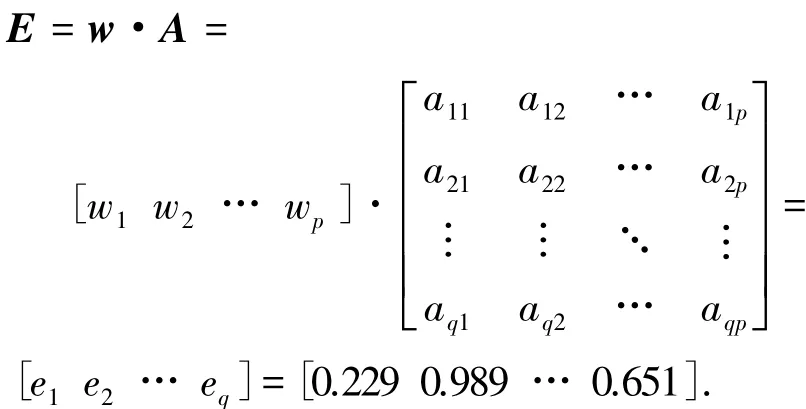
根据综合评估计算结果，可以判定RES相像系数特征优于小波灰度矩特征和瞬频派生特征，小波灰度矩特征优于瞬频派生特征.

5 结 论

雷达辐射源信号脉内特征综合评估是目前雷达电子对抗亟待解决的新难题，针对这一问题，本文提出一种新的雷达辐射源信号脉内特征综合评估模型——ADEPSOPP评估模型.通过借助投影寻踪算法建立起RES脉内特征综合评估的数学模型，将脉内特征综合评估问题转化为有条件的多元非线性目标函数的优化问题，并通过改进粒子群算法与差分进化算法的结合实现了投影寻踪算法投影方向的寻优.仿真结果表明:该群体智能算法对Rosenbrock测试函数的最优适应度值最小，对Rastrigrin函数和Girewank测试函数的最优适应度值为0，说明该算法的计算精度优于其他算法;同时适应度值的方差比标准粒子群算法和差分进化算法小，说明该算法的收敛性和鲁棒性较好;通过与加速遗传算法对评估问题目标函数5次优化结果的比较，本算法的计算结果没有波动，说明基于群体智能的RES脉内特征综合评估模型能够更客观、更有效地实现对RES脉内特征的综合评估.

致谢:长江师范学院人才引进计划资助项目(2016KYQD 10).

［1］ GUO Qiang，QU Zhenshen，WANG Changhong.Pulseto-pulse periodic signal sorting features and feature extraction in radar emitter pulse sequences［J］.Journal of Systems Engineering and Electronics，2010，21(3):382-389.

［2］ GUO Qiang，NAN Pulong，ZHANG Xiaoyu，et al.Recognition of radar emitter signals based on SVD and AF main ridge slice［J］.Journal of Communications and Networks，2015，17(5):491-498.

［3］ 白航，赵拥军，胡德秀.时频图像局部二值模式特征在雷达信号分类识别中的应用［J］.宇航学报，2013，34(1):139-146.BAI Hang，ZHAO Yongjun，HU Dexiu.Radar signal recognition based on the local binary pattern feature of time-frequency image［J］.Journal of Astronautics，2013，34(1):139-146.

［4］ ZHU Bin，JIN Weidong，YU Zhibin.Texture feature extraction of advanced radar emitter signals［J］.ICIC Express Letters，2014，8(9):2383-2387.

［5］ 王世强，张登福，毕笃彦.双谱二次特征在雷达信号识别中的应用［J］.西安电子科技大学学报，2012，39(2):127-132.WANG Shiqiang，ZHANG Dengfu，BI Duyan.Research on recognizing the radar signal using the bispectrum cascade feature［J］.Journal of Xidian University，2012，39(2):127-132.

［6］ 邓延丽，金炜东，李家会，等.基于聚集离散性与可分性的雷达信号特征评价［J］.计算机应用，2013，33(7):1946-1949.

［7］ DENG Yanli，JIN Weidong，LI Jiahui，et al.Feature evaluation ofradarsignalbased on aggregation，discreteness and divisibility［J］.Journal of Computer Applications，2013，33(7):1946-1949.

［8］ 邓延丽，金炜东，余志斌.基于类别距离和Bhattacharyya距离的雷达信号特征评价［J］.计算机应用研究，2012，29(11):4079-4081.DENG Yanli， JIN Weidong， YU Zhibin.Feature evaluation of radar signal based on category distance and Bhattacharyya distance［J］.Application Research of Computers，2012，29(11):4079-4081.

［9］ 吴思东，朱明，付克昌.基于多元集对分析的辐射源信号熵特征评价［J］.电路与系统学报，2013，18(2):298-304.WU Sidong，ZHU Ming，FU Kechang.Entropy feature evaluation of radar emitter signals based on SPA［J］.Journal of Circuits and Systems，2013，18(2):298-304.

［10］ 徐璟，何明浩，陈昌孝.雷达辐射源信号识别结果评估方法研究［J］.电波科学学报，2014，29(2):300-304，315.XU Jing， HE Minghao， CHEN Changxiao.Performance evaluation method for radar emitter signals recognition［J］.Chinese Journal of Radio Science，2014，29(2):300-304，315.

［11］ 徐璟，何明浩，陈昌孝.基于理想排序的雷达信号识别效能评估方法［J］.电波科学学报，2015，30(3):554-559.XU Jing， HE Minghao， CHEN Changxiao.Effectiveness evaluation of signal recognition based on AHP-I2TOPSIS［J］. Chinese Journal of Radio Science，2015，30(3):554-559.

［12］ 徐璟，何明浩，郁春来.雷达辐射源信号识别效能评估的 I2TOPSIS方法［J］.信号处理，2015，31(3):253-258.XU Jing，HE Minghao，YU Chunlai.Effectiveness evaluation of radar emitter signal recognition based on I2TOPSIS［J］.Journal of Signal Processing，31(3):253-258.

［13］ YU Zhibin，CHEN Chunxia.The radar signal featureseparability model analysis［C］∥Advanced Materials Research.Guangzhou: ［s.n.］，2011，268/269/270:1484-1487.

［14］ ZHU B，JIN W D，YU Z B，et al.Feature separability evaluation for advanced radar emitter signals［C］∥Communications in Computer and Information Science.Shanghai:Springer-Verlag.2012:204-212.

［15］ 朱斌，金炜东，余志斌.复杂体制雷达辐射源信号特征的FAHP评价［J］.计算机工程与应用，2012，48(20):18-22.ZHU Bin，JIN Weidong，YU Zhibin.FAHP-based feature evaluation for advanced radar emitter signals［J］.Computer Engineering and Applications，2012，48(20):18-22.

［16］ 段美军，金炜东，杨志新.一种雷达辐射源信号多目标特征评价模型［J］.计算机应用研究，2012，29(8):2912-2914.DUAN Meijun，JIN Weidong，YANG Zhixin.Multiobjective characteristics evaluation modelofradar emitter signal［J］.Application Research of Computers，2012，29(8):2912-2914.

［17］ SU Yu，SHAN Shiguang，CHEN Xilin.Classifiabilitybased discriminatory projection pursuit［J］. IEEE Transactions on Neural Networks，2011，22(12):2050-2061.

［18］ ALADJEM M.Projection pursuitmixturedensity estimation［J］. IEEE Transactions on Signal Processing，2005，53(11):4376-4383.

［19］ ZHU B，JIN W，YU Z.The distribution characteristics analysis of advanced RES feature［C］∥Communications in Computer and Information Science.Singapore:Springer-Verlag.2013:429-434.

［20］ MADHUBANTI M， AMITAVA C. A hybrid cooperative- comprehensive learning based PSO algorithm forimage segmentation using multilevel thresholding［J］.Expert Systems with Applications，2008，34(2):1341-1350.

［21］ CHIAM S C，TAN K C，MAMUN A Al.A memetic model of evolutionary PSO for computational finance applications［J］.Expert Systems with Applications，2009，36(2):3695-3711.