基于PSO小波神经网络辅助卡尔曼滤波的BDS/INS定位
2018-01-18李卫东黄晨阳王新屏
李卫东,黄晨阳,刘 杨,王新屏
(大连交通大学电气信息学院,辽宁 大连 116023)
0 引言
在北斗定位系统(Beidou navigation satellite system,BDS)中,卡尔曼滤波是一种通过软件消除定位信号噪声的重要方法[1]。假如对列车运行模型构造不够精确,会导致卡尔曼滤波后信号的发散、失真等不良结果[2]。通过构建卡尔曼滤波的输入/输出小波神经网络,可以解决这些问题[3]。
本文结合文献[1]~文献[3]的优点,改进了小波神经网络的学习率。在此基础上,采用粒子群优化(particle swarm optimization,PSO)算法结合遗传算法(genetic algorithm,GA)优化的小波神经网络对实际问题进行建模。仿真试验证明了该方法的有效性。
1 基于卡尔曼滤波的BDS/INS组合定位
目前,我国BDS总体性能略低于全球定位系统(global positioning system,GPS),它的主要问题可能在于:定位精度低、易受到无线电的干扰、保密性和安全性弱、 数据传输率低。这些缺陷可以通过与惯性导航系统(inertial navigation system,INS)结合来补偿[4]。BDS/INS可以使北斗信号在由于遮挡或高强度干扰的情况下,能单独进行导航定位,从而保证导航的可靠性。北斗系统可以修正INS的输出信息,减少它随时间积累的误差,保证导航的精确性和工作的稳定性。
卡尔曼滤波是一种通过算法估计被提取信号的最优理论。自1980年以来,它被广泛应用于运载体的导航和定位系统中[5]。
它的原理可以简述为:假设Xk为tk时刻的被估计状态,Wk-1系统的驱动噪声序列驱动方程如下:
Xk=φk,k-1Xk-1+Γk-1Wk-1
(1)
对Xk的量测方程满足线性关系:
Zk=HxXk+Vk
(2)
状态一步预测:

(3)
状态估计:
(4)
滤波增益:
(5)
一步预测均方误差:
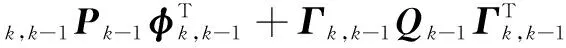
(6)
估计均方误差:
Pk=(I-KkHk)Pk/k-1
(7)


北斗定位系统与列车和地面设备时钟一致,并向其上的接收机发送用于导航定位的调制波。导航电文发送随机伪噪声。理想情况下,接收机接收到电文后,将它与卫星信号的原电文进行对齐处理,求得卫星与接收机的距离和列车的相关参数[6]。INS器件通过测量移动载体的运动加速度及位移,再通过积分运算,推导出列车相关参数。随后,BDS系统中的接收机将收到的相关列车参数,经电平转换后,通过通信电路传输到信号处理器进行处理。同时在数字信号的装置中将其中的惯性导航器件处理的信号导入,两者信息相融合。
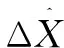
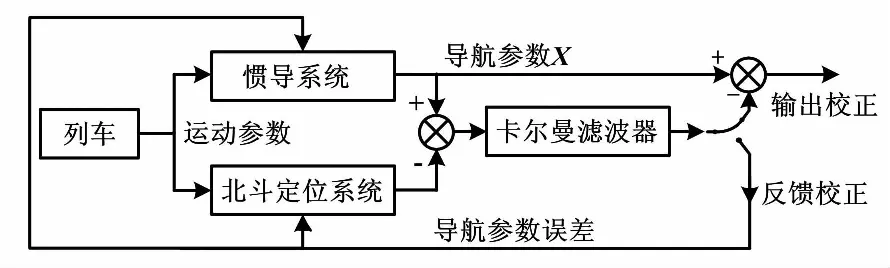
图1 BDS/INS结构图
2 小波神经网络辅助的卡尔曼滤波
2.1 卡尔曼滤波的不足及弥补方法
实际运行中,由于列车运动模型不能准确构造以及系统中存在硬件误差等原因,会导致经过卡尔曼滤波,获得的速度波形与实际速度波形有偏差,进而使得到的定位信息也不准确[8]。虽然这些误差的精确模型很难计算,但可以通过现有的卡尔曼滤波的输入/输出数据构造神经网络模型,再对这个神经网络模型进行校正。通过这种方式让北斗定位系统获取到较为准确的速度波形,从而提高北斗定位的精度。
采用图2所示的神经网络监督控制替换卡尔曼滤波。通过在线比较误差的方法对小波神经网络进行修正,逐步替换反馈控制器。在受到外界噪声或其他因素干扰的情况下,控制器的反馈将会再次发挥作用。神经网络监督控制方法,不但确保了控制系统能够比较稳定地运行,还有效提高了系统的精度及其自适应的能力[9]。

图2 神经网络监督控制图
2.2 小波神经网络结构
小波理论本身比较适合处理[10-11]小波神经网络(wavelet neural network,WNN)。与神经网络理论结合后,小波神经网络算法具有更加灵活有效的函数逼近能力以及较强的容错能力。其核心是将小波变换加入神经网络模型中,构造以“Sigmoid函数”为基本构架的小波神经网络。在构造小波神经网络时,因为小波分解能够进行平移,理论上能够逼近任意函数。
本文根据信号的特点,采用了融合型的小波神经网络。该网络主体为3层网络[12],具有单输入、单输出的结构,输入层为并行输入,隐含层、输出层包含了m个神经元。
小波神经网络结构如图3所示小波函数中的伸缩,平移参数a、b和神经网络参数都可以通过网络学习进行训练。图3中,隐含层神经元的激励函数f1是 Morlet 小波函数:
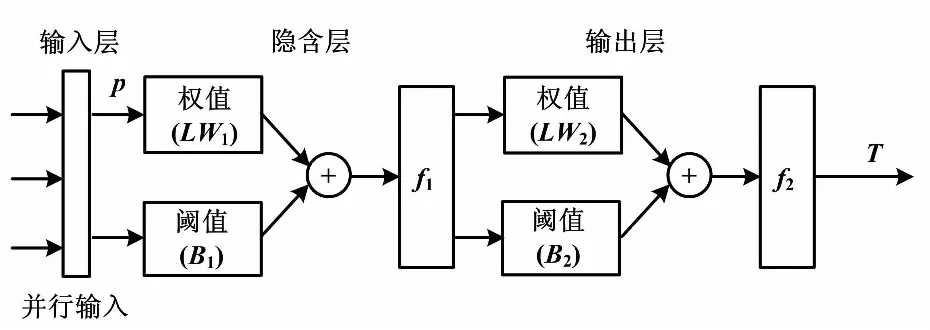
图3 小波神经网络结构图
(8)
隐含层输出为:
(9)
(10)
式中:O为隐含层的输出;x为输入层的输入;w为权值;h为Morlet小波函数。
输出层输出为:
(11)
2.3 改进的小波神经网络训练算法
本文采用了改进的梯度下降法[13],对小波神经网络权值和参数进行训练,误差函数为:
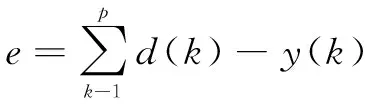
(12)
式中:d(k)为期望输出;y(k)为网络实际输出;p为样本数。
首先对输入数据进行分割,并行输入,得到权值平均值。这样权值的反复变化次数减少,不但节省了时间,也提高了系统的稳定性。神经网络主要基于误差修正来进行结构的调整和学习,学习率的改变会影响收敛的速度和训练的效果。如果学习率过小,系统的调节时间会太长;如果学习率太大,可能导致振荡或发散。随着时间增加,系统的调节幅度应相应减少。调整后的学习率单调增加且增加率逐渐变缓,log(a+x)无疑满足这个条件。

学习率的调整式:
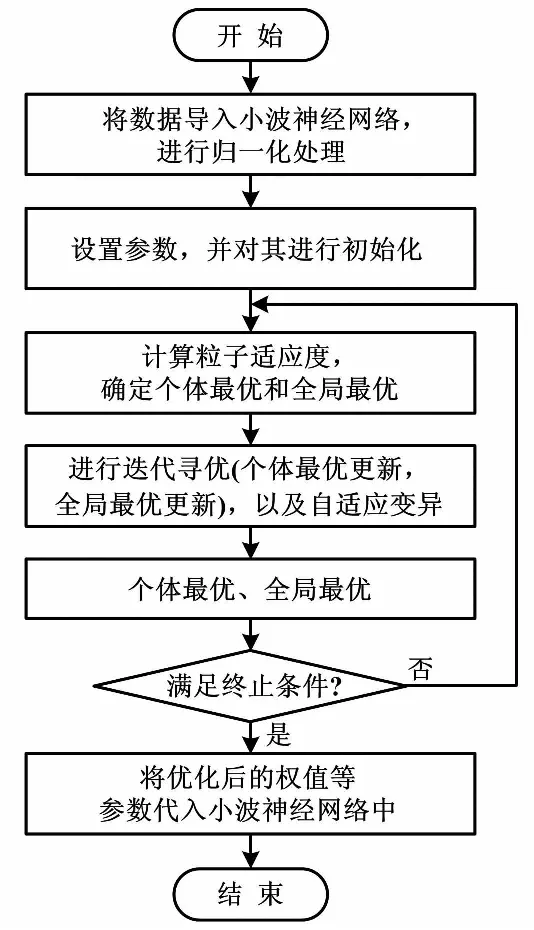
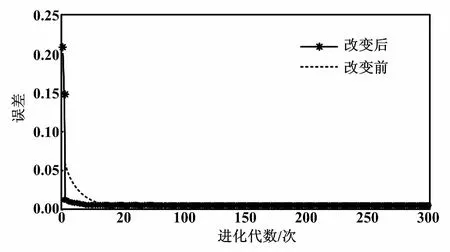
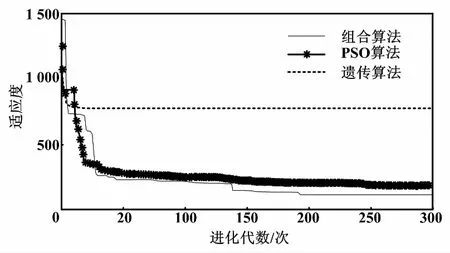
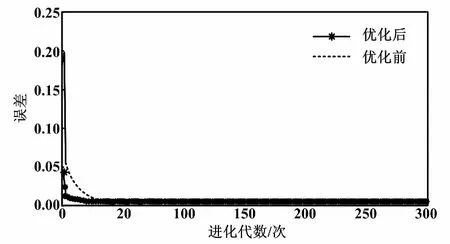
ηk+1=ηklog(1+k)e(k+1) (13) ηk+1=ηklog(2+1/k)e(k+1)≥e(k) (14) 式中:η为学习因子;λ为动量因子。 改进的小波神经网络训练算法,一定程度上加快了小波神经网络的收敛速度。但它仍然较易陷入局部最小,这无疑会对系统的收敛速度和精确度造成影响[13]。下面采用PSO与GA的组合算法来对小波神经网络的权值和阈值进行修正,以进一步提升其性能。 1995年,美国的Kenney和Eeberhart对鸟类的群体行为进行探究,提出了PSO算法[11]。每个粒子都可以看作潜在的要解决的优化问题的解决方案。粒子的速度取决于它的飞行的距离及其方向,它的适应值由优化函数决定。在飞行过程中,粒子经过多次迭代后,利用自身和飞行经验组进行动态调整,最后取得最优解。粒子本身所得到的最佳值可以称作个体的极值,而整个种群的最优解应是当前的极值。这一极值会在每个粒子寻找这两个最佳值时更新: vk+1=c0+vkc1(pbestk-xk)+c2(gbestk-xk) (15) xk+1=xk+vk+1 (16) 式中:vk为粒子的速度矢量;xk为目前粒子所在的位置;c0一般取介于(0,1)之间的随机常数,通常可以称为惯性系数或收缩因子。采用c1和c2的“自感知因子”和“社会认知因子”来调节pbestk和gbestk对粒子的影响。 GA的本质是构建一个针对优化问题的目标函数的适合度函数[12]。然后,根据一定的规则,生成遗传密码的初始组,并对该组进行评估,进行遗传算法的交叉、变异、选择等。 遗传算法可以在不使算法变复杂的同时,提高算法的全局极值,从而提高算法的收敛速度和精度。在这种情况下,两者优势互补。它们的融合可以在提升学习速度的同时,增强系统的泛化能力。 PSO优化小波神经网络流程如图4所示。 图4 PSO优化小波神经网络流程图 对所提算法进行仿真,试验数据来自哈尔滨西至长春运营线路的实测数据,列车最高时速为200 km/h,平均车速为99.90 km/h[14]。设置北斗卫星接收机数据采样频率为1 s/次,哈尔滨西站的坐标作为初始位置的经纬度坐标,共收集了400个北斗Ⅱ卫星的测量数据(列车实际运行13.286 km)。为了便于分析,只采用了部分数据点进行仿真分析,并经由传统的卡尔曼滤波获得输出波形及数据。 在试验1中,小波神经网络采用并行输入[15],输入和输出的节点数都为1,是3层神经网络。其中隐层节点数为12,输出层节点数为5。如果对数据分块太多,则运行时间过长;如果数据分块太少,则会使误差偏大,所以将输入数据分成了4块。运行时间及均方差对比如表1所示。学习率改变前后误差曲线如图5所示。 表1 运行时间及均方差对比 图5 学习率改变前后误差曲线 在试验2中,遗传代数选择了300代,种群规模选择了50,变异率为0.95。算法适应度曲线如图6所示。从图6可以看出,组合算法在收敛速度上优于粒子群算法,且远远优于遗传算法。 图6 算法适应度曲线 在试验3中,采用了北向的数据集,对基于GA改进的PSO权值部分进行训练。当精度达到要求后结束训练,进入在线状态。在MATLAB 2015B中运行程序,对WNN辅助的卡尔曼滤波器所获得的速度曲线和原来实际运行的曲线,以及它们的误差曲线进行比较。优化前后误差曲线、总体误差对比曲线如图7、图8所示。 图7 优化前后误差对比曲线 从图7、图8可以看出,与实际运动曲线相比,经过改进的小波神经网络辅助的卡尔曼滤波,对于速度的估计误差更小,而且经过长时间的运行,偏差仍然不大,表明了通过小波神经网络对卡尔曼滤波器辅助的方法是可行的。经过PSO优化后的神经网络具有运行稳定且误差小和收敛快等优点。在PSO优化数据后,相比优化前WNN 中100个输出数据与理想输出之差有所减少,整体的均方差也由原来的0.150 5降低到了0.019 4。 本文提出了一种采用WNN对实际问题中的卡尔曼滤波进行建模的方案。在此基础上,对GA和PSO进行了组合优化。学习率则是通过加入对数函数进行改进。仿真表明,改进后的系统不仅加快了运行速度,而且减小了均方差。小波神经网络优化不但提高了收敛速度,还有效提高了其定位的准确性,同时在保持原速度波形的整体趋势前提下,减少了滤波导致的信号误差。在今后工作中,考虑在BDS/INS惯性导航系统失效的情况下,利用神经网络和其他算法融合进行运行路线的预测。 [1] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理 [M].2版.西安:西北工业大学出版社,2012. [2] 韩晓捷,陈德巧.基于神经网络酌高速列车位置计算模型在线学习算法设计[D].北京:北京交通大学,2016. [3] 周璐,郭超,钟颖,等.小波网络辅助卡尔曼滤波的捷联惯导传递对准[J].计算机测量与控制,2015,24(32):2518-2520. [4] 张宇阳,蔡伯根.基于北斗/SINS融合的列车定位方法研究[D].北京:北京交通大学,2016. [5] 罗建军.组合导航原理及应用[M].西安:西北工业大学出版社,2012. [6] 李笠,王万良,徐新黎,等.基于网格排序的多目标粒子群优化算法[J],计算机研究与发展,2017,18(5):1012-1023. [7] 孟军,史贯丽.融合粒子群优化和遗传算法的基因调控网络构建[J].计算机应用,2016,811(11):2969-2973. [8] 徐泽远,伊国兴,魏振楠.MEMS - SINS / GPS 组合导航系统设计[J].自动化仪表,2016,37(12):67-70. [9] 范广坡,余学飞,卢广文,等.改进PSO-BP算法的压力导丝温度及非线性补偿研究[J].自动化仪表,2016,37(10):12-16. [10]周敏,刘健,杨林,等.一种自适应卡尔曼滤波在动态导航定位中的应用[J].自动化仪表,2016,37(8):1-4. [11]黄杰,李军,郭翔.递推SOM神经网络在短时交通流预测中的应用[J].自动化仪表,2015,36(4):1-5. [12]HU Z T,YUAN G Y,HU Y M.Training method of neural network based on cubature kalman filter[J].Control and Decision,2016,31(2):355-360. [13]SISWANTORO J,PRABUWONO A S,ABDULLAH A.Linear model based on kalman filter for improving neural network classification performance[J].Expert System with Application,2016,49(15):112-122. [14]李卫东,贾洪明,冯祥雨.基于扩展卡尔曼滤波的列车定位[J].大连交通大学学报,2015(6):102-103. [15]GU R H,BANERJEE A.Self-sensing SMA actuator using extended kalman filter and artificial neural network[J].Procedia,Engineering,2016,144(20):629-634.3 粒子群优化算法优化的小波神经网络
4 仿真分析

5 结束语
