装配偏差分析在阀门研制过程中的应用
2018-01-18
(上海航天设备制造总厂,上海 200245)
0 引言
当前在产品研制过程中,极值法、统计分析法和蒙特卡罗法是分析装配偏差的三种常用方法[1]。极值法设定形成装配体的零件均以极值尺寸装配,而各零件均以极值状态装配为极小概率事件,与产品研制的实际情形相差甚远;统计分析法根据零件误差分布、利用二阶矩确定装配误差的总体分布,可有效分析一维装配误差和二维刚体装配问题中的简单案例;蒙特卡罗法采用随机数及零件装配函数分析装配偏差,是目前最完善、工程应用最广泛的分析方法。
蒙特卡罗法根据概率分布函数π(x)产生随机(伪随机)样本,具有巨大的抽样效率以及与样本空间维数无关的计算精度,广泛应用于工程、材料、计算机、化学、生物、物理、统计以及经济与金融等学科[2]。目前,基于蒙特卡罗算法的装配偏差分析技术已经应用于汽车车身的尺寸与几何公差的设计[3]。
阀门是运载火箭中的关键附件,分布在加注、控制、增压等环节中,在火箭加注和飞行过程中分别起着加注安全、稳定贮箱压力和保证介质稳定输送的重要作用。阀门一旦失灵,其后果将是灾难性的,因此高可靠性成为对运载阀门的基本要求。影响阀门达到上述要求的因素分布在设计、零件制造、装配、测量环节中,最终集中反映到阀门关键特性的装配偏差中。
目前对于影响阀门关键特性的因素及其相互之间的作用关系缺乏系统性的分析工具与方法。在阀门装配阶段主要通过试装选配获得要求的关键特性值,在当前较大批量生产的背景下,迫切需要在研制方法上有所突破。本文针对具有螺钉调整关键特性结构的阀门,采用基于蒙特卡罗法的装配偏差分析技术对阀门装配时使用不同参数的调整垫片以及不同的螺钉调整位置的情形下的关键特性进行分析,识别出影响关键特性的关键尺寸与几何公差,以及满足关键特性要求的调整垫片参数与螺钉调整范围,根据该垫片参数与螺钉调整范围进行装配实验,并将分析数据与实验数据进行比对。
1 基本原理与方法
1.1 工艺能力
在产品设计时,对零件特征的尺寸与几何公差的上偏差USL(Upper Specification Limit)和下偏差LSL(Lower Specification Limit)进行限定,形成尺寸与几何公差的设计范围USL-LSL。在零件的制造过程中,尺寸与几何公差表现出随机性,这种随机性一般可用正态分布描述,用6表示尺寸与几何公差在制造过程中的分布范围,如图1所示。
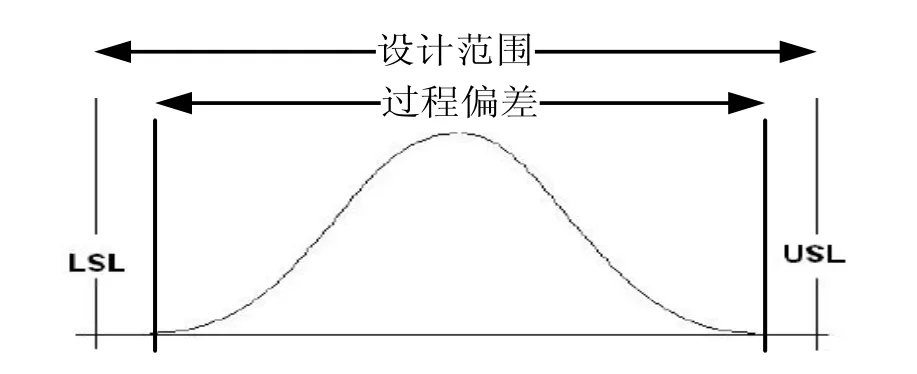
图1 工艺能力
定义工艺能力指数Cp表达式为式(1),该式表征了尺寸与几何公差设计范围宽度与制造分布范围宽度的匹配程度;定义工艺表现指数Cpk表达式为式(2),该式表征了尺寸与几何公差设计范围中间值与制造分布范围均值的匹配程度[4]。现代企业要求1<Cp<1.6,Cpk>1.33。

1.2 正态分布
根据概率论与数理统计理论,正态分布的以下两个性质对装配偏差分析具有重要作用:
性质1:正态输入总会产生正态输出。
性质2:设服从正态分布的随机变量为X,均值为µ,标准差为σ,现有常量C,则随机变量X+C或X-C服从正态分布,且均值相应为µ+c或µ−c,标准差为σ。
1.3 装配偏差分析流程
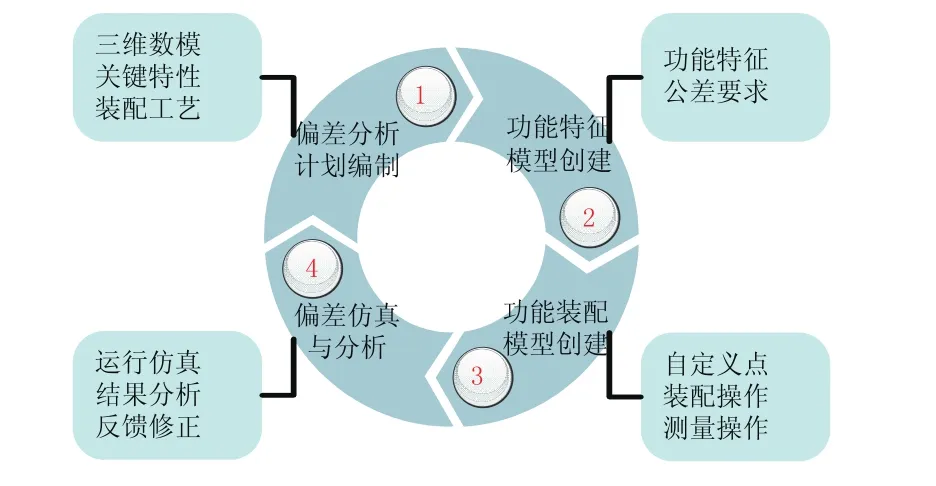
图2 装配偏差分析基本流程
基于软件Variation Analysis的装配偏差分析流程主要包含四个部分[4]:偏差分析计划编制、功能特征模型创建、功能装配模型创建、偏差仿真与分析,如图2所示。在偏差分析计划编制阶段,建立产品的三维CAD零件及装配模型,并将其轻量化为中间格式的JT模型,明确要分析的关键特性及其测量方案,以及装配工艺方案,包括装配顺序、装夹定位等方案。在功能特征模型创建阶段,分析影响关键特性的零件及其特征,并针对特征设定尺寸与几何公差。在功能装配模型创建阶段,将定义的零件特征在创建的装配操作中形成装配关系,并设定装配操作参数,装夹定位的约束按相同方式处理。
最后进行偏差仿真与分析,根据仿真得到关键特性的Cp和Cpk值,调整零件特征的尺寸与几何公差值(仅针对新产品设计阶段)以及装配工艺后,重新进行仿真分析,如此持续迭代分析,直至关键特性的Cp和Cpk值满足要求。
2 运载阀门装配偏差分析
2.1 分析问题描述

图3 某型阀门关键特性示意图
如图3所示为某型阀门的结构示意图,其关键特性为活门与壳体之间形成的开口间隙值,该值的大小控制着阀门出口的气体压力大小。设计要求在阀门装配完成之后间隙值的范围为0.8~1.2mm。针对该型阀门,影响间隙值的主要可能因素有零件设计尺寸与几何公差值及其在制造过程中表现出的随机性、垫圈-20的厚度(设计有0.5、0.8、1.0mm共3种规格可选)、调整螺钉-13的调整量。
2.2 偏差分析计划
在Pro/ENGINEER中创建阀门的零件及装配模型,利用JT Translator for Pro/ENGINEER将阀门装配模型转化为轻量化的JT模型。JT模型以三角面片表达零件的表面,与原始CAD模型相比,其数据量更小,适合于表达大装配体,同时JT模型是Variation Analysis进行偏差分析的标准输入模型格式。在装配阶段,经对装配工艺进行分析,影响间隙值的零件及其装配序列为:壳体-6、硬心-12、膜片-10、垫片-20、螺母-9、螺钉-13、螺母-23、活门-7。
2.3 功能特征模型创建
Variation Analysis将零件形成装配关系的特征总结为销、孔、平面、一般曲面、点、槽、凸台共7类功能特征,该特征直接基于零件的JT模型创建。零件之间由这7类功能特征中的1个或多个形成装配关系,每类功能特征可以指定相应的尺寸与几何公差,包括没有在设计文件标注出的重要一般尺寸公差,并设其在制造过程中服从正态分布。对影响间隙值形成的零件特征逐一分析,以壳体为例,其功能特征如表1所示,并且每一项功能特征与三维JT模型进行关联。
2.4 功能装配模型创建
根据创建的功能特征模型,定义零件之间的装配操作,一个装配操作由多个装配关系构成,其中装配关系由零件功能特征相互之间匹配形成,设定零件之间的装配类型为标准,即为刚性装配。以零件活门为例,其装配操作定义如表2所示,活门的销-2、销_3特征与壳体的孔_2特征匹配,参数选择Float表示销会随着孔及其自身的设定公差浮动;活门的球面顶端与螺钉的端面接触。
装配操作定义完成之后,对间隙值定义测量操作,如表3所示,测量类型为点到面,设定间隙值上偏差USL=1.2,下偏差LSL=0.8。
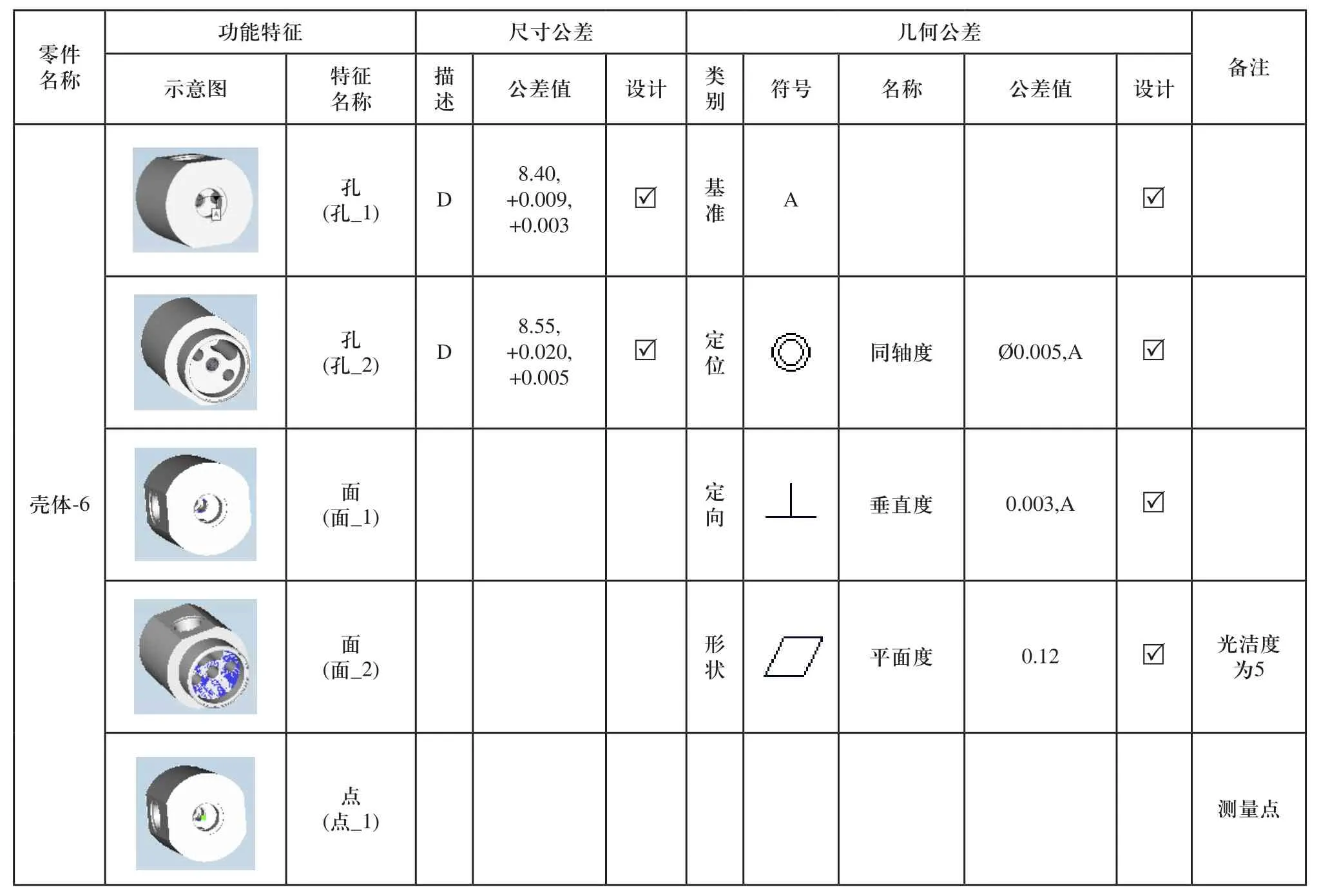
表1 零件壳体-6功能特征
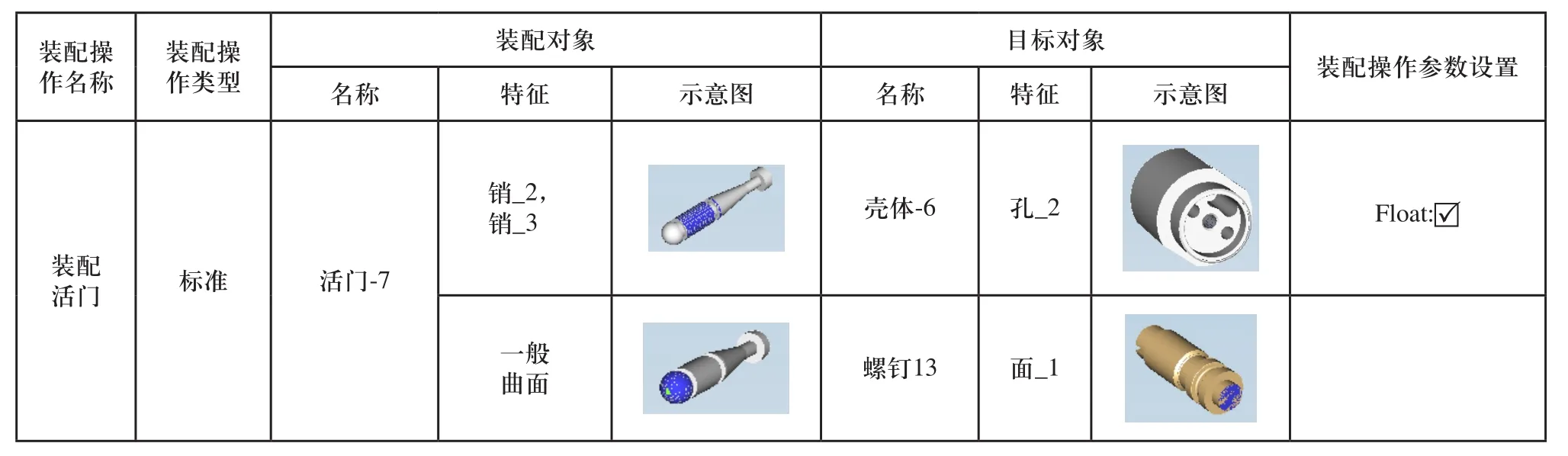
表2 零件活门-7装配操作

表3 阀门间隙值测量操作
2.5 阀门间隙值装配偏差仿真与分析
在完成偏差分析计划编制、功能特征模型创建、功能装配模型创建之后,进行间隙值的仿真与分析。定义仿真情景1:垫圈-20厚度0.5mm,调整螺钉-13左端面与螺母-9左端面平齐(方向定义以图3为参照,下同)。仿真次数设定为10000次,即使用蒙特卡罗法按正态分布产生10000个样本,模拟制造装配了10000套阀门。影响形成间隙值的零件的尺寸与几何公差为输入值,间隙值为输出值,按1.2节所述正态分布的性质1,间隙值服从正态分布。间隙值的仿真分析结果如图4(a)所示。分别采用垫圈-20厚度为0.8mm、1mm两种规格,其余条件保持不变,间隙值的仿真分析结果如图4(b)、图5(a)所示。
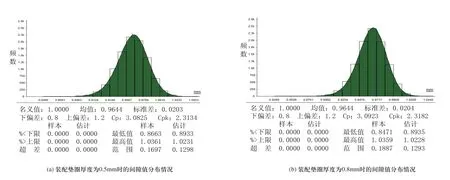
图4 间隙值分布情况
从图中数据可以看到,分别采用3种规格的垫圈对间隙值分布的均值和标准差的影响极小,因而可得出垫圈的厚度对该型阀门间隙值的影响可忽略不计。同时,间隙值均在设计范围之内,但是Cp和Cpk值偏大。Cp>1.6即为极高工艺匹配能力,即USL-LSL>9.6σ,样本值落在区间的概率在99.9937%(8σ)与99.999943%(10σ)之间。

图5 间隙值分布情况
以选用垫圈厚度为1mm时的仿真结果数据为例,Cp=3.0237,即USL-LSL=18.1422σ。说明存在以下问题:1)USL-LSL过大;2)σ过小。问题1)表明了允许间隙值变动的范围偏大,在实现产品功能的前提下,可适当缩小USL-LSL值,可降低Cp值。
问题2)反映了装配形成间隙值的零件尺寸与几何公差限制过严,导致加工经济性降低。为了调整间隙值分布范围,依据表4所示的贡献因素分析表(本表仅包含作了调整的因素),按照贡献率的大小对相应零件特征的尺寸与几何公差放大。贡献率越大的因素,对其进行调整(放大/缩小)对间隙值的影响也越大。调整后的间隙值分布情况如图5(b)所示,Cp=2.9250,与偏差因素未作调整前的Cp相比,值降低了3%左右,因而偏差分析为产品在设计阶段的零件尺寸与几何公差设计提供了有效的分析优化技术方法。
上述对尺寸与几何公差放大,验证了可通过该途径实现Cp值的调整。下文仍以初始的尺寸与几何公差的分析数据为分析依据。除了问题1)、2)影响因素外,螺钉的调整量直接影响到间隙值的大小。本文约定调整螺钉-13左端面与螺母-9左端面平齐为零点,向左调整为正值方向,向右调整为负值方向。在要求Cpk>1.33的情形下,求解螺钉调整量过程如下。
取σ=0.02,根据式:

解得,µ≤1.1202,根据式:

解得,µ≥0.8798。综上,可得间隙值的样本均值的范围0.8798≤µ≤1.1202。而间隙值名义值为1.0时,µ值为0.9645,对应调整螺钉调整量为0。可得在式(3)和式(4)约束下µ值的调整范围为-0.0847≤Δµ≤0.1557。而调整螺钉的调整量对应了间隙值的名义值的调整量,按1.2节所述正态分布的性质2,可推得调整螺钉调整量Δv的范围-0.0847≤Δµ≤0.1557。

表4 贡献因素尺寸与几何公差调整
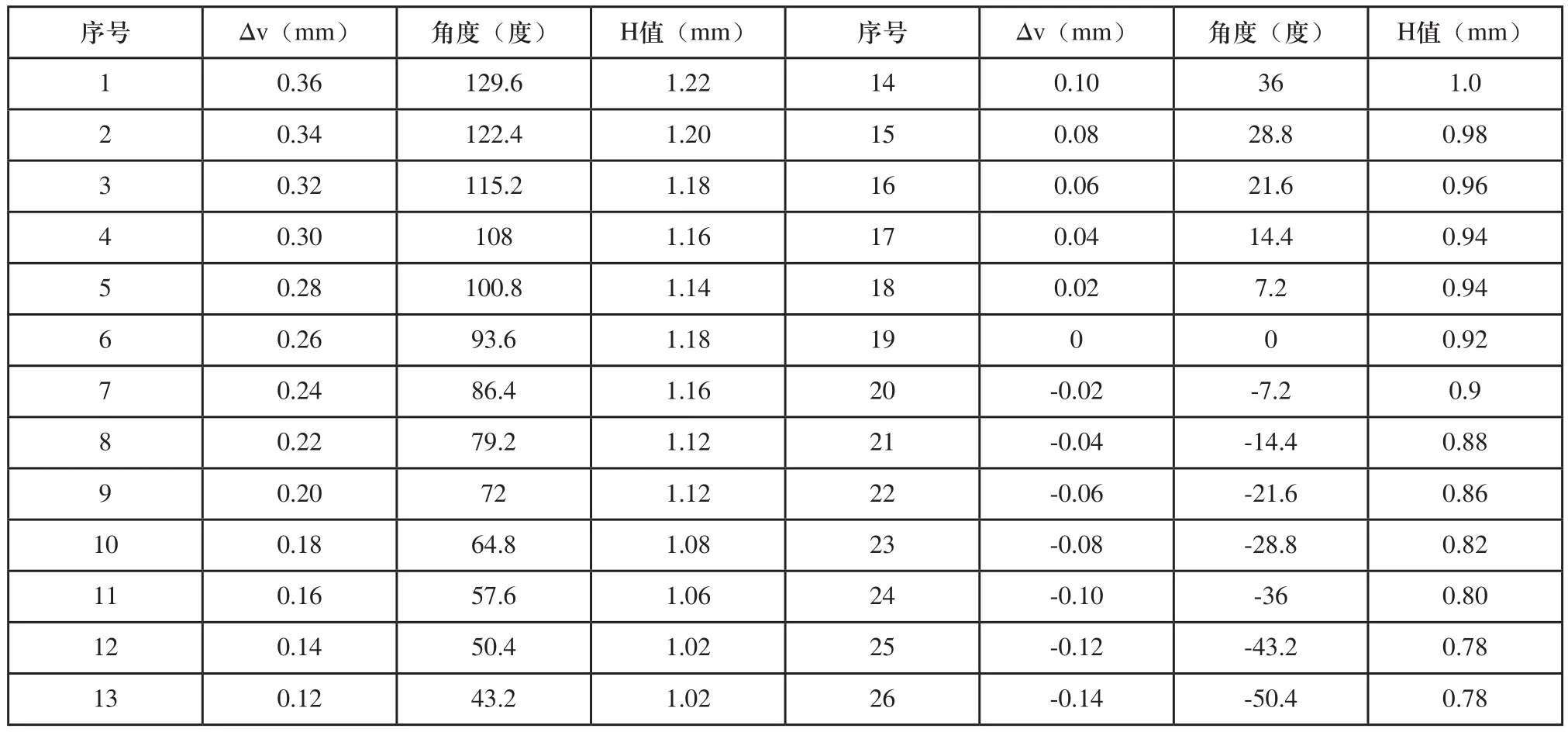
表5 实测数据记录表
以该型阀门典试件为验证对象,装配时选用厚度为1.0mm的垫圈,实测数据记录表如表5所示,其中∆v为螺钉调整量,角度为∆v值对应的螺钉拧动角度(螺纹为M8×1),H值为阀门的间隙值。从表5可知,当-0.0847≤Δµ≤0.1557时,0.86<H<1.06满足设计要求。因此,装配偏差仿真分析的结果与阀门实物研制装配的实测数据相一致。
综合上述分析过程,装配偏差分析在设计阶段提供了零件尺寸与几何公差优化设计的方法;在零部件制造阶段,根据分析的尺寸与几何公差对关键特性影响的重要程度对相应的零件的加工特征进行针对性的控制;在装配阶段,根据分析的量化调整范围直接调整关键特性的值,减少试装选配过程,提高装配效率。
3 结束语
本文以某型阀门产品为应用验证对象,对装配偏差分析技术进行了应用研究。结论表明装配偏差分析技术在产品零件制造、装配之前提供了一种零件尺寸与几何公差、零件制造及产品装配工艺方案分析与优化的技术手段。当前该项技术在汽车、飞机研制过程中得到了逐步应用,未来随着航天型号产品数字化研制工程的推进,将会在具有精密结构的航天型号产品的研制过程中发挥越来越重要的作用。
[1]林忠钦,等.轿车车体装配偏差研究方法综述[J].机械设计与研究,1999,(3).
[2]刘军.科学计算中的蒙特卡罗策略[M].高等教育出版社,2009.4.
[3]马振海,等.基于三维编差分析技术的尺寸公差设计与应用[J].产品与技术,2010,(5).
[4]MT9008 Variation Analysis(VSA) Version R8.1[M].Siemens,2009.11.
