平面简谐波垂直入射下锚固结构的动态响应

杨 博

(中车建设工程有限公司，北京 100078)

0 引 言

锚杆支护是一种结构简单的支护形式，经常与喷射混凝土、金属网等结合用于矿山、隧道和坝基等工程。在施工过程中，锚固结构除了受静载外，还受到爆破、采掘或地震等动载的影响。临近工作面的锚杆在经历不同频次动载后，会发生锚固力下降、锚固结构损伤破坏甚至失效的可能。

有关水电站工程和地下工程中爆炸应力波与锚固设施相互作用的研究表明：预应力对限制锚头松动和减小横向振动有利[1]；全锚树脂形式的顶板锚杆在距离爆破工作面3～4.6 m时，尾部比中部振动强烈，振动频率随着长度变化而变化[2]；临巷端锚锚杆距离掘进巷道6.4 m时，径向振动数值在同一量级上与轴向振动的变化类似，但是在持续时间方面径向振动较长[3]；测试隧道距爆破硐室净距为13 m时，锚杆的最大动应变在10-4量级，持续时间为15～20 ms[4-5]；与端锚锚杆相比，全锚的动态响应明显表现更强烈[6]。

本文通过弹性波在锚固结构中的衍射与反射作用研究爆破震动对树脂锚杆的影响，以期为地下硐室的动应力研究提供参考[7-10]。

1 应力波与锚固结构的相互作用

在传播过程中，如果应力波的传播距离超过柱状药包半径的5倍，则该问题可简化为平面波问题。

假设条件为：锚杆锚固在无限岩体中，a为锚杆杆体的半径，b为锚固体外半径；平面稳态P波沿垂直锚杆的轴线入射，入射波和坐标轴的方向如图1所示，P波的频率为ω，简谐变化，因此简化为平面应变问题。入射波表示为

(1)

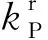
(2)

式中：λ和G为拉梅常数；E为弹性模量；μ为泊松比；ρ为介质密度。

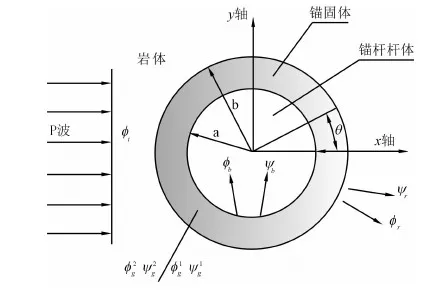
图1 锚固结构模型

1.1 锚固体中的波势函数

用圆柱波函数将入射波展开为无穷多个柱面驻波的叠加，表示为

(3)

式中：r为极径；θ为极角；Jn(y)为第一类Bessel函数；n=0时,en=1;n=1,2,3,…∞时,en=2。

P波传播到岩体与锚固体界面时，将发生反射和折射现象，反射为向岩体传播的P波、SV波和折射为向锚固体传播的P波和SV波，4种波函数分别表示为

(4)

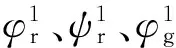
(5)

在锚固体与锚杆界面，P波发生反射和折射，反射向锚固体传播的P波和SV波和折射向锚杆传播的P波、SV波，折射进入锚杆体中的波函数须满足在r=0点处的有界性，折射波可表示为局限在锚杆中的驻波，它们的波势函数分别表示为

(6)

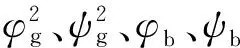
P波垂直入射时，岩体中总的波函数为

(7)

锚固层中总的波函数

(8)

锚杆中总的波函数

(9)

1.2锚固体中的应力和位移

柱面坐标的平面应变问题中应变、位移和波函数的关系为

(10)

(11)

式中:εz、εr、εθ和εrθ分别为轴向应变、径向应变、切向应变和剪应变；ur和uθ为径向位移和切向位移。

根据式(10)、(11)推导岩石、锚固体和锚杆3种介质中的位移和应力表达式，省略时间因子，岩石中的位移和应力为

(12)

(13)

锚固层中的位移和应力为

(14)

(15)

锚杆中的位移和应力为

(16)

(17)

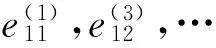
1.3 边界条件

依据连续介质紧密接触问题所提出的连续性条件，在接触面上2种介质的位移、径向正应力、剪应力均相等。

在r=b的连续条件为

(18)

在r=a的连续条件为

(19)

2 数值分析与讨论

在式(12)～(17)中令r取值为a、b，并利用边界条件，建立方程如下，依此求出各待定系数。

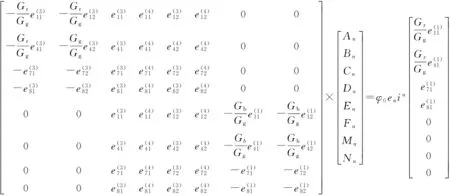
(20)

级数和形式的动应力可表示为(A+iB)e-iωt的复数形式，取其实部Acos(ωt)+Bsin(ωt)作为其应力解，峰值应力为(A2+B2)0.5。

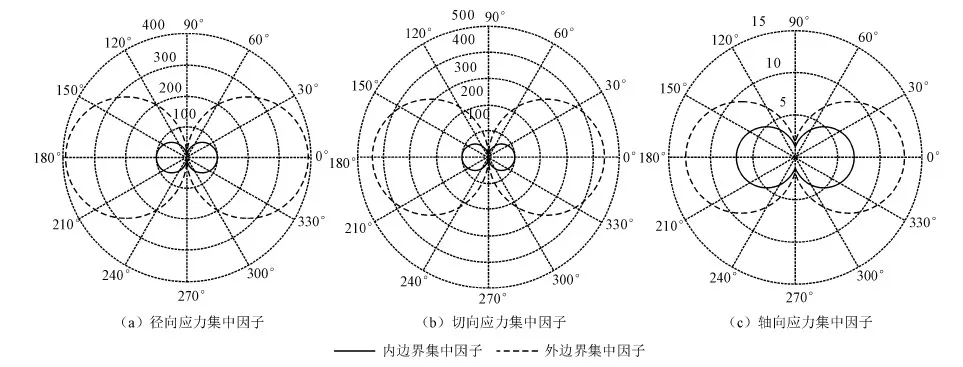
图2 200 kHz时锚固体边界上动应力的集中因子分布

介质中各种动应力可表示为无量纲的动应力集中因子

(21)

根据相关试验测试结果，爆破应力波对锚固结构的影响主要集中在离工作面较近的区域，爆破振动频率在100～4 000 Hz范围，根据频率范围设定算例研究应力波频率等对锚固的影响。

2.1 算例分析

设定岩石、树脂和锚杆的密度分别为2.6、2、7 g·cm-3，弹性模量分别为27.3、16、200 GPa，泊松比分别为0.25、0.3、0.25。

锚杆的半径为12 mm，锚固体外半径为18 mm，入射P波的频率为200 Hz时的动力响应如图2所示。

径向、切向和轴向正应力的峰值随锚杆的部位和时间变化而变化。图2显示200 kHz时3种正应力的峰值大小各异，但分布相似。切向应力最大，径向应力与切向应力的数值大小在同一量级；在数值大小上轴向应力峰值比切向应力和径向应力峰值约小1个量级。对于锚杆的一般部位来说，正应力在内边界的峰值比在外边界大1～4倍；峰值正应力在与入射波方向呈0°和180°的部位上最大；3种峰值正应力在与入射波方向呈90°和270°的部位最小。在此种边界、介质和入射条件下，应力分布类似水平荷载σ和竖直荷载ν(1-ν)σ作用的刚性加塞物的静力解。

理论假设入射波为简谐波，峰值应力的集中因子只表示力的大小，不能表示方向。实际上切向正应力和径向正应力虽然在同一位置达到最大值，但是性质是不同的，在同一时刻，一个为最大压应力，而另一个为最大拉应力。爆炸波在锚固结构中传播时引起锚杆结构的动力响应，当动应力超过介质的动态抗拉强度，容易在岩石-锚固体和锚杆杆体-锚固体两个界面上的0°和180°位置引起裂纹的产生和发展，从而造成锚固结构的损伤破坏。

2.2 频率的影响

爆破应力波的传播过程中，不同频率产生的影响不同：离工作面较近的锚固结构受到高频成分的影响较大，高频波作用下锚固结构振动幅值较大，易产生裂纹；随着距离增加，应力波逐渐衰减，如果其频率接近结构的固有频率，则会产生振动作用的放大。

应力表达式中各种函数都与无量纲波数k·r有关，入射频率小于1 kHz时，k·r值较小，各种参数的变化对应力影响小，且应力的大小主要由级数表达式的前几项决定。当k·r较大，波长逐渐减小至接近锚杆尺寸时，入射波在锚固结构中引起的应力分布将发生较大的变化。图3为1、4、6 kHz时轴向和径向动应力集中因子的分布。

通过数值计算可知，入射波频率大于1 kHz，即波长与锚固体直径的比值小于31后，轴向正应力的分布关于y轴逐渐不对称。随着频率的增大，这种不对称性愈加明显，集中因子在锚固体迎波侧较大且相邻部位数值大小相近，在背波侧较小且相邻部位数值差别明显，但背波侧θ=0°附近属于集中因子最大区域，尤其是在波长与锚固尺寸相近时比较明显。

径向正应力的集中因子分布和切向正应力的集中因子分布情况均会随着频率的增加发生变化，但由于两者的基础值较大，在1～4 000 Hz时分布的变化表现不明显。当频率大于4 000 Hz后，即波长与锚固体直径的比值小于7.8后，动应力集中因子分布明显变化，锚固体迎波侧和背波侧的集中因子分布异化；随着频率的增加，在外边界背波侧的集中因子明显偏大，在内边界迎波侧的集中因子明显偏大。

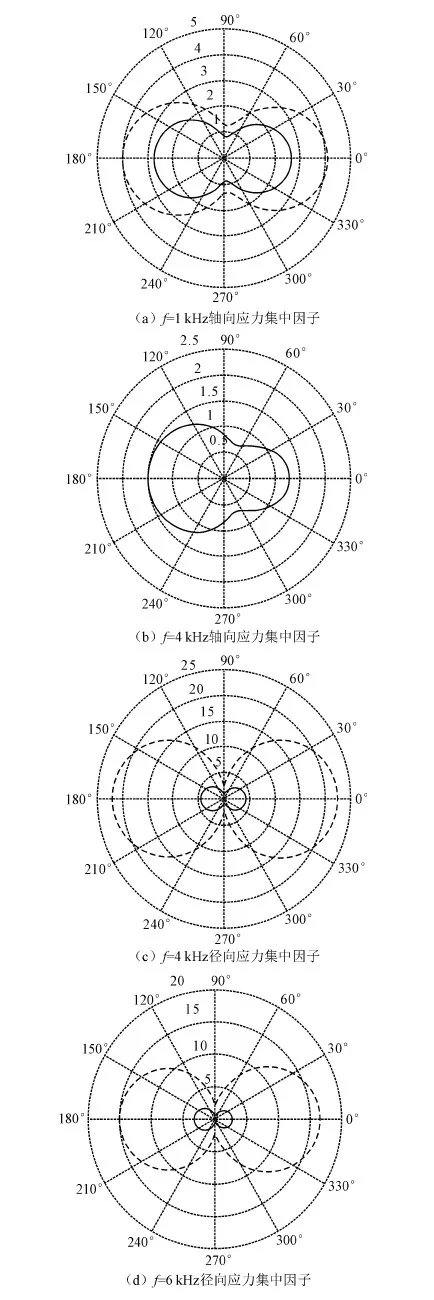
图3 1、4、6 kHz时边界上动应力集中因子

动应力集中因子表示在相同入射波频率的条件下各种动应力的无量纲比值。由动应力转换为动应力集中因子时因除去了包含频率的2次项，因此不能进行不同频率时集中因子的比较；图3显示动应力集中因子在高频时较小，实际上动应力是随着频率的增加而增加的。

当入射波频率较大且波长逐渐减小至接近锚杆尺寸时，应力峰值较入射波低频明显增加，锚固结构振动产生径向和轴向应力分布的明显不同，具有显著的不对称性，试验时近区锚固结构对称面爆破振动波形明显不同也从理论上得到了证明。

3 结 语

入射波频率小于1 kHz时，锚固体周围的应力分布类似于水平荷载σ和竖直荷载ν(1-ν)σ作用的刚性加塞物的静力解，径向正应力和切向正应力较大，轴向正应力最小，正应力最大位置是与入射波的夹角为0°和180°的界面。当入射波频率大于1 kHz且入射波波长接近锚固体几何尺寸时，其正应力集中因子的分布和低频入射波情况差异明显，锚固结构产生的动应力幅值明显增大，关于y轴的不对称性愈加明显，在内外边界上的正应力集中因子分布形式也逐渐异化，从理论上证明了近区锚固结构对称面动应力明显不同。

[1] 张 云，刘开运.近区爆破对锚固设施的影响研究[J].水利发电，1996(8):23-26.

[2] OTUONYE F O.Response of Grouted Roof Bolts to Blast Loading [J].Int.J.Rock Mech.Min.Sci.& Geomech.Abstr，1988，25(5)：345-349.

[3] TANNANT D D,BRUMMER R K,YI X.Rockbolt Behaviour Under Dynamic Loading:Field Tests and Modelling [J].Int.J.Rock Mech.Min.Sci.& Geomech.Abstr,1995,32(6):537-550.

[4] 易长平，卢文波.爆破振动对砂浆锚杆的影响研究[J].岩土力学，2006，27(8)：1312-1316.

[5] ZHOU Y,JESSEN A.Internal Separation Distances for Underground Explosives Storage in Hard Rock[J].Tunnelling and Underground Space Technology,2009(24):119-125.

[6] 单仁亮，周纪军，夏 宇，等.爆炸荷载下锚杆动态响应试验研究[J].爆破，2011,30(8):1540-1546.

[7] 周纪军，单仁亮，贾志欣，等.近区锚喷结构的爆破振动特性研究[J].岩土力学，2013，34(8):2225-2230.

[8] 王光勇，郭晓燕，王 超，等.在拱腰爆炸荷载作用下锚杆动态响应数值分析[J].爆破，2015,34(2):33-38.

[9] 梁建文，张 浩，LEE V W.地下双洞室在SV波入射下动力响应问题解析解[J].振动工程学报，2004，17(2)：132-140.

[10] 奚家米，杨更社，冯 钢.锚喷支护隧道围岩可靠度分析[J].筑路机械与施工机械化，2008，25(9)：68-70.