考虑土体结构性损伤的静压桩承载力及时效性研究

杨庆光，李毛毛，王国锋 ，谢 松

（1.湖南工业大学 土木工程学院，湖南 株洲 412007；2.中国水利水电第十四工程局有限公司，云南 昆明 650000）

1 研究背景

在土体地基中进行静压桩施工属于典型的小孔扩张问题[1]。静压桩施工使桩侧土体产生扰动及结构性损伤，导致桩侧土抗剪强度降低，超孔隙水压力上升[2]。根据研究[3]发现，静压桩沉桩结束后桩侧土中超孔隙水压力将逐渐消散，单桩承载力将逐渐提高，这种承载力随时间变化的效应即静压桩承载力的时效性。静压桩单桩承载力时效性问题已受到国内外众多学者的广泛关注，并通过试验手段和理论研究的方法，对该问题展开了深入研究。R.Skov等[4]通过对大量现场实测数据进行统计分析，提出了静压桩承载力增长关系式，并提供了不同土层的时效系数取值。P.J.Bullock等[5]在R.Skov等的研究基础上，为方便工程应用，进一步确定了时效系数的平均取值。王伟等[6]在现场实测的基础上，引入时间参数，得到了考虑固结效应的超孔隙水压力解，并推导了极限承载力的计算公式。蒋跃楠等[7]以静压桩施工实测资料为依据，着重分析了静压桩的终压力与单桩竖向承载力之间的相互关系，提出两者之间的相关性估算方法。胡琦等[8]根据静力触探结果，运用数理统计回归拟合方法，给出了单桩极限承载力随时间变化的预测公式。张明义等[9]基于实测结果研究发现，停压后静压桩的复压压力比停压前压力有较大幅度的提高，并在此基础上提出承载力极限值预测公式。此外，张忠苗[10]、寇海磊[11]、胡永强[12]等利用灰色理论、模型试验和光纤传感器技术等方法，就管桩的承载力、桩端阻力及桩侧摩阻力等，随休止时间的变化情况开展了深入的研究。对于静压桩承载力时效性的理论研究，目前主要采用的是将圆孔扩张理论与超孔隙水压力消散理论相结合的研究方法。费勤发等[13]根据圆孔扩张理论，从实测资料出发，回归了桩侧摩阻力随时间增长的计算公式，推导出桩侧摩阻力最大增长值的计算公式。王伟等[6]通过考虑沉桩对桩侧土体水平向扰动损伤，研究了三维超孔隙水压力的消散和桩土的固结规律，获得了估算考虑时间效应的单桩极限承载力的解析解。王家涛等[14]通过球孔扩张理论，计算出不同时期桩极限摩阻力和桩端阻力，得到了不同休止期的静压桩极限承载力，并通过现场试验结果得到了验证。

王伟等[6]只考虑了沉桩施工过程中的径向扰动损伤对静压桩贯入阻力的影响，并未考虑桩侧土中扰动沿深度的变化。本文在此基础上，结合张明义等[15]对沉桩引起的桩侧土竖向扰动规律的研究，同时考虑静压桩沉桩引起的桩侧土体径向和深度结构性损伤，对Tresca屈服准则进行修正，进一步对静压桩沉桩贯入阻力展开研究。此外，结合静压桩桩侧土体超孔隙水压力消散规律，对静压桩沉桩完成后复压压力与复压时间的关系展开研究。通过本文的研究以期能为完善小孔扩张理论，揭示沉桩挤土效应的工作机理和静压桩承载力的时效性提供参考。

2 静压沉桩的力学模型

为建立静压桩沉桩过程的力学模型，对静压桩极限扩孔压力、桩侧土体应力应变和超孔隙水压力分布规律等问题进行研究，并作如下假设：

1）静压桩沉桩扩孔满足球形孔扩张假设，球孔极限扩孔半径与桩径相同，计算简图如图1所示。

2）桩侧土体为均质各向同性的弹塑性体，服从Tresca屈服准则。

3）不考虑土体的剪胀现象，但考虑沉桩过程中土体扰动引起的土体结构性损伤。

4）沉桩前土中同一深度的初始应力相等。

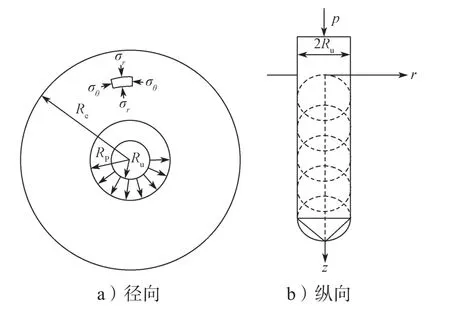
图1 球孔扩张力学模型Fig.1 A mechanical model of sphere cavity expansion

根据A.S.Vesic[1]球孔扩张的基本假设，满足如下平衡方程：

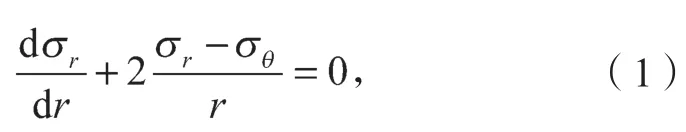
式中：σr为径向应力；σθ为法向应力。

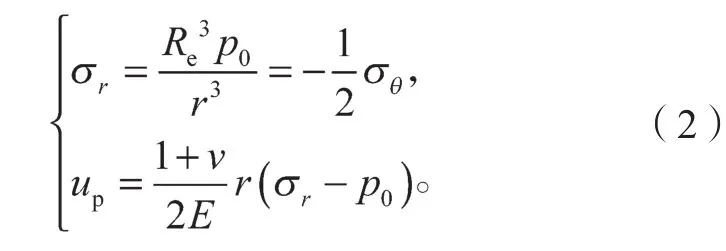
式中：Re为沉桩挤土效应影响边界距桩中心距离；

p0为土层初始应力，可以采用K0γz计算，其中K0为静止土压力系数，γ为土体容重；

up为桩侧土弹性区变形量；

E,v分别为土体弹性模量和泊松比。

根据假设条件可知，当桩侧土体进入塑性阶段后，满足Tresca屈服准则

式中τu为土体原位不排水抗剪强度。

静压桩沉桩时由于桩侧土体受到挤土效应的影响，产生不同程度的扰动，使土中超孔隙水压力上升，抗剪强度降低。因此，苗永红等[16]建议采用径向强度折减系数α1对扰动土体抗剪切强度进行折减。

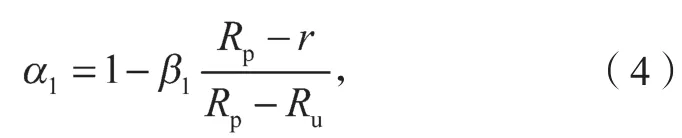
式中：β1为水平损伤系数；

Rp为桩侧土弹塑性交界面半径；

Ru为静压桩桩身半径。

由于式（4）仅考虑了沉桩过程中径向挠动对土体抗剪强度的影响，并未考虑沉桩过程中土体扰动沿深度变化情况。根据张明义等[15]的研究可知，静压沉桩过程中，桩侧土体沿深度方向可以分为松动区（L1）、滑动区（L2）和挤密区（L3），如图2所示。

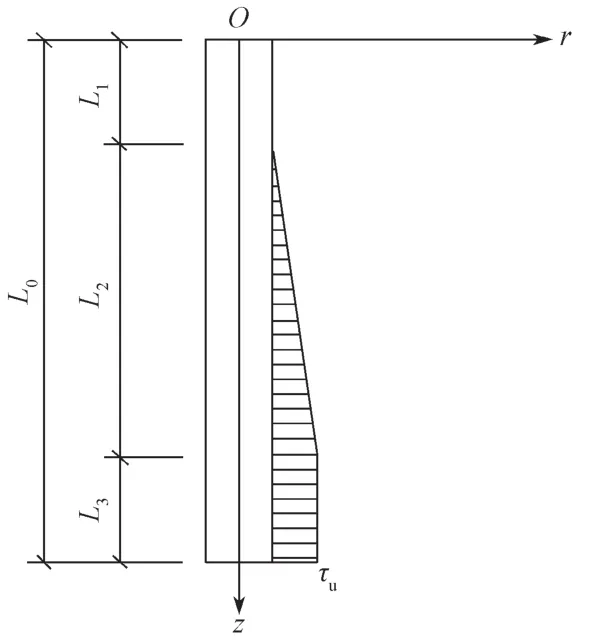
图2 桩侧土体摩阻力分布Fig.2 Distribution of the pile side soil friction

为充分考虑不同深度处沉桩引起的土体扰动差异，在式（4）的基础上，引入深度损伤系数β2来考虑扰动沿深度的变化规律，从而可以得到同时考虑桩侧土体径向和深度损伤的强度折减系数

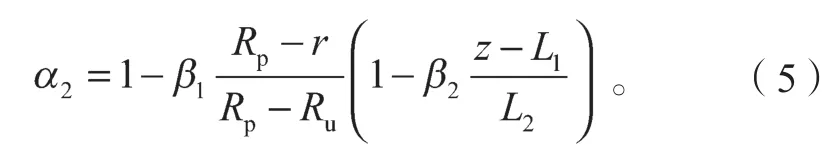
当z≤L1时，取z=L1；

当L1＜z≤L1+L2时，z按实际取值；

当L1+L2＜z≤L0时，取z=L1+L2。

从而修正后的Tresca屈服准则可以表示为

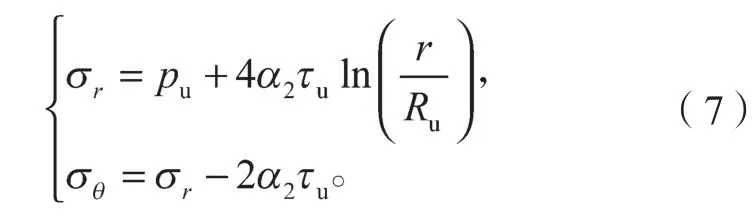
根据Tresca屈服准则可知，球孔扩张过程中塑性区体积应变为零，同时忽略塑性区范围内材料的弹性变形，则球孔扩张体积增大量与弹性区影响范围边界处体积变形量相等。假设静压桩施工前土中存在半径为R0的微小孔，从而有

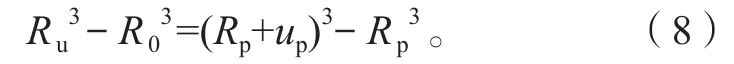
式（8）中，忽略R0和up的高阶项影响，可以得到

根据式（2）和式（6）可知，在弹塑性交界面位置上，有

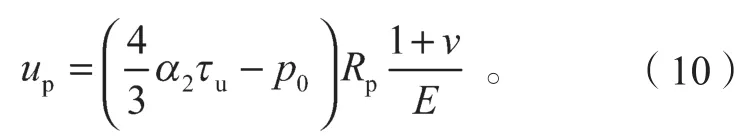
联立式（9）和式（10），有

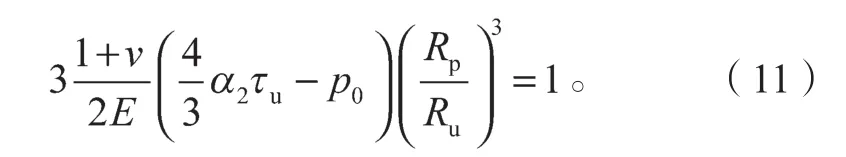
因此，当土层物理力学性质和桩身直径等参数已知时，由式（11）可以确定考虑土体径向和深度损伤情况下，弹塑性交界面半径Rp的取值，并进一步可以确定静压桩施工时极限扩孔压力为

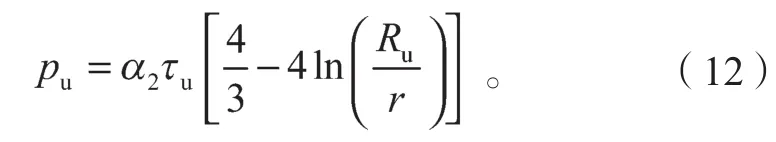
3 超孔隙水压力消散规律

根据研究[2,15]发现，在饱和土体中静压桩施工使桩侧土中产生较大的超孔隙水压力，并在桩土界面上出现一层自由水膜，降低了桩侧摩阻力的发挥。此外，由于沉桩施工使桩侧土产生一定的损伤扰动，桩侧土体中裂隙增加，有利于超孔隙水压力的消散。综上所述，可以采用图3所示的固结模型对静压桩沉桩结束后，桩侧土超孔隙水压力消散进行描述。

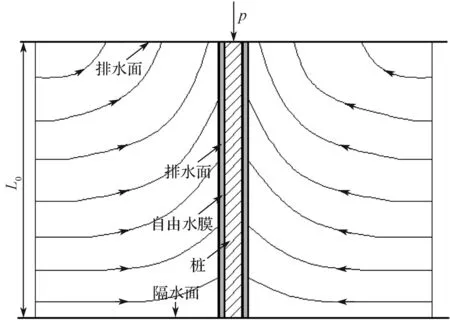
图3 桩侧土固结模型Fig.3 Consolidaton model of soil

文献[17]的研究结果表明，桩侧土中孔隙水压力消散引起的土体固结，由竖向固结和轴对称平面渗流两部分组成，并可以将桩侧土的固结度表示为

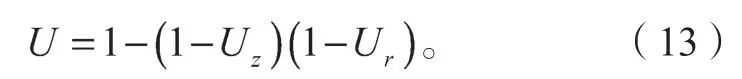
竖向固结度可表示为

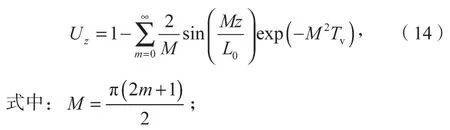
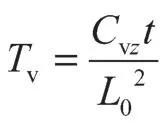
径向固结度可表示为

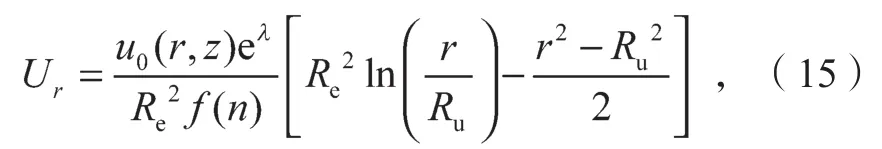
式中：u0(r,z)为沉桩施工完成瞬间桩侧土中初始孔隙水压力；

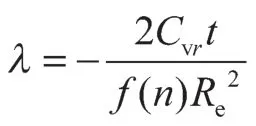
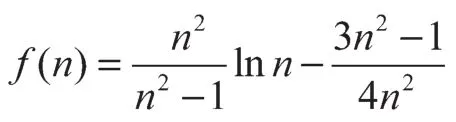
因此，为了确定静压沉桩施工完成后桩侧土体孔隙水压力的消散规律，还需要确定u0(r,z)的大小。根据Henkel公式[18]，并考虑土体结构性损伤，饱和黏性土中超孔隙水压力可以采用式（16）确定。

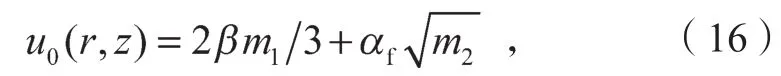
式中：β为Henkel孔隙水压力系数，对于饱和黏性土，通常取值为1；

m1,m2为换算系数，可以根据

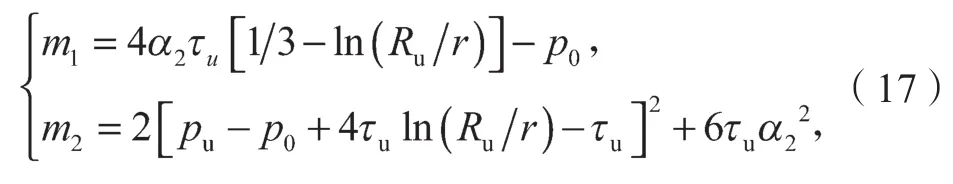
来确定；

αf为Skempton孔隙水压力参数，郑大同[18]建议采用

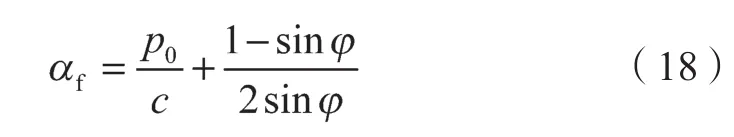
进行计算，其中c,φ分别为土体的黏聚力和有效内摩擦角。

4 静压桩承载力的确定

静压桩承载力由静压桩施工完成后的桩端阻力和桩侧摩阻力两部分构成。桩端阻力是由桩端穿透土层时受到土体抗力引起的，其取值可利用极限扩孔压力与桩端实际作用面积的乘积而得到。可以先计算不同深度处的极限扩孔压力，并考虑超孔隙水压力的消散，得到不同时刻有效扩孔压力作用下桩侧摩阻力的取值，并通过分段叠加的方法得到桩侧摩阻力的合力。将桩端阻力和桩侧摩阻力两部分叠加，即得到静压桩完全贯入土层后不同时刻承载力的取值。

当桩长为L0时，可以根据式（12）得到桩端极限扩孔压力，并求极限扩孔压力竖向分力的合力，从而得到入土深度为L0时刻桩端阻力的极限值

静压桩桩侧摩阻力的大小受桩侧压力的有效应力大小、桩土摩擦系数及桩土之间的黏滞作用影响。因此，根据文献[19]的研究，考虑超孔隙水压力的影响，结合式（13）～（15），可以得到桩侧摩阻力公式为

式中δ为桩土之间的摩擦角，可以采用室内剪切试验确定。

由于沉桩过程中，桩土接触面位置处土体的扰动十分明显，因此桩土侧摩阻力取值最终由式（21）来确定：

将桩长H均分为n等份（如图4），从而第i单元入土深度可表示为

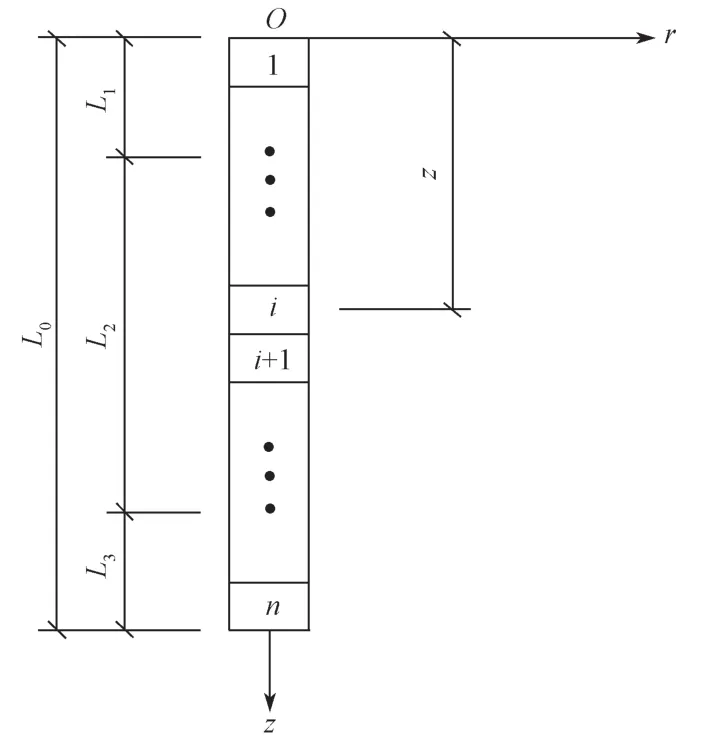
图4 桩身分段计算简图Fig.4 A sectional diagram for the calculation of the pile body

进一步可以得到桩侧摩阻力的合力为

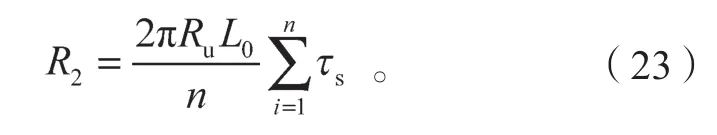
综上所述，将式（19）与式（23）计算结果进行叠加，可得到静压桩沉桩施工完成后，单桩承载力随时间变化的计算公式。

5 试验验证与对比分析

为验证本文所推导方法的可靠性，以某静压桩实际工程[14]中的2#单桩为例进行计算，并将计算结果与工程实测结果及其他理论值进行比较验证。实际工程中2#试验桩桩长为17 m，截面尺寸为350mm×350mm，等效直径为395mm，计算采用的参数如表1所示。

表1 土层参数表Table 1 Table of soil parameters

5.1 理论方法可靠性分析

图5为采用不同理论计算方法得到的不同休止期静压桩复压压力计算与实测曲线。从图5中的复压对比曲线可以看出，当静压桩完全贯入土层后，桩身复压压力计算值与实测值均呈现先急剧增大，然后逐渐趋于稳定的趋势，且吻合较好，这验证了本文计算方法的可靠性。

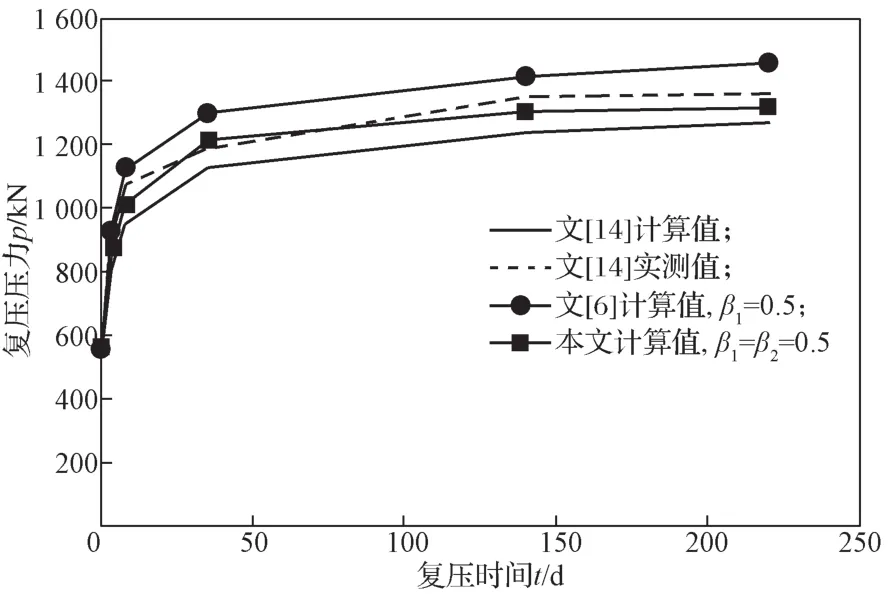
图5 不同方法下复压压力与时间的关系Fig.5 Relationship between the bearing capacity and the re-pressing time under different methods

表2为采用多种理论计算方法得到的不同休止期静压桩复压启动压力计算值与实测值。从表2所示对比结果可以看出，当β1和β2均取0.5时，采用本文方法得到的复压启动压力比文献[6]仅考虑径向土体损伤时复压计算结果偏小；而比文献[14]完全不考虑土体损伤影响的计算值总体偏大；并且采用本文方法得到的计算值与实测结果吻合度较上述2种理论计算方法的更高。这进一步说明，同时考虑径向及深度方向的土体扰动损伤差异，对于准确确定静压桩承载力和静压桩承载力与时间的关系十分必要。

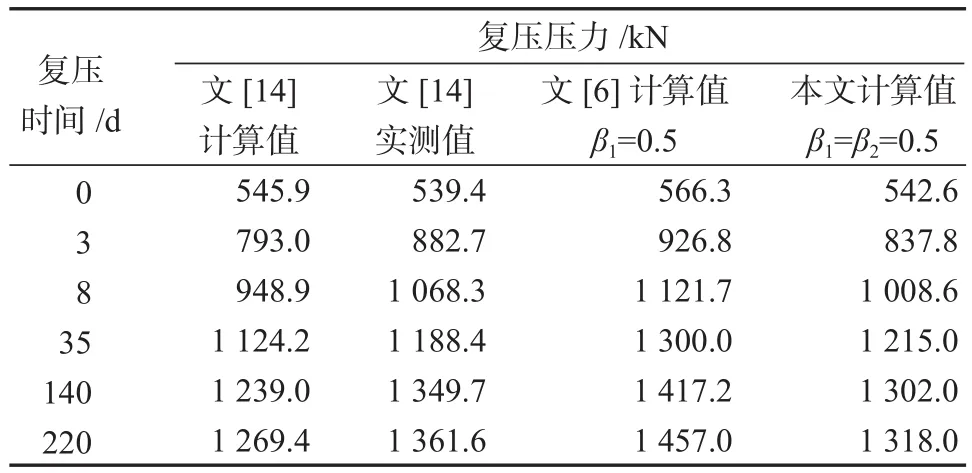
表2 不同方法下的复压压力Table 2 Figures of the re-pressing pressure under different methods

5.2 超孔隙水压力影响因素分析

图6给出了β1与β2取0.5时，2#桩桩侧深度8 m处，不同休止期内桩侧土中超孔隙水压力的计算值与距桩中心距离的关系曲线。从曲线可以看出，在距桩中心距3倍桩径左右的范围内，超孔隙水压力变化十分明显；超出该范围后，桩侧土中的超孔隙水压力较小，消散速度也更慢。这说明沉桩对桩侧土中超孔隙水的影响主要集中在距桩中心较近的范围内。此外，从图6曲线还可以看出，超孔隙水压力在休止初期消散较快，但是当休止期达到180 d后，超孔隙水压力基本趋于稳定，消散速度十分缓慢。

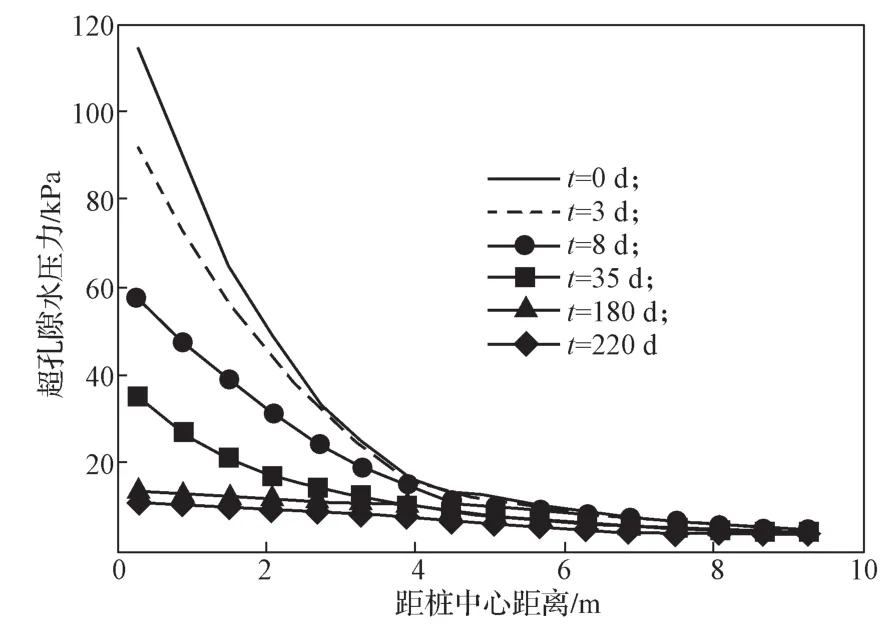
图6 超孔隙水压力与距桩中心距离的关系Fig.6 Relationship between the excess pore water pressure and the distance

图7给出了β1和β2取0.5时，不同休止期内桩侧壁位置处，超孔隙水压力计算值沿深度变化的关系曲线。从曲线可以看出，超孔隙水压力沿深度表现出明显递增的规律，休止期越长，孔隙水压力曲线越平缓。随休止期的增长，超孔隙水压力越小；深度越深，超孔隙水压力减少量越大。

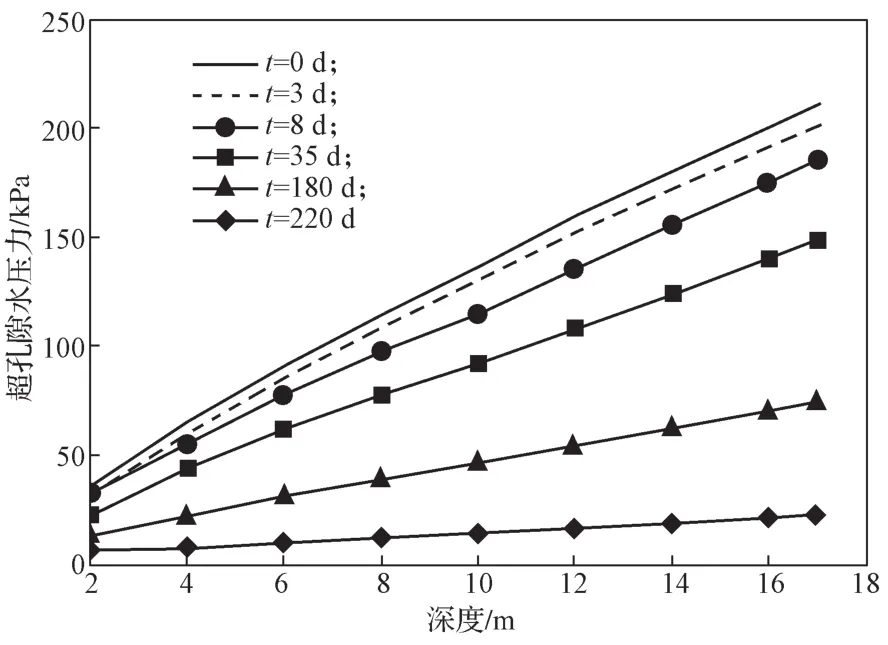
图7 不同复压时间下超孔隙水压力与深度的关系Fig.7 Relationship between the excess pore water pressure and the depth under difference re-pressing time

图8为静压桩复压时间t=0时刻，不同深度损伤系数下，桩侧壁位置处超孔隙水压力计算值沿深度变化的情况。从曲线可以看出，当径向损伤系数β1取0.5时，改变深度损伤系数β2的取值，超孔隙水压力计算值沿深度变化曲线略有差异。在相同深度位置处，β2值越大，超孔隙水压力计算值越大，且这种差异随着深度的增大逐渐增大。因此，考虑桩侧土体的竖向扰动损伤及正确地确定β2的取值，对于准确计算桩侧超孔隙水压力、沉桩贯入阻力及不同休止期的复压力大小，具有十分重要的工程意义。

图8 不同损伤系数下超孔隙水压力与深度的关系Fig.8 Relationship between the excess pore water pressure and the depth under different damage coef ficients

6 结论

综合上述研究可得如下结论：

1）同时考虑静压桩沉桩对桩侧土体径向和深度方向的扰动影响，采用本文推导得出的公式，计算静压桩承载力的计算结果，比仅考虑桩侧土体径向或完全不考虑桩侧土体扰动影响时的计算结果更接近于实测值，从而验证了本文计算方法的可靠性。

2）静压桩桩侧孔隙水压力的消散速度，受复压时间间隔和距离桩中心距离的影响明显。在距桩中心距离较近的一定范围内，孔隙水压力随离桩中心的距离的增加和复压间隔时间的增长，消散速率急剧下降，静压桩承载力越大；在此范围外，上述2个因素对超孔隙水压力消散速度的影响大幅降低。

3）当径向损伤系数β1已知，相同深度位置处，超孔隙水压力随着竖向损伤系数β2的增大而降低，且随着深度的增大，β2取值的大小对超孔隙水压力的影响更加明显。这充分说明了同时考虑桩侧土体的径向和深度扰动损伤，对研究静压桩的承载力及时效性十分重要。

[1]VESIC A S.Expansion of Cavity in Infinite Soil Mass[J].Primary Care，1973，33(1)：75-91.

[2]王 伟，卢廷浩，宰金珉，等.基于超静孔压消散的静压桩极限承载力研究[J].岩土力学，2005，26(11)：1845-1848.WANG Wei，LU Tinghao，ZAI Jinmin，et al.Study on Ultimate Bearing Capacity of Static Pressed Pile Based on Excess Pore Water Pressure Dissipation[J].Rock and Soil Mechanics，2005，26(11)：1845-1848.

[3]胡中雄.饱和软粘土中单桩承载力随时间的增长[J].岩土工程学报，1985，7(3)：58-61.HU Zhongxiong.The Increasing Bearing Capacity of the Single Pile with Time in Saturated Soft Soil[J].Chinese Journal of Geotechnical Engineering，1985，7(3)：58-61.

[4]SKOV R，DENVER H.Time Dependence of Bearing Capacity of Piles[C]//Proceedings of 3rd International Conference on the Application of Stress-Wave Theory to Piles.Ottawa：Bi-Tech Publisher，1988：879-888.

[5]BULLOCK P J，SCHMERTMANN J H，MICHAEL C.Side Shear Setup.Ⅱ： Results from Florida Test Piles[J].Journal of Geotechnical and Geoenvironmental Engineering，2005，131(3)：301-310.

[6]王 伟，宰金珉，王旭东.沉桩引起的三维超静孔隙水压力计算及其应用[J].岩土力学，2004，25(5)：774-777.WANG Wei，ZAI Jinmin，WANG Xudong.3D Calculation of Excess Pore Water Pressure Due to Driving Pile and Its Application[J].Rock and Soil Mechanics，2004，25(5)：774-777.

[7]蒋跃楠，韩选江.静压桩终压力及单桩竖向承载力的相关性[J].南京工业大学学报（自然科学版），2006，28(5)：63-66.JIANG Yuenan，HAN Xuanjiang.Relativity Between Final Pressure and Vertical Bearing Capacity of Static-Pressed Pile[J].Journal of Nanjing University of Technology（Natural Science Edition），2006，28(5)：63-66.

[8]胡 琦，蒋 军，严细水，等.回归法分析预应力管桩单桩极限承载力时效性[J].哈尔滨工业大学学报，2006，38(4)：602-605.HU Qi，JIANG Jun，YAN Xishui，et al.Regression Analysis of the Time Effect of Ultimate Bearing Capacity of Single Reinforced Pile[J].Journal of Harbin Institute of Technology，2006，38(4)：602-605.

[9]张明义，刘俊伟，于秀霞.饱和软黏土地基静压管桩承载力时间效应试验研究[J].岩土力学，2009，30(10)：3005-3008.ZHANG Mingyi，LIU Junwei，YU Xiuxia.Field Test Study of Time Effect on Ultimate Bearing Capacity of Jacked Pipe Pile in Soft Clay[J].Rock and Soil Mechanics，2009，30(10)：3005-3008.

[10]张忠苗，刘俊伟，俞 峰，等.静压管桩终压力与极限承载力的相关关系研究[J].岩土工程学报，2010，32(8)：1207-1213.ZHANG Zhongmiao，LIU Junwei，YU Feng，et al.Relationship Between Terminative Jacking Force and Ultimate Bearing Capacity of Jacked Pile Piles[J].Chinese Journal of Geotechnical Engineering，2010，32(8)：1207-1213.

[11]寇海磊，张明义，刘俊伟.基于光纤传感技术静压桩承载力时效性机理分析[J].岩土力学，2013，34(4)：1082-1088.KOU Hailei，ZHANG Mingyi，LIU Junwei.Bearing Capacity Efficiency Mechanism Analysis of Jacked Pile Based on Optical Fiber Sensing Technology[J].Rock and Soil Mechanics，2013，34(4)：1082-1088.

[12]胡永强，汤连生，黎志中.端承型静压桩沉桩贯入过程中桩侧阻力变化规律及其时效性试验研究[J].中山大学学报(自然科学版)，2015，54(1)：130-135.HU Yongqiang，TANG Liansheng，LI Zhizhong.Experimental Study on Variation and Time Effect of Shaft Resistance of Jacked Pile Installation[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2015，54(1)：130-135.

[13]费勤发，马海龙.饱和软土中排土桩桩侧摩阻力时效问题研究[J].苏州城建环保学院学报，1995，8(4)：35-40.FEI Qinfa，MA Hailong.An Analysis of Time Effectiveness of the Lateral Friction Growth Around Pile[J].Journal of Suzhou Institute of Urban Constructure and Environment Protection，1995，8(4)：35-40.

[14]王家涛，周 健，张明义.基于球孔扩张理论和时效性的静压桩承载力计算[J].地下空间与工程学报，2010，6(5)：964-968.WANG Jiatao，ZHOU Jian，ZHANG Mingyi.Computation of Bearing Capacity of Jacked Piles Based on Spherical Cavity Expansion Theory and Time Effect[J].Chinese Journal of Underground Space and Engineering，2010，6(5)：964-968.

[15]张明义，邓安福.桩-土滑动摩擦的试验研究[J].岩土力学，2002，23(2)：246-249.ZHANG Mingyi，DENG Anfu.Experimental Study on Sliding Friction Between Pile and Soil[J].Rock and Soil Mechanics，2002，23(2)：246-249

[16]苗永红，陈 邦.沉桩引起的初始超孔隙水压力理论解的修正[J].济南大学学报（自然科学版），2015，29(3)：185-189.MIAO Yonghong，CHEN Bang.Initial Excess Pore Water Pressure Caused by Pile Driving the Theoretical Solution of Correction[J].Journal of University of Jinan(Science and Technology)，2015，29(3)：185-189.

[17]HENKEL D J.The Shear Strength of Saturated Remolded Clays[C]//Research Conference on Shear Strength of Cohensive Soil.[S.l.]：ASCE，1960：533-560.

[18]郑大同.地基极限承载力的计算[M].北京：中国建筑工业出版社，1979：82-83.ZHENG Datong.Calculation of Ultimate Bearing Capacity of Foundation Soil[M].Beijing：China Architecture & Building Press，1979：82-83.

[19]杨庆光，刘 杰，何 杰，等.楔形与等截面静压桩沉桩贯入阻力对比研究[J].岩土工程学报，2013，35(5)：897-901.YANG Qingguang，LIU Jie，HE Jie，et al.Comparative Research on Penetration Resistance of Jacked Tapered Piles and Uniform Section Piles[J].Chinese Journal of Geotechnical Engineering，2013，35(5)：897-901.