柔性铰链放大的叠堆式超磁致伸缩致动器建模与实验

何忠波 荣 策 杨朝舒 薛光明 郑佳伟

(1.军械工程学院车辆与电气工程系， 石家庄 050003； 2.奥克兰大学机械工程系， 奥克兰 1010)

引言

超磁致伸缩材料(Giant magnetostrictive material, GMM)是一种性能优异的新型功能材料，相比于其他智能材料，GMM具有输出力大、响应速度快、能量密度高等优点[1-5]。超磁致伸缩致动器(Giant magnetostrictive actuator, GMA)能够在低电压驱动条件下迅速精确地输出微位移，被视为新型电液伺服阀(Electro-hydraulic servo valve, EHSV)的理想驱动元件[6-8]。

为避免GMM本身固有的倍频特性，在GMA设计时通常需要施加偏置磁场[9-10]。近年来，永磁偏置因低能耗和高可靠性的特点逐渐受到研究人员的关注[11-13]。在永磁偏置方式中，筒状永磁体磁场较为均匀，但所需永磁体的体积和质量较大[14-15]。碟片状永磁体常对称放置于GMM棒两端，这样的结构能以较少的永磁体获得较大的磁场强度，但是，磁场均匀性较差[16]。

本文根据新型EHSV的驱动要求，设计一种柔性铰链放大的叠堆式超磁致伸缩致动器(Stack giant magnetostrictive actuator amplified by flexure hinge, FASGMA)。为准确预测FASGMA的输出，建立FASGMA输出位移模型，模型考虑致动器与柔性铰链的相互作用以及GMM棒应变分布不均匀性，通过实验验证模型的准确性，有助于FASGMA整体性能的分析和在EHSV中的应用。

1 FASGMA结构与工作原理

FASGMA结构如图1所示，主要包括两部分：叠堆式超磁致伸缩致动器(SGMA)和桥式柔性铰链放大机构。SGMA采用永磁体、GMM棒交替排布的结构形式，既保留了两端对置式GMA质量、体积小的优点，同时提高了偏磁场分布的均匀性[17]。桥式柔性铰链机构结构紧凑，位移放大比大，能够满足大流量伺服阀的驱动要求[18-19]。两部分通过紧固螺钉相连，保证工作时能够同步运动。对于SGMA，可将其划分为5个功能模块。驱动模块由线圈和线圈骨架组成，为SGMA提供所需的驱动磁场。磁致伸缩模块由交替排布的GMM棒和永磁体组成，为SGMA提供偏置磁场。预压模块由外壳、左右端盖及碟簧组成，通过调整端盖与外壳之间的螺纹可以调节施加在GMM棒上的预紧力。冷却模块由冷却腔、进出液口以及密封圈组成，保证SGMA处于相对恒温的工作环境。输出模块主要由输出杆及相关附件组成，可以将GMM棒产生的应变转变为位移，并最终通过放大机构实现输出。

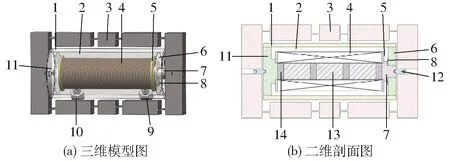
图1 FASGMA结构图Fig.1 Structure diagram of FASGMA1.外壳 2.冷却腔 3.桥式柔性铰链机构 4.线圈 5.线圈骨架 6.右端盖 7.输出杆 8.碟簧 9.出液口 10.进液口 11.左端盖 12.紧固螺钉 13.GMM棒 14.永磁体

2 SGMA应变分布模型

2.1 磁场模型

为准确描述SGMA磁场的不均匀性，将毕奥-萨伐尔定律与磁路模型结合，建立SGMA磁场分布模型，结果为

(1)

式中H(I,z)——GMM棒上坐标为z、驱动电流为I时的总磁场强度

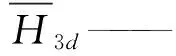
Ψb——偏置磁场的分布函数

Ψd——驱动磁场的分布函数

Ψb和Ψd利用毕奥-萨伐尔定律求得，在求解时，有两点需要考虑：①分布函数不应改变GMM棒上磁场强度的平均值。②分布函数应能反映高导磁材料对磁场的凝聚作用。Ψb和Ψd可最终表示为

(2)

式中Hb——毕奥-萨伐尔定律求得的GMM棒上偏置磁场分布

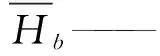
Hd——毕奥-萨伐尔定律求得的GMM棒上驱动磁场分布

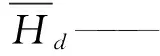
μr3——GMM棒的相对磁导率

β——与致动器结构相关的常数

2.2 磁化模型

SGMA的磁化模型可用Jiles-Atherton模型(J-A模型)描述为

(3)

式中H——驱动磁场强度

He——GMM棒中有效磁场强度

M——GMM棒的磁化强度

Man——无磁滞磁化强度

Mirr——不可逆磁化强度

Mrev——可逆磁化强度

Ms——饱和磁化强度

α——与分子场和预应力相关的磁化常数

k——钉扎系数a——形状系数

c——可逆系数

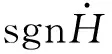
2.3 磁致伸缩模型

对于GMM，可以用二次畴转模型表示材料磁化强度与磁致伸缩应变之间的关系

(4)

式中λ——GMM棒的磁致伸缩应变

λs——饱和磁致伸缩应变

对于包含偏置磁场的致动器，GMM棒的实际应变应视为其围绕初始应变的往复运动。

3 放大机构输出建模

3.1 放大倍数计算

当FASGMA工作时，如果致动器沿水平方向伸长2Δx，相应地，放大机构将在竖直方向上升2Δy，放大比可表示为Δy/Δx。在分析机构放大比与结构尺寸的关系时，首先分析输入力FSGMA引起的左右支臂的变形，取左支臂进行受力分析，如图2所示。

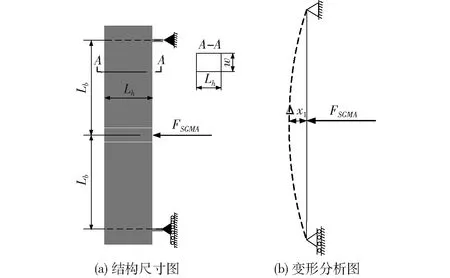
图2 左支臂受力分析图Fig.2 Force analysis of left support arm

令FSGMA=F1，则支臂中部的挠度为

(5)

式中E——放大机构弹性模量

Lb——支臂长度的一半

Ib——支臂惯性矩

在分析支臂的基础上，对柔性铰链和连接臂的组合结构进行受力和变形分析，选取放大机构左上部分，如图3所示，本文采用基于能量的分析方法[20]。

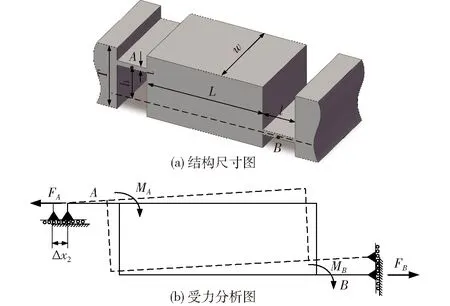
图3 柔性铰链及连接臂结构尺寸及受力分析图Fig.3 Structure and force analysis diagram of flexure hinge and link arm

在理想情况下，A、B两点的受力情况相同，转角也相等。假设FA=FB=F，MA=MB=Me，则Me=Fh。图3中，FA为该系统的输入力。由能量守恒，可得

(6)

式中 Δx2——柔性铰链及连接臂结构水平方向总伸长量

Δl——柔性铰链弹性伸长量

ΔL——连接臂弹性伸长量

Wf——柔性铰链弯曲应变能

Wc——连接臂弯曲应变能

通过受力分析可以看出，连接臂上所受的弯矩为0，所以弯曲应变能Wc也为0，Wf可以通过弹性梁理论解得，组合结构的轴向伸长可表示为

(7)

式中l——柔性铰链长度

L——连接臂长度

h——相邻柔性铰链间垂直距离

A1——柔性铰链的横截面积

A2——连接臂的横截面积

If——柔性铰链的惯性矩

柔性铰链放大机构在竖直方向上的位移可以视为柔性铰链和连接臂的挠度之和，即

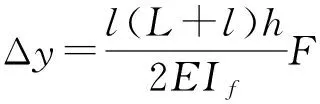
(8)

联立式(5)～(8)，柔性铰链放大机构的放大比Ramp可以表示为

(9)

3.2 固有频率计算

利用拉格朗日方程建立放大机构的动力学模型，可以计算其固有频率

(10)

式中D——放大机构动能与势能之差

Qk——第k个广义力

qk——第k个广义坐标

取放大机构的输入位移2Δx为广义坐标，用q表示。忽略柔性铰链的质量，放大机构的质量分布如图4所示。为避免对称结构的力和位移相互抵消，分析机构的左半部分。

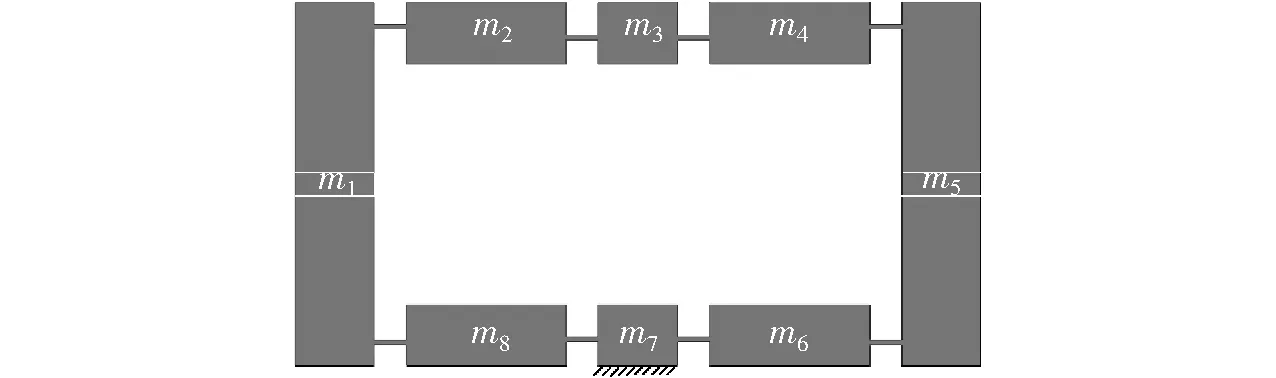
图4 放大机构质量分布图Fig.4 Mass distribution of amplifier

放大机构的动能包括机构各部分在x、y方向上的平动动能及柔性铰链旋转时的转动动能；而对于弹性势能，由于连接臂上弯矩为0，所以放大机构的弹性势能仅存在于柔性铰链上。将动能和势能代入拉格朗日方程表达式，可得

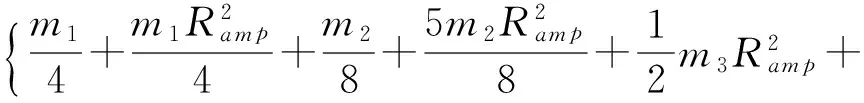
(11)

式中Kf——柔性铰链的转动刚度

Fout——SGMA的输出力

w——柔性铰链宽度

放大机构的固有频率可表示为

(12)

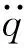
3.3 放大机构优化设计方法

3.3.1放大比影响因素分析

式(9)建立了放大机构位移放大比与各结构参数之间的关系，在放大机构结构尺寸确定的情况下，机构的放大比主要受柔性铰链厚度t、柔性铰链长度l以及柔性铰链间距h的影响，如图5所示。

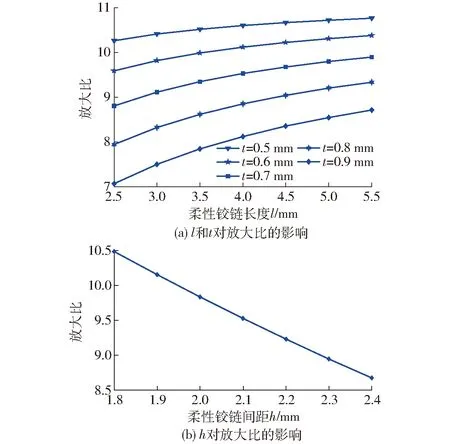
图5 放大机构结构参数对放大比的影响Fig.5 Influence of structural parameters on amplification ratio

可以看出，机构的放大比随l正向变化，随t和h反向变化。当需要较大的位移放大比时，应减小h和t，增大l。但是，这样会增加柔性铰链所受的正应力，加快材料的疲劳和损坏。

3.3.2固有频率影响因素分析

从式(11)、(12)可以看出，影响放大机构固有频率的参数主要包括柔性铰链厚度t和柔性铰链长度l，如图6所示。

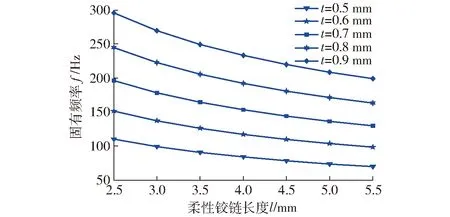
图6 放大机构结构参数对固有频率的影响Fig.6 Influence of structural parameters on eigenfrequency

由图6可知，增大柔性铰链厚度t，减小柔性铰链长度l有助于提高放大机构的固有频率，拓宽其工作频带。

3.3.3优化设计方法

从上面的分析可以发现，当t和l变化时，放大机构的放大倍数和固有频率变化趋势相反，无法同时达到期待的最优值。因此，在明确机构结构尺寸的基础上，需综合考虑t、l和h对放大机构特性的影响，最终确定参数取值，图7给出了这些参数优化设计的流程。

图7 放大机构优化设计流程图Fig.7 Flow chart of optimization design for amplifier

3.4 放大机构有限元分析

依据放大机构优化设计方法，确定了主要参数的取值，如表1所示。为验证机构计算模型的有效性，利用有限元软件对其进行放大比和固有频率分析。

表1 柔性铰链放大机构参数Tab.1 Parameters of flexure hinge mm

改变放大机构的输入位移，可得放大机构的输入-输出曲线，如图8所示。

图8 放大机构输入-输出特性曲线Fig.8 Input-output characteristics curve of amplifier

可以看出，放大机构的输入输出之间有较好的线性度，在输入位移0～20 μm的范围内，其放大倍数基本保持不变，约为9.208倍，而理论计算得到的结果为9.525倍，相对误差约为3.44%，说明模型有较高的计算精度。

利用有限元软件分析放大机构的固有频率，得到其前四阶模态如图9所示。

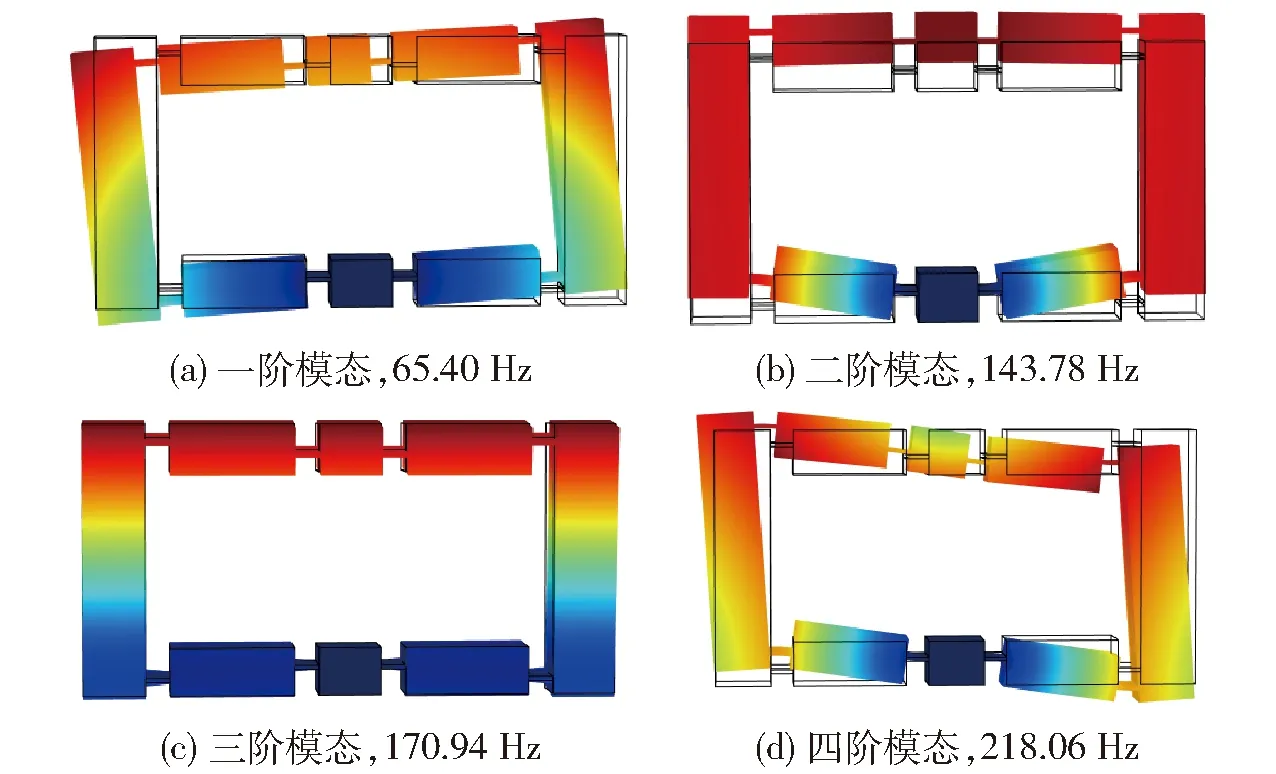
图9 放大机构前四阶模态图Fig.9 First four modals analyses of amplifier

从图9中可以看出，二阶振型为放大机构输出位移方向的变形，是放大机构工作时的主要变形形式。采用解析方法得到的固有频率应为二阶固有频率，计算值为153.24 Hz，有限元分析值为143.78 Hz，相对误差约为6.6%，表明放大机构的固有频率计算模型有较高的精度。

4 位移模型

考虑SGMA和放大机构的相互作用，建立能够反映FASGMA整体输出的位移模型。为描述SGMA磁场和应变分布的不均匀性，将每段GMM棒沿轴向划分为n个质量-弹簧-阻尼单元(n为任意正整数)，则整个致动器表示为如图10所示的多自由度振动系统。

以系统静平衡位置为坐标原点，该多自由度系统的运动微分方程为

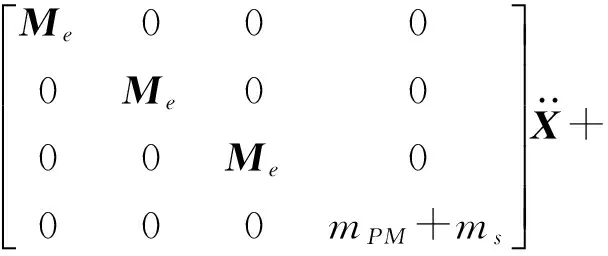
(13)

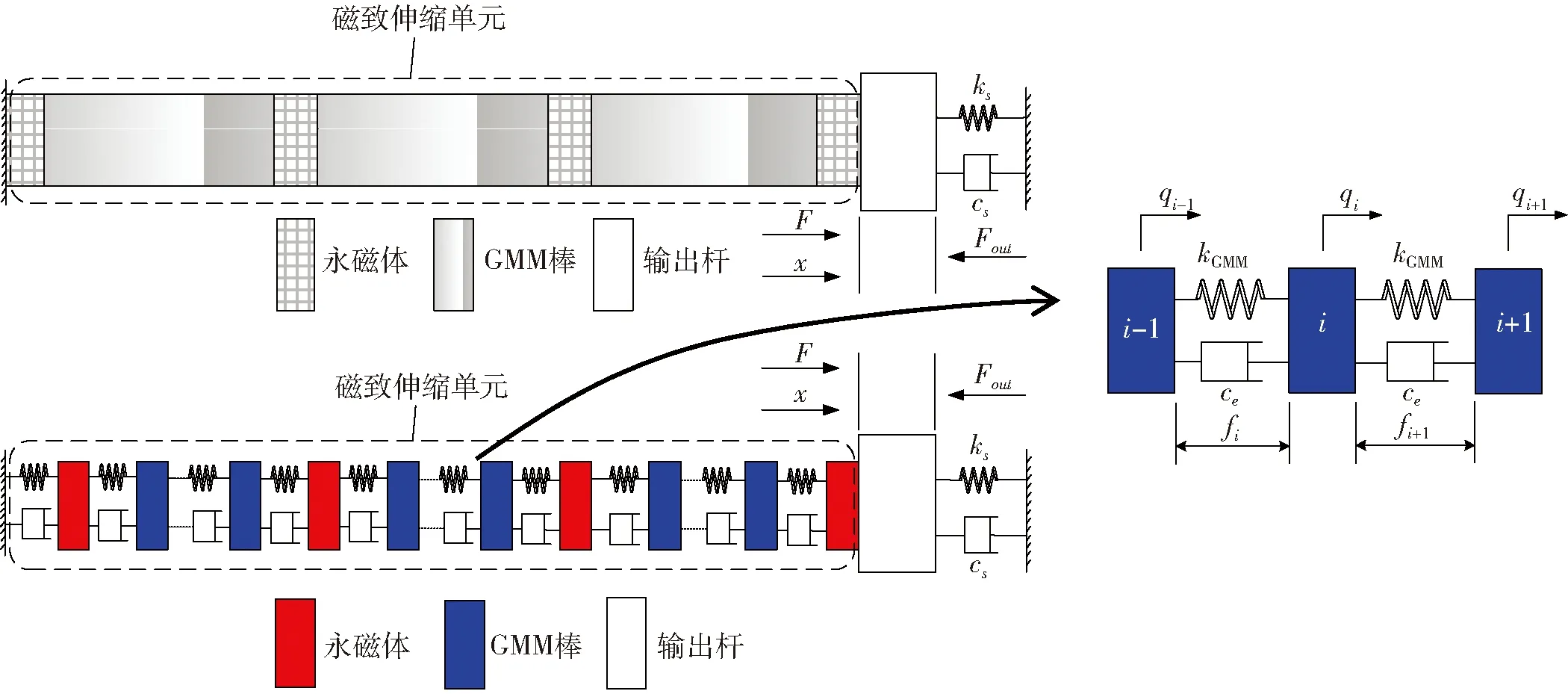
图10 SGMA位移模型等效图Fig.10 Equivalent diagram of displacement model for SGMA

其中

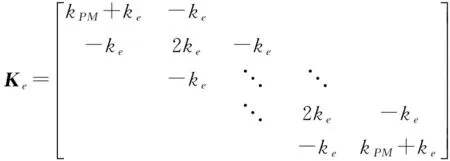
式中kPM——永磁体刚度

cPM——永磁体阻尼系数

ms——输出杆质量ks——碟簧刚度

mi——每段GMM棒中第i个质-弹-阻单元的等效质量

mPM——每段永磁体的等效质量

cs——输出杆与外壳之间阻尼系数

ke——GMM棒中任一质-弹-阻单元的刚度

ce——GMM棒中任一质-弹-阻单元的阻尼系数

X——SGMA的位移向量

将矩阵Ke中的相应元素换为cPM和ce，可得矩阵Ce。在磁致伸缩驱动力向量[P1P2P3Fout]T中，Pj(j=1,2,3)为包含n+1个元素的子向量。其中,永磁体在磁场作用下不产生应变，不受磁致伸缩驱动力作用，所以对应位置的元素为0。在GMM棒上，第j段GMM棒上第i个质-弹-阻单元所受的等效磁致伸缩驱动力可用pji(i=1,2,…，n)表示，如图10所示。

(14)

式中EH——GMM棒弹性模量

S——GMM棒横截面积

fji——第j段GMM棒上第i个质-弹-阻单元所受的磁致伸缩驱动力

可以看出，最后一个永磁体产生的位移即为SGMA的输出位移，经过放大机构放大，最终输出为

xout=Ramp(0,0,…,0,1)X

(15)

5 模型验证

为验证模型的有效性，制作了FASGMA样机，主要参数如表2所示，搭建了以高速数据采集卡(Data acquisition card, DAQ)为核心的实验测试系统。

表2 FASGMA主要参数Tab.2 Main parameters of FASGMA

5.1 实验系统设计

实验测试系统如图11所示，根据功能，该系统大致可以分为4个模块：电源模块、采集模块、致动器模块和主控计算机。

图11 FASGMA实验系统图Fig.11 Photo of experimental system for FASGMA

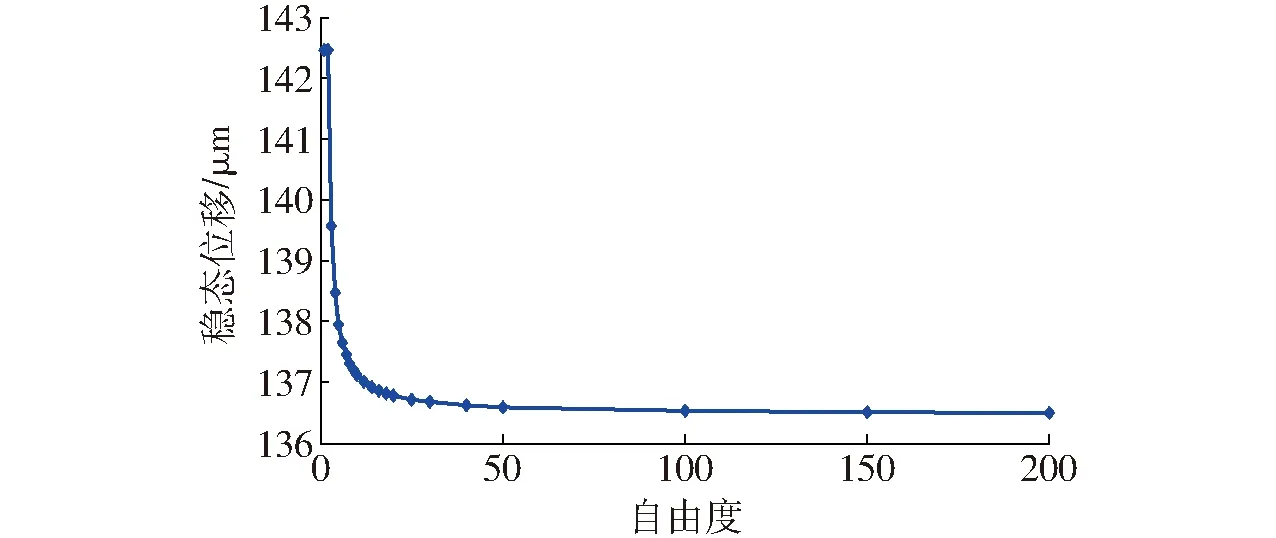
图12 不同自由度对模型计算结果的影响Fig.12 Influence of different DOFs on model calculation result

5.2 模型自由度确定

在位移模型中，SGMA被等效为多自由度振动系统，这样的等效能够有效描述磁场不均匀性对致动器输出的影响。自由度数越多，模型越精细，越接近实际情况。但是，自由度数增加伴随而来的是模型运算量的加大，图12为输入5 A的阶跃电流时，不同自由度下稳态位移的计算结果。

可以看出，单自由度模型与多自由度模型的稳态位移计算值相差约6 μm，当自由度超过50时，模型的计算结果变化不大，所以在实际计算中，自由度数可以选为50。

5.3 实验结果与分析

5.3.1阶跃激励实验

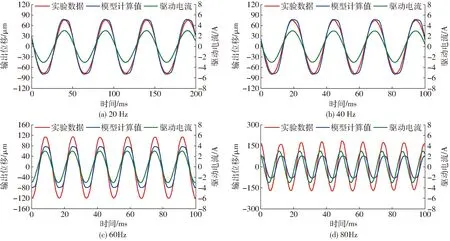
图15 不同频率正弦激励下FASGMA响应曲线Fig.15 Response curves of FASGMA in sinusoidal excitation

图13为输入5A的阶跃电流时FASGMA的响应曲线，可以看出，系统的输出位移约为130 μm，达到稳态的时间约为70 ms。与不连接放大机构的致动器相比，系统的响应时间更长，主要是因为放大机构的等效质量较大，增加了系统的惯性。

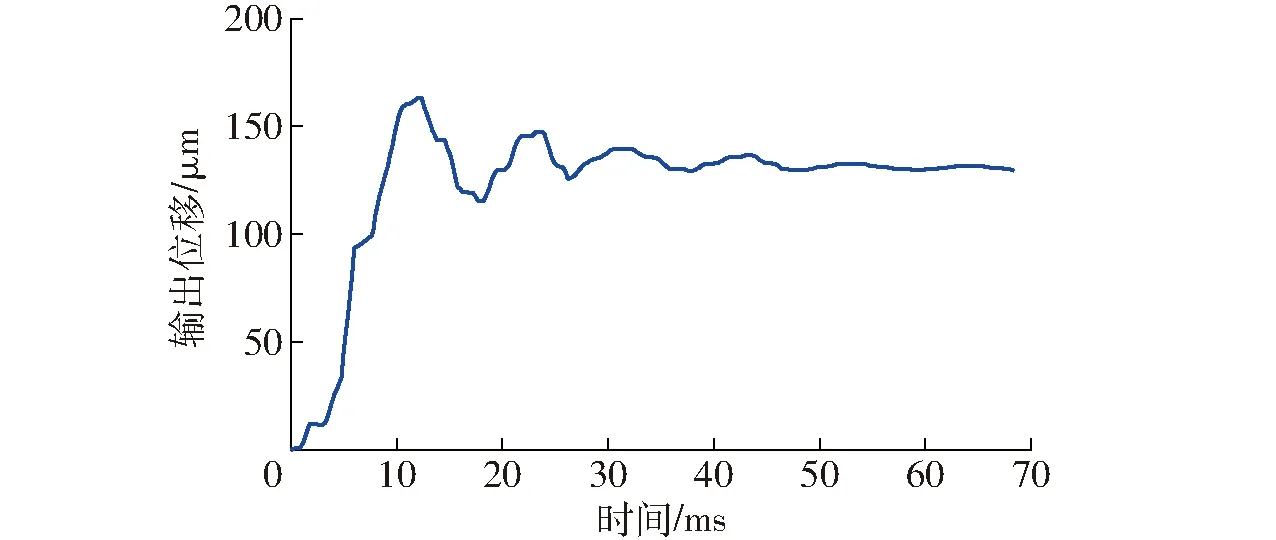
图13 FASGMA阶跃响应曲线Fig.13 Step response curve of FASGMA

在此基础上，将不同幅值的直流电流信号通入致动器，可以得到不同电流下系统的输出位移，与模型计算结果之间的对比如图14所示。

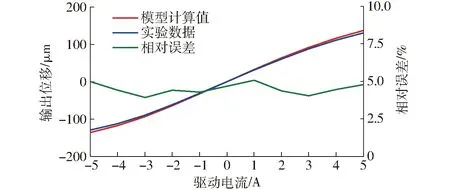
图14 阶跃响应下稳态位移实验与模型对比Fig.14 Comparison of experiment and model results in step response

从图14中可以看出，模型与实验数据之间有较高的吻合度，相对误差基本都在5%以下。最大误差出现在驱动电流为-5 A时，误差约为6.5 μm，相对误差约为5%，说明模型在描绘系统静态特性时有较高的精度。

5.3.2正弦激励实验

在FASGMA中分别施加20、40、60、80 Hz的驱动电流，得到的输出位移曲线与模型计算值如图15所示。可以看出，在实验频率范围内，系统输出与输入之间有较好的跟随特性。当激励频率为20、40 Hz时，模型结果与实验数据吻合度较高。而在60、80 Hz的激励下，实验测得的输出位移明显大于模型计算值，这主要是由于放大机构的一阶固有频率处于60、80 Hz之间，发生了谐振，而且一阶振型与放大机构的主要变形方式在同一平面内，有助于增大系统输出位移。但是需要说明的是，放大机构的一阶振型与目标输出方向不完全相同，这将导致放大机构在一阶共振点附近工作稳定性降低。由图15可看出，当驱动电流频率为80 Hz时，系统各周期的输出位移并不一致，说明系统不宜工作于该频率下。

6 结论

(1)设计了柔性铰链放大的叠堆式超磁致伸缩致动器(FASGMA)，可应用于新型电液伺服阀的驱动。GMM棒和永磁体交替排布的结构形式既保留了两端对置式GMA质量、体积小的优点，同时提高了偏磁场分布的均匀性。柔性铰链放大机构可以有效放大SGMA的输出位移，使最终输出位移满足负载要求。

(2)根据SGMA的结构特点，利用磁路模型和毕奥-萨伐尔定律建立了SGMA磁场模型，结合J-A模型和二次畴转模型建立了SGMA应变模型，模型能够刻画致动器轴线上应变分布的不均匀性。

(3)应用力学基本原理，计算了柔性铰链机构的放大倍数和固有频率，提出了放大机构优化设计方法，确定了机构各结构参数，用有限元方法对计算结果进行了验证。

(4)基于SGMA轴向应变分布不均的特点，考虑SGMA和柔性铰链的相互作用，建立了FASGMA的多自由度位移模型，并根据阶跃响应稳态位移的计算精度确定了自由度的合理取值。

(5)搭建了实验测试系统，完成了FASGMA的阶跃和正弦激励实验。实验表明，阶跃激励下，FASGMA的最大输出位移约为130 μm，与模型误差约为5%，响应时间约为70 ms；正弦激励下，FASGMA能稳定工作于60 Hz以下，对激励信号有较好的跟随特性，输出波形和幅值与模型吻合较好，证明了模型的正确性。

1 贾振元，郭东明. 超磁致伸缩微位移执行器原理与应用[M].北京：科学出版社，2008.

2 张雷, 邬义杰, 王彬, 等. 超磁致伸缩构件精密加工异型孔滑膜控制[J]. 浙江大学学报：工学版, 2012, 46(8): 1412-1418.

ZHANG Lei, WU Yijie, WANG Bin,et al. Non-cylinder holes precision machining by giant magnetostrictive components with sliding mode control[J]. Journal of Zhejiang University: Engineering Science, 2012, 46(8): 1412-1418. (in Chinese)

3 薛光明, 张培林, 何忠波, 等. 强偏置超磁致伸缩致动器准静态位移建模与实验[J/OL]. 农业机械学报, 2015, 46(7): 318-324. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150745&flag=1.DOI:10.6041/j.issn.1000-1298.2015.07.045.

XUE Guangming, ZHANG Peilin, HE Zhongbo, et al. Modeling and experiment of strong bias giant magnetostrictive actuator’ s semi-static displacement[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 318-324. (in Chinese)

4 张雷, 邬义杰, 刘孝亮, 等. 嵌入式超磁致伸缩构建多场耦合优化[J/OL]. 农业机械学报, 2012, 43(5): 190-196.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20120533&flag=1.DOI:10.6041/j.issn.1000-1298.2012.05.033.

ZHANG Lei, WU Yijie, LIU Xiaoliang,et al. Multi-field coupling model of embedded giant magnetostrictive components optimization[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(5): 190-196. (in Chinese)

5 孟爱华, 刘成龙, 陈文艺, 等. 超磁致伸缩致动器的小脑神经网络前馈逆补偿-模糊PID控制[J]. 光学精密工程, 2015, 23(3): 753-759.

MENG Aihua, LIU Chenglong, CHEN Wenyi, et al. CMAC feed forward inverse compensation-fuzzy PID control for giant magnetostrictive actuator[J]. Optics and Precision Engineering, 2015, 23(3): 753-759. (in Chinese)

6 YANG Z, HE Z, LI D, et al. Direct drive servo valve based on magnetostrictive actuator: multi-coupled modeling and its compound control strategy[J]. Sensors and Actuators: Physical, 2015, 235: 119-130.

7 朱玉川, 李跃松. 射流伺服阀用放大型超磁致伸缩执行器建模及分析[J]. 航空学报, 2014, 35(11): 3156-3165.

ZHU Yuchuan, LI Yuesong. Modeling and analysis for amplified giant magnetostrictive actuator applied to jet-pipe electro-hydraulic servovalve[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 3156-3165. (in Chinese)

8 胡均平, 李科军. 磁流体对双喷嘴挡板伺服阀工作性能的影响[J]. 中南大学学报：自然科学版, 2016, 47(7): 2287-2295.

HU Junping, LI Kejun.Influence of magnetic fluids on working performance of twin flapper-nozzle servo valve[J]. Journal of Central South University: Science and Technology, 2016, 47(7): 2287-2295. (in Chinese)

9 SMITH R. A nonlinear physics-based optimal control method for magnetostrictive actuators[J]. Journal of Intelligent Material System and Structure, 1998, 9(6): 468-486.

10 STACHOWIAK D. The influence of magnetic bias and prestress on magnetostriction characteristics of a giant magnetostrictive actuator[J]. Przeglad Elektrotechniczny, 2013, 89(4): 233-236.

11 杨旭磊, 朱玉川, 费尚书, 等. 超磁致伸缩电静液作动器磁场分析与优化[J]. 航空动力学报, 2016, 31(9): 2210-2217.

YANG Xulei, ZHU Yuchuan, FEI Shangshu, et al. Magnetic field analysis and optimization of giant magnetostrictive electro-hydrostatic actuator [J]. Journal of Aerospace Power, 2016, 31(9): 2210-2217. (in Chinese)

12 BRAGHIN F, CINQUEMANI S, RESTA F. A low frequency magnetostrictive inertial actuator for vibration control[J]. Sensors and Actuators A: Physical, 2012, 180: 67-74.

13 ZHANG H, ZHANG T, JIANG C. Design of a uniform bias magnetic field for giant magnetostrictive actuators applying triple-ring magnets[J]. Smart Materials and Structures, 2013, 22: 115009.

14 HALL D L. Dynamics and vibrations of magnetostrictive transducers [D]. Iowa City: Iowa State University, 1994.

15 WANG X, WU J, JIA Z, et al. Mechanical and magnetic analysis of giant magnetostrictive transducer[J]. Applied Mechanics and Materials, 2011, 79: 166-171.

16 牟星, 唐海军, 高学绪, 等. 超磁致伸缩致动器中偏置磁场的有限元模拟[J]. 磁性材料及器件, 2014, 45(4): 6-10.

MOU Xing, TANG Haijun, GAO Xuexu, et al. Finite element modeling of magnetic bias field for magnetostrictive actuator[J]. Journal of Magnetic Materials and Devices, 2014,45(4):6-10. (in Chinese)

17 YANG Z, HE Z, LI D, et al. Bias magnetic field of stack giant magnetostrictive actuator: design, analysis and optimization[J]. Advances in Materials Science and Engineering, 2016, 2016: 1-13.

18 董云峰, 曲兴田, 沈传亮, 等. 压电直接驱动式伺服阀[J]. 吉林大学学报：工学版, 2006, 36(5): 678-680.

DONG Yunfeng, QU Xingtian, SHEN Chuanliang,et al. Servo-valve driven by piezoelectric ceramics[J]. Journal of Jinlin University: Engineering and Technology Edition, 2006, 36(5): 678-680. (in Chinese)

19 QI K, YANG X, CHAO F, et al. Analysis of the displacement amplification ratio of bridge-type[J]. Mechanism and Machine Theory, 2015, 87: 45-56.

20 凌明祥, 刘谦, 曹军义, 等. 压电位移放大机构的力学解析模型及有限元分析[J]. 光学精密工程, 2016, 24(4): 812-818.

LING Mingxiang, LIU Qian, CAO Junyi, et al. Analytical model and finite element piezoelectric displacement amplification mechanism[J]. Optics and Precision Engineering, 2016, 24(4): 812-818. (in Chinese)