基于流声耦合法的超低比转数离心泵空化特性研究

王 勇 赵宇琪 董 亮 代 翠 刘厚林 徐海良

(1.江苏大学流体机械工程技术研究中心， 镇江 212013; 2.江苏大学能源与动力工程学院， 镇江 212013;3.君禾泵业股份有限公司， 宁波 315171)

引言

离心泵被广泛应用于潜艇、舰船和航空航天等各个领域[1-3]。随着泵行业朝高速化、大型化方向发展，空化问题已成为限制其发展的重要因素[4]。空化的产生不仅造成过流部件的破坏，使泵运行可靠性降低，还会因振动噪声影响泵运行稳定性[5]。很多情况下，空化的产生是无法避免的[6]。因此，需要提高空化的监测精度，降低由空化带来的不必要损失。

传统工业上的空化监测法有涂层侵蚀法[7]及压降判断法[8]。当空化空泡溃灭时产生的激波脉冲振幅大于附着材料的许用应力极限时，材料表面将形成微坑[9]。根据这一特性，在过流部件上喷涂检测油漆成为空化判断的原始方法，其难点在于选择粘合性和敏感性适当的喷漆。由于空化影响水力性能，因此常以扬程降低3%作为空化判断标准[10]。此外，根据效率、流量、转矩和临界空化系数之间的关系判断空化也是较为常用的检测手段[11-14]。然而，这些方法只能判断发展到一定阶段的空化，无法进行实时监测[15-16]。空化的产生会诱导低频的压力振荡和高频的压力脉冲，它们都会以噪声的形式表现出来[17-18]。且随空化数的降低，泵内会依次出现空泡空化[18]、片状叶面空化[19]、超空化[20]等不同形式的空化状态，因此不同空化阶段，声场分布也存在差异[21]。研究不同空化阶段噪声信号变化规律，可以为空化声学诊断提供依据。

CUDINA等[22-23]通过试验发现，噪声谱中存在一个离散频率特征值与泵内部空化发展过程相对应，并以此为根据监控空化的初生，该方法比工业中以扬程下降3%作为判断依据更加准确。ZEQIRI等[24]通过布置在水轮机叶片上的水听器监测空化噪声，此方法虽然能够测量到未衰减的空化原始信号，但会受到动静干涉作用的干扰，因此适用性受到极大制约。刘源等[25]将小波熵法引入空化诱导噪声中，提出了基于小波熵的空化初生检测和空化状态识别方法。张俊华等[26]用宽频传感器测试不同空化程度下的声信号，分析声信号的频谱特征随空化发展的变化规律，根据声谱特性对空化阶段进行划分。戚定满等[27]对瞬态的空化噪声信号进行小波变换，研究小波系数随时间和频率的变化图像，以及空化噪声谱随时间的变化规律。卿彪[28]通过对空化噪声信号功率谱的分析，发现空化特征信号主要集中在低频段，由此定义了两个功率阈值区间，以定量地判断离心泵空化发展的程度。

本文应用CFD结合Lighthill声类比理论，研究空化对内流场及内部声场的影响，为通过声信号判断空化程度提供依据。

1 试验测试

1.1 试验装置

试验在江苏大学流体机械工程技术研究中心闭式试验台上进行，试验装置包括汽蚀罐、稳压罐、进出水管路、进出口闸阀、真空泵、电动机、电磁流量计、压力传感器、水听器、泵产品参数测量仪及高性能数据采集系统等。图1为闭式试验台装置示意图。

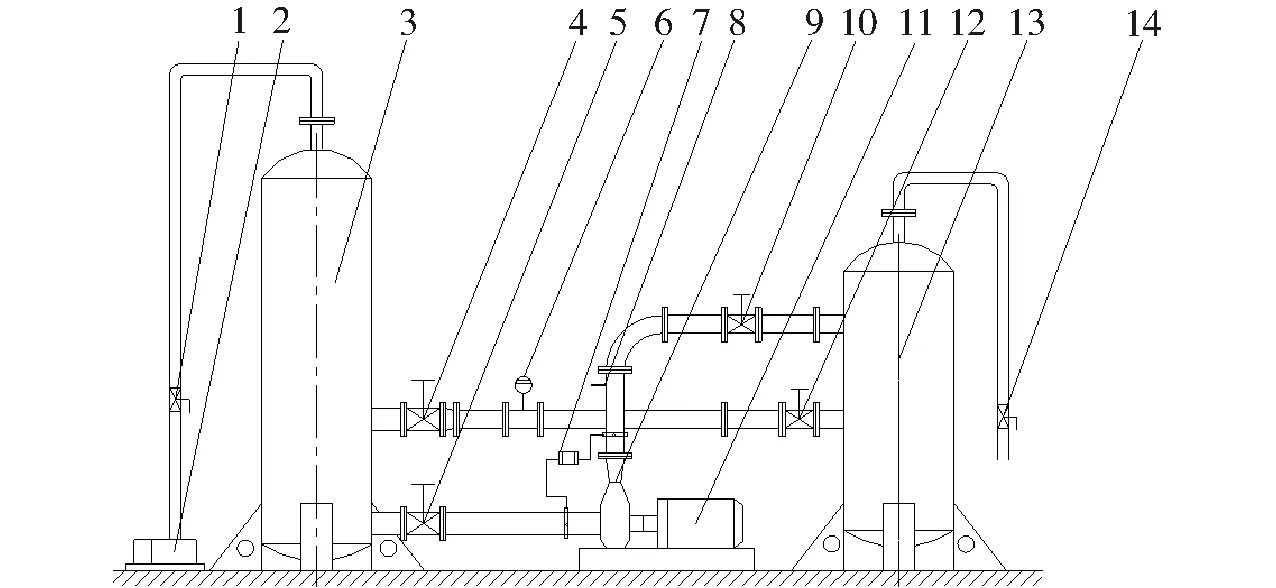
图1 试验台装置示意图Fig.1 Sketch of experiment equipment1、14.球阀 2.真空泵 3.汽蚀罐 4、5、10、12.闸阀 6.电磁流量计 7.压力传感器 8.水听器 9.模型泵 11.电动机 13.稳压罐

采用INV3020C型高性能24位数据采集系统对内场噪声信号进行采集，并进行数据的处理分析。其中内场噪声信号通过RHSA-10型水听器测量，其线性工作范围20～100 kHz，灵敏度-188 dB，满足对空化信号采集的精度要求。水听器的安装方式一般分为3种类型：内置式安装、平齐式安装、管道-容腔式结构。其中内置式安装会因水听器表面的湍流区脉动压力而产生“伪声”，从而形成强烈的背景噪声，产生较大测量误差。管道-容腔式测量系统的固有频率随传压管与容腔体积的增大而减小，而随传压管面积的增大而增大，因此噪声的频率范围受到限制。平齐式安装能够可靠地测量水管中脉动声场，同时对管中流场影响最小；不足之处是测量会受到管壁边界层噪声影响，但文献[29]表明，边界层噪声相比脉动噪声量级很小，可认为水听器监测值即为泵内部空化流动噪声。且由于水听器灵敏度较高，容易受泵出口压力脉动影响，因此需布置在远场端，一般位于距离泵出口法兰6～8倍管径处。因此声场测点位置位于距离泵出口法兰8倍管径处，采用与管道平齐式安装法。流量测量采用KEF-DN50型电磁流量计，工作压力4.0 MPa，量程1～50 m3/h，精度等级0.5级。为保证测量精度，流量计前后直管段长度均为10倍流量计内径。压力测量：采用MIK-P300型压力传感器，进口压力传感器量程为-0.1～0.1 MPa，出口压力传感器量程为0～1 MPa，精度0.5级。进出口测压点位置距离泵进出口法兰2倍管径处。

1.2 试验对象

试验对象为一比转数ns=25的超低比转数离心泵。设计工况主要参数为：流量Qd=12.5 m3/h，扬程Hd=74 m，转速nd=2 950 r/min。叶轮为闭式，泵主要结构参数如表1所示。

表1 离心泵主要结构参数Tab.1 Main geometry parameters

1.3 试验步骤

试验时确保泵进口管路闸阀保持全开，避免阀门影响进口流场及阀门处空化对下游泵空化噪声的测量产生影响。为保证试验准确性，每组试验进行3次。

(1)启动试验用泵，待泵运行稳定后通过调节稳压罐下游阀门开度，使泵在额定工况下运行。

(2)泵流量稳定在12.5 m3/h后，启动真空泵，通过降低汽蚀罐内压力降低空化系数。

(3)真空泵每次启动5 s，以确保试验细节的完整。真空泵关闭后，流量会有微小变化，此时再通过调节稳压罐下游阀门开度，使泵流量稳定在额定流量。

(4)通过高速采集系统对信号量进行同步采集、分析、处理。

为真实反映非定常瞬态信号，需要设置合适的采样频率以保证采集信号对原始信号的真实还原。采样频率过高会发生信号的混叠；采样频率过低则会导致无法捕捉到特征信号，使得采集信号失真。根据奈奎斯特采样定理，取采样频率为分析频率的3～4倍。本文采样频率设置为12.8 kHz，时间30 s。

2 流场及声场计算

2.1 流场模拟方法

流场计算域包括5部分：进口延长段、吸水室、叶轮水体、蜗壳水体、出口延长段。利用ANSYS ICEM对水体进行高质量结构化网格划分。流体域与网格如图2所示。

图2 计算流体域及网格Fig.2 Computational model and grid

网格无关性检查如表2所示。对比5套不同数量的网格扬程预测值，综合考虑，选择方案4网格，网格单元总数为1.79×106。

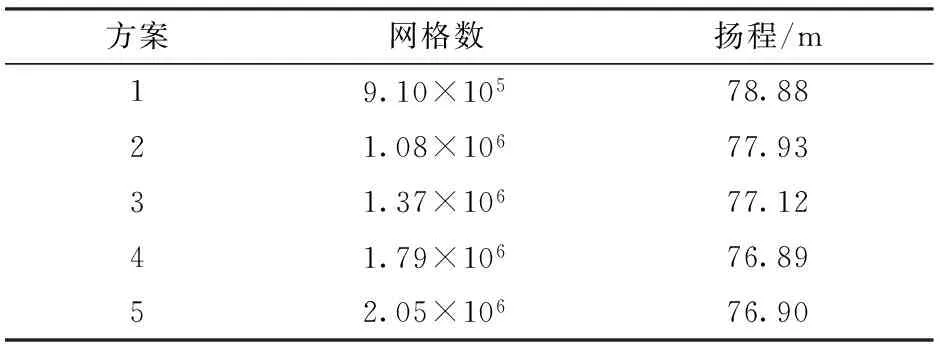
表2 网格无关性验证Tab.2 Inspection of grid independence

利用流体计算软件CFX对低比转数离心泵内部流场进行定常及非定常计算。其中叶轮流场采用旋转坐标系，其余流场设置为静止坐标系。进口边界条件设置为总压101 kPa，出口边界条件设置为质量流量。所有壁面均采用无滑移壁面，粗糙度为20 μm。在动静部件间使用交界面进行数据交换，其中对于定常计算，使用冻结转子交界面，而对非定常计算，采用瞬态动静交界面，网格关联采用GGI方式。定常和非定常计算湍流模型均选用SST湍流模型，它与标准k-ε湍流模型相比在近壁面处具有更好的鲁棒性，同时避免k-ω模型对入口湍动过于敏感的劣势，因此应用广泛且具有较高的可信度。

非定常数值计算中，时间步长设置为ΔT=0.000 056 5 s，即叶轮旋转1°所需时间，当流场呈现出明显周期性且达到稳定后，提取最后8个旋转周期数据作为噪声计算激励源。

2.2 空化计算

在空化数值计算中，除了湍流封闭之外，还需要增加空化模型方程来求解由于控制方程而增加的未知参量。空化流场计算准确性很大程度上依赖空化模型的选择，其中均匀介质平衡流模型常被用于复杂三维旋转机械空化模拟中。分别选取Kunz空化模型[30]及Zwart空化模型[31]对泵空化流场进行模拟，得到空化性能曲线如图3所示。

图3 空化性能曲线Fig.3 Cavitation performance curves at different flow rates

扬程系数和空化系数的计算公式为

(1)

(2)

式中H——扬程，m

u2——叶轮出口圆周速度，m/s

pin——叶轮进口处压力，Pa

pv——介质饱和蒸气压，Pa

ρl——介质密度，kg/m3

从图3中可以看出，对于低比转数离心泵，Kunz模型及Zwart模型在未空化阶段预测扬程系数均高于试验值，空化模型对未发生空化时泵扬程系数的数值预测几乎没有影响。Kunz模型预测得到的空化性能曲线比Zwart下降快，因为Zwart模型是基于气液两相连续方程推导得出的净相变率表达式，然后在空泡的生成和溃灭过程相同的基础上对净相变率做了一定修正，而Kunz模型考虑了与雷诺数相关的特征长度与自由流速度，因此二者对超低比转数离心泵预测有所差异。为比较不同空化模型的预测精度，各空化系数下预测值和试验值如表3所示。

表3 不同空化模型预测结果与偏差Tab.3 Prediction results and deviations of differentcavitation models

可以看出，Zwart模型在临界空化状态对性能的模拟更加接近试验值。Zwart空化模型是基于Rayleigh-Plesset(R-P)方程推导得出，若考虑表面张力和粘性效应，则R-P方程表达式为

(3)

式中RB——空泡半径

μl——液体的湍流动力粘度

T——表面张力系数

pv——饱和气化压力

t——变化时间p——设置压力

假设空泡间是相互独立的，忽略二次项、湍流粘度项与表面张力项，则R-P方程可简化为

(4)

假设空泡为球形，mB表示单空泡的质量，可得出单空泡单位时间内的质量交换率为

(5)

若液体单位体积内有NB个空泡，单位时间内单位体积的气液两相质量交换率为

(6)

式中ρv——汽相密度

采用rnuc(1-αv)代替液体气化过程中的空泡体积分数αv，最终形式的Zwart空化模型为

(7)

(8)

式中Re——气化项Rc——凝结项

rnuc——成核位置体积分数

Fvap——气化过程经验校正系数

Fcond——凝结过程经验校正系数

在CFX中，以上经验系数的默认值分别为rnuc=5×10-4,RB=1.0×10-6m，Fvap=50，Fcond=0.01，pv=3 574 Pa。

2.3 声场计算

确定合适的空化模型后，进行非定常声源信息计算提取。在流动声学问题中，流场和声场是统一的[32]。目前，应用最广的解决流场中运动物体发声问题的FW-H方程为

(9)

式中Tij——Lighthill应力张量

δij——Kronecher函数

ρ——流体密度

ρ0——未受扰动时流体密度

ui——流体速度

p′——流体受到的压强变化量

c0——声速

f——控制边界函数

xi、xj——方向分量

考虑主要声源并对等式两边进行Fourier变换，得到频域的Helmholtz方程，利用自由空间的Green函数，可以得到辐射声压

(10)

式中r0、rs——场点和源点的位置矢量

p(rs)——边界上的流体压力

S——流体边界所围面积

n——边界垂直方向分量

k——滤波函数

整个计算均在LMS Virtual.Lab平台实现，采用DBEM(直接边界元法)对声场进行求解，其声源信息直接在非定常流体计算结果中提取。噪声计算过程中利用快速傅里叶变换将时域脉动转换为频域脉动，并映射至声学网格。以加速度作为边界条件，进出口定义为全吸声属性，其余表面假设为全反射壁面，特性声阻抗Z=ρc0=1.5×106kg/(m2·s)，其中声速为1 500 m/s。场点设置在距离泵出口法兰8倍管径处(与试验测点相同)，并进行声压级换算。

3 结果与分析

3.1 内流场计算结果

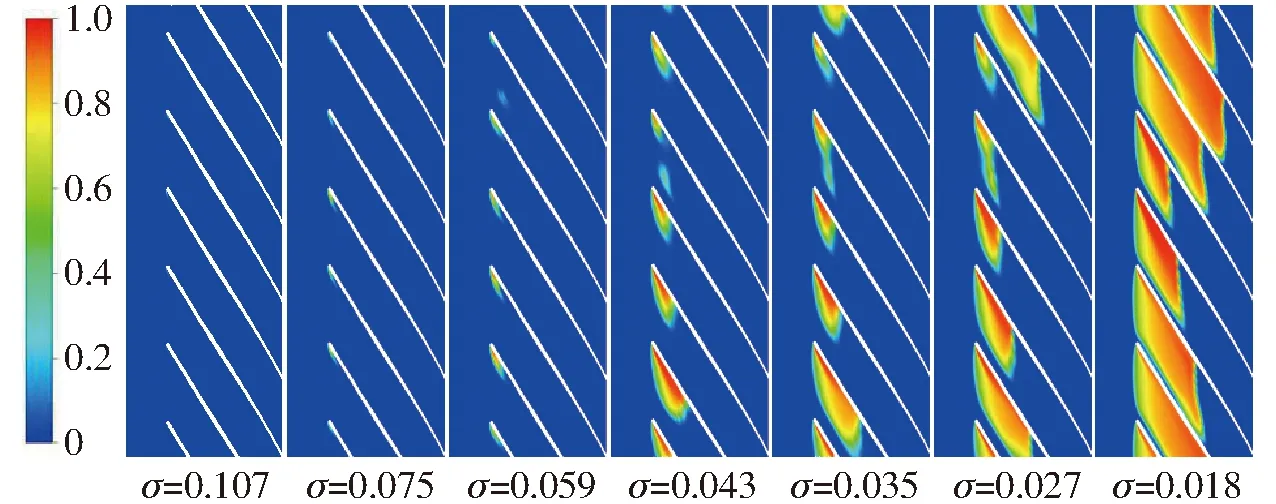
图4 不同空化系数切面上叶片间空泡体积分数分布Fig.4 Vapor volume fraction distribution among blades section with different σ

图4为额定工况下不同空化系数条件下span为0.5切面上的叶片间气相体积分数分布。其中，span定义为从叶轮后盖板到前盖板之间的无量纲距离，取值范围为0～1。通过span值调整展开平面位置，span为0.5时表示该面位于距离前后盖板位置相等处。

从图4中可以看出，空泡最先出现在叶片进口吸力面；随着空化系数的减小，空化程度逐渐加剧，空泡分布沿叶片距离增加；空泡分布的不对称，可能是由于蜗壳、吸水室的不对称性造成的。根据空泡分布情况及空化性能曲线，将整个空化过程定义为4个阶段。

(1)未空化阶段(σ> 0.107)：整个过程无空泡产生，空化性能曲线均呈水平状态。叶轮切平面无气相分布。

图5 不同空化系数下内流及空泡分布Fig.5 Vapor volume fraction distributions of internal flow with different cavitation stages

(2)空化初生阶段(0.107 >σ> 0.043)：开始有少量空泡出现在叶片进口吸力面，此空化阶段水力性能未受影响，空化性能曲线点仍保持水平状态。

(3)特征空化阶段(0.043>σ>0.018)：空泡量增大，泵水力性能受到影响，扬程下降3%～5%；空泡沿叶片吸力面长度占叶片吸力面边长的1/3～1/2。

(4)严重空化阶段(σ< 0.018)：叶轮的流道被气泡大量占据，液泡痕迹延伸到叶片入口的压力侧，空泡沿叶片吸力面长度占叶片吸力面边长的1/2以上。此时内部流动被严重影响，扬程急剧下降。

由于泵叶轮为6叶片，因此叶轮每转过60°为一个周期。图5(图中t0表示初始时间)给出了额定工况下4个不同空化阶段内部流线及压力分布在1个周期内变化情况。

从图5可以看出，随着空化系数的降低，内部流动发生明显变化。从图5a、5b中可以看出漩涡尺度在即将通过隔舌位置所对叶轮流道内发展至最大，当此流道通过隔舌后，涡尺度明显减小。这是由于流道通过隔舌位置时，大尺度的涡被分散，一部分携带能量进入蜗壳出口，引起压力波动并产生振动噪声，另一部分继续在流道内发展，并随叶轮旋转。当再次转到即将通过隔舌位置时，涡尺度发展至最大。此外，在未空化阶段及空化初生阶段，流线及压力分布变化不明显，因此可以说明，少量游移及附着空泡的产生不足以破坏整个流动的稳定性，空化对流场影响可以被忽略。从图5c可以看出，特征空化阶段叶轮及蜗壳内压力波动明显变大，且叶轮流道内涡数量增加。与未空化阶段及空化初生阶段相比，远离隔舌位置对应叶轮流道内流态最差。这是由于隔舌位置所对流道内压力较高，而远离隔舌位置流道内压力较低，空化在压力较低处更加严重，导致流态变差。从图5d可以看出，在严重空化阶段，除隔舌对应叶轮流道内流态较好，其他流道涡数量继续增加，流态变差。空泡体积分数分布从隔舌位置到远离隔舌位置逐渐增加，压力分布在接近隔舌位置增加。说明空化的产生对流态影响较为明显。而内部流态的变化会对声场产生影响，使噪声信号发生变化。

3.2 内声场计算结果

由于流体流经离心泵时，在旋转叶轮的影响下使得流动变得复杂，而噪声更易随液流向下游传播，因此声场计算时监测点设置在距离泵出口8倍管径处。图6为4个不同空化阶段模拟值及试验值在0～3 000 Hz的声压级频谱，其中，对试验信号进行快速傅里叶变换处理，为减小因在时域截断信号而在频域中产生泄漏误差，数据处理时均加Hanning窗得到频谱曲线。内场噪声声压级公式为

(11)

式中pa——声压的有效值，Pa

p0——基准声压，水中基准声压取10-6Pa

图6 各空化阶段频谱分布试验值与模拟值对比Fig.6 Comparison of experimental and simulated values of sound pressure level spectrum of internal noise at various cavitation stages

可以看出，离心泵噪声在整个频域范围均呈现宽频特征，但在轴频(49 Hz)、叶频(295 Hz)及其倍频处峰值较高。其中叶频峰值较大,说明旋转叶片与固定隔舌处的动静干涉作用是离心泵诱导噪声的主要原因，而试验值中与轴频及轴频倍频分量等相关离散信号及轴频附近宽频信号应该是由于安装精度或加工精度所造成的机械噪声，因此在模拟值中未有体现。

由于动静干涉作用产生的噪声为离散噪声，因此在未空化阶段，能量主要集中于低频区轴频、叶频及其倍频处，且特征值分量多集中于2 000 Hz以下频段。当频率大于2 000 Hz，离散特征明显减弱，特征信号被淹没在宽频带内。因此，动静干涉作用主要集中于小于2 000 Hz的中低频段。进入空化初生阶段，从内场分析可知，此时空化空泡数量不足以影响内部流动，因此低频区叶频及其倍频分量变化不明显。但由于空泡游移及空泡溃灭所引起的高频脉动，使2 000 Hz以上频带诱导噪声信号上升。进入特征空化阶段，气泡已对内流场造成严重影响，流道内流体逐渐变成两相流造成脉动量级减小；同时，由于气泡堵塞部分流道，影响叶片及隔舌处的动静干涉作用向上游传播，使得叶频不再是主频。由图6c可知，叶频及其倍频分量减小，轴频分量得以突出，宽频带声压级整体上升，且在高频段上升明显，一方面说明声压信号在整个频谱均有能量存在，空化诱导噪声为宽频噪声；另一方面也反映出空化诱导噪声能量多集中于高频段。严重空化阶段，宽频带声压级继续升高，特征值分量降低，且特征值旁瓣声压级增加。而此时流道内空泡已严重阻碍液流流动，空泡大面积产生及溃灭时所产生的噪声及空泡游移溃灭诱导壁面振动所产生的噪声，在流场计算时无法获取。因此模拟值与试验值存在一定差距。

由于旋转机械噪声具有明显的特征值，表4(表中fa表示轴频；fb表示叶频)给出了几个特征频率下不同空化阶段预测值与试验值相对误差以及总声压级预测误差。而由于空化噪声的宽频特性，将不同空化阶段下噪声1/3倍频程谱模拟值和试验值进行对比，以分析其相对误差。总声压级Lp计算公式为

(12)

式中 Δfi——计算时最小分辨率

f0、fmax——计算频率极限

表4 不同空化阶段噪声特征值相对误差及总声压级相对误差Tab.4 Absolute error of noise characteristic valueand total sound pressure level at differentcavitation stages %

从表4分析可知，轴频处模拟值与试验值差距较大，叶频及叶频倍频在不同空化阶段的预测值与试验值相差较小。预测值整体上比试验值高。未空化阶段及空化初生阶段，特征频率声压级是影响总声压级的主要因素，特征值误差基本小于5%。

图7为不同空化阶段模拟值相对误差分布，从图7可以看出偏差较大处主要集中于50 Hz以下和1 000 Hz附近频带处，此频带能量较低，因此误差对总声压级的贡献量较小。特征空化及严重空化阶段，特征值不再是影响总声压级的主要因素，因为空化噪声主要体现为宽频特性，宽频声压级贡献量大幅提高。因此，虽然在特征频率处声压级相对误差有下降趋势，但从图7可以看出，在100～1 000 Hz能量较高频带内，声压级误差相对较大，造成总声压级预测误差的增大。

图7 各空化阶段模拟值相对误差分布Fig.7 Absolute error distribution of simulated values for each cavitation stages

预测偏差存在于多个方面，一方面在于选择的湍流模型或空化模型在流场计算时的一些假设与简化，使得数值模拟难以完全与实际流动对应；此外，在声场计算求解FW-H方程时，由于仅考虑主要声源，对单极子和四极子声源的简化使得计算存在一定偏差。由于流声耦合计算涉及计算流体力学与气动噪声学，模型相互调用时的一些简化与假设，理论上也会对计算结果产生一定影响。

从图7还可以看出，预测值与试验值在各空化阶段各频段相对误差基本小于10%，尤其在空化初生阶段的中频带，预测误差基本小于5%，预测精度较高，可以为依据声信号进行空化监测提供参考。为定量分析流声耦合法对空化噪声变化规律的预测准确性，在空化初生阶段附近选取更多工况进行模拟，得到叶频及其倍频处声压级、总声压级、高频倍频程声压级变化趋势与空化系数的关系曲线，如图8所示。

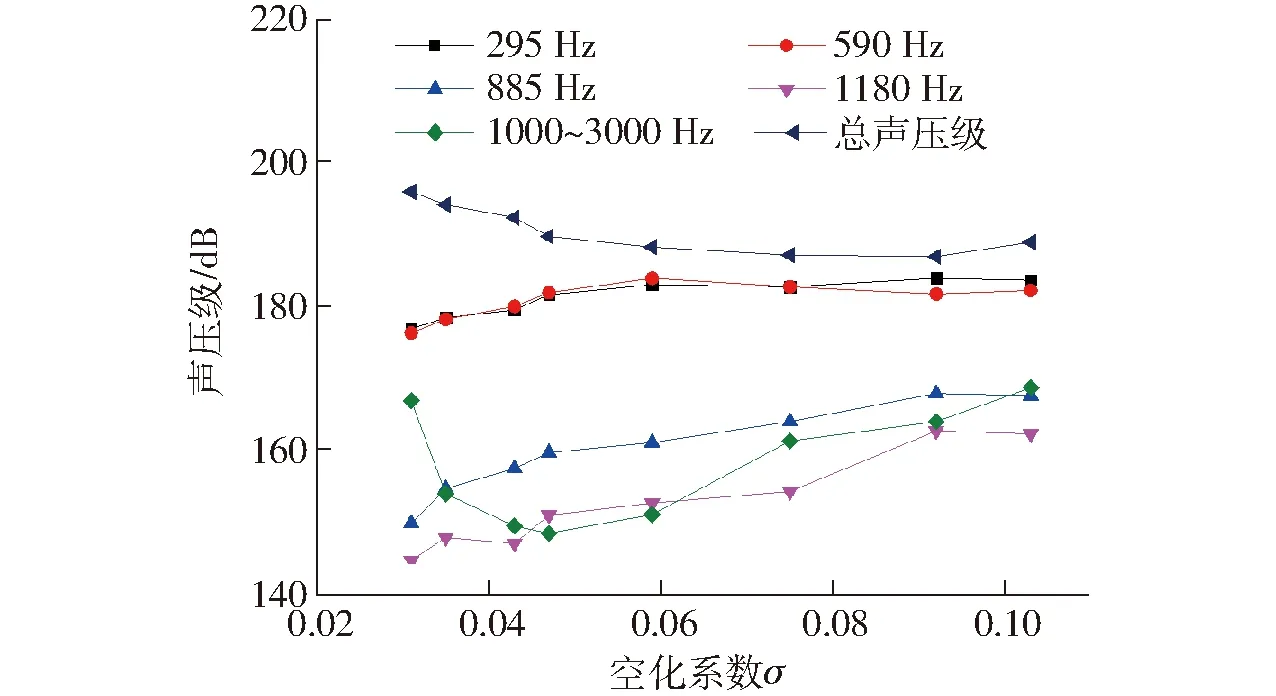
图8 特征频率声压级随空化系数变化趋势Fig.8 Changing trends of sound pressure level of characteristic frequencies at different cavitation coefficients

从图8可以看出，总声压级在空化初生阶段呈现先缓慢减小、再逐渐增加的规律。其他不同特征频率监测量随空化系数变化的规律不同。随空化系数减小，叶频及其倍频分量呈现缓慢降低的变化趋势，当即将达到特征空化时，降低趋势更加明显。而1 000～3 000 Hz频带，随空化系数的减小，呈现减小趋势，当进入空化初生阶段声压级开始上升，特征空化阶段上升明显。这与实际声压级变化情况相符，由此也可以看出，基于流声耦合法计算空化噪声是可行的，且能够预测空化噪声总体变化规律。

4 结论

(1)Zwart模型相比Kunz模型对超低比转数离心泵空化模拟具有更好的适用性，预测值更加接近试验值。

(2)基于流声耦合算法可以模拟离心泵不同空化阶段内场噪声，与试验结果相比，在未空化阶段及空化初生阶段具有很好的吻合度，相对误差基本小于5%。在特征空化阶段及严重空化阶段，吻合度稍差，相对误差基本小于10%。

(3)空化的发展对动静干涉具有一定抑制作用，使得叶频及其倍频特征值离散分量声压级随空化的发展呈现逐渐下降趋势，而轴频分量呈现增大趋势。

(4)空化噪声能量主要集中于1 000 Hz以上的高频段；高频宽频噪声随空化系数的降低呈现先缓慢减小、然后急剧上升的规律，逐渐将高频特征值分量淹没在宽频带中。

1 付建, 宋振海, 王永生,等. 泵喷推进器水动力噪声的数值预报[J]. 船舶力学, 2016, 20(5):613-619.

FU Jian, SONG Zhenhai, WANG Yongsheng, et al. Numerical predicting of hydroacoustics of pumpjet propulsor[J].Journal of Ship Mechanics, 2016, 20(5):613-619. (in Chinese)

2 张瑶, 罗先武. 离心泵叶轮进口前非定常流动研究[J]. 舰船科学技术, 2015(1):39-44.

ZHANG Yao, LUO Xianwu. Investigation on the unsteady flow field upstream of a centrifugal pump impeller[J]. Ship Science and Technology, 2015(1):39-44. (in Chinese)

3 王珺, 胡鹏, 颜勇. 液体火箭发动机泵的POGO气蚀动特性试验研究[J]. 火箭推进, 2012, 38(4):26-31.

WANG Jun, HU Peng, YAN Yong. Experimental investigation of POGO cavitation dynamic characteristic for liquid rocket engine pump[J]. Journal of Rocket Propulsion, 2012, 38(4):26-31. (in Chinese)

4 王维军, 王洋, 刘瑞华,等. 离心泵空化流动数值计算[J/OL]. 农业机械学报, 2014, 45(3):37-44.http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20140307&flag=1&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2014.03.007.

WANG Weijun, WANG Yang, LIU Ruihua, et al. Numerical calculation of cavitation flow in a centrifugal pump[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(3):37-44. (in Chinese)

5 王勇, 刘厚林, 袁寿其,等. 离心泵非设计工况空化振动噪声的试验测试[J]. 农业工程学报, 2012, 28(2):35-38.

WANG Yong, LIU Houlin, YUAN Shouqi, et al. Experimental testing on cavitation vibration and noise of centrifugal pumps under off-design conditions[J]. Transactions of the CSAE, 2012, 28(2):35-38. (in Chinese)

6 潘中永, 袁寿其. 泵空化基础[M]. 镇江：江苏大学出版社, 2013:4-8.

7 黄旭, 张敏弟, 付细能. 涂层对空化流动特性影响的试验研究[J]. 船舶力学, 2015(1-2):35-42.

HUANG Xu, ZHANG Mindi, FU Xineng.Experimental study of coatings’effect on cavitating flow[J]. Journal of Ship Mechanics, 2015(1-2):35-42. (in Chinese)

8 李军, 刘立军, 李国君,等. 空化数对离心泵水力性能影响的数值研究[J]. 工程热物理学报, 2007, 31(5):773-776.

LI Jun, LIU Lijun, LI Guojun, et al. Numerical investigations on effects of cavitation number on hydrodynamic performance of centrifugal pump[J]. Journal of Engineering Thermophysics, 2007, 31(5):773-776. (in Chinese)

9 李栋梁, 邹冠驰, 郑根土,等. 微观组织对空化作用下不锈钢表层力学性质的影响[J]. 材料研究学报, 2012, 26(3):274-278.

LI Dongliang, ZOU Guanchi, ZHENG Gentu, et al. Effects of the microstructures on surface layer mechanical properties of stainless steels under cavitation[J]. Chinese Journal of Materials Research, 2012, 26(3):274-278. (in Chinese)

10 李晓俊, 袁寿其, 潘中永,等. 诱导轮离心泵空化条件下扬程下降分析[J]. 农业机械学报, 2011, 42(9):89-93.

LI Xiaojun, YUAN Shouqi, PAN Zhongyong, et al. Analysis of cavitation head drop in centrifugal pump with inducer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(9):89-93. (in Chinese)

11 李晓俊, 袁寿其, 刘威,等. 带诱导轮的离心泵空化条件下的效率下降规律[J]. 排灌机械工程学报, 2011, 29(3):185-189.

LI Xiaojun, YUAN Shouqi, LIU Wei, et al. Efficiency degrade law under cavitation conditions of centrifugal pump with inducer[J].Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(3):185-189. (in Chinese)

12 卢加兴, 袁寿其, 任旭东,等. 离心泵小流量工况不稳定空化特性研究[J/OL]. 农业机械学报, 2015, 46(8): 54-58. http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20150809&flag=1&journal_id =jcsam. DOI: 10.6041/j.issn.1000-1298.2015.08.009.

LU Jiaxing, YUAN Shouqi, REN Xudong, et al. Investigation of instabilities of cavitation at low flow rate of centrifugal pump[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2015, 46(8):54-58. (in Chinese)

13 段向阳, 王永生, 苏永生,等. 离心泵空化监测试验[J]. 振动、测试与诊断, 2011, 31(3):385-388.

DUAN Xiangyang, WANG Yongsheng, SU Yongsheng, et al. Experimental study of cavitation monitoring in centrifugal pump[J]. Journal of Vibration Measurement and Diagnosis, 2011, 31(3):385-388. (in Chinese)

14 郝宗睿, 刘锦涛, 王乐勤. 水泵水轮机临界空化系数的数值预测[J]. 排灌机械工程学报, 2013, 31(9):774-777.

HAO Zongrui, LIU Jintao, WANG Leqin. Numerical prediction of critical cavitation number in pump-turbine[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(9):774-777. (in Chinese)

15 段向阳, 王永生, 苏永生. 水力机械空化(汽蚀)监测研究综述[J]. 水泵技术, 2008(5):1-6.

DUAN Xiangyang, WANG Yongsheng, SU Yongsheng. Study on cavitation monitoring of hydraulic machinery[J]. Pump Technology, 2008(5):1-6. (in Chinese)

16 段向阳, 王永生, 苏永生. 振动分析在离心泵空化监测中的应用[J]. 振动与冲击, 2011, 30(4):161-165.

DUAN Xiangyang, WANG Yongsheng, SU Yongsheng. Vibration analysis applied in cavitation monitoring of a centrifugal pump [J]. Journal of Vibration and Shock, 2011, 30(4):161-165. (in Chinese)

17 宋启策, 赵伟国, 杨军虎,等. 泵空化现象的研究综述[J]. 机械制造, 2014, 52(9):1-5.

SONG Qice, ZHAO Weiguo, YANG Junhu, et al. A review of pump cavitation[J]. Machinery Manufacturing, 2014, 52(9):1-5. (in Chinese)

18 张磊, 文青, 赵子梦,等. 基于多模式超声场作用下的空泡空化机理[J]. 江苏大学学报：自然科学版, 2017, 38(3):302-307.

ZHANG Lei, WEN Qing, ZHAO Zimeng, et al. Cavitation mechanism of bubbles under multi-mode ultrasonic field[J]. Journal of Jiangsu University :Natural Science Edition, 2017, 38(3):302-307. (in Chinese)

19 杨琼方, 王永生, 张志宏. 螺旋桨空化初生的判定和空化斗的数值分析[J]. 上海交通大学学报, 2012, 46(3):410-416.

YANG Qiongfang, WANG Yongsheng, ZHANG Zhihong. Determination of propeller cavitation initial inception and numerical analysis of the inception bucket[J]. Journal of Shanghai Jiaotong University, 2012, 46(3):410-416. (in Chinese)

20 段磊, 王国玉, 张敏弟. 绕锥头回转体通气超空化流场结构研究[J]. 兵工学报, 2014, 35(12):2058-2064.

DUAN Lei, WANG Guoyu, ZHANG Mindi. Research on flow field structure of ventilated supercavity around an axisymmetric body[J].Acta Armamentarii, 2014, 35(12):2058-2064. (in Chinese)

21 刘进, 阎兆立, 程晓斌,等. 基于空化辐射噪声的检测方法试验研究[J]. 应用声学, 2014, 33(1):60-65.

LIU Jin, YAN Zhaoli, CHENG Xiaobin, et al. Experiment research on pump cavitation detection based on acoustic radiation[J]. Journal of Applied Acoustic, 2014, 33(1):60-65. (in Chinese)

22 CUDINA M, PREZELJ J. Detection of cavitation in situ operation of kinetic pumps: effect of cavitation on the characteristic discrete frequency component[J]. Applied Acoustics, 2009, 70(9):1175-1182.

23 CUDINA M. Detection of cavitation phenomenon in a centrifugal pump using audible sound[J]. Mechanical Systems & Signal Processing, 2003, 17(6):1335-1347.

24 ZEQIRI B， GELET P N, HODNETT M, et al. A novel sensor for monitoring acoustic cavitation[J].IEEE Transactions on Ultrasonic，Ferroelectrics and Frequency Control，2003，50(10):1342-1350.

25 刘源, 何永勇, 陈大融. 基于小波熵的空化状态检测与识别[J]. 机械强度, 2009, 31(1):19-23.

LIU Yuan, HE Yongyong, CHEN Darong. Wavelet entropy based condition test and identification of cavitation[J]. Journal of Mechanical Strength, 2009, 31(1):19-23. (in Chinese)

26 张俊华, 张伟, 蒲中奇,等. 轴流转桨式水轮机空化程度声信号辨识研究[J]. 中国电机工程学报, 2006, 26(8):72-76.

ZHANG Junhua, ZHANG Wei, PU Zhongqi, et al. Research on the cavitation identification of kaplan turbine using acoustic signals[J]. Proceedings of the Chinese Society for Electrical Engineering , 2006, 26(8):72-76. (in Chinese)

27 戚定满, 沈焕庭. 小波在瞬态空化噪声分析中的应用[J]. 振动与冲击, 2001, 20(1):82-84.

QI Dingman, SHEN Huanting. Wavelet analysis of cavitation noise[J]. Journal of Vibration and Shock, 2001, 20(1):82-84. (in Chinese)

28 卿彪. 基于水下噪声测试对离心泵空化的分析研究[D]. 成都：西华大学, 2015.

QING Biao. Analysis of centrifugal pump cavitation based on underwater noise test[D]. Chengdu:Xihua University, 2015. (in Chinese)

29 冯涛, 刘克, 李晓宏,等. 离心泵水动力噪声测试系统的研制[J]. 流体机械, 2005, 33(4):27-30.

FENG Tao, LIU Ke, LI Xiaohong, et al. Development of the experimental system for measuring the hydrodynamic noise in centrifugal pump[J]. Fluid Machinery, 2005, 33(4):27-30. (in Chinese)

30 KUNZ R F，BOGER D A，STINEBRING D R．A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J]．Computers & Fluids，2000，29(8)：850-872．

31 ZWART P, GERBER A G, BELAMRI T． A two-phase flows model for predicting cavitation dynamics[C]∥ICMF 2004 International Conference on Multiphase Flow, 2004．

32 张炜, 金涛. 流场与声场耦合仿真分析方法及其应用研究[J]. 机械设计, 2015(5):101-104.

ZHANG Wei, JIN Tao.Research on method and application of coupling-simulation-analysis for flow field and sound field of muffler[J]. Journal of Machine Design,2015(5):101-104. (in Chinese)