考虑航天器舱体—附件耦合效应的热颤振准则
2018-01-16樊孝清陆栋宁陈守磊汤亮向志海
樊孝清 陆栋宁 陈守磊 汤亮 向志海†
(1.清华大学航天航空学院, 北京 100084) (2.北京控制工程研究所, 北京 100190)
引言
航天器在进出地球阴影的过程中,太阳翼、天线等轻柔附件受到突变太阳热流的作用会产生热诱发振动现象.这种热致响应可能会干扰航天器平台的姿态,从而影响其正常的功能[1-7].

不稳定的热诱发振动会导致热颤振,从而对航天器产生灾难性的影响.比如,1990年发生的哈勃太空望远镜的太阳翼热颤振事故就严重降低了它的成像精度[1-3].因此,热颤振准则一直是相关领域的研究重点.文献[11]首次建立了悬臂梁的热颤振准则,但随后被文献[12]进行了修正.该准则认为,对于一根受突加热流作用的悬臂梁,只有热流沿着梁表面法线的偏离固定端方向入射时才不会发生热颤振.文献[13]就使用了此准则来分析哈勃太空望远镜的热颤振事故.不过实验发现,当热流沿着悬臂梁法线方向入射时,也会发生热颤振现象[14],和文献[12]的准则不完全一致.而文献[15]认为造成这种差异的原因是忽略了结构受热和变形之间的耦合因素,并给出了一个修正的热颤振准则:只有热流入射角大于热变形后梁端部的转角时才不会发生热颤振.
现有文献中的热颤振准则都是针对一根悬臂梁建立的.但随着航天器的发展,柔性附件的端部往往还会安放有一定质量的科学仪器;而且柔性附件的几何尺寸也越来越大,导致其转动惯量越来越接近航天器舱体的转动惯量.针对这些情况,本文考虑了具有端部附加质量的柔性附件及其和舱体的耦合效应,推导出了一个航天器热颤振准则,并结合有限元模拟讨论了热颤振的一般规律.由于这种结构的振动非常缓慢,因此下面的推导中忽略应变率所产生的热应力.另外,也不考虑材料性能随温度的变化.
1 物理模型和基本方程
1.1 坐标系和基本假设
类似于文献[16],本文讨论如图1所示平面刚柔耦合模型.其中:航天器舱体(质量为M1,转动惯量为I1,回转半径为R1)只发生刚体平移uX、uY和转动β;柔性附件(中面半径为R,壁厚为h的圆管截面梁,其密度为ρ,弹性模量为E、截面惯性矩为I,长度为L,横截面积为A)在随舱体发生刚性转动的同时还发生相对于舱体的弹性变形;外伸端设备(质量为M2,转动惯量为I2,回转半径为R2)和柔性附件是刚性连接,也只发生刚体运动.对此问题可以采用两套坐标系进行描述:
(1)空间固定坐标系X-Y的原点O取为舱体的初始形心.在此坐标系中,太阳热流S0的方向恒定.
(2)随体坐标系x-y的原点o取在舱体和柔性附件梁的连接处.在此坐标系中,梁发生沿着y正方向的弹性变形v.

图1 理论模型Fig. 1 The oretical model
1.2 基本方程
梁上任意一点x处所吸收的热流为:
q(x,φ,t)=αsS0δcosφcos[θ0-θ(x,t)]
(1)
式中:αs为梁表面的吸收率;太阳入射热流和变形前梁法线方向的初始夹角-π/2≤θ0≤π/2;根据Euler-Bernoulli梁的平截面假设,变形后梁法线和变形前梁法线的夹角θ(x,t)=-∂v(x,t)/∂x-β;δ函数描述了梁的一半外表面受热流照射的情况:
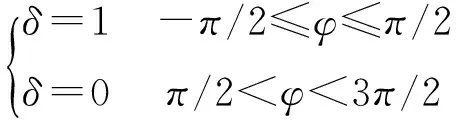
(2)
在此热流作用下,梁中的温度分布满足[15]:
(3)
其中:c是比热,k是导热系数,ε是发射率,σ是玻尔兹曼常数,其值为5.67×10-8W/(m2·K4).
类似于文献[2,3],梁横截面的温度可以近似分解为平均温度Ta和摄动温度Tp两部分:T(x,φ,t)≈Ta(x,t)+Tp(x,t)cosφ.这样,方程(3)可变为两个解耦的方程:
(4)
(5)
Ta只引起梁的长度改变,而Tp会产生分布的热弯矩:
(6)
其中:αT为梁的热膨胀系数.
系统的动能T为柔性附件动能、舱体与外伸端设备的转动动能之和:
(7)
式中Ieff为等效转动惯量:
(8)
系统的势能U只包括柔性附件的势能:
(9)

(10)
(11)
和x=L处的边界条件:
(12)

(13)
1.3 基本方程的稳态解
因为热—固耦合效应对稳态解影响不大[15],下面就求解非耦合情况下的稳态位移.此时令上文方程中和时间相关的项为零,即可求解.
从(4)和(5)式解得稳态平均温度和摄动温度:
(14)
(15)
上式中的热特征时间τT满足:
(16)
从(11)~(13)式可以解得准静态挠度:
(17)

将(17)式代入(10)式可得舱体的稳态转角:

(18)
1.4 基本方程的近似解
柔性附件通常以一阶弯曲振动为主,因此可以将它在随体坐标系中的挠度近似表示为:
v(x,t)=V(t)N(x)
(19)
式中的试函数N(x)=x2,它满足边界条件的要求,即N(0)=0和N′(0)=0.
将(19)式代入(10)~(13)式,用加权余量法可以得到:
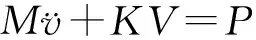
(20)
其中:
(21)
(22)
(23)
由方程(4)和(5)可知Ta比Tp变化缓慢得多,因此可以近似认为它是一个常数.这样(5)式可近似为:
(24)
联立求解(20)~(24)式,就可以得到热—固耦合情况下的近似解.
2 稳定性分析
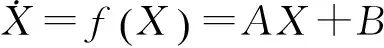
(25)
式中:
(26)
(27)


(28)

(29)

(28)式的特征多项式为:
(30)
其中:

(31)
(32)
(33)
(34)
根据劳斯-赫尔维茨判据,三阶线性系统稳定的充分必要条件是:
(35)
一般舱体的转动惯量都很大,由(34)式可知此时一定满足M>0.根据(32)和(33)式,显然a1>0,a2>0.再根据(31)式,对于常见的柔性附件梁是很容易满足a0>0的.因此只要a1a2>a0系统便是稳定的.根据(31)和(33)式可知,此条件等价于:
(36)
即要求热流的入射角要大于在这个入射角下稳定状态时梁端部的准静态转角.
下面进一步讨论上述稳定性准则:


(3)热颤振准则(36)式是在无阻尼的情况下建立的.阻尼越大,热诱发振动的幅度就会越小.当阻尼大到一定程度时,也不会发生热颤振.
3 仿真校验
当外伸端设备质量很小或对舱体有姿态控制时,可以忽略舱体的转动角,从而认为柔性附件的一端是完全固定的.此时准则(36)就和文献[15]的准则一致,其正确性已经得到验证.

图2 有限元模型Fig. 2 Finite element model

CaseM1/kgI1/kgm2M2/kgI2/kgm2ξ/%θ0/(°)1125.7142.4125.7142.40.002125.7142.4125.7142.40.0603125.7142.4125.7142.40.0-604125.7142.4125.7142.40.205125.7142.4125.7142.40.2606125.7142.4125.7142.40.2-607125.7142.4125.7142.40.808125.7142.4125.7142.40.8609125.7142.4125.7142.40.8-60101256637.11424188.70.00.00.030111256637.11424188.71.01.10.030121256637.11424188.710.011.40.030131256637.11424188.70.00.00.0-30141256637.11424188.71.01.10.0-30151256637.11424188.710.011.40.0-30
下面根据图2所示有限元模型来讨论入射角度θ0、舱体质量特性、设备质量特性和阻尼比ξ对热颤振的影响.该模型中分别用两个“曰”字形刚性方框来模拟舱体和设备(R1=R2=1m),用一根总质量为1.0kg的梁来模拟柔性附件(R=0.01m、h=0.001m、ρ= 2000kg/m3、E=100GPa、k=8W/(m·K)、c=800J/(kg·K)、αs=0.8、ε=0.8、αT=1.610-51/K.模拟时采用文献[2,3]中的有限元方法,考虑了热结构的耦合效应.表1列出了15种工况.施加S0= 1350W/m2的突加阶跃热流时的模拟结果如图3和图4所示.
从图3可以看出,当舱体和外伸端设备的质量特性相同时,无论从何角度入射,系统都是不稳定的.这也不难从系统动能的积累过程进行理解.在没有姿态控制时,系统的空间转动刚度为零,突加热流很容易使其姿态发生改变,从而吸收更多的热量并转化为系统的动能.在没有阻尼时,系统的动能就会越来越大,最终导致系统失稳.这个结论具有普遍性,即当M1和M2不相等时也是成立的.

图3 阻尼和入射角度对舱体转角的影响(M1=M2)Fig. 3 Impact of damping and incident angle on the rotational angle of the hub(M1=M2)
另外从图3还可以看出,施加ξ=0.2%的阻尼可以明显降低热诱发振动的幅值,但还不足以改变系统的稳定性.当阻尼进一步增大到ξ=0.8%时,系统的热诱发振动的幅值急剧衰减,因此整个系统最终也是稳定的.
从图4可以看出,当舱体的质量特性很大时系统就接近于舱体固定的情况,此时的柔性附件就相当于一根带端部质量的悬臂梁,而系统热颤振准则就退化为文献[15]中的结果.另外,如果外伸端设备的质量越大,则系统的弯曲振动频率越低,热诱发振动得就越剧烈.
以上算例的结果和本文推导的热颤振准则所揭示的规律相符.这意味着带柔性附件的航天器在轨运行时如果没有进行姿态控制,在小阻尼情况下是容易发生热颤振的.但在有姿态控制的情况下,可以通过合理的设计来避免发生热颤振事故.

图4 M2对13节点挠度的影响(ξ=0)Fig. 4 Impact of M2 on the deflection of Node 13 (ξ=0)
4 结论
对于含外伸端质量的柔性附件和航天器耦合系统,本文详细推导了其热诱发振动的稳定性准则.该准则得到了有限元结果的验证,并且在舱体质量特性很大时可以退化为已知的热颤振准则.这个稳定性准则以及相关的数值模拟所得到的规律性结果可以为航天器的设计提供帮助.
1 Thornton E A. Thermal Structures for Aerospace Applications. Washington, DC: AIAA, 1996
2 范立佳,段进,向志海等.大型柔性空间结构热-动力学耦合系统的非线性有限元分析. 宇航学报, 2009,30(1):299~304 (Fan L J, Duan J, Xiang Z H, et al. The thermal dynamic coupling analysis of large flexible space structures by finite element method considering geometric nonlinearity.JournalofAstronautics, 2009,30(1):299~304 (in Chinese))
3 薛明德,向志海. 大型空间结构的热-动力学耦合问题及其有限元分析. 固体力学学报, 2011,32(10):318~328 (Xue M D, Xiang Z H. Thermal dynamic coupling problem of large space structures and its FEM analysis.ChineseJournalofSolidMechanics, 2011,32(10):318~328 (in Chinese)
4 Shen Z X, Tian Q, Liu X N, et al. Thermally induced vibrations of flexible beams using absolute nodal coordinate formulation.AerospaceScienceandTechnology, 2013,29(1):386~393
5 Li J L, Yan S Z. Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit.AppliedThermalEngineering, 2014,71(1):419~432
6 Fan L J, Xiang Z H. Suppressing the thermally-induced vibration of large scale space structures via structural optimization.JournalofThermalStresses, 2015,38(1):1~21
7 Zhou Z C, Liu Z S, Qu G J. Modeling on thermally induced coupled micro-motions of satellite with complex flexible appendages.AdvancesInMechanicalEngineering, 2015,7(6):1~7
8 Boley B A. Thermally induced vibrations of beams.JournaloftheAeronauticalSciences, 1956,23(2):179~181
9 Boley B A. Approximate analyses of thermally induced vibrations of beams and plates.JournalofAppliedMechanics,TransactionsoftheASME,SeriesE, 1972,39(1):212~216
10 Su X M, Zhang J H, Wang J, et al. Experimental investigation of the thermally-induced vibration of a space boom section.ScienceChinaPhysics,Mechanics&Astronomy, 2015,58(4):044601
11 Yu Y Y. Thermally induced vibration and flutter of a flexible boom.JournalofSpacecraftandRockets, 1969,6(8):902~910
12 Graham J D. Solar induced bending vibrations of a flexible member.AIAAJournal, 1970,8(11):2031~2036
13 Thornton E A, Kim Y A. Thermally induced bending vibrations of a flexible rolled-up solar array.JournalofSpacecraftandRockets, 1993,30(4):438~448
14 Rimrott F P J, Abdel-Sayed R. Flexural thermal flutter under laboratory conditions.TransactionsoftheCanadianSocietyforMechanicalEngineering, 1977,4(4):189~196
15 Zhang J H, Xiang Z H, Liu Y H. Stability analysis on thermally-induced vibration of a beam subjected to solar heating.AIAAJournal, 2014,52(3):660~665
16 Johnston J D, Thornton E A. Thermally induced attitude dynamics of a spacecraft with a flexible appendage.JournalofGuidanceControlandDynamics, 1998,21(4):581~587
