参数未知的永磁同步电机混沌系统模糊自适应同步控制*
2018-01-16谢成荣张仁愉王仁明王凌云
谢成荣 张仁愉 王仁明 王凌云
(1.国家电网公司 浙江嵊州市供电公司,嵊州 312400) (2.三峡大学电气与新能源学院, 宜昌 443002)
引言
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)由于其结构简单、运行可靠、无励磁损耗等优点而广泛应用于航空航天、工业自动化装置、机器人、家用电器等领域,但其动力系统是一种复杂的多变量、强耦合的高维非线性系统.PMSM在一些特定的参数和工作条件下会呈现混沌行为[1],表现为转矩和转速的间歇振荡和不规则的电磁噪声等.PMSM的混沌运动会影响电力传动系统的稳定性,降低系统的运行性能,因此,PMSM混沌行为的控制具有非常重要的现实意义和实用价值[2].
现代非线性控制理论的发展出现了许多控制和分析混沌系统的方法[3-7],一些方法也被用于控制PMSM的混沌行为[8-11,13].例如,基于逆最优控制方法的线性反馈控制器设计[8]、基于哈密尔顿函数的鲁棒控制方案[12]、基于PMSM分数阶混沌吸引子的投影自同步非线性状态观测器控制策略[13]和基于反演技术的自适应模糊同步控制器设计方法[14]等.
模糊控制和自适应控制是两种被广泛使用于控制混沌系统的方法[6,14-17].模糊控制方法的优越性是T-S模糊模型能够精确地表示一类高度非线性模型的特性.这种模糊模型在不同的状态空间区域的局部动态能够被表示为线性模型,然后通过这些线性模型的模糊综合得到整个非线性系统模型.从而可以利用线性系统的分析方法研究混沌系统.文献[18]研究了基于模糊模型的未知参数混沌系统的自适应同步控制方法.混沌系统由驱动系统和响应系统组成,T-S模糊模型用来表示混沌系统,自适应律被设计用于未知参数的估计.而文献[6]则基于自适应鲁棒控制方法,设计了不确定混沌系统的输出反馈控制.文献[4]提出了基于反演技术的自适应模糊神经控制方法,用于分析一类输入饱和的未知混沌系统的镇定问题.文献[15]则给出了模糊滑模控制设计方法来改进不确定混沌系统的鲁棒性和稳定性.文献[17]建立了不确定混沌系统的动态模糊神经网络模型并设计了神经自适应反演控制器.
混沌的同步研究起源于Carroll和Pecora关于两个混沌系统同步控制的开拓性工作[2],随后,研究者对此进行了大量的研究,提出了许多混沌同步方法,如驱动-响应同步法[2]、自适应模糊同步法[18]、脉冲同步法[19]、完全与反相同步法[23]等.例如,文献[23]研究了分数阶异结构混沌系统的完全同步和反相同步控制问题,构造出非线性控制器实现了两个维数不同、分数阶次不等的混沌系统与超混沌系统之间的完全同步与反相同步.其中一些方法也被用于PMSM的混沌同步控制问题研究[13,20].
本文利用模糊控制与自适应控制策略相结合的优点,提出了一种基于T-S模糊模型的永磁同步电机(PMSM)混沌系统的自适应同步控制方法.首先建立了驱动系统和响应系统的T-S模糊模型,并由此导出了同步误差动态,设计了模糊控制器并进行了稳定性分析.同时,由驱动系统状态和响应系统状态之间的误差构造了响应系统控制律,使之达到渐近同步.而为了估计驱动系统的未知参数,进一步构造了响应系统的自适应律.响应系统的控制器设计有两部分组成:一部分用于镇定同步误差,而另一部分用来估计未知参数,且由Lyapunov理论分析了所设计的控制系统的稳定性.
1 PMSM的数学模型
在转子磁场定向坐标系(d-q坐标系)中,由电压平衡方程和转矩平衡方程,可得如下的PMSM状态方程[1]:
(1)
其中ud,id,Ld和uq,iq,Lq分别表示直轴和交轴的定子电压向量、定子电流向量和电感向量分量,Rs是定子电阻,np是极对数,J是转子惯量,b是阻尼系数,TL是负载转矩,ωr为转子角速度,φ为转子永久磁链.
考虑气隙均匀的PMSM,即Ld=Lq=L.此时,系统(1)可写为:
(2)
通过仿射变换和时间尺度变换,将系统(2)变成无量纲方程,令:

选择仿射变换及时间尺度变换为:
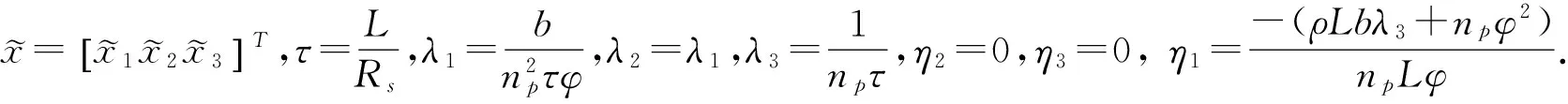
(3)

2 PMSM的混沌动态分析
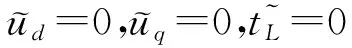
Jacobian矩阵对应的特征多项式为:
(4)

图1 PMSM的奇怪吸引子Fig. 1 Chaos attractor of PMSM
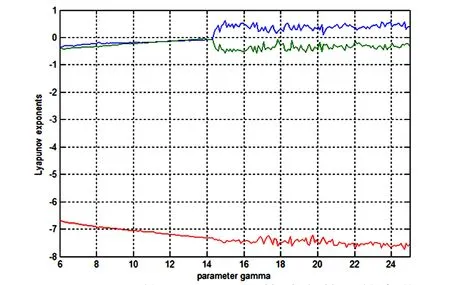
图2 PMSM的Lyapunov指数随参数γ的变化 Fig. 2 Evolution of Lyapunov exponent with the parameter γ
3 PMSM混沌系统的T-S模糊自适应同步
对于PMSM系统同步问题,其响应系统状态应被设计为与PMSM系统状态相同.因此,驱动系统(PMSM)被模糊表示如下:
驱动系统规则i:
IFz1(t) isMi1,…,zp(t) isMipTHEN
(5)
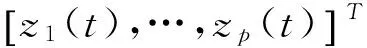
(6)
其中:
根据模糊驱动系统,可得如下模糊响应系统:
响应系统规则i:
IFz1(t) isMi1,…,zp(t) isMipTHEN
(7)

(8)
(9)

为了镇定同步误差动态系统(9),设计状态反馈控制律和自适应律如下:
控制规则i:
IFz1(t) isMi1,…,zp(t) isMipTHEN
这里,As为任一Hurwitz稳定矩阵.经过模糊推理,整个模糊控制器可表示为:
(10)
假设自适应律可表示为:
(11)
这里,σAi为常数自适应增益.由(9)和(10)得到闭环同步误差动态为:
(12)

选择Lyapunov函数为:
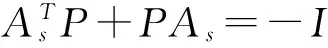
由(11)可知:
(13)
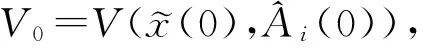
注:上述结论是在气隙均匀的假设下,对PMSM系统进行分析和设计得到的,在非气隙均匀情形,即Ld≠Lq时,文献[20]应用自适应控制方法研究了这种情形的同步问题.本文提出的方法也可以应用于非气隙均匀情形.这个问题的讨论将在另外文献中表述.
4 数值仿真

仿文献[21]的建模过程,建立PMSM的T-S模糊模型.假设参数σ,γ未知,由于:

这里g1(x(t))=M1=-20;g2(x(t))=M2=20.并且:
(14)
由图1可知x3(t)∈[-20, 20],所以选择M1=-20,M2=20,于是得到如下驱动系统的模糊T-S模型.


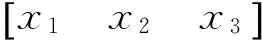

响应系统的模糊T-S模型可描述为:
规则1:
规则2:
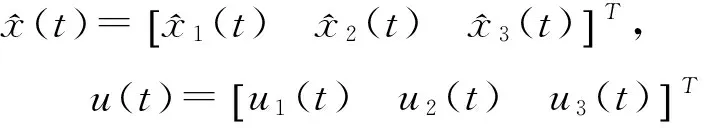
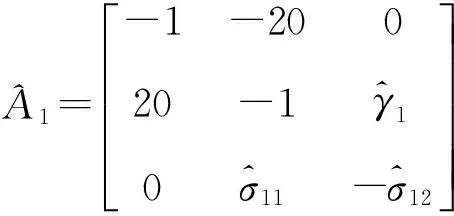

通过求解Lyapunov方程可得:

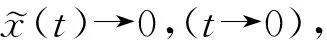

图3 PMSM驱动系统和响应系统状态轨迹(a)x1(t)和和和Fig. 3 State trajectory of PMSM systems(a)x1(t) and (t); (b)x2(t) and (t); (c)x3(t) and (t)
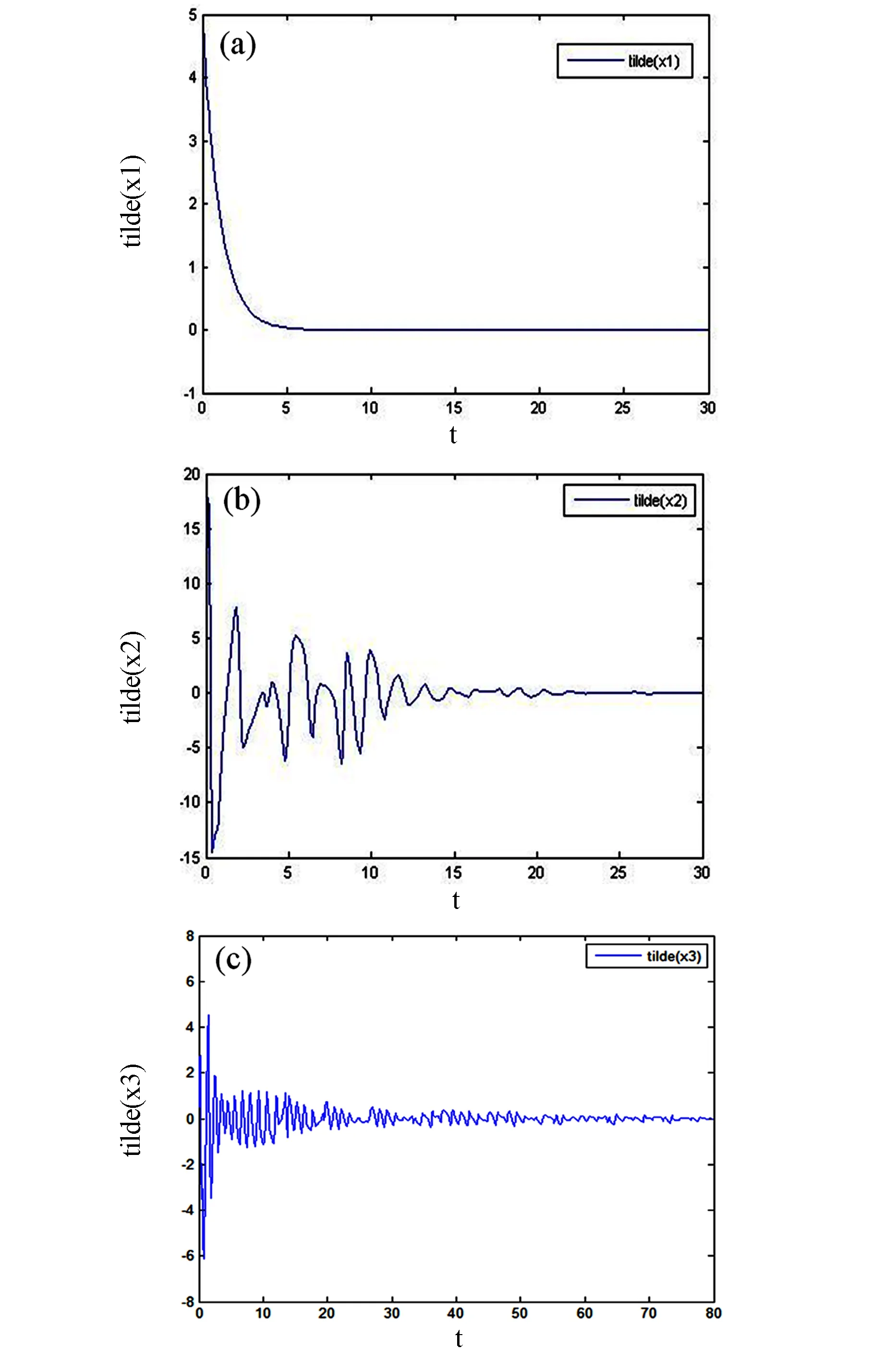
图4 PMSM混沌系统的同步误差Fig. 4 Synchronization error of PMSM attractor
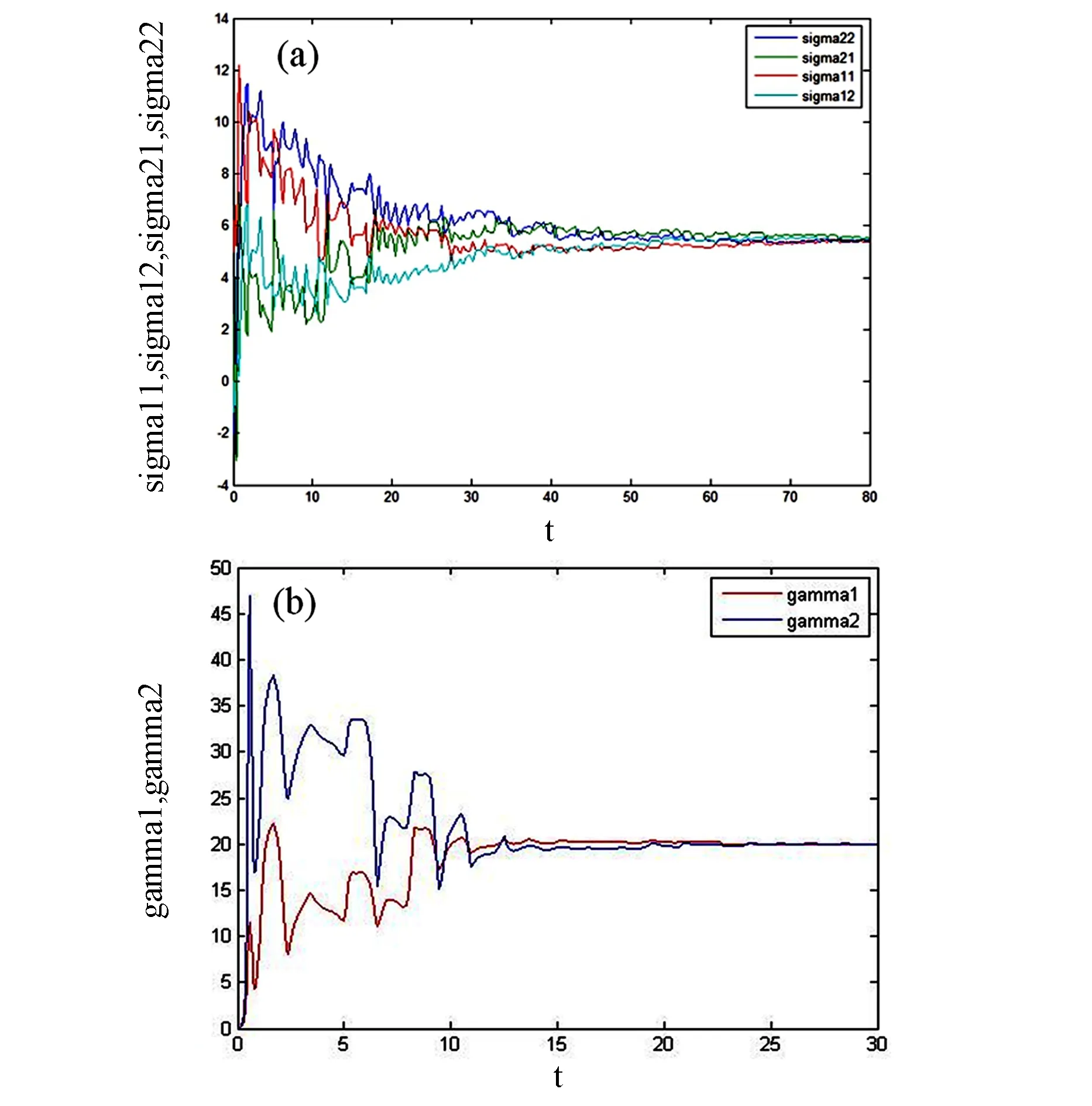
图5 PMSM系统的参数估计Fig. 5 Parameter estimation for PMSM attractor
5 结论
本文提出了一种永磁同步电机(PMSM)混沌系统的模糊自适应同步控制方法.在假设驱动系统(PMSM混沌系统)参数未知的情形下,T-S模糊模型被用来描述驱动系统和响应系统,通过对驱动系统参数的估计设计了模糊响应系统并通过模糊控制器的设计使得同步误差动态渐近稳定.数值仿真验证了所提出的自适应同步方案的有效性.
1Hemati N. Strange attractors in brushless DC motors.IEEETransactiononCircuitsandSystems, 1994,41(2):40~45
2Pecora L M, Canoll T L. Synchronization in chaotic system.PhysicalReviewLetters, 1990,64(8):821~824
3Ricalde L J, Sanchez E N. Inverse optimal neural control of a class of nonlinear systems with constrained input for trajectory tracking.OptimalControlApplicationsandMethods, 2012,33(2):176~198
4Lin D, Wang X Y, Yao Y. Fuzzy neural adaptive tracking control of unknown chaotic systems with input saturation.NonlinearDynamics, 2012,67(4):2889~2897
5王兴元. 复杂非线性系统中的混沌. 北京:电子工业出版社, 2003 (Wang X Y. Chaos in the complex nonlinear system. Beijing: Electronics Industry Press, 2003 (in Chinese))
6Liu Y J, Zhang Y Q. Adaptive robust fuzzy control for a class of uncertain chaotic systems.NonlinearDynamics, 2009,57(3):431~439
7Liu Y J, Wen G X, Tong S C. Adaptive neural output feedback tracking control for a class of uncertain discrete-time nonlinear systems.IEEETransactiononNeuralNetworks, 2011,7(22):1162~1167
8Wei Q, Wang X Y, Hu X P. Inverse optimal control for permanent magnet synchronous motor.JournalofVibrationandControl, 2015,21(4):801~807
9Zribi M, Oteafy A, Smaoui N. Controlling chaos in the permanent magnet synchronous motor.Chaos,Solitons&Fractals, 2009,41(3):1266~1276
10 Liu B C, Lue Y F. Dither signal effects on quenching chaos of permanent magnet synchronous motor in electric vehicles.JournalofVibrationandControl, 2011,17(12):1912~1918
11 Wei W, Zou M, Jiang T Q, et al. Control chaos in permanent magnet synchronous motors by cascade adaptive approach.AppliedMechanicsandMaterials, 2011,96(10):128~129
12 吴忠强,吴昌韩,赵立儒等. 基于哈密顿函数的永磁同步电机混沌系统的鲁棒控制. 物理学报, 2015,64(9):090503 (Wu Z Q, Wu C H, Zhao L R, et al. Robust control for permanent magnet synchronous motors based on Hamiltonian Function.ActaPhysicaSinica, 2015,64(9):090503 (in Chinese))
13 Liu L, Liang D L, Liu C X, et al. Nonlinear state observer design for projective synchronization of fractional-order permanent magnet synchronous motor.InternationalJournalofModernPhysicsB, 2012,26(30):1250166-1~1250166-16
14 Yu J P, Chen B, Yu H S, et al. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping.NonlinearAnalysis:RealWorldApplication, 2010,1(12):671~681
15 Niu Y J, Wang X Y. A novel adaptive fuzzy sliding-mode controller for uncertain chaotic systems.NonlinearDynamics, 2013,73(3):1201~1209
16 Lin D, Wang X Y. Self-organizing adaptive fuzzy neural control for the synchronization of uncertain chaotic systems with random varying parameters.Neurocomputing, 2011,74(12-13):2241~2249
17 Lin D, Wang X Y, Nian F H, et al. Dynamic fuzzy neural networks modeling and adaptive backstepping tracking control of uncertain chaotic systems.Neurocomputing, 2010,73(16-18):2873~2881
18 Kim J H, Park C W, Kim E, et al. Adaptive synchronization of T-S fuzzy chaotic systems with unknown parameters.Chaos,Solitons&Fractals, 2005,24:1353~1361
19 陈菊芳,张入元,彭建华. 脉冲驱动离散混沌系统同步的实验与理论研究. 物理学报, 2003,52(7):1589~1594 (Chen J F, Zhang R Y, Peng J H. Experimental study for impulsive synchronization of a discrete chaotic system.ActaPhysicaSinica, 2003,52(7):1589~1594 (in Chinese))
20 张兴华,丁守刚. 非均匀气隙永磁同步电机的自适应混沌同步. 控制理论与应用, 2009,26(6):661~664 (Zhang X H, Ding S G. Adaptive chaotic synchronization of permanent magnet synchronous motors with non-smooth air-gap.ControlTheory&Applications, 2009,26(6):661~664 (in Chinese))
21 Tanaka K, Ikeda T, Wang H O. A unified approach to chaos via an LMI-based fuzzy control system design.IEEETransactionsonCircuitsandSystem1:FundamentalTheoryandApplications, 1999,45(10):1021~1040
22 张兴华,王德明. 永磁同步电机与异结构系统的混沌同步控制. 系统仿真学报, 2009,21(14):4467~4474 (Zhang X H, Wang D M. Chaos synchronization control between permanent magnet synchronous motors and different systems.JournalofSystemSimulation, 2009,21(14):4467~4474 (in Chinese))
23 董俊,张广军,姚宏等. 分数阶异结构超混沌系统完全同步与反相同步控制. 动力学与控制学报, 2014,12(2):119~126 (Dong J, Zhang G J, Yao H, et al. The control of complete synchronization and anti-phase synchronization for fractional-order hyper-chaotic systems of different structures.JournalofDynamicsandControl, 2014,12(2):119~126 (in Chinese))
