基于改进等效电流量测变换的状态估计算法

孟德军, 樊汝森, 杨小立, 王 勇

(1.上海电力学院, 上海 200090; 2.国网浙江省电力公司检修分公司, 浙江 杭州 311232;3.国网上海市电力公司青浦供电公司, 上海 200122)

现代电力系统的安全可靠运行离不开能量管理系统(Energy Management System,EMS),EMS是电网调度的核心,而状态估计是EMS中不可缺少的组成部分[1].状态估计是电力系统后续数据处理和在线分析的基础,如果状态估计所得出的结果不准确,会直接影响后续的计算分析.自从20世纪70年代美国麻省理工学院的SCHWEPPE F C等人[2-4]提出了基本的加权最小二乘法状态估计后,经过多年的发展,状态估计算法已经逐渐完善.

针对输配电系统量测类型多样性的特点,文献[5]提出了一种基于等效电流量测变换的状态估计算法,此方法具有收敛速度快、估计精度较高的特点.本文将在此方法的基础上应用抗差估计理论[6]的思想,构造出一组权函数来修正等效电流量测变换法的权重,达到提高估计精度的目的.

1 等效电流量测变换算法

1.1 量测量的等效变换

量测量主要包括节点注入有功功率Pi,m,节点注入无功功率Qi,m,支路有功功率Pij,m,支路无功功率Qij,m等.这些量测量可以通过等效量测变换,变换成节点型电流量测量Ii,m,ep或者支路型电流量测量Iij,m,ep.

节点注入有功功率和无功功率量测量可以等效变换成[5]:

(1)

式中:ei,fi——直角坐标形式下第i个节点电压向量的实部和虚部.

同理,支路有功功率和无功功率的量测量可以等效变换成[5]:

(2)

1.2 数学模型

量测方程为:

z=h(x)+v

(3)

式中:z——m维量测向量;

x——n维状态向量;

h——量测函数;

v——对应的m维量测误差向量.

状态估计问题可以表述为使得下列目标函数取得最小值:

J(x)=[z-h(x)]TR-1[z-h(x)]

(4)

式中:R-1——量测量的权重矩阵.

非线性目标函数的迭代方程为:

[HTR-1H]Δx=HTR-1[z-h(x)]

(5)

式(5)中,H=∂h(x)/∂x,称为量测雅可比矩阵,HTR-1H称为信息矩阵.

经过等效变换后,等效节点电流和等效支路电流的量测函数Ii,cal和Iij,cal分别为:

(6)

雅可比矩阵等效变换为:

(7)

式中:IRe,IIm——等效电流的实部和虚部;

ei,fi——状态估计电压的实部和虚部;

G——电导的矩阵;

B——电纳的矩阵.

信息矩阵等效变换为:

HTR-1H=

(8)

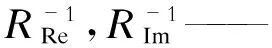
同样可推出:

HTR-1[z-h(x)]=

(9)

2 算法改进

2.1 等效电流的量测权重

在状态估计的过程中,等效变换后的电流量测权重应不同于原来量测量对应的权重.文献[6]提出了间接量测的误差传递规律.

(10)

由式(1),式(2)和式(10)可求得等效电流量测变换后的权重.

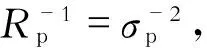
(11)

(12)

实际上,在等效变换后,等效电流的权重主要由量测量的方差决定.对于不同的量测量来说,方差一样则等效变换前一般取相同的权重,等效变换后的权重近似相等.但是这两个量测量的相对标准差(标准差/量测量)却相差很多,而且在每次状态估计中,量测量与真值的差值总是与标准差有一定的偏离,因此在状态估计中取相同或近似相同的权重是有待改进的.

2.2 修正权重

抗差估计理论就是在有粗差的情况下,尽可能选择好的估计方法,从而减少粗差的影响,得到正常情况下的最佳估计.抗差估计主要有M估计,L估计和R估计.本文将采用M估计的方法构造出一组恰当的权函数来修正权重,通过对权重的处理使得残差绝对值大的量测量的权重逐渐变小,从而得到更为精确的估计值.

利用M估计的思想构造的一组权函数为:

(13)

式中:m,n——0～1之间的常数;

3 算例仿真与分析

利用Matlab软件对IEEE14节点系统进行仿真实验.IEEE14节点系统结构如图1所示.

图1 IEEE14节点系统结构示意

量测系统的量测对象包含节点电压幅值、节点电压的相角、注入有功功率和无功功率、支路有功功率和无功功率.以潮流计算的结果作为系统的真值,将真值叠加期望为0,标准差为0.01的白噪声作为系统的量测值进行状态估计.所有量测值均用标幺值表示.功率基准值为100 MW;状态量为所有电压和相角,初始电压为1,相角为0.初始权重取量测误差的方差倒数,收敛判据为计算结果误差小于10-6.

等效电流量测变换法改进前后的状态估计结果与误差如表1所示.为了便于与真实值对比,其结果由直角坐标变换为极坐标表示.

图2为两种算法的电压幅值和电压相角与其真实值的对比图.图3为改进算法前后的电压幅值和电压相角误差对比图.

表1 算法的估计结果

图2 算法改进前后与真实值的对比曲线

由表1可以看出,算法改进后的估计结果更接近真实值.图2通过直观对比更形象地说明了这一点.由图3可以看出,算法改进后的电压幅值和电压角度误差更接近于零,这说明算法改进后的估计精度得到了提高.表2为改进算法后的电压幅值和电压角度精确度提高百分比.

图3 算法改进前后的误差曲线

从表2可以看出,改进算法后电压幅值的精确度平均提高了0.23%,电压角度的精确度平均提高了0.48%.

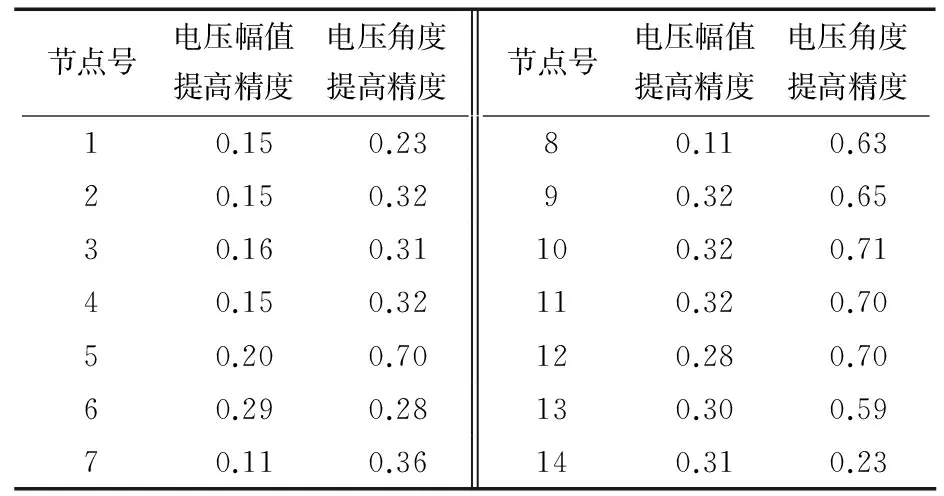
表2 改进算法后精确度提高的百分比 %

4 结 语

本文在等效电流量测变换算法的基础上提出了一种改进算法,根据抗差估计理论构造了一个权函数,在每次迭代的过程中对权重进行不断修正.仿真实验表明,与原算法相比,改进后的算法的估计精度得到了提高.

[1] 兰华,李积捷.电力系统状态估计算法的研究现状和展望[J].继电器,2007,35(10):78-82.

[2] SCHWEPPE F C,WILDES J.Power system static-state estimation,PartI:exact model[J].IEEE Transactions on Power Apparatus and Systems,1970,89(1):120-125.

[3] SCHWEPPE F C,ROM D B.Power system static-state estimation,PartII:approximate model[J].IEEE Transactions on Power Apparatus and Systems,1970,89(1):125-130.

[4] SCHWEPPE F C.Power system static-state estimation,Part III:implementation[J].IEEE Transactions on Power Apparatus and Systems,1970,89(1):130-135.

[5] 程浩中,袁青山,汪一华,等.基于等效电流量测变换的电力系统状态估计方法[J].电力系统自动化,2000,24(14):25-29.

[6] 杨元喜.抗差估计理论及其应用[M].北京:八一出版社,1993:23-27.