基于TransCAD的BPR路阻函数对OD反推影响分析

程浩+朱从坤

摘要： 随着交通信息采集技术的发展，路段流量的获取变得越来越容易。因此，通过路段观测流量来反推OD矩阵的方法成为一种经济实用的方法。本文介绍了基于TransCAD软件OD矩阵反推的方法，并结合苏州市部分特定路网建立了路网模型。运用单因素敏感性分析法，结合选定的均方根误差、相对误差以及模态置信准则（MAC）等三个评价指标，分析BPR路阻函数参数α和β对OD矩阵反推结果精度的影响。在反推过程中建议使用随机用户平衡分配法（SUE），并给出α和β的建议取值范围，可为提高利用TransCAD软件进行OD矩阵反推精度提供参考。

Abstract： With the development of traffic information collection technology， the acquisition of road traffic becomes easier. Therefore， it is an economical and practical method to inverse OD matrix by observing the flow of traffic on each link. In this paper， the method of OD matrix inversion based on TransCAD software is introduced， and the road network model is established based on some specific road networks in Suzhou. By using single factor sensitivity analysis and combining with three selected evaluation indexes such as root mean square error， relative error and modal confidence criterion （MAC）， the influence of parameters α and β of the BPR function on the precision of the OD matrix is analyzed. In the process of inversing， it is recommended to use the SUE （Random Balanced User Allocation） method and give the suggested values of α and β， which can provide reference for improving the accuracy of OD matrix using TransCAD software.

關键词： TransCAD；反推OD矩阵；BPR路阻函数；影响分析

Key words： TransCAD；inverse OD matrix；BPR resistance function；effect analysis

中图分类号：U491 文献标识码：A 文章编号：1006-4311（2018）01-0205-04

0 引言

机动车OD矩阵直接反映路网中的车流在空间上的分布状况，是区域机动车交通需求预测的基础数据。机动车OD的获取方法有两种，一种是通过大规模的抽样调查获取；另一种是通过路段流量反推OD矩阵，该方法相对第一种方法省时、省力且耗资少。TransCAD软件中提供了OD矩阵的反推模块，实现了OD矩阵反推的可操作性。路阻函数是影响OD反推精度的重要建筑工程自动化供配电系统因素，本文利用TransCAD软件中的OD反推模块，结合苏州部分特定路网，分析BPR路阻函数中参数的设置对OD反推精度的影响，以期获得反推OD矩阵精度较高时所对应的参数取值范围，为交通规划、管理提供相应的指导。

1 TransCAD中的反推OD过程简介

TransCAD软件是一款用于交通数据管理、分析的专业交通规划软件，其内部程序基于路网路段上调研的样本计数以及可被选择的初始出行OD矩阵可以更精准地推算并更新起迄点之间的OD出行矩阵。运用TransCAD软件反推OD矩阵的过程中，必须把一个初始OD矩阵视为起点进行推算，最后在设定好的内外循环次数内反复进行交通分配并反复反推OD矩阵，得到的推算结果如果达到了收敛条件的相关要求，即刻输出最终的OD矩阵。目前主要采用两种矩阵反推方法，一是单一路径反推，二是多路径反推。TransCAD软件进行OD矩阵反推得到OD矩阵的同时，也会通过交通分配得到路网中各路段的分配交通流量。

TransCAD软件中OD矩阵反推的流程及数据准备如图1所示。

OD矩阵中的核心步骤之一是交通分配方法的选取，通过对比分析，本文选取随机用户平衡法作为交通分配的方法，其中，影响出行路径选择的因素是各条道路的阻抗函数。

2 美国BPR路阻函数

交通阻抗是车辆在路段运行中所遇到阻力大小的量值。广义的路阻是人、车、路三方面因素对交通出行的阻力作用。狭义的路阻是车辆出行在道路上花费的行程时间。本文的路阻函数为狭义的路阻函数。目前，国内外使用较广泛的是美国BPR阻抗函数，其公式表达如下：

式中：va—路段a的交通量；

Ca—路段a的通行能力；

？琢、？茁—为可调系数；

ta（va）、ta（0）—交通量分别为va和自由流时，路段a的行程时间。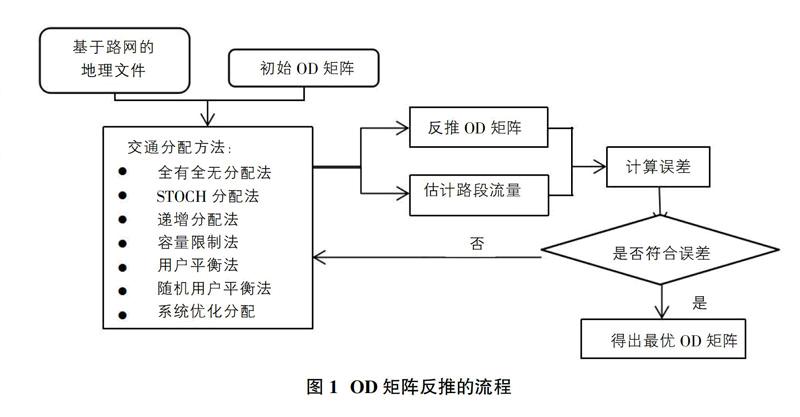

在国外研究中一般取？琢=0.15，？茁=4.0。因为国内与国外的道路状况有较大的差异，且？琢和？茁的取值会直接影响OD反推的结果，为此需对和的合理取值范围进行分析。endprint

3 实际案例

在此选取苏州市部分特定路网进行实例分析。该路网包含了不同的道路类型，比较具有代表性。在TransCAD软件上建立路网模型（见图2），包含16个交通小区和155条路段。本项目设置了5个OD调查点，分别是：312国道苏州东出口（外跨塘路段）、312国道苏州西出口（望东路至绕城高速段）、227省道胡巷段、苏虞张公路莫阳段、苏嘉杭高速公路太平互通出入口处。调查路段交通量时需要事前布置调查断面共计27个，调查交叉口处的交通量时需要采集312国道与S227分流线交叉口、312国道与望东路交叉口、苏虞张公路与太阳路交叉口、227省道与太阳路交叉口4个交叉口的交通量樣本，按照既定的方向和车型，逐一展开为期12小时的调查。

根据OD矩阵反推模型的需要，建立相应路段的属性，包括路线名称、里程、路段两个方向的观测交通量。

通过调查数据可以获取路段观测流量，但无法获取初始OD矩阵，所以定义初始OD矩阵数据统一填“1”，其他参数设置为默认。

4 实验方案设计及影响分析

4.1 方案设计

本文主要研究BPR路阻函数中，参数？琢、？茁的变化对反推OD结果的影响程度。

①将路网中道路根据通行能力大小分为三类，分别设置参数可提高OD反推的精度。第一类道路单向通行能力未能达到1200veh/h；第二类道路单向通行能力在1200～2500veh/h之间；第三类道路单向通行能力在2500veh/h以上。

②对路阻函数中参数？琢、？茁值进行初步标定，反推得出基准OD矩阵作为反推结果比较的基准。BPR路阻函数设定？琢和？茁的参考值分别是0.15和4.0，该参考值仅适用于美国路网建设要求，在中国必须重新标定？琢和？茁的参考值，并且要在实际应用中针对不同的道路类型对给定的参考值进行合理调整，以确保参考值更加精准，更充分地满足路网建设要求。

重新标定路段阻抗函数参数值时，先根据下式对BRP函数公式两边取对数：

ln■-1=lna+？茁ln■（2）

其中：ta（qa），ta（0），qa，Ca，可以从调查中得到；设

ln-1=Y，ln ？琢=c，ln=X，？茁=k（3）

根据上式得到Y=kX+c 。在该运算方程中，X为因变量，Y为自变量，基于路段属性数据可以得到X与Y的取值，然后通过Excel一元回归最终得到 k、c的取值，再通过“？琢=ec，？茁=k”得到待标定参数？琢、？茁的具体数值（详见表1）。

③调整参数？琢、？茁的值，得出不同的反推OD矩阵和各路段流量。

④对反推得出的结果进行影响分析。分析可分为两大类：1）反推出的OD矩阵的影响分析；2）路段分配交通量的影响分析。选定的分析评价指标有均方根误差、平均相对误差和模态置信准则（MAC）。

a）均方根误差（RMSE）

式中：t—第w对OD出行量的真实值；

t—第w对OD出行量的估计值；

wn—OD对数。

该指标检验反推OD矩阵，均方根误差的值越小，表示精度越高。

b）平均相对误差（MRE）

MRE=×100%（5）

在式（5）中，qk表示“路段分配流量”；vk表示“路段实际观测流量”。这项指标主要用于对路段分配流量的检验，相对误差平均值越小，反推精度越高。

c）模态置信准则（MAC）

模态置信准则（MAC）是评价模态向量交角的一种数学工具，同时也可以比较两个向量之间相似度。公式为：

MAC（A，B）=（6）

在式（6）中，A表示“向量中的估计值”；B表示“向量中真实值”；T表示“矩阵的转置。这项指标主要用于对OD矩阵相似性的分析，MAC取值为0～1，取值与1越接近，两组数据关联越紧密。

4.2 影响分析

4.2.1 均方根误差指标分析

在实验过程中，其它设置值恒定不变，按照基础标定的数值确定的取值范围，即0～5.6，间隔为0.2，确定？茁的取值范围，即0～10，间隔同上。综合分析道路类型的过程中，只调整一个参数展开分析，比如对第一类道路的参数？琢进行调整计算时，确保第一类道路的？茁的值不变，其它类型的道路α、β的取值也恒定不变，取参数基础的标定值作为计算值。图3和图4为α、β取值下，反推OD矩阵的均方根误差的变化情况。

从图3可以看出，第一、二、三类道路的？琢值分别取在1.4～2.5、2～3、3～4.8之间时， OD矩阵的均方根误差最小，并且误差变化比较平稳，精度较高。

从图4可以看出，第一、二、三类道路的β值分别取在5.6～7、4.7～6.1、4～5.3之间时， OD矩阵的均方根误差最小，并且变化趋势比较平稳，精度较高。

4.2.2 平均相对误差指标分析

路段分配流量的平均相对误差随α、β变化的情况如图5、图6所示。

从图5可以看出，第一、二、三类道路的？琢值分别取1.4～2.6、2.3～3.4、2.5～4.1之间时，所有路段分配流量的平均相对误差最小，并且变化趋势比较平稳，精度较高。

从图6可以看出，第一、二、三类道路的β值分别取5.5～7.2、5.2～7.2、5.2～7之间时，所有路段分配流量的平均相对误差最小，并且变化趋势比较平稳，精度较高。

4.2.3 模态置信准则（MAC）指标分析

反推OD矩阵的模态置信准则随α、β变化的情况如图7、图8所示。

从图7可以看出，第一、二、三类道路的？琢值分别取1.4～3.4、2.5～3.4、2.2～4.3之间时，整个OD矩阵的相似性最大，并且变化趋势比较平稳，精度较高。

从图8可以看出，第一、二、三类道路的β值分别取5.2～7.3、4.4～6.5、4.6～6.7之间时，整个OD矩阵的相似性最大，并且变化趋势比较平稳，精度较高。

5 结语

本文应用TransCAD软件，结合苏州市部分特定路网进行OD矩阵反推。运用单因素敏感性分析的方法，选定均方根误差、相对误差以及模态置信准则三个指标评价反推精度。分析了反推OD矩阵和路段分配交通量的评价指标随路阻函数参数α和β的变化情况。结果表明，在进行OD矩阵反推时，建议采用随机用户平衡分配法（SUE），基于这种交通分配模式，根据表2确定路阻函数参数？琢、？茁的取值范围。可见，基于这种分配模式以及在该模式下确定的路阻函数参数值的取值范围内矩阵反推精度更高。

参考文献：

[1]刘灿齐.现代交通规划学[M].北京：人民交通出版社，2001：206-283.

[2]郑远，等.美国联邦公路局路阻函数探讨[J].交通与运输，2007（7）：24-26.

[3]邓建华.道路交通系统仿真技术与应用[M].北京：国防工业出版社，2013：123-132.

[4]易昆南，李志纯.由路段交通量推算OD矩阵的一种有效方法及其应用[J].运筹与管理2002，11（5）：65-70.

[5]闫小勇，刘博航.交通规划软件实验教程[M].北京：机械工业出版社，2010：64-75.endprint