校园考试分数保险保费厘定

魏凡伟+高溪远+乔霂源+易禹妍

【摘要】本文针对当代大学生关心的考试成绩问题，利用校内考试成绩资料及B-S期权定价模型量化地给出了具有绝对免赔额形式下的考试分数保险的保费厘定方法，并进一步利用蝶式差价构建了针对不同考试分数的对应赔偿方案，以期在校园保险等小险种费率厘定的探索中做出一定的尝试.最后，我们结合考生历年期末成绩，对该保险的保费进行了模拟.

【关键词】考试分数保险；费率厘定；B-S期权模型；蝶式差价

一、引 言

（一）研究背景

保险（Insurance），本意是稳妥可靠，后延伸成一种保障机制，是用来规划人生财务的一种工具.纵然当前我国保险市场发展迅速，但在针对校内意外事件开发险种方面，国内市场却几乎一直处于空白状态.这主要由于可保风险一般为纯粹风险，满足不可抗拒原则和补偿原则，且应能有效防止逆向选择[1]，而考试未通过不属于纯粹风险且若给予承保，亦难以规避逆向选择.

当前，保险定价常用的模型包括损失期望理论、期望效用理论、资本资产定价模型（CAPM）等.本文希望使用期权定价中的B-S模型对保险费率厘定进行探讨.

二、费率计算理论

在对大学生的走访中，我们发现大学生群体普遍最为关注的风险是可能发生的考试不及格及其對自身长期发展带来的负面影响.进一步讨论中，我们发现针对考试分数设计保险产品相较于其他校园意外事件具有覆盖范围广、受关注程度高、易量化分析等天然优势.故本文以基于考试分数的保险为对象，应用数理方法对该保险产品的开发进行费率厘定和数值分析方面的尝试.

我们认为该保险费率的厘定应以损失概率为基础，即先通过对保额损失率和均方差的计算求出纯费率，之后计算附加费率并将两者加和得到毛保险费率.

在本挂科险中，我们假定本校考试未通过后补考费用为每学分50元，以实变函数（4学分）课程为例，则考试未通过带来的经济损失为200元.在衡量精神损失时，我们将由挂科所产生的精神损失费设为每学分补考费的8%，6%，4%，2%，具体百分比p可由投保人自行决定，并将反映在最终的保费厘定中.综上，该挂科险最高赔付金额应为200（1+p）元.

四、应用实例

为了验证本文方法的实用性，我们收集了本校数学学院2014级全体本科生的数学分析、高等代数、实变函数等10门专业课成绩作为样本，计算出各样本总体的数字特征，并针对实变函数科目进行考试分数保险产品的模拟投放和数据分析.以实变函数成绩为例，样本数量共计276个.

首先假定投保人在投保后至考试这段时间内，在任意时刻t+Δt的成绩St+Δt随时间变化且服从对数正态分布.在计算投保费用c时，我们需要预确定投保人投保时学习状态St，常用的方法主要有下述两种：我们既可以安排投保人进行一次该科目的水平测试，以其当次测试成绩作为投保人初始学习状态St；也可以根据该投保人历年期末考试成绩，合理推断其当前学习状态.第一种方法手续较为复杂，但能在更大程度上反应投保人投保时刻的真实水平；第二种方法则可看作第一种方法的简化手段.由于第二种方法操作过程明确，我们在此主要讨论以其历年成绩代替St的方法.

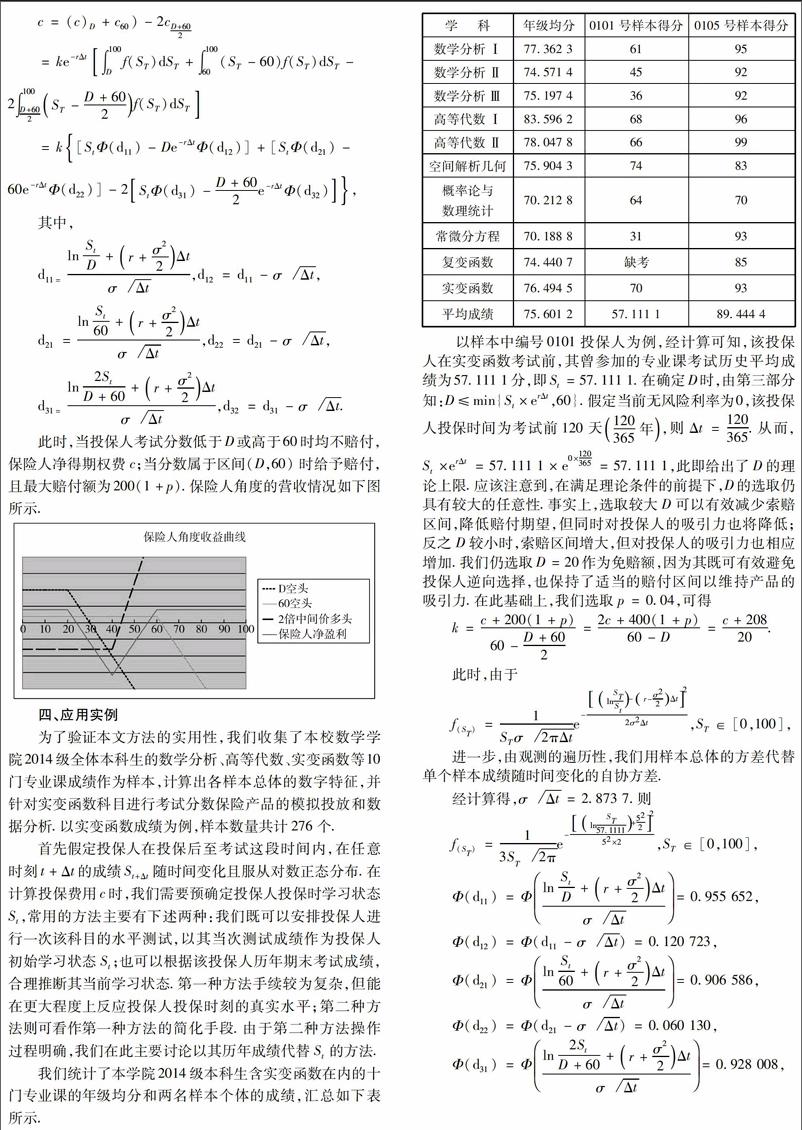
我们统计了本学院2014级本科生含实变函数在内的十门专业课的年级均分和两名样本个体的成绩，汇总如下表所示.endprint