某电站水泵水轮机尾水管进口不同方位点实测压力比较

丁景焕，王 珏，王 君

（1.国网新源控股有限公司技术中心，北京市 100161；2.湖南黑麋峰抽水蓄能有限公司，湖南省长沙市 410213）

0 引言

尾水管进口压力值是水电站设计和运行的重要的调节保证参数之一，尤其是对于抽水蓄能电站，尾水管进口压力保证值能否满足设计要求，关系到机组安装高程的确定及尾水调压井尺寸的确定。对于常规电站，我国规范规定尾水管进口最小压力大于-8m，对于抽水蓄能电站规范中没有明确的规定，设计时一般要求尾水管进口最小压力大于0m，有的甚至要求大于2m。但是，即便对于常规电站，规范中也没有明确-8m是尾水管进口断面压力的平均值还是尾水管进口断面某一点的压力值[1]。

在调试阶段进行甩负荷实验时，一般对尾水管进口断面的一个点或者两个点进行测量，根据测量结果进行过渡过程反演分析，即根据试验工况计算值与实测值的差值对极端工况下的计算结果进行修正，来判断机组能否在全水头范围内安全稳定运行。但是测量结果是包含压力脉动在内的单点的总压力，计算结果是进口断面的均值压力，如果仅以实测的单点的极值压力与计算结果进行对比，差值会比较大。2013年10月，水利水电规划设计总院发布了《水电站输水发电系统调节保证设计专题报告编制暂行规定（试行）》（以下简称《暂行规定》），对于最大水头大于200m的抽水蓄能电站：尾水系统涡流引起的压力下降可按甩前净水头的2%～3.5%选取，计算误差可按尾水管进口压力下降值的7%～10%选取。即便计算结果按照《暂行规定》考虑压力脉动和计算误差后，也会和实测总压力相差较大。因此，压力测点如何选取、测量结果如何合理利用值得探讨。

据此，本文以某抽水蓄能电站为依托，对比分析了尾水管进口不同测点的压力值，提出尾水管进口压力测点的选取方法和实测数据的分析思路，为后续抽水蓄能电站过渡过程反演分析及复核计算提供参考依据。

1 不同方位点尾水管进口压力实测结果分析

某电站装有4台单机容量为300MW的可逆式机组，引水系统为一管双机布置，上游正常蓄水位400m，死水位376.5m，下游正常蓄水位103.7m，死水位65m，水轮机工况额定水头295m，机组转速300r/min，转轮直径D1为5.04m，安装高程15m。

图1 尾水管进口测点位置布置图Fig．1 Measured points of draft tube inlet

在1号流道双机甩100%负荷时（上游水位397.03m，下游水位77.53m），测试单位D采用相同的采样频率对1号机组和2号机组分别在同一高程的不同方位点进行了实测，测点位置A和B如图1所示，分别在尾水锥管段的左上方和右上方，采样频率为300Hz。实测极值结果见表1，1号机组A点与B点实测数据对比见图2、图3，2号机组A点与B点实测数据对比见图4、图5。需说明的是，图2、图4中时间轴-5～0s之间的曲线为机组稳态运行时的实测尾水管压力，图3、图5为局部放大图。

表1 实测数据Tab.1 Measured results at draft tube inlet

图2 1号机组A点与B点实测数据对比Fig．2 Measured results of Unit 1 at points A and B

图3 1号机组A点与B点实测数据对比（局部放大）Fig．3 Measured results of Unit 1 at points A and B（Local magnification）

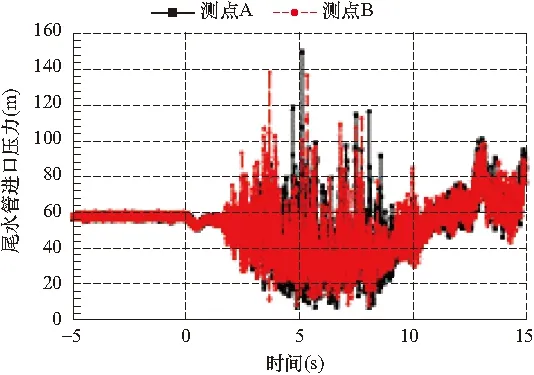
图4 2号机组A点与B点实测数据对比Fig．4 Measured results of Unit3 at points A and B

图5 2号机组A点与B点实测数据对比（局部放大）Fig．5 Measured results of Unit 2 at points A and B（Local magnification）

从表1及图2～图5可以看出，1号机组A、B两个测点虽然在同一高程上，但是压力波动幅度及最小压力值均不相同，B点压力波动幅度远大于A点；2号机组左右两个测点压力波动幅度虽然比较接近，但是尾水管最小压力值也不相同，整体来看，A点的幅度大于B点，A点最小值略小于B点，极值发生时间相差约3s；以上分析说明，同一工况下甩负荷时，同一机组在同一高程上的不同方位测点压力是不完全相同的，这是因为机组在甩负荷过程中，机组高速旋转，尾水管内的流态紊乱，伴随有很大的压力脉动，因此单个测点的极值压力不能代表整个断面的压力，不能仅以实测单点的极值压力与计算结果进行对比，对于实测结果需要进行合理的分析。

2 实测结果与计算结果对比

由于水泵水轮机在甩负荷过程中脉动压力幅值较常规水轮机大很多，但一维数学模型计算所得为均值压力，即水击压力，无法模拟脉动压力[2]，而在机组进行甩负荷试验时，只能对单个点进行测量，由于目前技术水平有限，只能通过对单点实测结果进行合理的分析，再与理论计算值进行对比。

为了便于分析，本节以1s为时间段对尾水管进口压力求移动平均值得到均值压力线，将均值压力线上的最小值与理论计算最小值进行对比，如表2、表3所示。A点、B点的移动平均值与计算值的变化曲线对比见图6、图7。

表2 1号机组实测结果与计算结果对比Tab.2 Comparison between measured results and calculated results of Unit 1

表3 1号机组实测结果与计算结果对比Tab.3 Comparison between measured results and calculated results of Unit 2

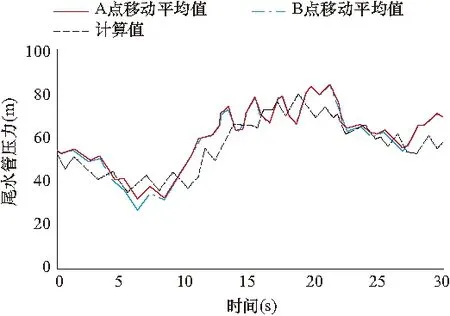
图6 1号机组实测移动平均值与计算值对比Fig．6 Mean measured results at points A and B and calculated results of Unit 1

图7 2号机组实测移动平均值与计算值对比Fig．7 Mean measured results at points A and B and calculated results of Unit 2

从表2及图6、图7可以看出，对A、B两测点取移动平均值后，两测点均值压力线是基本重合的，最小值相差也比较小。取移动平均值之前，1号机组A、B两点的实测最小压力与计算值之差分别为甩负荷前净水头的4.67%、9.37%，2号机组A、B两点的实测最小压力与计算值之差分别为甩负荷前净水头的10.17%、9.4%，均远超过了《暂行规定》要求的修正值的取值范围。取移动平均值之后，1号机组A、B两点的均值压力与计算值之差分别为甩负荷前净水头的0.97%、2.59%，2号机组A、B两点的均值压力与计算值之差分别为甩负荷前净水头的1.64%、1.46%。据此推测，对实测数据取移动平均值后的压力变化可代表整个断面压力变化的趋势。杨桀彬等采用经验模式分解法（EMD）[3]对实测压力的波动信号进行分解，提取均值压力与一维过渡过程计算所得的压力值进行比较，两者的极值结果也比较接近。

需要说明的是，由于本次甩负荷试验工况只对同一断面的两个不同的测点进行了测量，而现在及以前大多数电站在进行甩负荷试验时都是取尾水管进口断面的一个点进行测量，没有更多的工程实例来验证上述观点。建议在今后进行甩负荷实验时可布置3个及以上测点，采用相同的传感器和采样频率进行测量，后续进行甩负荷试验反演分析时，选取科学的方法对试验数据进行分析，如EMD分解法、移动平均法等，确定压力脉动和计算误差更合理的取值范围，为后续电站过渡过程复核计算及尾水管压力保证值的确定提供依据。

3 结束语

本文通过对某抽水蓄能电站双机甩负荷工况同一水力单元的两台机组不同方位测点的尾水管进口压力进行比较，可得出以下结论：由于水泵水轮机固有特性的影响，机组在甩负荷过程中尾水管内流态紊乱，有较大的脉动压力，致使同一机组同一高程尾水管进口断面不同方位测点的实测压力相差较大，因此包含压力脉动在内的单点的极值压力不能代表整个断面的压力，后续进行甩负荷试验反演分析及过渡过程复核计算时，需要对多测点的实测数据进行合理分析，以便更准确的预测电站能否在全水头范围内安全稳定运行。另外，在进行压力测点布置时，可在尾水管进口断面选取3个及以上测点，且传感器尽量靠近测点、引出管尽可能短，以便减小测量误差。

[1] 刘洁颖，杨建东，李进平．尾水管真空度数值计算与模型试验对比研究[J]．人民长江，2005，36（8）：66-68．LIU Jieying，YANG Jiandong，LI Jinping．Comparison and study of the draft tube vacuum between numerical calculation and the model test[J]．Yangtze River．2005，36（8）:66-68．

[2] 杨桀彬，杨建东，王超．基于空间曲面的水泵水轮机机组数学模型及仿真[J]．水力发电学报，2013，32（5）：244-250．YANG Jiebin，YANG Jiandong，WANG Chao．Mathematical model and simulation of pump turbine with characteristic space curves[J]．Journal of Hydroelectric Engineering，2013，32（5）:244-250．

[3] 杨桀彬，杨建东，王超，鮑海艳．水泵水轮机甩负荷过渡过程中脉动压力的模拟[J]．水力发电学报，2014，33（4）：286-294．YANG Jiebin，YANG Jiandong，WANG Chao，BAO Haiyan．Simulation of pressure fluctuation of a pump turbine in load rejection[J]．Journal of Hydroelectric Engineering，2014，33（4）:286-294．