水轮发电机电磁振动及噪声的分析和改造

梁宇强，刘 政，沈 娟，邹应冬

（东方电机有限公司，四川省德阳市 618000）

1 概述

福建G电站为贯流式水电站，装有2台单机容量21MW的灯泡贯流式水轮发电机组，1号机和2号机分别于2007年7月和10月建成投产。两台机投运以后，均存在较严重的振动及噪声问题。通过对原设计气隙中谐波的力波波谱分析，得出定子16，40，64对极反转磁场与转子基波磁场相互作用产生的力波是产生100Hz振动的主要原因；定子376对极反转磁场（一阶齿谐波）与转子352对极磁场（11次谐波），以及定子440对极正转磁场（一阶齿谐波）与转子416对极磁场（13次谐波）相互作用产生的力波是产生600Hz的主要原因，而原设计定子铁芯轭部刚度不足也成为电磁振动超标的诱因之一。根据上述分析结果，我公司通过重新选择槽数、增加铁芯轭部刚度等措施对2台机定子进行了改造，1号机已于2015年3月投入运行。改造后的发电机彻底消除了原有的电磁振动和噪声，定子运行温度也较改造前有所降低，改造效果突出。笔者就该电站的改造思路写成本文，可供存在类似问题的机组的改造处理提供参考。

2 原发电机参数及结构

2.1 发电机主要参数

型 号：SFW21-64/6450

额定容量：23.33MVA

额定功率：21MW

额定电压：10500V

额定功率因数：0.9

额定励磁电压：212V

额定励磁电流：800A

额定频率：50Hz

定子铁芯内径：φ6000mm

定子铁芯外径：φ6450mm

定子铁芯长度：1200mm

定子槽数：408

每极每相槽数：8+1/2

2.2 定子原有的结构形式

定子采用贴壁结构，铁芯无径向风沟。铁芯外径与机座壁之间采用涂铝填充传热。铁芯全圆由34张12槽片叠成整圆，槽形尺寸16.6×126.6mm，铁芯轭部（94mm）与齿部（126.6mm）比值为0.74。每张冲片采用4-M16穿芯螺杆把紧（见图1）。冲片齿部开有通风沟槽，用于轴向通风冷却定子铁芯（见图2），同时压指上也开了通风沟槽（见图3）。

3 存在的问题

G电站机组投运后出现了较大的噪声和振动。人站在封水盖板上能够明显听到机组发出“嗡嗡”的高频声响，而且有脚麻的感觉，其中1号机噪声明显比2号机要大。

图1 改造前定子铁芯的穿芯螺杆结构Fig．1 Screw core structure of stator core before transformation

图2 改造前定子铁芯冲片Fig．3 Before the transformation of the stator iron core punching

图3 改造前铁芯端部压板及压指Fig．3 Before the transformation of the iron core of the end plate and pressure finger

经对1号机噪声测试表明，噪声中心频率为630Hz，并随着运行负荷增加而逐步增大，其现场测量值均在100dB以上，远超过国家混频标准85dB，比同类型大10～20dB以上，其中1号机灯泡头入口处测量得中心频率为100Hz的噪声达119.8dB。

振动测试结果表明，带负荷工况下，机座径向振动的主要频率为100Hz与600Hz。其中100Hz振动在灯泡头处其振动加速度测量值为0.954m/s2，是同类型电站机组测量值0.11m/s2的8～9倍；600Hz振动加速度测量值2.29m/s2，是同类机型（福建D电站为0.328m/s2）的 6～7 倍。

4 定子铁芯电磁振动分析

4.1 基本原理

电动机运行时，定、转子电流产生磁势并在气隙中建立磁场，空载运行时只有励磁磁势建立磁场。当磁场交变时便产生作用于定子铁芯的径向力波，引起电磁振动。由电机学理论，气隙磁场磁密分布是关于空间和时间的函数，可表示为：

式中Bv——谐波幅值，

v——谐波的极对数，

fv——该次谐波经过定子的频率，

θ——空间机械角度。

根据麦克斯韦方程，气隙磁场的谐波分量相互作用是产生径向电磁力：

由式（1）和式（2）可知，电磁力波分量也是关于空间和时间的函数，在计算电磁振动时主要考虑节点对数不为零的力波分量。电磁力波根据产生原因分为三类：

①由单个磁场单独作用产生，电磁力波的激振频率为2fv，节点对数为2v；

②由相同转向两个磁场相互作用产生，其中一个分量的激振频率为fv1-fv2，对应的节点对数v1-v2，另一分量的激振频率为fv1+fv2，对应的节点对数为v1+v2；

③由相反转向两个磁场相互作用产生，其中一个分量的激振频率为fv1-fv2，对应的节点对数v1+v2，另一分量的激振频率为fv1+fv2，对应的节点对数为v1-v2。

4.2 力波波谱分析

电磁噪声本质上是由电磁振动引起的。在分析电磁振动之前，首先对磁场中的力波进行分析。

对于q=b+c/d的三相分数槽绕组，其中电枢反应磁场谐波极对数为v1=（6k1/d+1）P，（k1=0，±1，±2，...），其中负号表示反转磁场；对于转子磁场，由于磁极的对称性，其磁场只存在奇次谐波，其谐波极对数为v2=（2k2+1）P，（k2=0，1，2，...）。

根据4.1的基本原理，当极对数为v1，v2两个磁场相互作用时，产生的力波的节点对数及力波频率见表1。

表1 不同极对数谐波对应的力波特性Tab.1 The characteristics of the force wave corresponding to different pole logarithmic harmonics

力波节点对数M越小，引起铁芯振幅越大。因此主要对力波节点对数M较小的力波进行分析，得到主要力波波谱见表2。表2中，在定子端，由于定子基波电流频率为50Hz，因此由绕组空间分布引起的空间磁势谐波频率恒为50Hz；在转子端，由于磁势谐波随着转子同步旋转，因此转子谐波频率正比于谐波极对数（即 50Hz，150Hz，250Hz，350Hz...）。

从力波波谱可以看出

（1）100Hz振动主要由定子v1=16，40，64对极反转磁场与转子基波磁场相互作用产生。

（2）600Hz振动主要由定子v1=376对极反转磁场（一阶齿谐波）与转子v2=352对极磁场（11次谐波），以及v1=440对极正转磁场（一阶齿谐波）与转子v2=416对极磁场（13次谐波）相互作用产生。

4.3 100Hz电磁振动分析

电磁力波引起的铁心振动，其振动幅值为

式中Pn—— 谐波磁场与气隙主磁场叠加，在气隙单位面积上产生的径向力，kg；

M——力波节点对数；

f0——该力波振型的固有频率，Hz；

f——电磁激振频率，Hz；

E1——定子铁心弹性模量。

其中固有频率f0可按式（4）计算

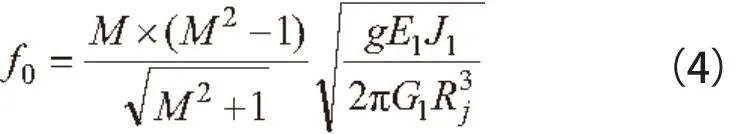
式中J1——铁芯轭部断面惯性矩，cm4；

G1——定子线圈及铁芯总重量，kg；

Rj——定子磁轭的平均半径，cm。

从上式可以看出，径向力Pn越大，力波节点对数M越小，则振动幅值就越大，因此对于100Hz电磁振动，定子绕组谐波主要考虑转向反转，且与转子基波磁场相互作用产生的力波节点对数最少的部分，对照表1的力波波谱可知，主要考虑的谐波为极对数P取16、40、64。

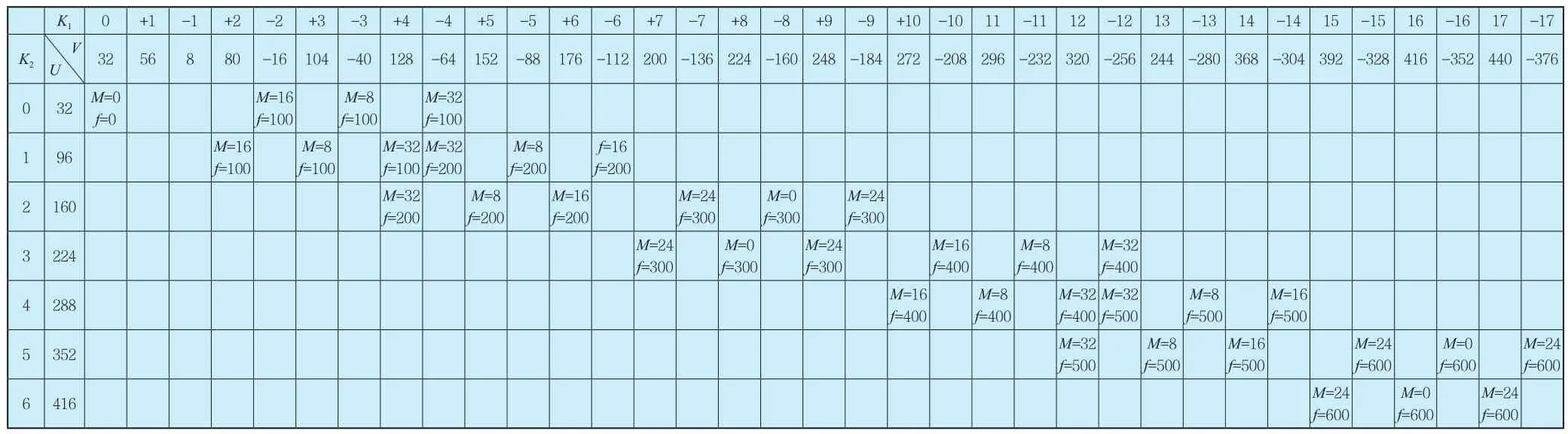
表2 改造前负载时定转子磁场产生的力波波谱Tab.2 Force wave spectrum produced by magnetic field of stator and rotor in front of load

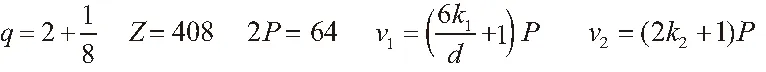
在计算时，定子铁芯弹性模量E1的选择是个重要的问题，它与许多因素有关。根据以往机组振动实测值推断，通常取E1=1.1×106kg/cm2是比较合适的。为了能够比较全面了解该电站的铁芯振动情况，这里 分 别 取E1=1.3×106kg/cm2，E1=0.9×106kg/cm2，E1=0.9×106kg/cm2进行计算、比较。

另外，发电机定子铁芯振动需分别考虑冷态和热态两种工况。冷态时认为铁芯不受机座影响而单独振动；热态时，铁芯和机座合为一个自由圆环振动。相关计算方法可参考文献[1]，本文不再赘述。

根据G电站提供的原定子结构参数，计算出铁芯100Hz振动见表3～表5。

表3 电磁振动计算结果（1）Tab.3 Calculation Results of Electromagnetic Vibration（No.1）

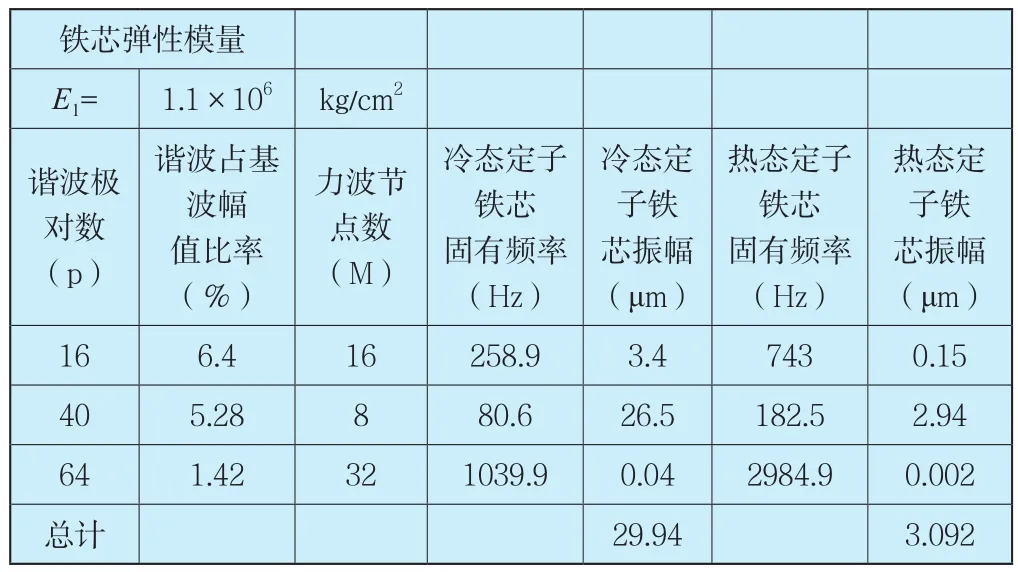
表4 电磁振动计算结果（2）Tab.4 Calculation Results of Electromagnetic Vibration（No.2）

从上面计算结果可知，铁芯冷态时，当E1=1.3×106kg/cm2100Hz径向振动幅值超过国标允许的30μm，8节点力波对应的铁芯固有频率87Hz，比较接近100Hz激振力频率，很容易引起铁芯共振。

表5 电磁振动计算结果（3）Tab.5 Calculation Results of Electromagnetic Vibration（No.3）

4.4 600Hz电磁振动分析

根据表1的波谱分析，引起600Hz振动的，主要是定子328极以及376极谐波与转子352极（11次谐波）相互作用产生的。其中定子376对极谐波为一阶齿谐波，其绕组系数与基波相同，与转子11次谐波之间相互作用力也最大，因此，600Hz振动主要考虑定子一阶齿谐波与转子11次谐波作用结果。

通过表1波谱分析可知，600Hz振动力波节点对数为24对。根据电站提供的定子结构参数计算该力波对应的铁芯固有频率发现：M=24时定子铁心计算固有频率约为634Hz（E1=1.1×106kg/cm2），与齿谐波引起的高频磁力激振频率600Hz比较接近，作用于定子铁芯时径向振幅较大。

4.5 电磁振动分析结论

通过以上分析，可以看出100Hz电磁振动的振幅超过国标允许值，且8节点力波对应的铁芯固有频率87Hz，接近激振力频率100Hz，而600Hz振动力波对应的铁芯固有频率也接近激振力频率，这都会引起铁芯共振。

为了减少600Hz振动，可以改变定子铁芯的固有频率，使得该振型的固有频率远离幅值较大的电磁力的激振频率600Hz。

为了减少100Hz振动，可以通过削弱次谐波幅值，或者增大力波节点对数来减少振幅。前者可以通过改定子绕组接线，增大正负相带不对称度，从而谐波减少绕组系数的方式解决；后者可以通过重新选槽，改变谐波极对数解决。由于贯流机尤其是贴壁式贯流机，引线端的空间非常狭小，通过改接线的方式实现比较困难，另外考虑到原厂家定子结构设计存在一些设计缺陷，因此选择了整个定子重新设计的改造方式。

5 改造措施

改造措施主要有以下几个：

（1）重新选择定子槽数。定子槽数由改造前的408槽更改为432槽。定子槽数的选择主要考虑了几个因素：首先，新槽数的选择必须使次谐波引起的100Hz振动大幅度降低，而且低节点力波对应的定子铁芯固有频率远离100Hz（一般认为不在80～130Hz这个范围内是安全的）；其次，定子一阶齿谐波分量与转子高次谐波作用引起的力波所对应的铁芯固有频率远离激振力频率。

（2）增加定子铁芯轭齿比。原有铁芯轭齿比偏小，只有0.74，从而使得齿部不能得到有效的压紧，在交变电磁力作用下，齿部振动会加剧。长此以往，齿部冲片有可能会割破线棒主绝缘，造成绕组接地故障，同时齿部由于反复振动产生机械疲劳而断裂。改造后轭齿比提高到0.864。

（3）改善铁芯压紧方式。定子铁芯采用穿心螺杆+碟形弹簧的压紧方式，保证铁芯长期压紧，补偿铁芯漆膜收缩，保证定子铁芯长期运行而不松动；铁芯两端部黏结，加强铁芯的整体性，从而加强铁芯端部刚度，减小铁芯振动。改造后铁芯端部固定方式如图4所示。

（4）降低热负荷。改造后槽数增加，齿距变小，齿部不宜开轴向通风沟。因此只能通过增加定子用铜量，大幅降低定子的电流密度，从而有效减低机组热负荷。

图4 改造后铁芯端部固定方式Fig．4 After the iron core end fixing method

（5）降低线棒温度。定子线棒材料采用了达到国际先进水平的双玻璃丝包线，为单匝杆式波绕组，并采用小于360°的换位方式；线棒拟采用VPI绝缘系统，主绝缘比多胶模压系统减薄，这样使得槽内绝缘传热系数提高，将热量传递给铁芯，以达到降低线棒温度的目的。

6 改造效果

6.1 改造后力波波谱分析

每极每相槽数q由改造前的2+1/8变成改造后的2+1/4，由于分母减少，因此分数次谐波也大为减少。按照前文介绍的理论，改造后的力波波谱见表6。

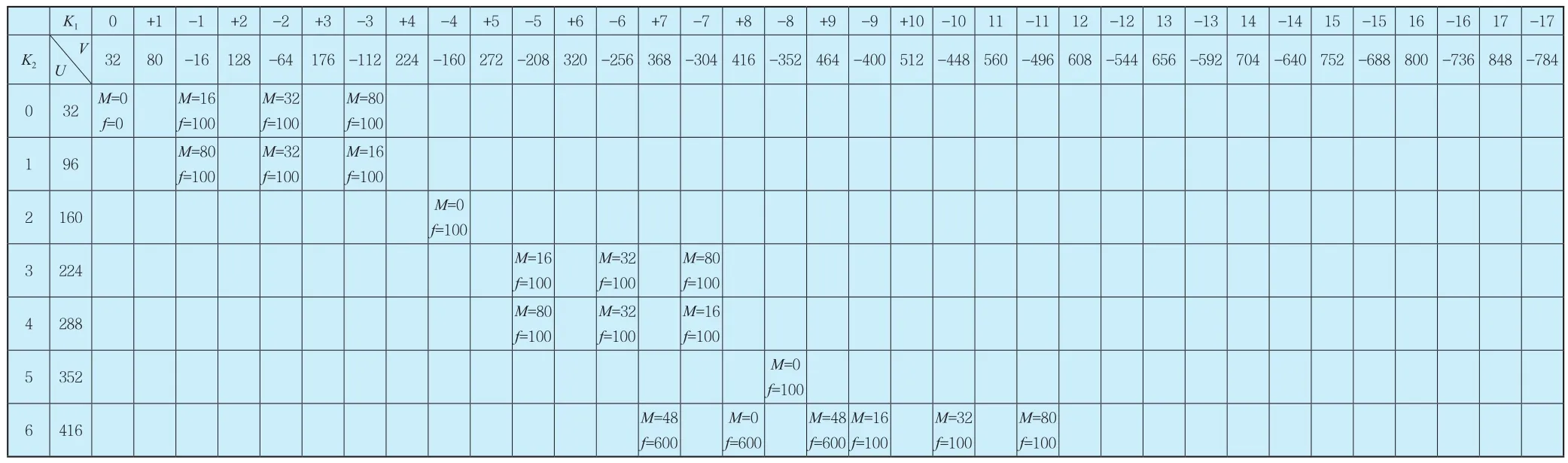
表6 改造后负载时定转子磁场产生的力波波谱Tab.6 The spectrum of force wave generated by the fixed rotor magnetic field after the transformation

从上表的力波波谱可以看出，改造后，占100Hz电磁振动比重最大的8节点分量消失了，力波最低节点对数由8对提高到了16对；600Hz电磁振动的力波节点数由改造前的24对节点提高到48对节点。根据前文的改造思路，下面将分别计算100Hz电磁振动幅值，以及600Hz振动力波对应的定子铁芯固有频率，以验证改造效果。

6.2 改造后100Hz电磁振动分析

根据表6可知，100Hz电磁振动主要由定子16，64，112对极反转谐波与转子基波相互作用产生。相应的电磁振动计算结果见表7～表9。从计算结果可以看出，改造以后的铁芯100Hz电磁振动幅值远远小于国标规定的30μm，达到优良水平。

6.3 改造后600Hz电磁振动分析

对于600Hz电磁振动，改造前主要由于激振力波对应的铁芯固有频率与激振力波频率比较接近引起。改造后，从表6可知，600Hz电磁振动主要是由定子368对极以及464对极正转谐波（1阶齿谐波）与转子416对极谐波相互作用产生的。利用式（4）计算这两种力波对应的铁芯固有频率见表10。

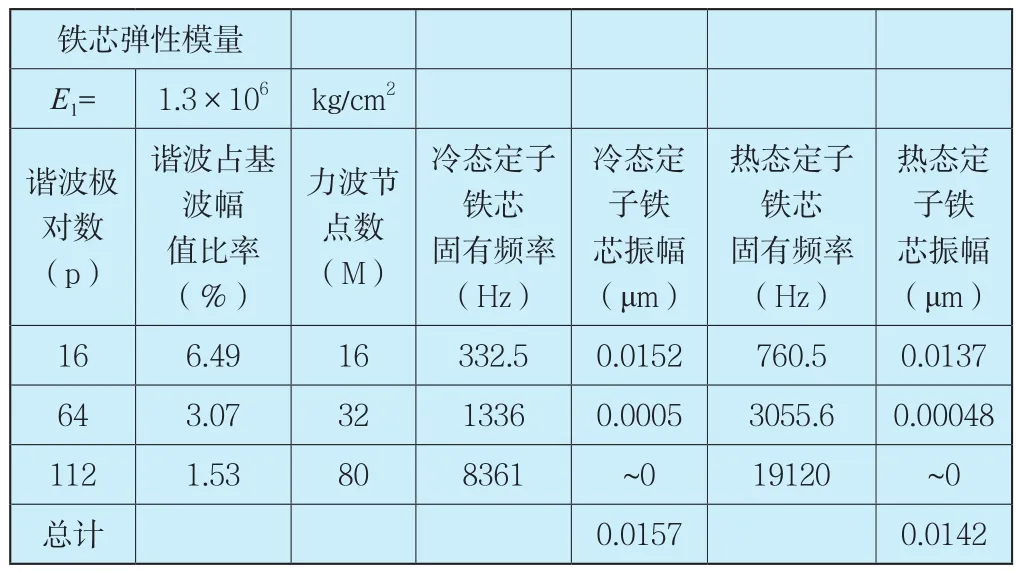
表7 电磁振动计算结果（4）Tab.7 Calculation Results of Electromagnetic Vibration（No.4）

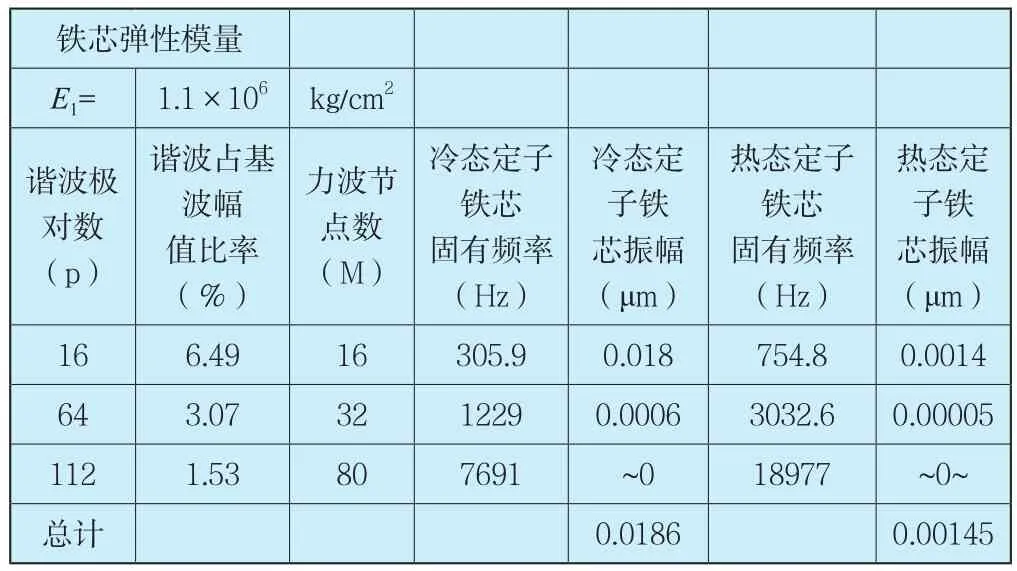
表8 电磁振动计算结果（5）Tab.8 Calculation Results of Electromagnetic Vibration（No.5）

表9 电磁振动计算结果（6）Tab.9 Calculation Results of Electromagnetic Vibration（No.6）

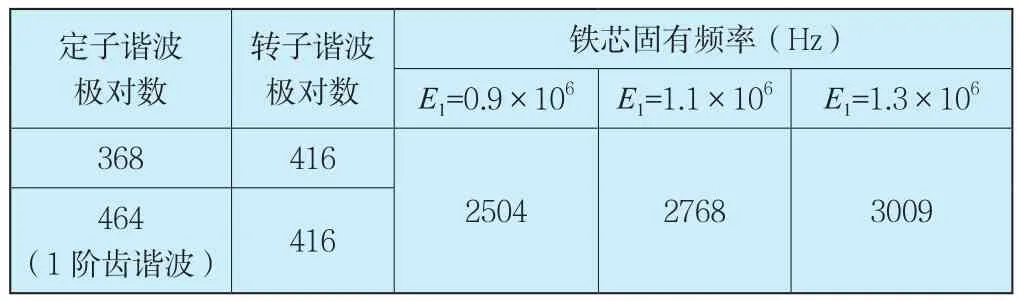
表10 改造后600Hz激振力波对应的铁芯固有频率

从计算结果可以看出，600Hz激振力波对应的铁芯固有频率远远高于600Hz，完全消除了改造前铁芯存在600Hz共振的情况。

6.4 改造后铁芯电磁振动电站实测值

1号机于2015年 3月7日下午并入系统运行，并按保护、励磁改造要求缓慢上升机组负荷运行，机组在升负荷运行过程中，机组整体振动声音及发电机电磁声均正常。具体情况如下。

（1）“嗡嗡嗡”的电磁噪声人耳已听不到，与1号机改造前及未实施改造的2号机组运行声音形成巨大反差。

（2）1号机流道盖板处强烈麻脚感消失。

（3）噪声测试情况：满负荷工况下灯泡头入口处上方1 m在改造前测得混频噪声为102.4dB，改造后测得混频噪声值为92.2dB。

（4）机组温度与同工况2号机及改造前同工况1号机对照见表12，环境温度12℃。从表11中可以看出，在相同工况下，1号机改造后定子线圈温升、铁芯温升均明显降低。

表11 1号机改造前后、2号机改造前温升对比表

7 结束语

振动和噪声是衡量发电机运行性能的重要指标。对于电磁振动，一般只能通过改定子绕组接线，减少绕组系数来减少谐波幅值，但是绕组端部引线结构复杂；或者重新选择槽数，减少分数次谐波的次数。针对G电站定子引线端空间小，且原设计铁芯轭部偏小的特点，选择了重新选择槽数的改造方案。另外还采用了增加铁芯压紧、减少线圈、铁芯的多项改造措施。由于改造方案采用的措施得当，改造后机组的振动噪音大幅度减少，取得了令人满意的效果。本文的分析和改造思路可为今后处理类似问题提供参考。

[1] 白延年．水轮发电机设计与计算．北京：机械工业出版社，1982．BAI Yannian．Design and calculation of hydro generator．Beijing:Mechanical Industry Press，1982．

[2] 许实章．交流电机的绕组理论．北京：机械工业出版社，1985．XU Shizhang．Windings theory of AC motor．Beijing: Machinery Industry Press，1985．

[3] 赵贵前．大型抽水蓄能机组定子绕组固定技术与状态评价的分析 [J]．水电与抽水蓄能，2015，1（1）：21-27．Zhao Guiqian．Analysis of stator winding fixation techniques and its condition evaluation for large pump-storage units[J]．Hydropower and Pumped Storage，2015，1（1）：21-27．

[4] 陈泓宇，汪志强，李华，程振宇．清远抽水蓄能电站三台机组同时甩负荷试验关键技术研究[J]．水电与抽水蓄能，2016，2（5）：28-39．CHEN Hongyu，WANG Zhiqiang，LI Hua，CHENG Zhenyu．Review of the load rejection test of the pumped storage 3 units together in Qingyuan pumped storage power station[J]．Hydropower and Pumped Storage，2016，2（5）：28-39．

[5] 付朝霞．大型抽水蓄能机组发电电动机定子局部放电的研究[J]．水电与抽水蓄能，2016，2（3）：4-12．FU Zhaoxia．Studies of partial discharge for generator-motor stator in large pumped storage unit[J]．Hydropower and Pumped Storage，2016，2（3）：4-12．