导叶关闭速度对尾水管流场影响的数值模拟

霍天浪，王 倩

（中国电建集团西北勘测设计研究院有限公司，陕西 西安，710065）

水轮机日常运行过程中，常需进行工况的转换。水轮机工况的转换通常是通过调节活动导叶的开度来完成的。不当的活动导叶关闭速度对尾水管的安全造成很大的危害。研究活动导叶关闭速度对尾水管的影响迫在眉睫。

在过去的几十年中，对于水轮机工况转换中导叶关闭的相关研究大部分都是集中在通过调节保证计算和分析[1]，或者是通过对水轮机实际运行来进行检测[2]，这些计算方法都不能很好的对导叶的实际关闭过程很好的模拟。近些年，计算机技术和数值模拟方法都有了很好的发展，对动网格技术的研究越来越多[3-4]，许多学者采用动网格技术来对边界运动的过程进行数值模拟[5-6]，这验证了可以采用动网格技术来对导叶关闭过程进行瞬态数值模拟。

本文采用动网格技术，对A855-37.4模型转轮在五种不同关闭速度下的导叶关闭过程进行了三维瞬态数值模拟，分析不同关闭速度对尾水管内的动态特性以及内部流场的影响。

1 计算模型

本文计算所采用的模型如图1（a）所示，由于计算机水平的限制，故采用单流道导叶，转轮为全流道。水轮机参数为：活动导叶数z=24，转轮叶片数z=15，转轮直径D1=0.374 m，活动导叶额定开度a=33°。模型活动导叶区域采用四面体网格，转轮和尾水管采用六面体网格。在尾水管内布置六个监测点，监测点位置示意图如图1（b）所示，b1和b2位于距转轮出口0.3倍的转轮直径处，c1和c2位于锥管段末端，d1和d2位于锥管段中间位置。

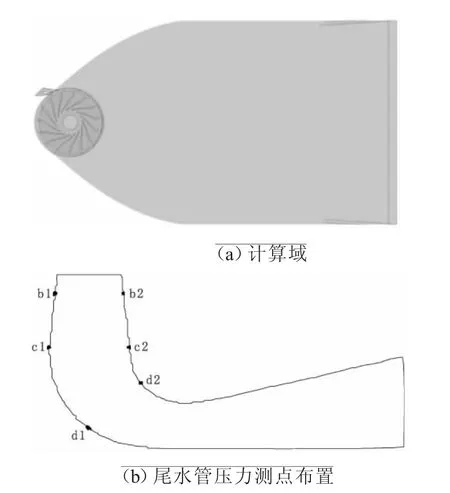
图1 计算几何模型及尾水管压力测点布置示意图

2 数值计算方法

2.1 基本控制方程

在活动导叶附近的水流流动属于复杂的三维非定常不可压缩流动，基本控制方程为Reynolds时均方程，由湍流脉动所造成的量加下标t，省略各变量的时间平均标志“—”，湍流模型选用RNG两方程模型，具体方程如下[7]：

连续方程：

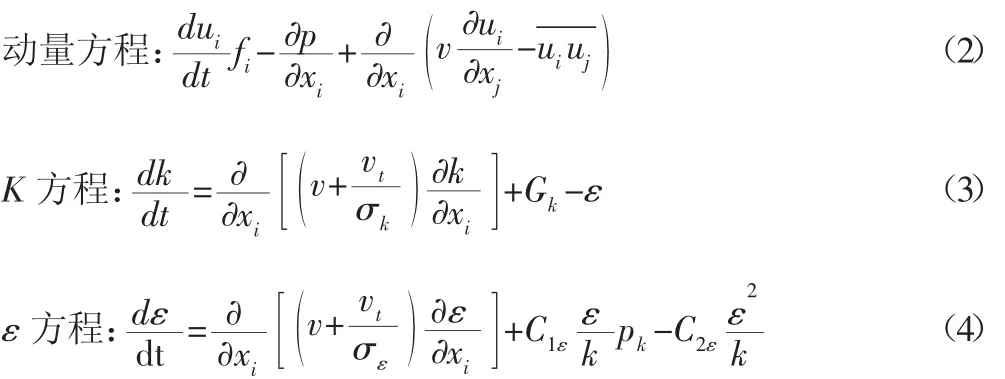
式中：t为时间；ui和xi分别为速度分量和坐标分量；v为运动粘性系数；p 为修正压力；fi为质量力；vt=cμk2/ε 为湍流粘性系数；

其中 δk，δε，C1ε，C2ε，cμ，为经验系数，δk=1.0，δε=1.3，C1ε=1.44，C2ε=1.92，cμ=0.09；Gk为平均速度梯度引起的紊动能产生项，Gk=vt为雷诺应力项，用RNG k-ε两方程模型来封闭。

2.2 边界条件

进口边界条件采用质量流量，不同导叶开度对应的质量流量见表1。导叶开度与质量流量关系特性曲线如图2（a）所示。

表1 不同导叶开度下质量流量特性曲线

图2 导叶开度与质量流量及时间的特性曲线图

质量流量随导叶开度的变化规律通过Profile文件编译到Fluent软件中，随着导叶开度的变化流量相应的变化。出口边界条件为自由出流。固体边界为无滑移边界条件，采用标准壁面函数来处理壁面边界。活动导叶采用直线关闭规律关闭，用FLUENT软件提供的UDF（用户自定义函数）来控制活动导叶的关闭规律。计算中时间步长设为0.01 s，在计算过程中，每一步计算的收敛残差设置为10-3。活动导叶的开度变化为从额定开度（a=33°）关闭到小流量开度（a=9°），关闭时间分为五种 6 s、9 s、12 s、18 s和 24 s。导叶关闭规律示意图如图 2（b）所示。

为得到更加准确的模拟结果，本文在计算过程中使用定常计算的收敛结果作为非定常计算的初场来进行动网格非定常的计算。

3 结果分析

3.1 流态分析

图3（a）-（e）为不同导叶关闭规律下不同开度时尾水管子午面上的流线分布图。从两方面来进行分析：

首先，对同一种关闭规律不同导叶开度时尾水管子午面上的流线分布进行分析。导叶关闭时间为6 s时，由图3（a）可以看出：开度为32°时，尾水管流线分布良好，流线顺畅，未出现回流现象；随着开度减小，开度为26°时，弯肘段出现回流，但大部分流线顺畅；开度为23°时，回流流线增多，回流范围增大，只在弯肘段中出现；随着导叶继续关闭，开度为13°时，导叶基本关闭完成，水流已不能顺畅流入下游，直锥段和弯肘段均出现回流；开度为9°时，导叶关闭完成，机组处于小流量工况下，子午面上的流线紊乱，尾水管直锥段、弯肘段和水平扩散段的前段均出现回流，水流不能顺畅流入下游。可知同一种关闭规律下，导叶开度越小，对尾水管的稳定影响越大。

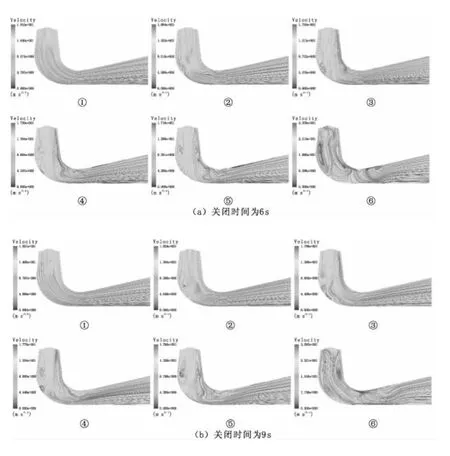
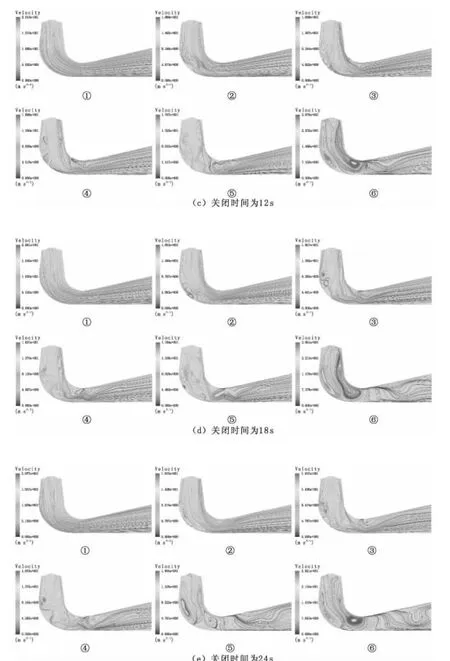
图3 不同导叶关闭速度下尾水管子午面上流线分布

表3 额定工况下定常计算尾水管内监测点计算结果

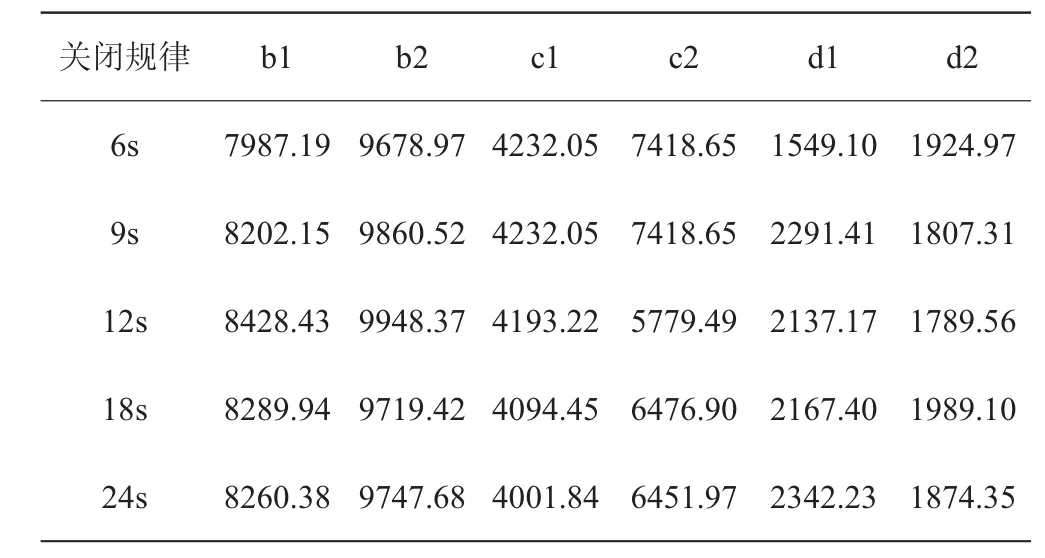
表4 导叶关闭过程中尾水管监测点上压力最大上升值

其次，对同一导叶开度不同导叶关闭规律下尾水管子午面上流线分布进行分析。由图3（a~e）可以看出，开度为32°时，关闭速度对尾水管内流线分布影响不大，水流能顺畅流入下游；开度为23°时，关闭速度越慢，子午面上流线分布越紊乱；开度为9°时，导叶基本关闭完成，关闭时间为6s时（图3（a）⑥），只在水平扩散段前段出现回流，然后流线趋于平滑，关闭时间为24s时（图3（e）⑥），尾水管的直锥段、弯肘段和水平扩散段都出现了回流。可知同一开度下，关闭速度越慢，对尾水管的稳定影响越大。

3.2 监测点压力最大上升值

对额定工况下尾水管内流场进行定常计算，获得在导叶关闭过程中，不同关闭速度下的监测点上压力最大上升值。

由表4可以看出，在同一种关闭速度下，尾水管中压力最大上升值从进口到出口依次减小，靠近进口处的监测点b上的压力上升值最大，靠近出口处的监测点d上的压力上升值最小。不同关闭速度下，监测点上压力最大上升值没有明显规律。

4 结论

本文以某一混流式水轮机为研究对象，采用Fluent软件中的动网格技术模拟了导叶关闭过程中不同关闭速度下尾水管内部的非定常流动，对比分析了尾水管中流线及监测点最大压力上升值。得出以下结论：

（1）在导叶关闭过程中，随着开度的减小，尾水管中水流流态越差，水轮机在小开度工况下运行对尾水管的损害较大。

（2）导叶关闭速度对尾水管内流场有较大的影响，在导叶关闭较小开度时，关闭速度对尾水管内流场影响不大。随着导叶开度的减小，导叶关闭速度越慢，尾水管中的水流流态越紊乱，对尾水管的危害越大。

（3）同一种关闭速度下，尾水管内压力最大上升值从进口到出口依次降低，在靠近尾水管进口处的压力变化范围最大。

[1]杨建东.导叶关闭规律的优化及对水力过渡过程的影响[J].水力发电学报，1999（02）.

[2]丁万钦,唐拥军.三峡右岸电站26F机组过速过程异常振动分析[J].水电与新能源.2013（01）.

[3]张军,耿继辉,谭俊杰.三维非结构运动网格的生成[J].弹道学报,2004(01).

[4]史忠军,徐敏,陈士橹.动网格生成技术[J].空军工程大学学报(自然科学版),2003(01).

[5]黄剑锋，张立翔，王文全，等.基于动网格的活动导叶流道内湍流场数值模拟[J].排灌机械工程学报,2010,28(02)：140-143.

[6]华晔.基于动网格技术的水轮机瞬态流动分析[D].西安理工大学，2010.

[7]隋洪涛，李鹏飞.动网格工程仿真与案例实战[M].北京：人民邮电出版社，2013，15-16.