水电站和电力调度量测系统的状态估计探析

2018-01-15刘小龙

陕西水利 2017年6期

关键词：权函数等价权值

刘小龙，刘俊

（1.陕西省汉中市石门水库管理局，陕西汉中 723000；2.中国电力科学研究院，江苏南京 210003）

0 引言

水电站和电力调度系统量测数据在采集、传递、交换过程中不可避免存在误差，包括个别可预测的偶然误差和带有部分规律性的系统误差。此外还包括偏离实际量测数据变化轨迹较远的数据，即粗差。粗差的出现约占量测系统量测总数的1%~10%[1]。

随着新理论在电力系统中的应用，多种抵御粗差能力的状态估计新方法应运而生。如新息图状态估计[2]、最小信息损失状态估计[3]等，这些方法分别从不同思路获取有利于估计的信息，提高了状态估计抵御粗差的能力。

本文提出了一种基于线性分段权函数的选权迭代状态估计方法，并在调度仿真平台上验证，该方法通过选取“三段式”线性权因子函数，根据量测残差确定不同设备类型量测点等价权值，将传统加权最小二乘状态估计方法[4]和抗差估计理论相互结合，既保留加权最小二乘估计计算的高效快速性，又使得状态估计算法本身具备较强抵御粗差的能力。

1 传统粗差检测和定位

状态估计传统的粗差检测和定位一般采用估计-粗差检测与辨识-再估计-再粗差检测与辨识的两轮迭代计算模式，即估计后辨识的方法。对于较大偏差的量测粗差数据可以将其识别出来，但对于偏离真值较小的量测数据，则无法通过粗差检测和定位完全将其影响消除，导致这些不正确的数据参与了状态估计，从而对正确数据形成污染，造成误检和漏检。

针对上述问题，本文提出了基于线性分段权函数的选权迭代状态估计方法，对于超过辨识门槛的量测数据但仍可用于计算的量测量，即对估计精度提高有贡献的量测量，不采用删除和抑制的策略，而采取降权方法降低该量测的权重，使该量测通过降权方法仍参与状态估计计算，为状态估计精度提高作出贡献。而对于残差很大的不良数据，权值强制为零，使其不影响状态估计计算精度。

2 选权迭代状态估计方法

选权迭代状态估计方法是在粗差不可避免的情况下，选择适当的算法使电网状态量估计尽可能减免粗差的影响，得出正常模式下的最佳估值。其原则是充分利用有效量测，限制利用可使用量测，排除有害量测。

权函数是衡量选权迭代状态估计方法优劣的一个重要因素，经典选权迭代状态估计的权函数都是以降权思路提出的，通过不断迭代，使含粗差项量测值的权趋近少零，本文也是基于上述思想，通过建立分段线性的权因子函数，得到既有较强抵御粗差能力，又有较高效率的估值。

2.1 问题求解

选权迭代状态估计通过等价权函数将抗差估计理论与最小二乘形式相互结合，其权是残差的函数，计算迭代式为：

本文所述求解方法与传统的最小二乘算法的区别是：本文方法在估计迭代计算中量测权值随量测残差变化，其权值按照三段式线性权函数确定。而最小二乘算法在求解过程中权值保持不变；本文方法对可利用量测采取线性函数降权处理模式，而传统状态估计粗差检测和定位方法中对量测采用“非此即彼”一刀切处理模式。

2.2“三段式”权函数

选权迭代状态估计根据量测残差所处区域，将权区域划分为保权区、降权区、淘汰区。从而充分利用有效信息，限制性利用可用信息，排除有害信息，因此将这种估计方法使用的权函数称为“三段式”权函数，其函数曲线如图1所示。

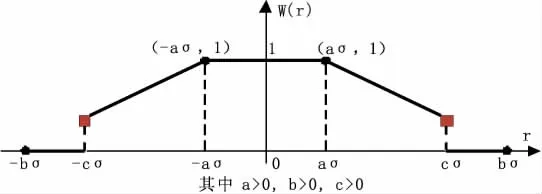
图1“三段式”权函数

图1中a、b、c均大于零，其值，其中a为保权区边界系数，b为降权斜率控制系数，c为淘汰区边界系数，为量测误差的标准差，它决定于量测、变换与传送各个环节误差的总和，其值由缺省量测权值确定，r为测点量测残差，w（r）为测点权因子。

根据测量误差理论，边界系数a可取2.5，这个区间以外的量测值既必能完全排除又要限制其有害影响。当残差超出±10σ时，在量测值分布模式可用的情况下，这部分数据不应作为有用的量测信息，即取权值为0。本文算例中a取2.5，b取11.5，c取10.6。

由图1可知，当残差r绝对值在aσ以内时，权因子w取1，即为其保权区；当残差 r绝对值处于[aσ，cσ]区间时，权因子取为线性函数形式，权因子w逐渐减小，降低量测值在计算中的权重，量测数据偏差较大时，对其分配的权值也就越低。而当残差r绝对值处于（cσ，+∞）区间时，这些数据不应作为量测信息，即取w等于0，为淘汰区。从函数的正半轴看过去，函数分三段，分别对应着量测数据的有用数据，有效数据以及有害信息。即相应的保权区、降权区、淘汰区，其权因子分别为：

当-aσ≤r≤aσ 时，保权区权因子

当 aσ＜r≤cσ 时，降权区权因子函数

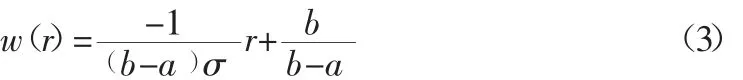
当-cσ≤r＜-aσ 时，降权区权因子函数

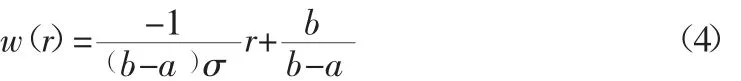
当 r＞cσ 或 r＜-cσ 时，淘汰区权因子

2.3 量测等价权

通过“三段式”权函数计算量测权因子，量测等价权为：

当-aσ≤r≤aσ 时，保权区量测等价权P¯为

当 aσ＜r≤cσ 或-cσ≤r＜-aσ 时，降权区量测等价权为

当 r＞cσ 或 r＜-aσ 时，淘汰区量测等价权为

式(6)和式(7)中，w'为量测点的初始缺省权值。根据各量测残差求出对应的权因子后，通过式（6）~式（8）计算量测等价权，利用该等价权通过加权最小二乘迭代方法进行求解。

3 计算流程

基于线性分段权函数的选权迭代状态估计在实现上采用传统PQ解耦最小二乘估计的求解迭代方法，相比加权最小二乘法方法不同在于其量测权值随量测残差而变化。其残差是指在每次迭代终了时量测量与该次迭代结果所得的量测估计量之差，残差绝对值大的量测的权值会被减小，从而在下一次迭代中的影响也随之减小，如此迭代下去直到收敛为止。因此，仅需对传统加权最小二乘估计软件作很少的修改就能达到自抵御粗差的能力，相应的计算流程如图2所示。计算主要步骤如下：

步骤1：置迭代计数器为1，采用平启动方式计算有功支路和注入潮流、有功残差，进行第一次有功迭代，判断有功最大偏差是否小于设定门槛，设置选权迭代标志。

步骤2：根据式(2)～式(5)计算测点等价权因子，在此基础上计算量测等价权值，重新形成有功量测雅克比矩阵以及有功因子表分解。

步骤3：根据有功最大偏差量判断有功是否收敛，否则进行无功迭代，其过程与有功迭代相似，当有功、无功偏差均小于收敛精度时状态估计迭代计算完成。

图2 选权迭代状态估计计算流程

4 算例分析

为验证基于分段线性权函数的选权迭代状态估计的计算性能，本文在智能电网调度试验验证平台上选用某地调实际数据进行实验验证。其建模厂站数397个，建模线路总数1317个，建模变压器总数733个，建模机组95台，建模负荷总数6497个。电网计算母线数为1558条，量测总数为8771个。

本文将从粗差检测和定位门槛对状态估计计算精度影响和算法抵御粗差性能指标两个方面对所提算法进行验证。

4.1 状态估计结果指标

状态估计精度反映状态估计结果与其真值之间的靠近程度。对基于标准节点的系统，由于标准节点的电力系统状态真值（取潮流值）是已知的，这时选择状态估计结果和状态真值之间的偏差作为估计精度的量化指标。但实际电力系统的状态量真值是未知的，量测的估计误差也不可知，因此不能再采用基于真值的量化指标，本文所定义的状态估计性能指标如下：

1）状态估计精度指标G(s)

G(s)指标如式（9）所示。其中 s为门槛值；Dot|r|＜s为量测估计残差绝对值小于门槛值s的量测点数；Dottotal为量测总点数。

2）状态估计有功目标函数值T11

T11指标如式（10）所示。其中zip为有功量测值；wip为有功量测权重；rip为有功量测残差。

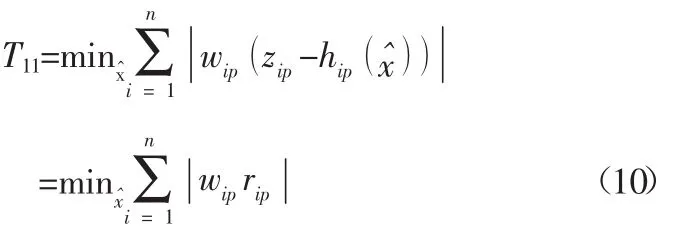
3）状态估计无功目标函数值T12

T12指标如式(11)所示。其中ziq为无功量测值；wiq为无功量测权重；riq为无功量测残差；

4）状态估计总目标函数值T13

式（10）和式（11）中，n 为量测数目；xˆ为状态量的估计值；h（xˆ）为第i个量测相对于状态量估计值的非线性函数值。

4.2 状态估计抵御粗差能力

采用式（9）～式（12）指标来衡量状态估计计算精度，其结果如图3和表1所示，其中Agri1为基于SCADA量测的加权最小二乘状态估计，Agri2为本文所述的基于分段线性权函数的选权迭代状态估计。

图3 G指标曲线

图3为边界系数a取2.5，b取11.5，c取10.6时指标G的曲线。其中横坐标表示门槛值s，取量测误差标准差的整数倍；纵坐标为状态估计精度指标G，取值为(0，1]。

表1 不同时刻两种算法的T11、T12、T13指标值

表1为不同时刻断面下两种算法的T11、T12、T13指标比较结果。其中量测断面总数为10，按照状态估计每5分钟计算周期获得。

从图3的G曲线上可以看出，在量测系统粗差和正常量测均已确定的情况下，若状态估计计算精度较高，则能使仅含粗差的量测残差较大，而正常量测的残差很小，G指标趋向于1；若状态估计的精度较差，或者没有能够完全剔除所有量测系统粗差影响，则没有被剔除粗差将对其他正常量测进行污染，导致正常量测的残差上升，则G指标下降，如图3中当门槛值取3时，此时加权最小二乘估计法的G指标为0.69，而采用本文方法后G指标为0.81，落在3门槛值以内的量测点数增多，算法所表现的抵御粗差能力更好，因此采用本文算法其估计精度较之传统方法较好。

对于2015年2月19日9点5分的时间断面上，采用本文方法后总体目标函数由66.48降为62.29，表明估计残差进一步缩小。因此，从表1不同时间断面指标所呈现的趋势来看，在全局效果上，状态估计的总目标函数、有功目标函数等性能指标相比传统加权最小二乘估计方法减小，因而其估计的精度得以提高。