基于模糊控制电控空气悬架车身高度控制策略研究

2018-01-15关欣

装备制造技术 2017年11期

关欣

随着汽车技术的快速发展，电控空气悬架越来越多地应用于汽车当中。为了提高汽车行驶的综合性能，需要设计模糊控制器控制汽车行驶时的车身高度，使汽车高速行驶时，电控空气悬架控制车身高度降低，以减小风的阻力，提高汽车的经济性与稳定性。当汽车在颠簸的路面上行驶时，控制车身高度升高，提高车辆的通过性.

1 电控空气悬架数学模型

电控空气悬架主要由空气压缩机、储气罐、充气阀、空气弹簧、排气阀、减震器组成。空气悬架充气时，ECU控制充气阀打开排气阀关闭，储气罐中的空气充入到空气弹簧中；空气悬架排气时，ECU控制排气阀打开，充气阀关闭，空气弹簧中的空气排入到大气当中。

1.1 管路流量数学模型

空气在空气悬架中流经充排气阀产生的空气质量流量对空气弹簧的非线性特性有着重要的影响[1]，空气质量流量公式如下：

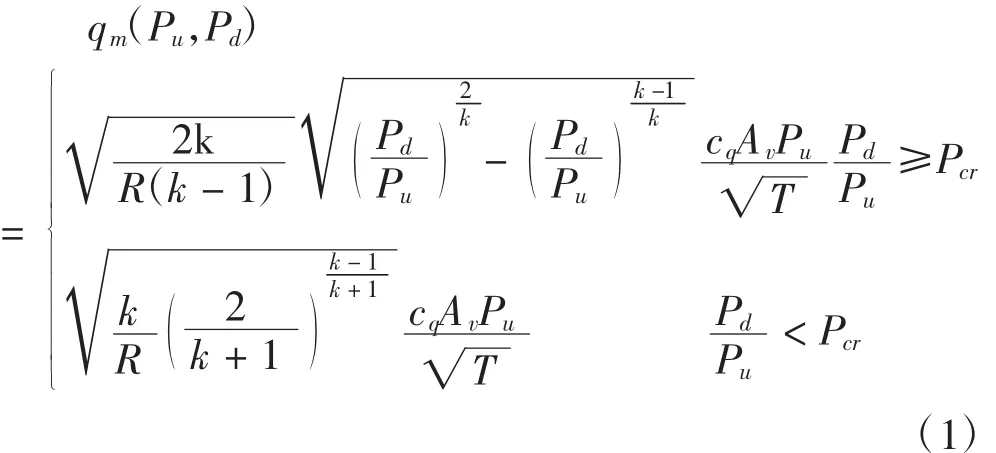
式中：R为气体常数，cq为气路流阻系数，Av为电磁阀等效截面积，T为气体热力学温度。当充气时，Pu为储气罐压力，Pd为气囊内绝对压力。当排气时，Pu为气囊绝对压力，Pd为大气压力，Pcr是临界压力比，对理想的气体，取Pcr为0.528 2.

1.2 空气压力数学模型

根据文献[2]充气过程中，空气弹簧的压力模型为

式中：V（y）＝ V0+ βy，V0为空气弹簧的初始体积，β为空气弹簧体积变化率，y为空气弹簧位移，v为空气弹簧位移变化率。

排气过程中，空气弹簧的压力模型为

1.3 空气弹簧动力学数学模型

空气弹簧在工作过程中，簧载质量受到气体压力、减振器阻尼力、重力以及惯性力作用。

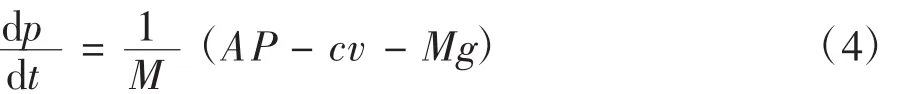
式中：M为簧载质量，c为减振器阻尼。

1.4 电控空气悬架系统Simulink模型

根据式（1）~（4）应用 Matlab/simulink 软件建立电控空气悬架系统模型如图1所示。

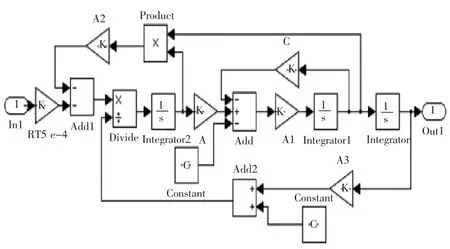
图1 电控空气悬架系统simulink模型

图中输入in1为中的空气质量流量，输出out1为车身高度。第一章中建立的模型均为数学模型，1.4中simulink模型为根据数学模型建立的，图1中in1为空气质量流量qm，add1口的输出为公式（4）中的-kRTqmu-APv，out1输出为车身高度x，A3模块为β为空气弹簧体积变化率，constant1为空气弹簧的初始体积V0，计算得add2的输出为V（y），所以Divide右端为dp/dt.intergrater2右端为p.模块A为空气弹簧截面积，constant为Mg，intergrater左端为垂向速度v，模块 c为公式（4）中阻尼，模块 A1为公式（4）中M，intergrator1左端为公式（4）中车身垂向加速度dv/dt.所以图1为根据数学模型公式（1）~（4）建立的simulink模型。

2 模糊控制器的设计

由于空气悬架充放气过程是非线性的，车身高度的控制很难根据精确地用参数来实现。设计了适用于非线性控制、鲁棒性能较好、不依赖精确物理参数的模糊控制器[3]。

模糊控制器的输入变化量1为实际高度与目标高度的高度偏差e，输入变化量2为高度偏差的变化率ec.输出量为空气悬架系统中流经管路的空气质量流量。模糊控制器输入输出框图如图2所示。

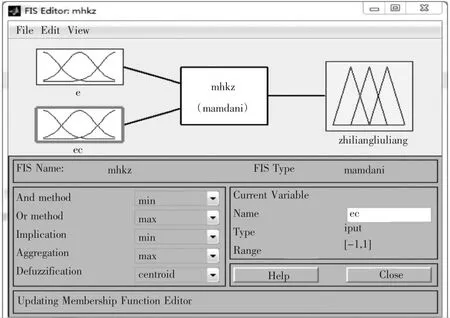
图2 模糊控制器输入输出框图

输入变化量 1取 7个模糊子集{SS，S，SM，M，LM，L，LL}.高度偏差取值范围为 0~0.03 m，论域为[0，3]，量化因子为100.输入变化量2取5个模糊子集{NL，NS，ZE，PS，PL}，偏差变化率取值范围为-0.1 m/s~0.1 m/s，论域为[-1，1]，量化因子为 10.模糊控制器输出量为空气悬架系统中流经管路的空气质量流量。输出量取 7 个模糊子集{SS，S，SM，M，LM，L，LL}。输出量取值范围为 0-1×10-8，论域为[0，1]，量化因子为1×10-8.

建立模糊控制的规则如表1所示。

表1 模糊控制规则

3 系统仿真结果

应用Matlab/Simulink软件对空气悬架模型及模糊控制器建模仿真，模型如图3所示。

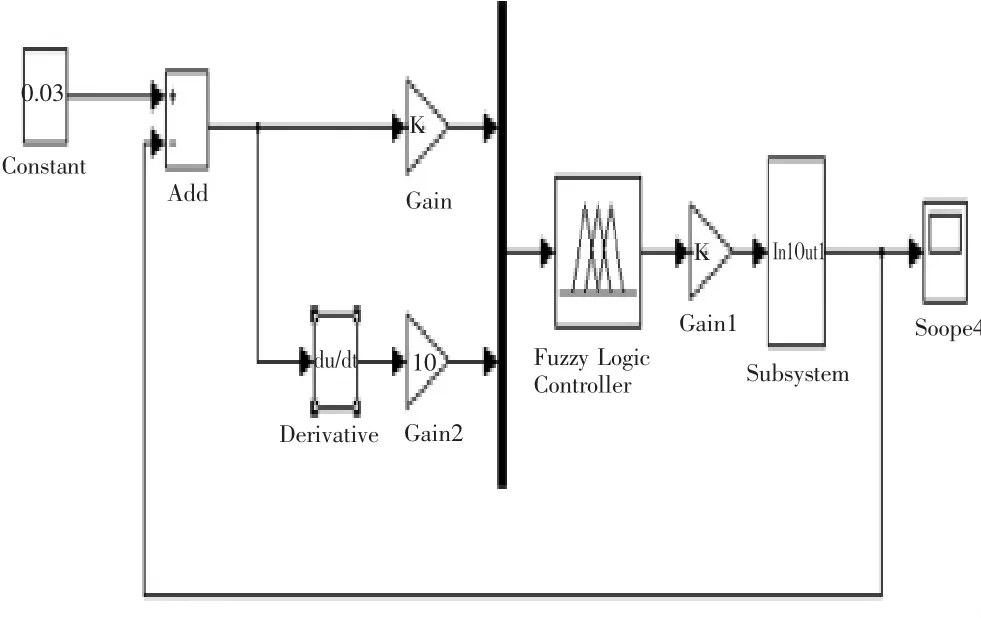
图3 电控空气悬架系统simulink仿真模型

图3 中Fuzzy Logic Controller为所设计的模糊控制器，Subsystem 为根据公式（1）~（4）建立的电控空气悬架模型。空气悬架系统所采用的参数：簧上质量为328 kg，最大的减震器阻尼系数为3 500 N·s/m，空气弹簧有效截面积为0.009 m2，空气悬架容积变化率为0.046 m3/m，电池阀有效面积为0.000 004 m2，气体热力学温度为293 K，气体常数为287 J/（kg·K）.见图 4、图5.

图4 充气过程车身高度控制响应

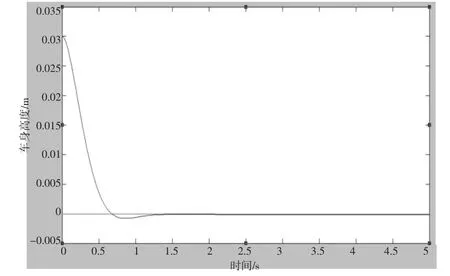
图5 排气过程车身高度控制响应

图2 与图3分别为模糊控制充气与放气时车身实际高度随时间变化的响应。图4为0 s开始，车身目标高度由“中位”0处变到“高位”0.03 m处，车身实际高度根据模糊控制规则也变化到“高位”处，经过1 s，车身高度达到目标高度，并保持稳定状态。图5为0 s开始时，车身目标高度由“高位”0.03 m降到“低位”0处，车身根据模糊控制规则也变化到“中位”处，经过0.7 s，车身达到目标高度处产生了微小的超调，1.2 s处，车身稳定在目标高度处。结果表明，模糊控制器能对车身高度稳定调节，且无过充过放现象。