基于MATLAB与ADAMS的贝克曼梁五杆机构优化设计及仿真

周瑞浩，李 宗

目前路面弯沉值检测有多种方法，文献[1-2]介绍了激光多普勒弯沉仪、落锤弯沉仪（FWD），它们都属于路面无损动态检测，但是测得的弯沉值必须要与贝克曼梁弯沉值进行对比，而我国尚未对该项工作展开深入研究。在国内弯沉检测主要采用人工贝克曼梁法，检测效率低，劳动强度大，因此，为了提高检测效率，设计了基于光电贝克曼梁的自动弯沉检测机构，本文所述的五杆机构为其中的水平升降机构。为了使得该五杆机构能够符合工作要求，须对五杆机构进行优化。文献[3]中提出的了运用复合型法建立数学模型，采用MATLAB软件与VB软件编程进行机构的优化和运动仿真分析；文献[4-6]中提出基于MATLAB优化工具箱函数多约束下的优化方法；文献[7]中提出了自主研发的通用优化设计软件系统SiPESC.OPT，采用随机优化算法-梯度优化算法相结合，使用GA、SQP和SLP多种算法组合的优化计算；文献[8-9]中介绍了可视化界面的ADAMS优化及运动仿真分析方法。本文中的五杆机构为贝克曼梁弯沉检测机构中的升降机构，为了使贝克曼梁在检测过程中保持水平的升降，因此需要对五杆机构的长度进行优化，使弯沉检测机构到达工作要求。

1 机构的运动分析

为了满足客观条件的水平运动，设计五杆机构如图 1、2所示，初始位置图 1 中 O’C’为机架，A’O’长度为 L1，O’B’长度为 L2，O’C’长度为 L3，B’D’长度为 L4，A’F’长度为 L5，E’F’长度为 L6，C’D’长度为L7，C’E’长度为 L8.

图1 连杆机构终点位置

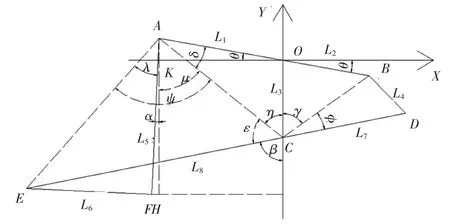
图2 连杆机构运动简图

由图1连杆机构终点位置的几何关系可知：

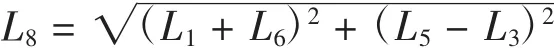
由图2连杆机构的运动简图几何关系可知：

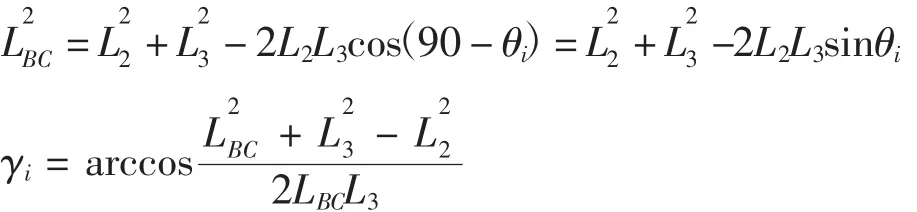
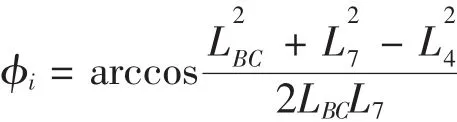
βi= γi+ φi

所以E点纵坐标在角θi的值：

Yei=-L8cosβi-L3

αi= ψi- λi- μi

∴ LAH＝ L5cosαi

∵ LAK＝ L1sinθi

∴LKH＝LAH-LAK

所以F点纵坐标在角θi的值：

Yfi=-（LAH-LAK）

根据设计问题的要求，连杆AB转动取10个离散点，目标函数按照为使得连杆EF在下降过程中保持水平稳定建立，即使E、F两点纵坐标值之差的均方根最小：

式中，Yei、Yfi为连杆EF上E、F两点纵坐标值。

2 五杆机构优化设计数学模型建立

2.1 设计变量

从上述公式中可以看出minf（X）是L1、L2、L3、L4、L5、L6、L7、L8的函数，其中 L8非独立变量，因此定义独立设计变量 X=[L1、L2、L3、L4、L5、L6、L7].

2.2 目标函数

在优化过程中，为了连杆EF保持水平状态，分别以minf（X）作为目标函数。

2.3 约束条件

2.3.1 边界约束条件

从结构的整体布局分析，各种几何尺寸的五杆机构都受其结构形状和位置的限制，即条尺寸变化必须在每个设计变量的范围内，也应该给出限制，限定条件如表1.

表1 设计变量范围

2.3.2 机构存在的条件

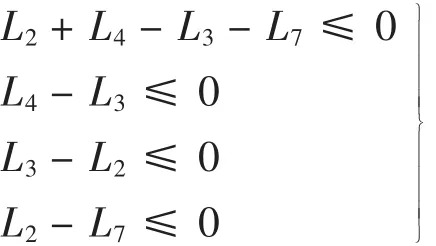
在多边形AOCEF中：

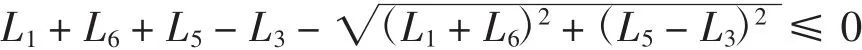
3 优化方法和仿真分析

3.1 优化函数

对于该七维约束非线性优化问题，可采用MATLAB的非线性约束优化函数fmincon求解，该函数的数学模型为：[x，fval]=fmin con（@fun，x0，A，b，Aeq，beq，Lb，Ub，'nonlcon'，options）其中 x 是目标函数的最优解；fvall是对应于该解的函数值；@fun是调用目标函数的函数文件名；x0为初始值，它的取值必须符合约束条件的要求；A为线性不等式约束条件的系数矩阵；b线性不等式的常数向量。

经过计算得到结果如表2所列。

表2 计算结果

3.2 五杆机构的验证模型

由于机构较为复杂而且设计变量较多，因此需要对优化后的结果是否满足设计要求进行运动的特性分析，传统的做法是根据五杆机构的几何关系分别求出水平杆EF两点的速度、位移表达式，然后用曲线表示出来，这种作图方法精确，但是推导过程比较复杂且计算量大。机械系统动力学仿真分析软件ADAMS为这类问题提供了方便快捷的途径，使用交互式图形环境创建机械系统几何模型，其求解器采用多刚体系统动力学理论中的拉格朗日方程，求解系统运动学方程，输出位移速度加速度和反作用力曲线，已在机械行业中得到广泛应用。

根据MATLAB优化后得到的结果，在ADAMS的交互式图形环境中建立起五杆机构的几何体，然后依次添加约束副和驱动副，完成虚拟样机模型如图3所示。

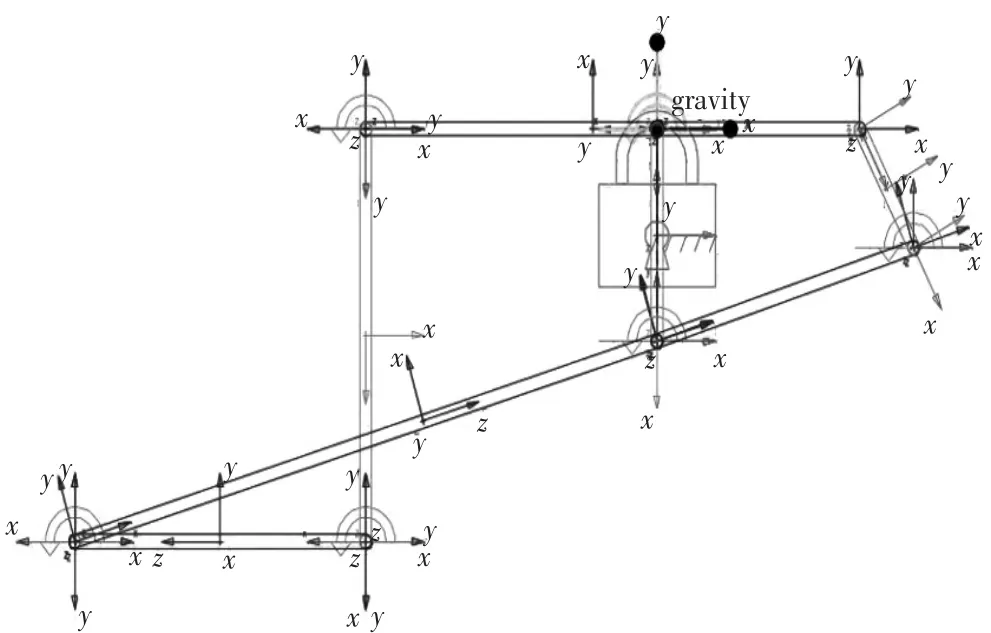
图3 五杆机构仿真模型

并创建测量函数Function分别得到E、F点的Y坐标随时间的轨迹及E、F点Y坐标差值随时间的轨迹如图4所示，3条曲线其中，Ye代表点E的Y坐标值随时间曲线，Yf线代表F的Y坐标随时间的曲线，SUBTRACT线代表E、F两点Y坐标值随时间的差值。由此可以看出，在运动过程中连杆EF基本保持水平状态，因此优化参数合理。

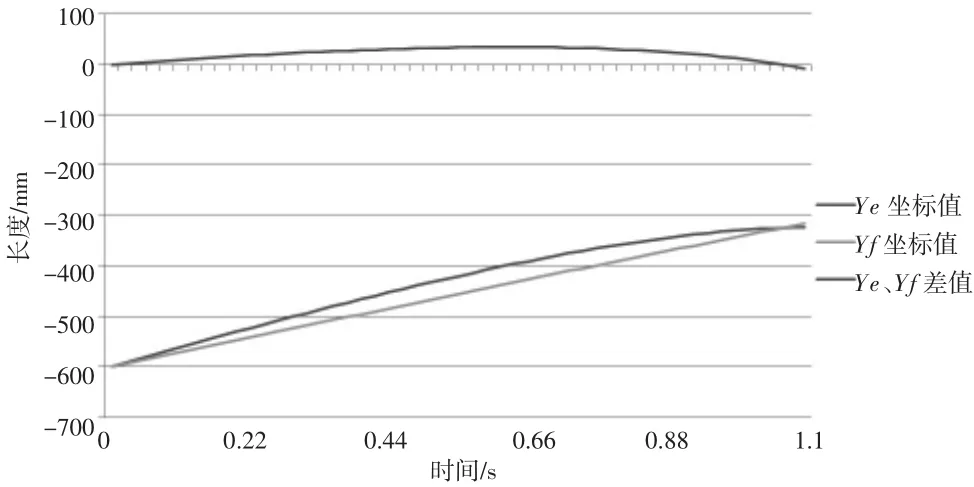
图4 E、F点轨迹图

4 结论

（1）对五杆机构进行了运动分析，建立了该机构的运动分析数学模型；根据运动分析的结果，利用MATLAB的遗传算法工具箱对机构进行了优化设计。

（2）利用ADAMS软件对优化结果进行了运动仿真，仿真结果表明：连杆EF在上升过程中两端点Y值随时间函数曲线相差微小，两者差值趋近于零，即EF连杆在上升下降过程中能基本保持水平状态，满足工作需要。

[1]张东波.基于贝克曼梁的后插式自动弯沉检测系统研究[D].西安：长安大学，2014.

[2]王 威.激光自动弯沉仪弯沉检测指标的研究[D].长沙：长沙理工大学，2013.

[3]刘晓敏，贾 媛，陈智钦.基于MATLAB与VB的六连杆内滑块机构优化设计[J].中国工程机械学报，2014，12（6）：2-4.

[4]何 俊，冯 鉴.基于MATLAB的平面连杆机构预定轨迹优化设计[J].煤矿机械，2010，31（03）：37-38.

[5]黄鹤辉，陈 晨.基于MATLAB的飞剪机构设计及优化[J].锻压技术，2003（4）：3-4.

[6]于松周，张立军，姜 浩.基于MATLAB的机器人手部连杆优化设计[J].机械设计，2014，31（5）：1-3.

[7]杨春峰，张 盛，李云鹏，等.机械压力机六杆机构优化设计[J].大连理工大学学报，2013，53（1）：2-4.

[8]郭卫东.虚拟样机技术与ADAMS应用实例教程[M].北京：北京航空航天大学出版社，2008.

[9]宋少云，尹 芳.ADAMS在机械设计中的应用[M].北京：国防工业出版社，2015.