基于优化的Fibonacci-MPPT的光伏并网控制方法研究
2018-01-12陈文王树林熊雄叶杰
陈文, 王树林, 熊雄, 叶杰
(1.华中科技大学 中欧清洁与可再生能源学院, 湖北 武汉 430074; 2.中核兰州铀浓缩有限公司, 甘肃 兰州 730065; 3.华中科技大学 自动化学院, 湖北 武汉 430074)
0 引 言
太阳能由于其储量大、环境友好以及分布范围广的优点在传统化石能源危机的背景下进入人们的视野。太阳能发电系统中,简单准确的光伏电池模型是非常重要的,也是目前限制系统效率的瓶颈;在最常见的两级式系统中,最大功率点跟踪作为前级阻抗匹配的控制策略来移动电池阵列的工作点;逆变并网部分则保证输出质量高的与电网电压同步的并网电流。
文献[1]在传统跟踪方法上基于功率电压曲线的切线角正统值进行步长优化,但运算复杂对嵌入式系统性能要求高;文献[2]介绍了常用的PI电流控制,但并网电流随电网干扰而质量差,引入的解耦控制较复杂。针对上述两个方面,通用的光伏电池模型的基础上,把显著减少迭代次数的Fibonacci搜索寻优引入到最大功率点跟踪中,然后在并网模型的基础上引入了电网电压前馈与准比例谐振控制以提高并网电流质量,取得了较好的控制效果。
1 系统模型
1.1 Fibonacci搜索算法的基本原理
为了得到光伏系统的最大输出功率,本文研究了一种新的最大功率点跟踪算法,该算法源于著名的Fibonacci数列{cn}[3],n=0,1,2,…;其通用表达式如下:
c0=0,c1=1,cn=cn-1+cn-2(n≥2)
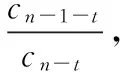
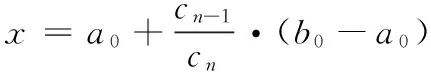
(1)
(2)
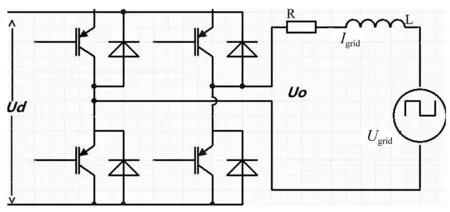
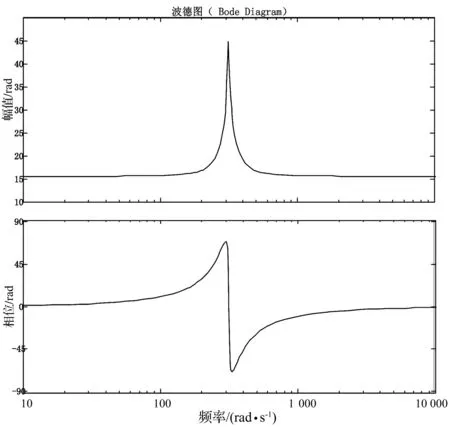
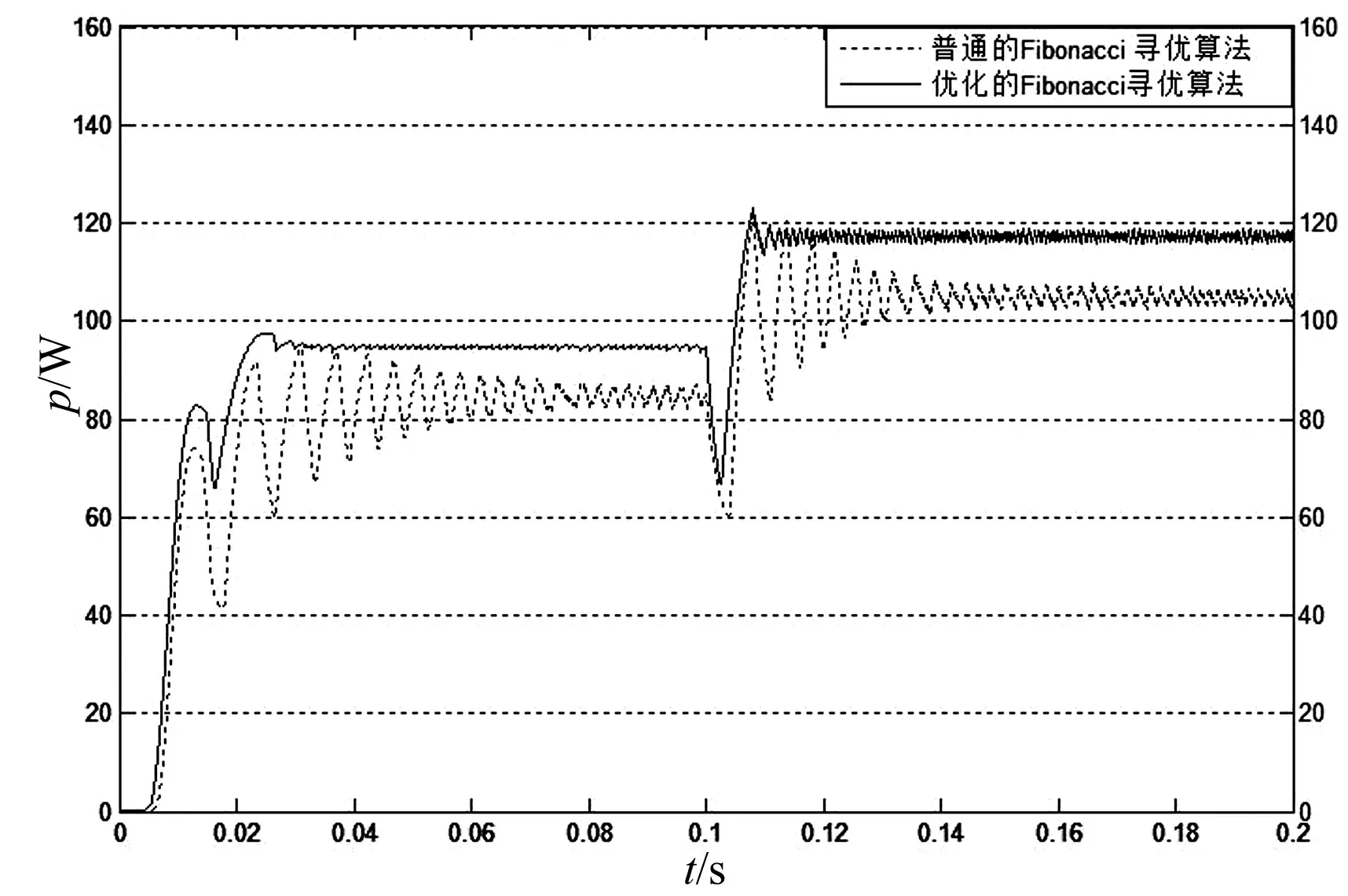
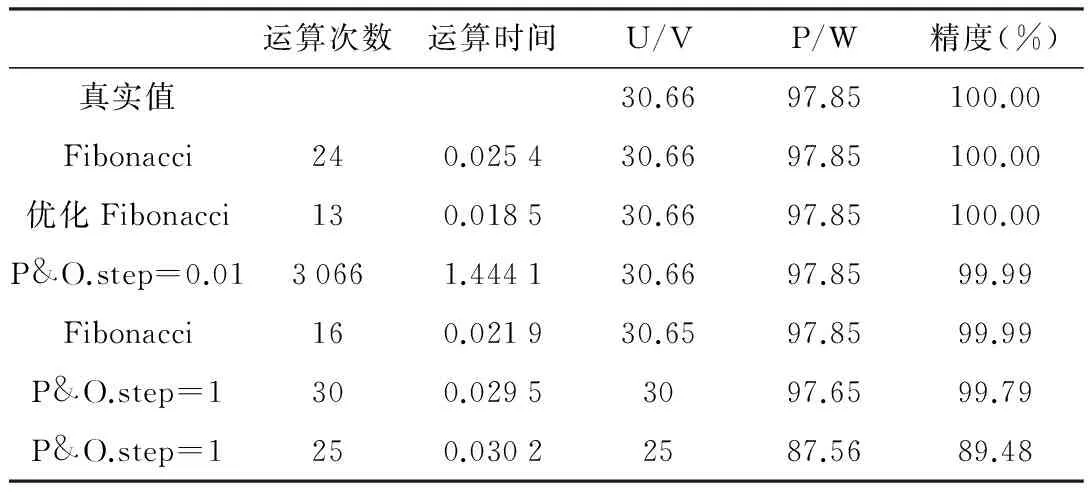
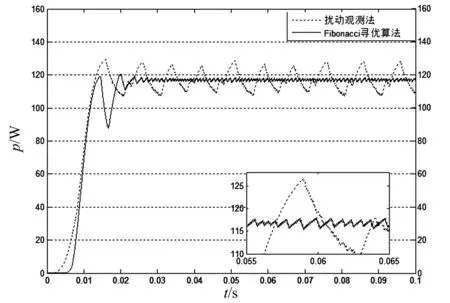
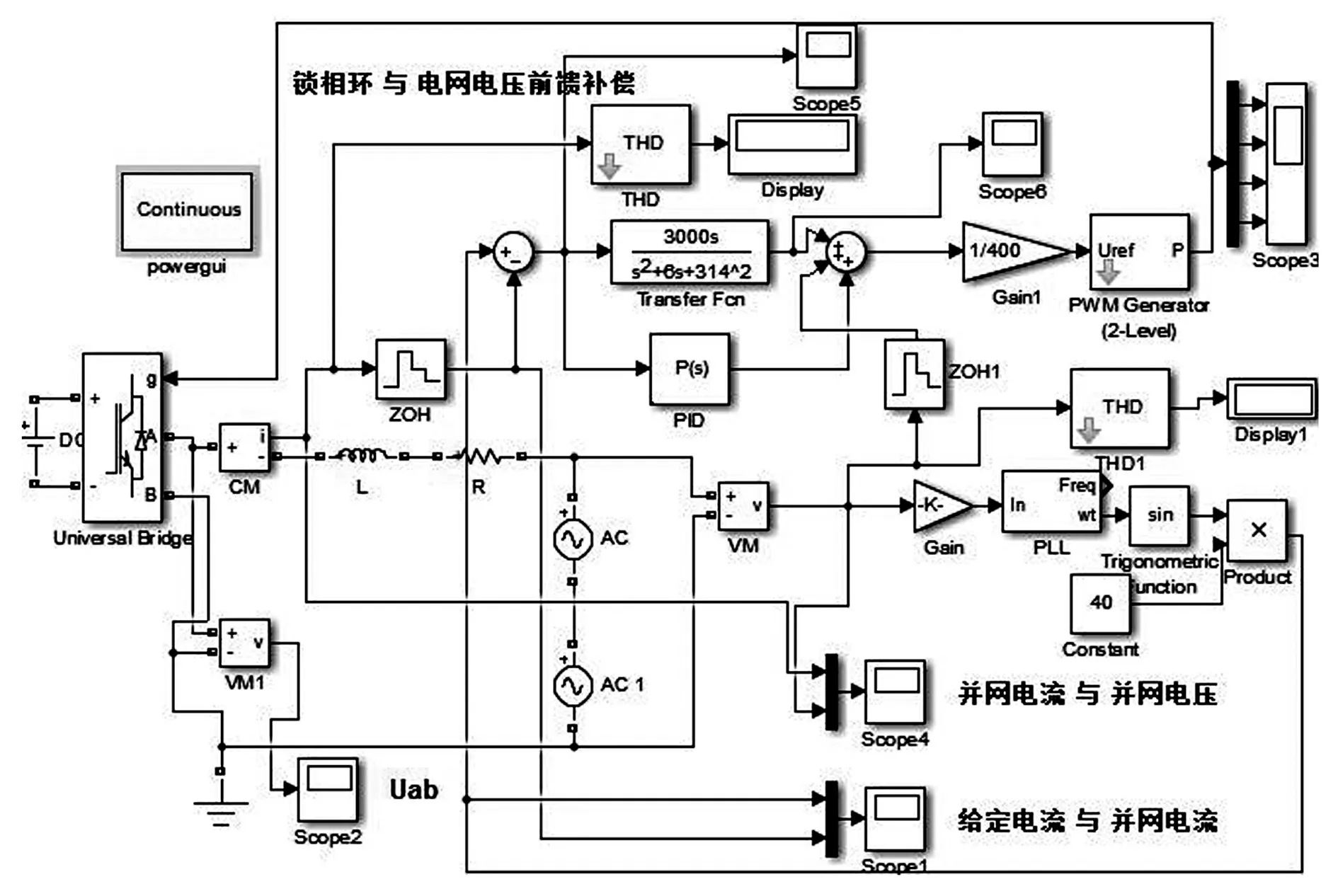
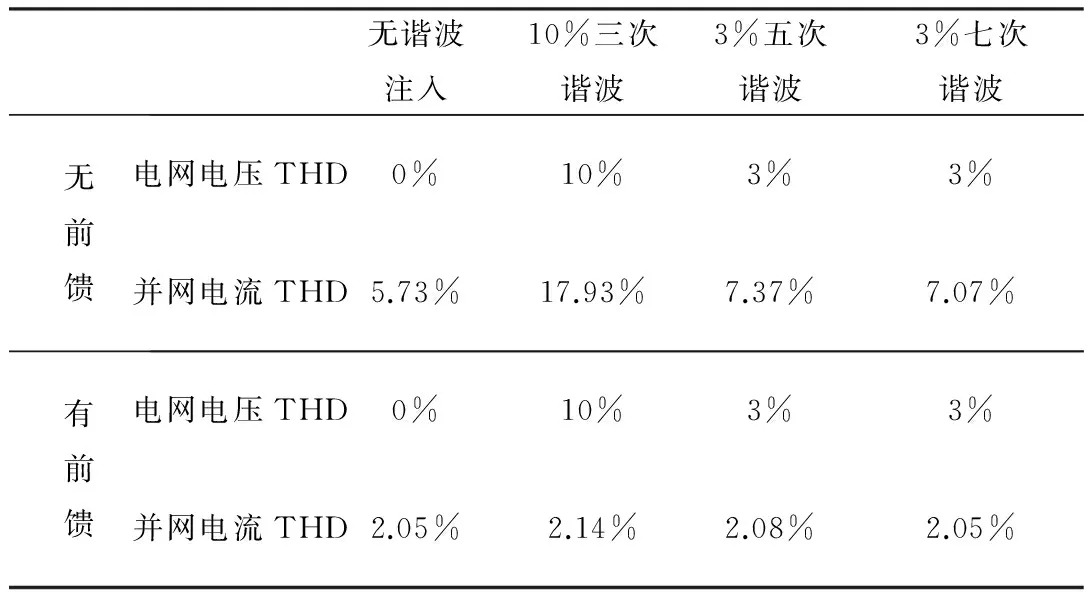
搜索过程如图1所示,对一个在区间内单峰的函数f(t), 若在[a0,b0]内存在两点x,y,满足x 图1 单峰函数搜索图示 经过多次搜索之后,要求使最终的探索点与最优解之间足够小,一般取最后一次探索得到的x,y值满足:y-x<ε,其中,ε为误差值。 如图2所示,优化的Fibonacci-MPPT控制模型在原来的一般性的Fibonacci-MPPT模型上改进了三点: (1)初始边界选择离电池参数Vm更近的范围;一般性的Fibonacci-MPPT模型的初始边界选择[0,Voc],但是由数据统计显示,在辐照和温度变化时,最大功率点的电压波动范围就在STC条件下的Vmpp附近,实验结果显示初始边界离Vm过远或过近都会使得寻优过程不精确,稳定性变差,通过实验选择一个合适的初始边界,能极大地降低寻优迭代次数,保证寻优算法的稳定性和精确性。 图2 优化后的Fibonacci寻优流程图 (3)Fibonacci线性搜寻法经过多次搜索后要与最优解足够小,设定一个精度值,越小越好,当x和y之间的差值小于这个值时,搜索结束,输出大的那个功率值,这样可以保证寻优值更接近于最优解。 优化后的Fibonacci-MPPT流程如图2所示。光伏输出功率与电压的函数可以看作在某一区域[a0,b0]内的单峰函数。在搜索之前需要先测量光照和光强的变化,通过光伏单体电池模型中的dI和dV变现出来。 基于两级式非隔离型的光伏发电系统逆变并网结构如图3所示,一般采用电压源输入,电流源输出的控制方式。输出滤波器可以隔离输出器输出电压与电网电压,调整输出电压幅值与相角以使并网电流与电网电压同步。 图3 光伏发电系统逆变并网部分结构图 电网中偶尔会混入不可预知的谐波干扰,可能会出现不对称或者畸变[5]等情况,干扰光伏系统的正常工作。在电流内环控制的基础上,为了减少Ugrid波动对逆变Igrid的影响,引入了Ugrid前馈控制。 图4 电网电压前馈控制结构图 系统的控制框图如图4所示,其中GN(s)为电网电压前馈环节,给定电流iref,实际输出电流i,偏差电流送入PI调节器Gpi(s),与前馈环节的输出送入逆变控制环节Ginv(s),最后GL(s)是滤波环节。系统的输出并网电流在前馈环节加入的情况下为, (3) 在没有引入电压前馈时,整定的电流内环PI控制器的Bode图在电网基波频率处的增益较小,在追踪正弦电流时,会存在一定稳态误差且抗干扰能力差[6]。在进行并网时,其稳态误差(相位误差)会对逆变器的功率因数造成影响。为了克服这一点,本文设计了一种基于比例谐振的PR控制策略。利用PR控制器的比例谐振来增大所控制信号在特定频率处的增益,从而消除PI控制器在追踪参考电流时产生的稳态误差。 (4) 图5 整定后的准谐振控制器频率特性 由于太阳光照实时变化的特性,选取比较有代表性的光伏组件的温度40.5 ℃;图6为光照由800 W/m2上升至1 000 W/m2的仿真实验结果,把优化后的Fibonacci寻优功率输出曲线与一般寻优功率输出曲线进行对比,可以得出优化后的Fibonacci寻控制法在快速性和精确性上都有很大的提升,也很好地减弱了输出功率的振荡问题。 图6 优化的Fibonacci-MPPT和一般性的Fibonacci-MPPT法控制下的系统输出功率对比图 为了检验Fibonacci-MPPT方法的跟踪特性,在光照强度为1 000 W/m2下,通过“数据统计信息”找到其对应的理想最大功率点电压与功率分别为31.3 V,120.7 W。 表1 P&O法与Fibonacci寻优法的精度表 如表1所示,优化的Fibonacci寻优法在运算13次后,便已经达到了100%的精度,比一般性的Fibonacci寻优法更快速,而以精度见长的扰动观测法却在3 066步时也还是与最大功率点有些许差异,当然这种精度要求在实际应用中过于苛刻,而且时间长达1.444 1 s。然而,当Fibonacci在21.9 ms时,其精度已经贴近高精度的扰动观测法。而此时大步长应用快速性的扰动观测法则也需要30步才能达到99.79%的精度,而且无法继续提升。可以看到,在25步时,其精度89%几乎是不可用的。由此可以看出,在数值理论分析下的寻优比较下,优化的Fibonacci几乎可以以快速性与准确性两方面的优于扰动观测法。 图7 优化的扰动观测法与Fibonacci-MPPT法控制下的系统输出功率对比图 如图7所示,实线、虚线分别代表负载在优化的Fibonacci-MPPT方法与优化的扰动观测法的控制下的功率曲线,优化的扰动观测法虽然在跟踪速度上有了很大的提升,几乎与Fibonacci-MPPT法相近,但在系统输出的功率曲线上出现复现的振荡,这是由于,其为寻找最大功率点而设置的步长无法最终收敛于某一点,而总会在(Um,Pm)点左右波动,由此,而根本无法稳定于MPP,也可由图7中负载上的电压抖动观察出来,由此可以看出,在实际的光伏应用中,Fibonacci-MPPT的快速性与准确性较好。 图8是在simulink中搭建的光伏并网逆变控制部分的模型,其中加入了前馈控制和准谐振控制。为了对比电网被注入谐波污染后,电网电压前馈控制的性能,分别在基本的仿真模型上注入10%的三次谐波,3%的五次谐波,3%的七次谐波,并与无谐波注入时的状态进行对比。 图8 Simulink下光伏并网逆变控制框图 无谐波注入10%三次谐波3%五次谐波3%七次谐波无前馈电网电压THD0%10%3%3%并网电流THD5.73%17.93%7.37%7.07%有前馈电网电压THD0%10%3%3%并网电流THD2.05%2.14%2.08%2.05% 通过表2中八种状态的对比,可以看出,在不加入电网电压前馈控制时,THD=5.73%,即简单的PI电流跟踪无法让系统达到国家并网标准5%以下的要求,而加入电压前馈控制后,并网电流THD下降到2.05%,由此可见,电压前馈控制的加入改善了逆变部分的动态性能;当在无前馈控制的系统中加入10%的三次谐波、3%的五次谐波、3%的七次谐波后,THD已经在5.73%的基础上大幅上升,并网电流严重畸变;而相比之下,加入了电压前馈后,并网电流在谐波注入后基本维持了标准电网电压的水平,THD控制在2.2%以内,由此可见加入前馈控制后,可以明显抵消电网电压谐波的影响,提升并网电流的品质。 当电流环用准PR控制器替换了PI控制器,且未加入并网电压前馈控制时,并网电流的误差值在1.5 A左右,就可以基本消除并网电流误差。仿真结果如图9如示,而电网电压前馈控制的加入,也可以通过对电网电压干扰的克服而降低并网电流的误差,两者的基波幅值均为40 A,准确跟踪了参考电流。 图9 准谐振控制下的并网电流误差 本文在一般性的Fibonacci寻优模型的基础上建立优化的Fibonacci寻优模型;对比常用MPPT方法发现优化的扰动观测法虽简单直接,但却引起系统的可复现振荡;引入的优化的Fibonacci-MPPT方法能大辐降低寻优时间,控制好迭代误差,可以具有较好的稳定性和快速性;设计电网电压前馈控制来抑制电网谐波干扰;并设计准谐振控制器来减小并网电流的误差,都取得了较好的效果。未来针对现在发展较快的微光伏逆变器下潜力较大的反激式变换拓扑变换以及直流电压环控制等方面,还需要深入全面的研究。 [1] 王亚楠, 杨旭红, 王军成,等. 一种新型变步长光伏最大功率点跟踪控制策略[J]. 电气传动, 2015, 45(1): 54-57. [2] 赵清林, 郭小强,邬伟扬, 单相逆变器并网控制技术研究[J]. 中国电机工程学报, 2007,38(16): 60-64. [3] FANGRUI L, SHANXU D, FEI L, et al. A variable step size INC MPPT method for PV systems[C]. Industrial Electronics, IEEE Transactions. 2008, 55(7):2622-2628. [4] RAMAPRABHA R,BALAJI M.Power point tracking of partially shaded solar PV system using modified Fibonacci search method with fuzzy controller[J]. International Journal of Electrical Power & Energy System,2012,(43): 754-765. [5] 单光明. 光伏并网逆变器的滤波与控制技术研究[D]. 南京:南京理工大学,2010. [6] ZHOU YUFEI,HUANG WENXIN,HONG FENG,et al. Modelling analysis and power loss of coupled-inductor single-stage boost inverter based grid-connected photovoltaic power system[J].Iet Power Electronics,2016,1(9): 1664-1674.
1.2 优化的Fibonacci-MPPT控制模型

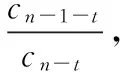
2 并网控制
2.1 电网电压干扰的克服

2.2 并网电流误差的消除
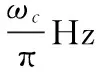
3 系统仿真
3.1 优化后的Fibonacci-MPPT性能对比
3.2 电网谐波干扰抑制
3.3 并网电流误差消除

4 结束语
