电力通信网结构优化及拓扑生成算法
2018-01-12李周许红升叶彬葛斐荣秀婷徐强
李周, 许红升, 叶彬, 葛斐, 荣秀婷, 徐强
(1.国网安徽省电力公司经济技术研究院,安徽 合肥 230022; 2.安徽大学,安徽 合肥 230601;3.安徽中兴继远 信息技术股份有限公司,安徽 合肥 230031)
0 引 言
电力通信网络是电力系统的重要基础设施,承载着电力调度自动化、电网生产、营销、经营等核心业务。日前,国家电网公司提出地县一体化运作模式,其总体目标是推进地县调度系统与运行设备的整合,建立一体化的调度运行管理平台[1-2],改变各个调度系统运行水平参差不齐的现状,促进技术资源、设备资源、数据资源的共享,适应智能电网发展要求[3-5]。
在该背景下,地县公司各自建设、独立成网的传统局面逐渐向地县一体、统一调度的建设模式过渡。例如,通信业务的数量及范围发生巨大变化;网络节点不断扩充、层次逐渐增加、拓扑结构更加复杂[6]。而现存网络中存在许多缺陷,无法满足电网发展的需要,如设备品牌不统一、局部地域带宽闲置、可扩展性不足等[7-8],迫切需要进行结构优化。
目前主流的网络拓扑生成模型主要是建立在随机模型、层次模型或幂率模型的基础上[9]。随机模型生成的网络拓扑的节点随机分布[10],与电力通信网络不符;层次模型与SDH电力通信网多层级(如核心层、骨干层、接入层)的特征符合;幂率模型生成的拓扑与真实的网络更加接近,能够较好地反映节点的度的分布[11]。如何建立一个能够反映电力通信网络更多特征的模型是需要继续研究。
本文从电力通信网络的现状以及电网发展对网络性能的新要求出发,建立了一种基于图论数学模型的算法,将实际网络的物理模型转换为计算模型,该图论模型将电力通信网络看成一个无向图,图中节点代表网络设备,边代表通信链路。在算法中,根据SDH网环形结构的特点,提出建立多个辅助圆的思想,网络节点在辅助圆上呈向外辐射式分布,很好地表现了地县一体化网络多层拓扑结构的特点,改变了传统(手工)绘制拓扑图方式。此外,针对现有网络的缺陷,提出了一系列网络优化策略,对现有网络进行诊断和评估。
1 网络结构优化
1.1 网络优化原则
以安徽地区通信网为例,本文算法采取了以下几点优化方法:(1)对地县网络统筹规划,统一组网。采用核心层-接入层拓扑结构,适当增加小核心层。增大核心层带宽。所述小核心层实质上还是接入层,只是升级了分布在该层上的传输设备的通信容量,便于节点接入。(2)网络的拓扑形式为环型拓扑和线型拓扑的结合模式,以环型拓扑为主,充分利用SDH环网的自愈功能,建立通道保护或复用段保护机制,提高网络的安全性能。(3)对冗长环路进行拆环重组,提高抗单点失效性(4)汇聚方式采用两点汇聚和单点汇聚相结合,以双点汇聚为主,提高组网灵活性。
1.2 组网边界条件
结合国网公司“十三五”地市骨干传输网优化指导意见,可将以下组网原则作为边界条件。
(1)通信网带宽资源预留不低于30%。(2)接入环(链)站点数量大于7个时宜选择2.5 Gb/s速率,不大于7个站点的环和末端分支,一般选择622 Mb/s速率,如果是小核心层,选择2.5 Gb/s速率。(3)核心层节点数量一般不超过全网站点数量的15%。由此可以测算出电力通信网络带宽需求情况如表1、表2所示。
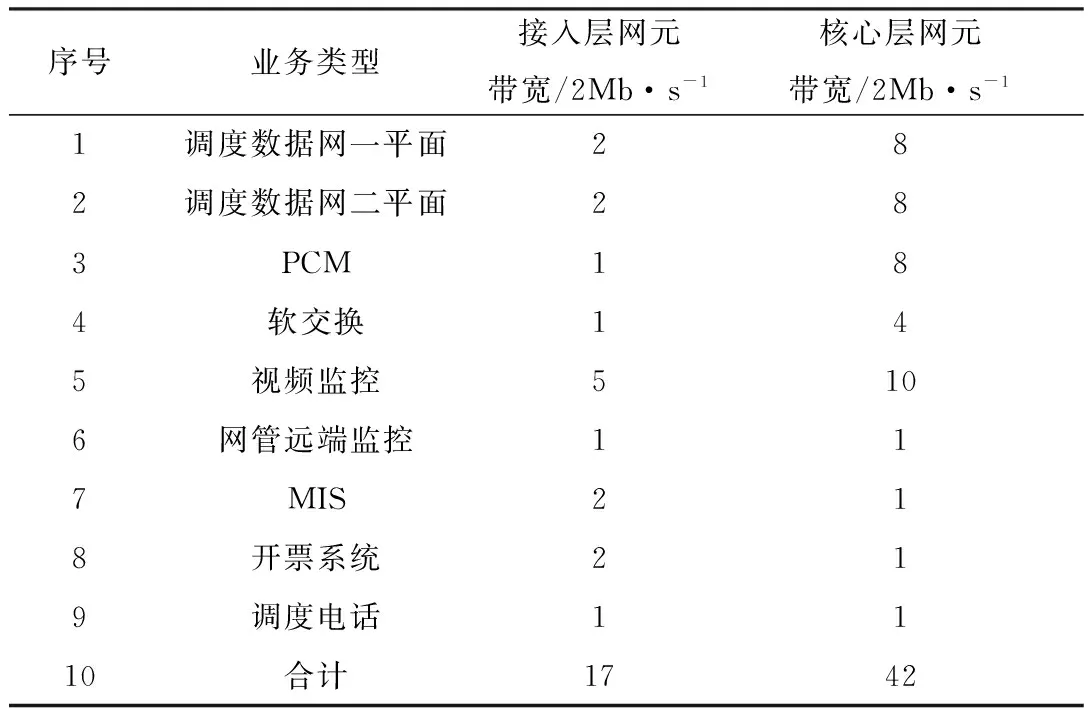
表1 接入层与核心层网元业务带宽资源
本文在研究网络结构优化时,主要考虑总带宽资源为2.5 Gb/s(即1 008*2 Mb/s)的情况,根据前面所述边界条件和表1,并结合工程实际,分析得出表2所示网元数量临界分布情况。
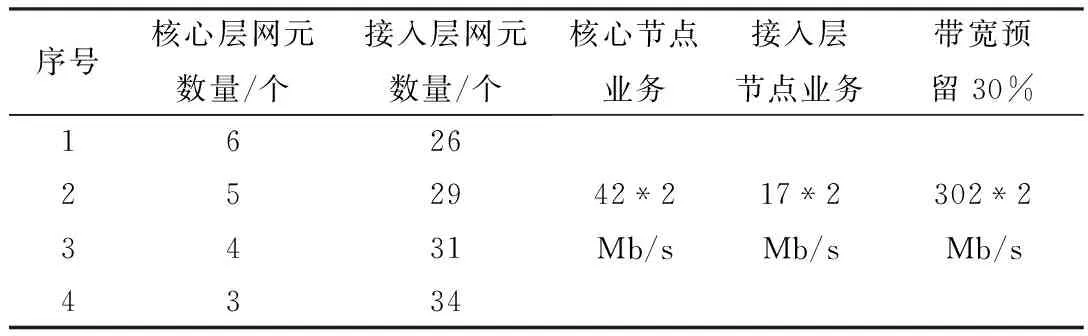
表2 2.5 Gb/s环网网元数量临界分布情况
2 图论数学模型
本文在MATLAB开发平台上建立一种图论数学模型,实现网络拓扑的自动生成。该模型在直角坐标系中绘制多个同心圆,称之为辅助圆C,每个辅助圆代表网络拓扑的一层结构,网元分布在辅助圆上。同时,辅助圆的数量不受限制,这决定了网络的层次是不受限的,便于扩展,可以满足地县一体化调度模式下多层拓扑的要求。通过借鉴文献[12]中所述邻接矩阵的概念,本文研究发现,辅助圆为获取节点位置提供了方便的同时,其环形结构的特点,也使得分布在上面的节点的邻接矩阵具有一定规律,根据该规律很容易求解邻接矩阵。此外,在算法设计时,运用均匀分布和无限分割的思想,使得生成的拓扑结构的节点数量不受限制,方便节点扩充的实际需求。
2.1 附图及符号说明
2.1.1附图说明
图1为本文算法生成的电力通信网络拓扑图;图2为图论数学模型辅助说明图,本文将依据该图说明图论数学模型的建立过程。图1、图2中的坐标系的横纵轴只用于衡量辅助圆半径,没有实际意义。
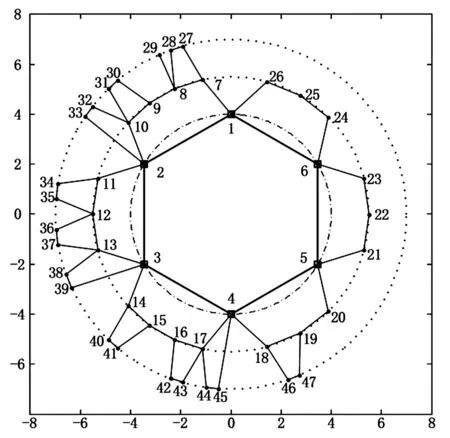
图1 电力通信网拓扑生成图
2.1.2符号说明
图1中的数字为网元的序号标注。图2中各符号的意义分别为,C1:辅助圆1;C2:辅助圆2;C3:辅助圆3;θ:圆心角;L1:核心层;L2、L3:接入层(或者小核心层);a、b:核心网元;c、d、e、f、g、h、i:子网元。变量符号有,Nc:核心网元的数量;Ns:接入层L2子网元的数量;Nt:接入层L3子网元数量;Ms:辅助圆2上各接入层子网元数量矩阵;Mt:辅助圆3上各接入层子网元数量矩阵;R:辅助圆1半径;Rr:辅助圆2半径;Rrr:辅助圆3半径;S(i,:):n阶矩阵S第i行的所有元素的集合;G:表示电力通信网中由若干链路和网元节点组成的无向图;V:V为非空集合,称为顶点集,即网元节点;E:E是V中元素构成的无序二元组的集合,即网元节点间的通信链路。

图2 图论数学模型辅助说明图
2.2 图论模型的建立
如图1所示,本文算法生成的网络拓扑图建立在直角坐标系中,图中各网元均进行了序号标注。现根据图2描述本文图论模型的建立过程。
该模型设计了三个输入参数,分别为核心网元的数量Nc、接入层子网元的数量矩阵Ms、Mt以及各辅助圆的半径R、Rr、Rrr。其中各辅助圆半径之间的关系为Rr=R+1.5,Rrr=R+3。调用相关命令在坐标系中绘制辅助圆C1、C2、C3,辅助圆的圆周角定义在(π/2,5π/2)区间。网元节点采用均匀分布,因此图2中核心层L1呈正多边形状,且每条边对应的圆心角θ=2π/Nc。各核心网元构成了一个环,该环可以看作无向图G=
S(i,:)=

据此特点,本文图论数学模型求解邻接矩阵的方法是:用zeros(n)命令构建一个全部元素均为0的n阶矩阵,然后按照上式所述规律将各行的相应元素置为1。由于核心网元在辅助圆1上呈均匀分布,故区间(π/2,5π/2)被分为Nt等份,故容易获得各核心网元的坐标值矩阵。得到了网元的邻接矩阵和坐标值后,调用工具箱中的gplot命令便可生成网络的拓扑结构。
现针对图2中Nt=6的情况举例说明核心层L1拓扑结构的生成过程:Nt=6时,核心层是一个节点数为6的环,按照上述求解网元邻接矩阵和坐标值矩阵的方法,设核心网元的邻接矩阵和坐标值矩阵分别为A、B,则:
然后调用gplot(A,B)命令即可生成核心层L1的拓扑结构。Nt为其他值时同理可求得。由于圆周角可以进行无限平均分割,故该模型在辅助圆上分布网元节点的方式,使网元数量不受限制,可满足不同的实际需求。子网元c、d、e、f构成了接入层L2,且接入层L2采用两点汇聚方式,汇聚点为核心网元a、b。从径向看,接入层L2上各子网元的分布可看作是对核心网元a、b构成的圆心角θ的平均分割,因此按照核心层邻接矩阵及坐标值矩阵的求解思路,可同理得出接入层L2的邻接矩阵及坐标值矩阵,从而生成该层的网络拓扑图。由子网元g、h构成的接入层L3亦可依照次方法绘制,子网元i为单点汇聚方式,与子网元d共同形成了“环链”拓扑形式中的“链”结构。
2.3 图论模型算法步骤
表3给出了本文图论模型的建立步骤。

表3 图论数学模型算法步骤
2.4 图论模型特性分析
从上述建立模型的过程可以看出,该模型基于图论,将电力通信网络的实际物理模型转换成计算模型,该模型根据SDH网络环型拓扑的实际特点,巧妙设计了辅助圆,每个辅助圆代表一个层级,多个辅助圆呈径向分布,与真实网络非常相近,这也是该模型与传统拓扑生成方法的很大不同之处。每个层级的辐射范围可以通过调整辅助圆的半径来改变,具有较好的模拟效果。网元均分布在各辅助圆上,使得整个拓扑图的布局清晰、层级分明,而传统的在网管软件添加网元时布局就比较随意。
算法设计时,只需要修改若干参数便可以根据需要调整接入层的汇聚方式、环型拓扑的比例,这使得本算法具有灵活的应用方式。此外,根据公式(1),可以方便地表达拓扑中节点间的关系,简化了算法的设计。
3 应用实例
为了体现本文算法的实用性,下面运用本文所述结构优化策略和图论数学模型对图3所示A地区网络进行优化。
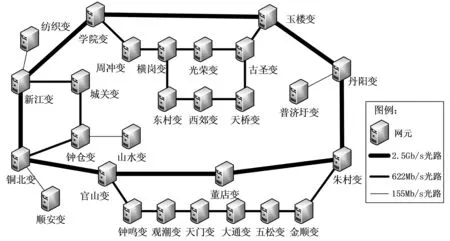
图3 安徽A地区电力通信网络拓扑图
该网络中核心网元有8个,子网元有19个,根据表1所统计的核心网元与子网元的业务带宽资源,可以知道A网共占用了8*42+19*17=659个2 Mb/s的带宽。2.5 Gb/s条件下,总的带宽资源为1008个2 Mb/s,计算得A网的带宽预留比例为34.6%,满足边界条件1所述带宽资源预留比例不低于30%;根据表2所示2.5 Gb/s条件下网元临界分布情况,可知由8个核心网元与19个子网元组成的A网不在任意一种临界情况之内,即不满足组网边界条件3;A网中部分光路的速率是155 Mb/s,不满足组网边界条件2,应当升级至622 Mb/s,以提升网络的扩展能力。
关于A网具体优化措施有:
(1)丹阳变至朱村变光路速率与核心环速率不同级,应该升级至同一层级速率。
(2)A网链型拓扑比例过多,缺乏保护机制。应将纺织变与顺安变就近接入新江变-城关变-钟仓变-铜北变环网中。普济圩变同理。
(3)学院变-周冲变-横岗变-光荣变-古圣变-玉楼变环网接入了较多子网元,从网络的节点扩充能里考虑,将该环网速率升级至622 Mb/s,构成小核心层。
(4)核心站点数过多,故将核心层速率由2.5 Gb/s提升到10 Gb/s,从而提高A网的业务承载能力。
(5)钟鸣变-观潮变-天门变-大通变-五松变-金顺变环路过于冗长,抗单点失效性差,对其进行拆环重组
本文所述图论数学模型为上述问题提供了解决方案。结合上面的分析与图论数学模型算法的步骤,可知输入网元参数有核心层网元个数Nc=8,次外层子网元数量矩阵Ms=[40403301],最外层子网元数量矩阵为Mt=[3000001],辅助圆的半径设为R=4。由Nc=8,根据式(1)可以得到核心层节点的邻接矩阵A为:

8个核心网元的坐标值矩阵B为:
调用命令gplot(A,B)即可生成核心层,如图4中的红色部分。重复执行表1中步骤S1、S2、S3、S4即可生成图3中其他部分的拓扑。图中使用不同的颜色区分不同层级的光路速率,并增加节点名称标注。
优化后的A网拓扑结构如图4所示。

图4 网络结构优化图
从图4所示网络结构优化图可以看出,由本文图论数学模型生成的拓扑图的层级清晰、界面友好。优化后的网络为三层“环链”拓扑结构,具有较好的环网保护机制,可以提高网络的安全性能。通过升级光路速率,网络的业务承载能力有了很大提高。组网方式更加灵活,小核心层的增加充分考虑到以后节点扩充的需要。对冗长环路进行适当的拆环重组,提升了网络的抗单点失效能力。
4 结束语
本文针对电力通信网络结构及拓扑生成方法及中存在的不足,提出网络结构优化原则与组网边界条件,建立了一种图论数学模型,将物理上的网络拓扑抽象为无向图。根据SDH网络环型拓扑的特点,提出建立辅助圆,总结了分布在辅助圆上的节点的邻接矩阵所呈现的规律。为基于地县一体化模式的地区电力通信传输网络架构研究提供了借鉴。
本文算法主要针对电力通信网络中只包含一个核心网的情况,需要进一步研究在多个环网条件下,如何改进和优化本文算法,提高算法的实用性。此外,可以为本文图论数学模型设计一个图形用户界面(GUI),形成一个网络拓扑生成器,增强用户体验和使用的便捷性。
[1] 张龙, 孙大雁, 赵普,等.基于大运行省地县一体化调度运行管理系统的建设[J].电力信息化, 2012,10(5): 8-12.
[2] 丁伟强, 裘卫星, 李海龙, 等.绍兴电力通信网地县一体化优化调整研究[J]. 电力信息与通信技术, 2014, 12(10): 64-68.
[3] 余贻鑫, 刘艳丽. 智能电网的挑战性问题[J].电力系统自动化, 2015, 39(2):1-5.
[4] 辛耀中, 石俊杰, 周京阳, 等.智能电网调度控制系统现状与技术展望[J]. 电力系统自动化, 2015, 39(1): 2-8.
[5] 李俊雄, 黎灿兵, 曹一家, 等.面向智能电网的互动式节能调度初探[J]. 电力系统自动化, 2013, 37(8): 20-25.
[6] 李周, 荣秀婷, 叶彬, 等.安徽电力地县一体化SDH设备网络结构优化方法[J]. 无线互联科技, 2015,15(22): 26-29.
[7] 谌志刚, 李颖.县域通信网地县一体化改造方案研究[J]. 电力信息与通信技术, 2015, 13(9): 107-111.
[8] 齐一飞, 金学东, 刘振栋, 等.烟台地区电力通信网市县一体化优化改造[J]. 电力信息与通信技术, 2015, 13(6): 120-123.
[9] JIN C, CHEN Q, JAMIN S. Inet: Internet topology generator[J]. Magnetics IEEE Transactions on, 2015, 19(3): 960-963.
[10] WAXMAN BM. Routing of multipoint connections[J]. IEEE Journal on Selected Areas in Communications, 1989, 6(9): 1617-1622.
[11] 张春环, 雷蕾, 纪越峰.一种新的网络仿真拓扑生成器[J]. 系统仿真学报, 2006, 18(11): 3115-3117,3121.
[12] 刘焕淋. 通信网图论及应用[M]. 北京:人民邮电出版社,2010.
