新疆玛纳斯河年径流频率分析

郑锦涛,陈伏龙,张鑫厚,廖 欢

(石河子大学水利建筑工程学院,新疆 石河子 832000)

年径流序列频率分析对于区域水资源管理利用十分重要[1],传统年径流时间序列频率分析要求样本时间序列满足独立同分布一致性假设,然而受到气候变化及人类活动的影响,年径流成因及影响条件变化显著,导致水文序列不再满足一致性假定,进行年径流序列频率分析时需对序列非一致性加以重视。近年来,国内外学者纷纷针对水文频率分析的非一致性进行了研究。Singh等[2]针对洪水序列的非一致性提出了条件概率分布模型,认为年极值洪水以不同的概率发生在不同的季节,利用全概率公式自季节性洪水序列推导出年极值洪水序列的频率分布形式。Singh等[3]首次将混合分布模型应用到非一致性水文频率分析,但当时对参数估计问题没有完全解决。Alila等[4]应用混合分布模型对Gila进行了研究,发现混合分布模型比传统的单分布模型更佳。宋松柏等[5]提出了基于跳跃变异的非一致性水文序列频率分析的方法,分析渭河泾河张家山站1932—2006年年平均流量序列,获得不同设计频率的设计流量值。

在玛纳斯河年径流的研究方面,陈伏龙等[6]基于玛纳斯肯斯瓦特水文站55 a水文及气象数据,采用线性回归、趋势分析及滑动平均等方法,分析肯斯瓦特站的径流和气候变化特征,并运用Mann-Kendall和累积距平法识别出1995年为径流时间序列的突变年份。常浩娟等[7]运用R/S分析等分析方法对玛纳斯河红山嘴水文站60 a的径流资料进行年际和年内径流的规律特征分析,但没有进行径流分布的一致性分析。玛纳斯河年径流分析主要集中于趋势及变异分析,分析结果只能提供年径流变化趋势等相关内容,对于玛纳斯河年径流序列非一致性分布研究较少。笔者采用Hurst指数对玛纳斯河1956—2014年径流序列的非一致性进行定量判断,采用滑动t检验、Mann-Kendall检验对序列变异年份进行识别,并构建混合分布模型和条件概率分布模型进行频率分析,为玛纳斯河设计年径流的计算提供新参考。

1 研究方法

1.1 变异点诊断方法

1.1.1 Hurst指数分析方法

标准统计分析假定系统基本是随机的,产生时间序列的过程有较大的自由度,而且序列内部的关系是极其复杂的,对其进行确定性的说明难度很大,而自然界中充斥着大量的非线性随机和确定性系统,比如河流年径流序列。为了研究这些系统,需要一种非参数的统计方法。Hurst[10]利用R/S分析研究许多自然系统,而且通过这个方法可以区分随机和非随机系统、趋势的持续、循环的持续和长期非函数周期时间序列与随机序列。

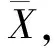
(1)

这样Z具有零均值性,由Z产生一个累计时间序列Y:

Yi,r=(Zi+Zr) (r=2,3,…,n)

(2)

由此产生新的时间序列Y,由定义可知,序列最后一个Yn,n将为0。

R/S的重标极差Rn为

Rn=max{Yi,r}-min{Yi,r}

(3)

对于Rn,下标n表明对于X={X1,X2,…,Xn}是一个调整过的极差。因为Z已经被调整为零均值,Y的最大值总是大于或等于0,而最小值总是小于或等于0。

(R/S)n=cnH

(4)

式中:c为常数;H为Hurst指数。

1.1.2 滑动t检验

滑动t检验是通过考察两组样本平均值的差异是否显著来检验突变。其基本思想是把一时间序列中的两段子序列均值有无显著差异看作来自两个总体均值有无显著差异的问题来检验。如果两段子序列的均值差异超过了一定的显著性水平,可以认为均值发生了质变,有突变发生。

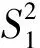
1.1.3Mann-Kendall检验

Mann-Kendall检验法是一种应用广泛的检验时间序列趋势变化及突变的非参数性检验方法。其计算方法较为简便。对于具有n个子序列的样本X,计算其统计量Uk与Bk。当Uk或Bk出在临界直线外侧时(当置信水平为95%时,临界值为1.96),否定零假设,表明上升(下降)的趋势显著。超过临界直线的部分被认为是出现变异的序列。如果曲线Uk和Bk出现交点,并且交点在临界线之间,那么交点对应的年份则为突变开始的年份。

1.2 非一致性年径流序列频率分析

1.2.1 基于条件概率分布模型频率分析方法

条件概率分布法由Singh等[2]提出,宋松柏等[5]在参考国外学者对非一致水文时间序列频率分析的基础上,依据概率论原理,考虑到水文序列可能存在跳跃变异,建立了一种便于计算的非一致时间序列频率分析模型。

假设一个时间序列容量为N,对其进行变异性诊断并对各变异点进行物理成因分析,将全时间序列划分为s个子序列。对其进行频率分析需满足以下前提:

a. 各个子序列Xi物理成因相同,服从同一分布Pi(x),不同子序列可以采用不同的分布。

b.s个子序列Xi相互独立,以下2s-s-1个等式成立,即

(5)

c. 各个子序列中水文变量X发生概率可能不同。但满足: 若{Ai}为水文变量X发生在第i个时间段内事件,则

(6)

d. {Ai}互不相容,即Ai∩Aj=Φ(i≠j;i,j=1,2,…,s)。

基于以上假定,可以推导出非一致性水文序列频率分析的条件概率分布模型。

事件B={X≤x}一定包含于事件{Ai}(i=1,2,…，s)中,根据全概率公式,非一致性水文序列的分布函数F(x)为

(7)

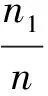
假定P(xAi)(i=1,2,…,s)连续可微,则非一致性水文序列的密度函数f(x)为

(8)

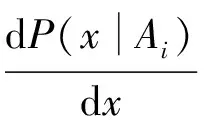
考虑到玛纳斯河水文及气象等资料相对匮乏,年径流序列长度较短,无法做到精确划分出若干个子序列,宋松柏等[5]建议将河流水文时间系列划分为两段,找到一处最为显著的变异点即可。

假设子序列长度分别为n1和n2,分别采用P-Ⅲ型曲线进行拟合,整理归纳得出全序列超过限制频率的理论频率公式如下:

(9)

式中αi、βi、a0i(i=1,2)分别为fi(x)分布的形状、尺度和位置参数。

1.2.2 基于混合分布模型频率分析方法

混合分布法最早由Singh等[3]提出,后来得到了李子远等[11]的关注,在水文频率分析中得到广泛的应用。混合分布模型假定非一致的水文样本序列由k个子序列混合而成,即:

F(x)=α1F1(x)+α2F2(x)+…+αkFk(x)

(10)

式中:Fi(x)为子序列的累积分布函数；αi为相应子序列权重系数,满足α1+α2+…+αk=1。

混合分布模型构建需要调取大量水文及气象资料对年径流成因进行详细分析,根据年径流的不同物理影响因素将年径流序列划分为相应子序列。但子序列数量越多,待估参数就会越多,参数估计难度会越大,所以子序列的个数一般保持在最低限度。由于玛纳斯河年径流时间序列较短,划分成多个子序列反而会降低参数估计的准确度,故假设混合分布模型由两个子序列组成。

关于混合分布模型子序列的划分,设间断点的初始位置为考虑物理成因不同造成的年径流序列的突变位置,但是考虑到可能存在一些隐性信息的流失,不应过分强化突变位置的固定性,所以间断点位置可能并不固定,可以根据实际需要在一定条件下进行调整。

假设非一致性全时间序列X样本数为n,变异点位置为τ。假设变异点之前的序列为X1,服从概率密度函数为f1(x)的分布;变异点之后的序列为X2,服从概率密度函数为f2(x)的分布;非一致性全时间序列X服从概率密度函数为f(x)的混合分布,即

f(x)=αf1(x)+(1-α)f2(x)

(11)

式中:α为权重系数。

SL 44—2006《水利水电工程设计洪水计算规范》规定水文变量采用P-Ⅲ曲线进行拟合。假设两个子序列服从P-Ⅲ分布,其概率密度函数f1(x)和f2(x)的表达式分别为

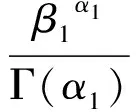
(12)

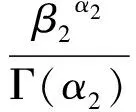
(13)

则采用超过制频率形式的混合分布的理论频率分析公式为

(14)

式中αi、βi和a0i分别为fi(x)分布的形状、尺度和位置参数。

混合分布的参数估计方法主要有极大似然估计(MLE)[12]、线性矩估计(LME)[13]和间隔最大积估计[14](MPSE)等,但传统的参数估计方法计算过程复杂并且精度不足[1]。成静清等[15]认为混合分布的参数估计可以采用模拟退火算法,模拟退火算法较传统参数估计方法运算高效且不受参数个数的限制,但直接使用模拟退火算法得到的Cs/Cv值与国家规范推荐值差距较大,物理意义有待商榷[1]。针对退火算法Cs/Cv值偏大问题,参考玛纳斯河上游肯斯瓦特水文站、煤窑水文站及附近水文站实测水文资料资料确定Cs/Cv值的变化范围为[2.5,4.5],以此为约束条件,构建离差绝对值和(ABS)最小的目标函数,采用模拟退火算法对混合分布进行参数估计。

模拟退火算法是一种拟合非线性函数的模型,适用于求解组合问题的全局最优解问题[16],计算策略如下:

a. 采用矩法初估参数,给定初始解ω,计算目标函数f(ω)。

b. 扰动产生新解ω′,计算目标函数f(ω′)。

c. 依据Metropolis准则计算Δf=f(ω′)-f(ω),若Δf≤0则接受f(ω′)作为新的当前解f(ω),否则以概率exp(-Δω/ω)接受f(ω′)作为新的当前解f(ω)。

d. 缓慢降低温度重置迭代数次,求解最优解。

2 玛纳斯河分析

玛纳斯河流域处于天山北坡、准噶尔盆地南部。地理位置于东经85°01′～86°32′,北纬43°27′～45°21′[7]。流域面积26 500 km2,地势东南高,西北低,地形坡降约为1/30～1/100,为内陆干旱区,具有显著大陆性气候,夏季炎热,冬季干冷,年均气温6.4°C,年降水量110～200 mm。玛纳斯河全长324 km,多年平均径流量12.53亿m3,是准噶尔盆地流量最大、流程最长的内陆河,属于暴雨型与融雪型混合补给的山溪性河流[8-9]。

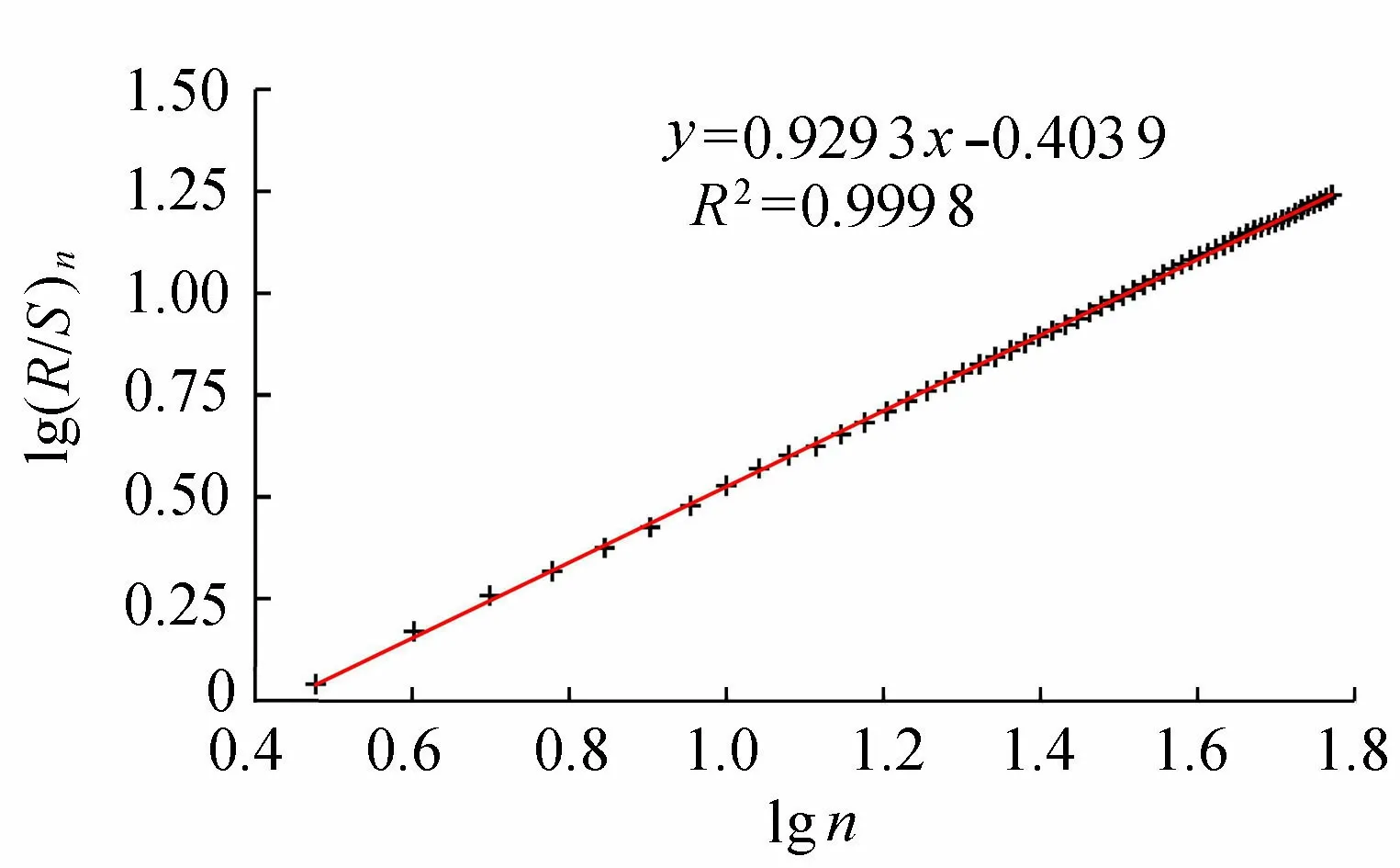
图1 玛纳斯河年径流R/S分析

2.1 年径流时间序列变异程度分析

对玛纳斯河1956—2014年年径流序列进行R/S分析,结果如图1所示。若系统独立同分布,则H=0.5。由图1可知,H=0.929 3,表明玛纳斯河年径流序列数据点范围超过了随机过程可能覆盖的范围,序列间各点必定是相互影响的,根据Hurst指数变异程度分级表(见表1)判断出玛纳斯河年径流序列存在巨变异。传统水文频率分析一致性假定显然与实际情况不符,需要进一步确定其具体变异年份。

表1 Hurst指数的变异程度分级[17]

2.2 年径流序列变化趋势及变异分析

2.2.1 滑动t检验

利用滑动t检验对玛纳斯河1956—2014年年径流序列进行趋势检验,结果如图2所示。取步长n1=n2=5,给定显著性水平α=0.05,t0.05=±2.306,自由度v=8。由图2可知,1956—2014年间有两次t检验统计值超过显著性水平,表明年径流序列发生两次显著突变, 1994—1999年年径流由多变少，而2002—2004年年径流又由少变多。虽然2000—2002年年径流增多,2004—2008年年径流减少,但均未达到显著性水平。1995年年径流检验统计值t最小(t=-4.082),因此1995年为年径流序列突变年份。

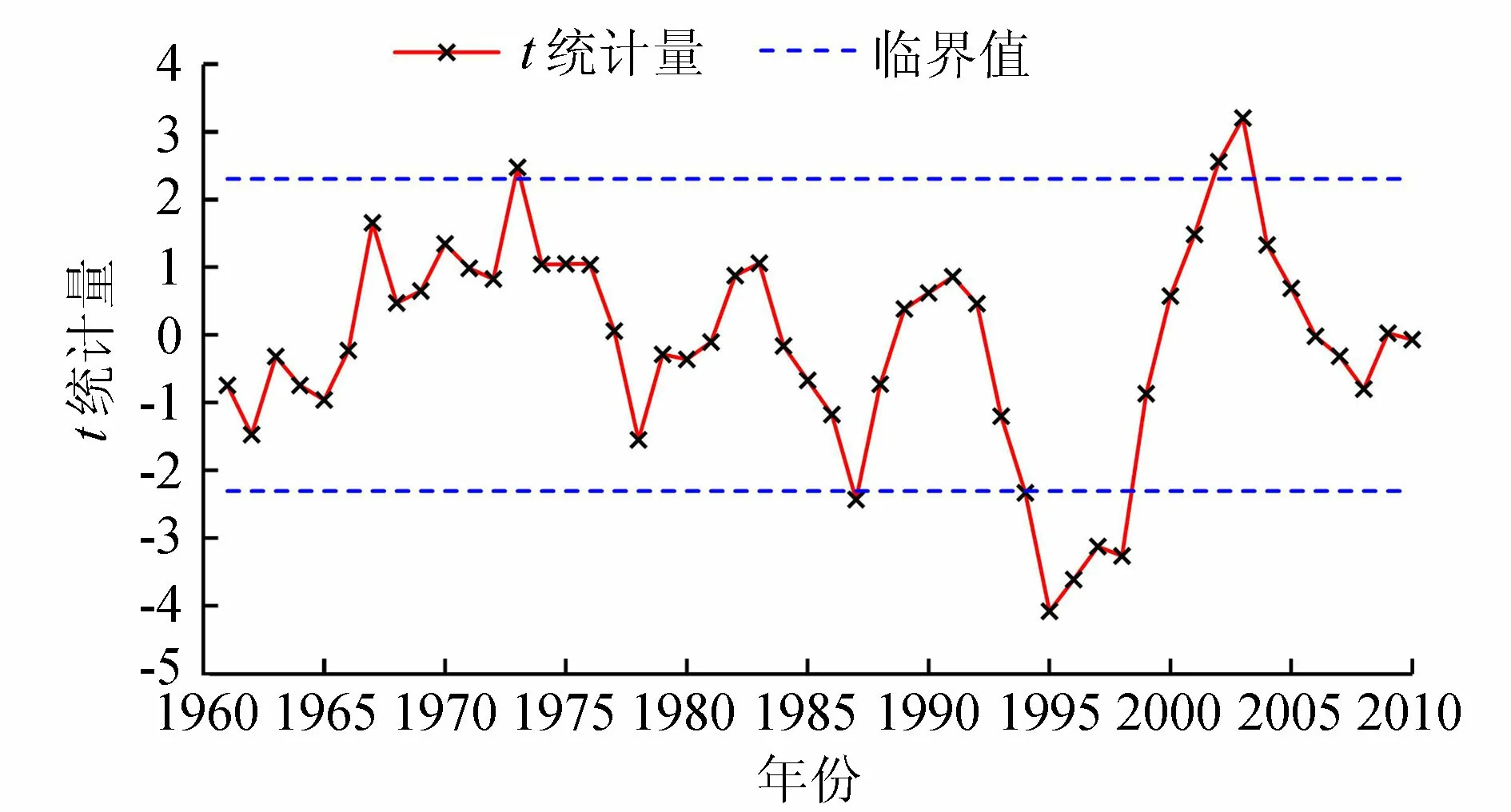
图2 玛纳斯河年径流滑动t检验曲线

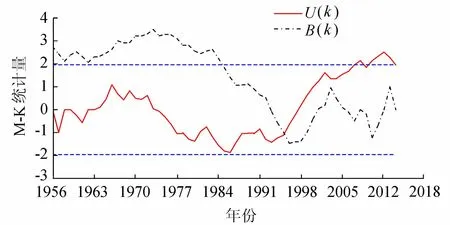
图3 玛纳斯河年径流Mann-Kendall检验

2.2.2Mann-Kendall检验

利用Mann-Kendall检验对玛纳斯河1956—2014年年径流序列进行趋势分析,结果如图3所示。由图3可知,Uk曲线在显著性水平为0.05情况下,1956—2003年年径流呈不规则的周期波动,变化趋势未达到显著水平;而2003—2012年,年径流有明显的增长趋势,尤其在2007—2012年,超过95%置信水平(u0.05=±1.96),表明年径流的增长趋势是显著的。根据Uk和Bk曲线交点位置确定其突变年份是1995年,这与滑动t检验结论相一致。

2.3 年径流序列模型对比分析

2.3.1 参数估计

对混合分布模型以ABS为目标函数,根据玛纳斯河上游肯斯瓦特水文站、煤窑水文站及附近水文站实测水文资料资料确定Cs/Cv值的变化范围为[2.5,4.5],以此条件为约束,采用模拟退火算法进行参数估计,而条件概率分布、P-Ⅲ分布以WLS为目标函数进行无偏估计。其结果见表2、表3。

表2 混合分布参数估计结果

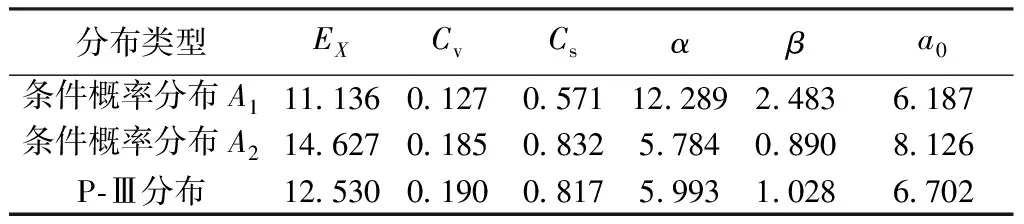
表3 条件概率分布及P-Ⅲ分布参数估计结果

表4 玛纳斯河设计年径流成果比较 亿m3

由表2、表3可知,混合分布模型与条件概率分布模型变异年份前后的年径流序列均值分别增加了23.98%和31.35%,变差系数分别增加了65.68%和45.67%,偏态系数分别增加了64.95%和65.71%。由于环境变化导致年径流序列变异年份前后参数变化显著,导致传统年径流频率分析方法的一致性假设不再满足。因此,对玛纳斯河年径流频率分析进行非一致性考虑更加符合实际情况。

2.3.2 年径流时间序列各分布拟合

对于条件概率分布模型,式(14)中变异点将年径流序列(n=59)划分为1995年以前(n1=40)序列A1和1980年以后(n2=19)序列A2,即s=2,P(A1)=40/59,P(A2)=19/59。混合分布模型由参数估计结果,按式(19)计算年径流序列混合分布理论频率。玛纳斯河年径流序列的不同分布拟合曲线如图4所示,设计年径流成果比较见表4。

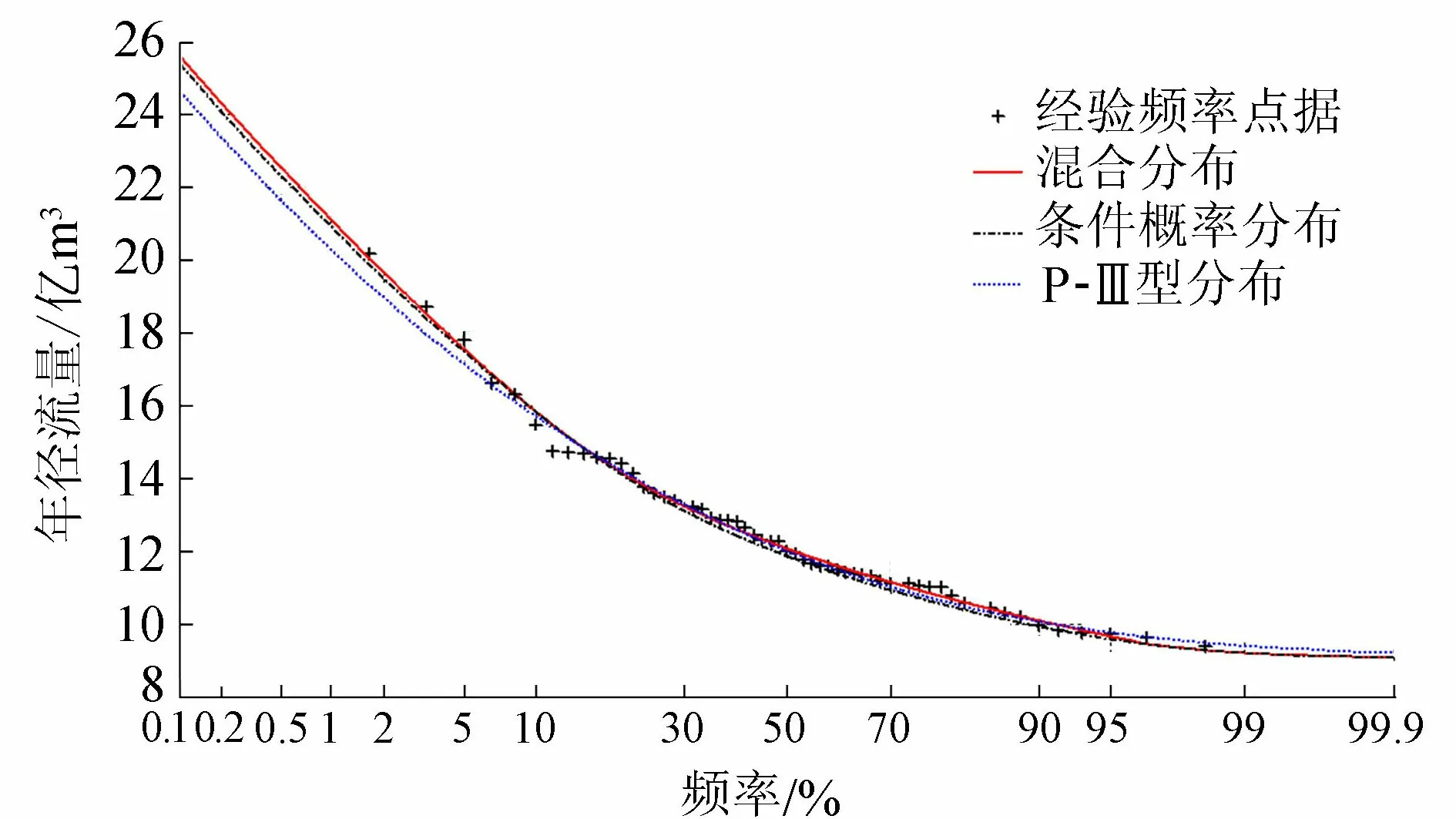
图4 玛纳斯河年径流时间序列分布拟合

由图4可知,拟合曲线上部混合分布和条件概率分布相近,与P-Ⅲ分布存在较大差异;拟合曲线中部混合分布拟合曲线有更大概率通过年径流实测值,拟合效果更佳;拟合曲线下尾段3种模型与经验点据拟合度高且无明显波动,拟合较好。由于混合分布模型和条件概率分布模型考虑了年径流序列的非一致性,采用两条不同参数的P-Ⅲ型曲线进行拟合,比传统P-Ⅲ型分布拟合曲线与经验点据拟合效果更佳。

由表4可知,3种模型在不同设计标准情况下,年径流设计值存在较大差异。当设计标准为50～5000年一遇条件下,混合分布模型设计成果与传统P-Ⅲ分布模型对比变化范围为3.29%～4.07%,而在相同设计标准情况下,混合分布模型与条件概率分布模型变化比例最大仅为0.95%,表明混合分布和条件概率分布考虑年径流的非一致性,所以设计值相近,但由于模型构建原理不同,故设计结果存在细微差异。现行规范采取一致性P-Ⅲ分布模型进行设计年径流计算与考虑非一致性模型相比差异较大,存在一定的设计风险。

2.3.3 模型拟合检验与拟合优度比较

对于玛纳斯河1956—2014年年径流序列分布的拟合进行拟合检验并对不同拟合分布进行拟合优度比较。采用Kolmogorov-Smirnov法检验观测的时间序列经验分布是否服从混合分布模型、条件概率分布模型,并对其拟合优度进行比较评价。构造柯尔莫哥洛夫统计量Dn为

(15)

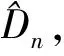
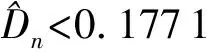
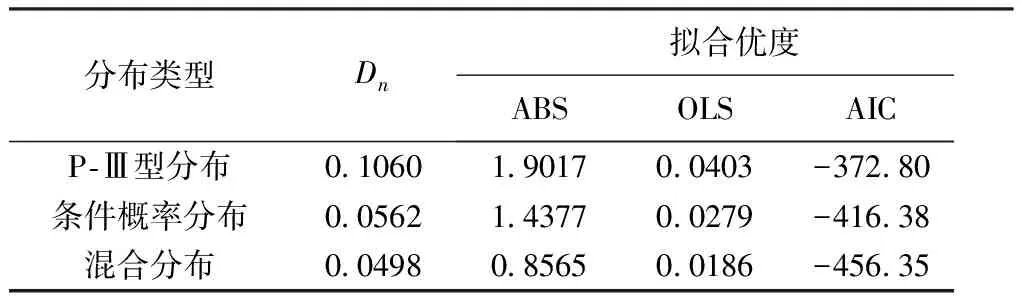
表5 玛纳斯河年径流序列分布拟合检验及拟合优度

由表5可知, P-Ⅲ分布、条件概率分布和混合分布对应的柯尔莫哥洛夫统计值分别为0.106 0、0.056 2和0.049 8,均小于临界统计值0.177 1,通过拟合检验。根据ABS、OLS、AIC拟合优度结果,混合分布模型各项拟合优度评价值分别为0.856 5、0.018 6和-456.35,均为三类模型最优值,故玛纳斯河年径流序列的最优分布模型为混合分布模型。

3 结 论

a. 玛纳斯河1956—2014年年径流序列的Hurst指数为0.929 3,存在巨变异。1995年为玛纳斯河年径流序列变异年份。

b. 混合分布模型的拟合曲线上部和条件概率分布相近,与P-Ⅲ分布存在较大差异;混合分布模型的拟合曲线中部比条件概率分布和P-Ⅲ分布拟合效果更佳;拟合曲线下尾段三种模型拟合度高且无明显波动,拟合较好。混合分布模型比P-Ⅲ型分布模型、条件概率分布模型拟合优度更佳,更适于对玛纳斯河年径流进行频率分析。

c.混合分布与传统P-Ⅲ分布设计年径流成果差异显著,表明依照现行的P-Ⅲ分布对玛纳斯河水资源进行规划设计会存在较大安全隐患。因此,为了提高玛纳斯河水资源利用可靠性和管理的科学性,有必要考虑年径流非一致性的最优分布模型——混合分布模型对现行玛纳斯河设计年径流进行修订。

[ 1 ] 梁忠民,胡义明,王军.非一致性水文频率分析的研究进展[J].水科学进展,2011,22(6):864-871.(LIANG Zhongmin,HU Yiming,WANG Jun.Advances in hydrological frequency analysis of non-stationary time series[J].Advances in Water Sciences,2011,22(6):864-871.(in Chinese))

[ 2 ] SINGH V P,WANG S X,ZHANG I.Frequency analysis of non-identically distributed hydrologic flood data[J].Journal of Hydrology,2005,307:175-195.

[ 3 ] SINGH K P,SINCLAIR R A.Two-distribution method for flood frequency analysis[J].Journal of Hydraulics Division,1972,98 (1):29-44.

[ 4 ] ALILA Y,MTIRAOUI A.Implications of heterogeneous flood-frequency distributions on traditional stream discharge prediction techniques[J].Hydrological Processes,2002,16(5): 1065-1084.

[ 5 ] 宋松柏,李扬,蔡明科.具有跳跃变异的非一致分布水文序列频率分析方法[J].水利学报,2012,43(6):734-739,748.(SONG Songbai,LI Yang,CAI Mingke.Methods of frequency analysis for hydrologic data with jump up components[J].Journal of Hydraulic Engineering,2012,43 (6):734-739,748.(in Chinese))

[ 6 ] 陈伏龙,王怡璇,吴泽斌,等.气候变化和人类活动对干旱区内陆河径流量的影响:以新疆玛纳斯河流域肯斯瓦特水文站为例[J].干旱区研究,2015,32(4):692-697.(CHEN Fulong,WANG Yixuan,WU Zebin,et al.Impacts of climate change and human activities on runoff of continental river in arid areas:taking Kensiwate Hydrological Station in Xinjiang Manas River Basin as an example[J].Arid Zone Research,2015,32(4):692-697.(in Chinese))

[ 7 ] 常浩娟,刘卫国,吴琼.60年玛纳斯河红山嘴径流规律特征分析[J].水土保持研究,2016,23(6):128-134.(CHANG Haojuan,LIU Weiguo,WU Qiong.Runoff characteristics of Hongshanzui Hydrologic Station of Manas River in the past 60 years[J].Research of Soil and Water Conservation,2016,23(6):128-134.(in Chinese))

[ 8 ] 沈雪峰,艾成.新疆玛纳斯河径流时间变化特征及其趋势分析[J].干旱区资源与环境,2012,26(7): 14-19.(SHEN Xuefeng,AI Cheng.Runoff change characteristics and the trend for Manasi River in Xinjiang[J].Journal of Arid Land Resources and Environment,2012,26(7):14-19.(in Chinese))

[ 9 ] 王文明,王文科,程旭光.玛纳斯河流域地下水库调蓄能力研究[J].水资源保护,2010,26(1):32-35.(WANG Wenming,WANG Wenke,CHENG Xuguang.Study on storage capacity of underground reservoir in Manasi River Basin[J].Water Resources Protection,2010,26(1):32-35.(in Chinese))

[10] 邱海军,曹明明,胡胜,等.近60 a来中国洪涝灾情变化趋势持续性和周期性研究[J].地球与环境,2014,42(1):17-24.(QIU Haijun,CAO Mingming,HU Sheng.Susceptibility and periodicity of flood disasters since the 1950 s in China[J].Earth and Environment,2014,42(1):17-24.(in Chinese))

[11] 李子远,冯平,苑希民.黄河宁夏段干支流非一致性洪峰遭遇风险分析[J].水利水电科技进展,2016,36(6):51-57.(LI Ziyuan,FENG Ping,YUAN Ximin.Coincidence risk analysis for non-stationary flood peak of Yellow River and its tributaries in Ningxia Hui Autonomous Region[J].Advances in Science and Technology of Water Sciences,2016,36(6):51-57.(in Chinese))

[12] KRISHAN P.SINGH.A versatile flood frequency methodology[J].Water International,1987,12(3):139-145.

[13] ROSSI F.Two-component extreme value distribution for flood frequency analysis[J].Water Resources Research,1984,20(7): 847-856.

[14] FIORENTINO M,ARORA K,SINGH V P.The two-component extreme value distribution for flood frequency analysis: derivation of a new estimation method[J].Stochastic Environmental Research and Risk Assessment,1987,1 (3): 199-208.

[15] 成静清,宋松柏.基于混合分布非一致性年径流序列频率参数的计算[J].西北农林科技大学学报(自然科学版),2010,38(2): 229-234.(CHENG Jingqing,SONG Songbai.Calculation of hydrological frequency parameters of inconsistent annual runoff series based on mixed distribution[J].Journal of Northwest A&F University(Nature Science Edition),2010,38(2): 229-234.(in Chinese))

[16] 陈子燊,刘曾美,路剑飞.广义极值分布参数估计方法的对比分析[J].中山大学学报(自然科学版),2010,49(6): 105-109.(CHEN Zishen,LIU Zengmei,LU Jianfei.Comparative analysis of parameter estimation methods of generalized extreme value distribution[J].Acta Scientiarum Maturalium Universitatis Sunyatseni(Nature Science),2010,49(6): 105-109.(in Chinese))

[17] 谢平,陈广才,雷红富,等.水文变异诊断系统[J].水力发电学报,2010,29(1): 85-91.(XIE Ping,CHEN Guangcai,LEI Hongfu,et al.Hydrological alteration diagnosis system[J].Journal of Hydroelectric Engineering,2010,29(1): 85-91.(in Chinese))