扁平管袋裸坝基于波浪作用的稳定性公式推求

林 刚,束一鸣,毛文龙

(1.山东省烟台市水利局,山东 烟台 264009; 2.河海大学水利水电学院,江苏 南京 210098)

土工织物充填管袋是用泥砂等混合液体材料充入土工织物管袋中,待管袋逐渐脱水固结具有一定承载力后,可作为修建河口水库堤坝、深水航道导流堤、沿海港口码头、沿海机场、沿海堤防及围垦匡围堤防等基础设施的重要构筑物[1-2]。自20世纪50年代荷兰三角洲工程(Delta Project)率先运用充填管袋以来,因其具有经济、环保等优点,愈来愈广泛应用于土木、水利等工程建设领域,发挥了重要作用[3-5]。我国自20世纪80年代引入管袋筑坝技术,目前已广泛应用于东部沿海、沿江河口等地区[6-8]。

在施工过程中,坝体结构外侧尚未进行防护的管袋坝称为管袋裸坝。在国外土工管袋技术广泛应用的同时,科研人员还重视对管袋结构稳定性理论研究,至今已取得丰硕成果[9-11]。近年来我国研究人员对国内广泛采用的扁平管袋结构受波浪冲击下的稳定性问题展开了持续不断的研究,分析了管袋堤坝不同结构形式在不同波高、波陡、水深等波浪环境作用下的稳定性[12-15]。但有关波浪作用下管袋结构稳定基础性理论仍不成熟,有关管袋在波浪作用下变形引起受力变化及相应的结构稳定等基础性问题探究不多,因此有必要对波浪作用下扁平管袋裸坝结构受力、变形及其稳定性理论公式建立等问题进行深入探讨。

1 扁平管袋结构稳定性公式

1.1 管袋结构受力分析

目前国内使用的扁平管袋坝体结构大多体积较大,属于大尺度结构,可采用大尺度结构波浪载荷分析方法——奇点分布法来分析扁平管袋裸坝结构表面所受波浪点压力。对每一层扁平管袋而言,管袋层的高度相对于整体结构尺度较小,在同一层管袋内管袋表面所承受的压力可近似看作常量,即同一管袋层不同点所受到同一方向的力大小相同。在求得结构表面点压力的基础上,分别将各层管袋沿着平行于水流和垂直于水流的方向进行投影,则垂直于水流方向的管袋弧形面积可转换为矩形面积,平行于水流方向的管袋面积即为底部表面积,而作用在迎浪面管袋平面上的点压力就可通过积分求得管袋各个面所承受的合力。由此,可进一步分析作用在管袋结构上的波浪力。

如图1所示,扁平管袋层(单个)可看作4个面的封闭图形,由面s1、s2、s3、s4围成,扁平管袋所受水平波浪力Fh为4个面所受水平力之和:

(1)

式中:ni为管袋各个面的单位法向量;Fi为波浪作用于管袋各个面的点压力,即均布作用力。

图1 管袋层法向受力示意图(横剖面)

由图1可以看出,管袋层上、下两面所受波浪力水平方向分量为零,因此式(1)中第2、3项为零。管袋背水面认为无波浪作用,因而该式第4项积分为零。设扁平管袋长度(顺波浪传播方向)、宽度(垂直波浪方向)和高度分别为alt、lt和blt,其中a、b为管袋尺寸组合系数,则式(1)可简化为

(2)

式中:F为管袋裸坝结构表面所受波浪点压力;As为垂直于水流方向的管袋投影面积。

同理,得到扁平管袋所受上抬力Fl和管袋重力Fg分别为

(3)

(4)

式中:At为平行于水流方向的管袋投影面积;ρs为充填物密度;ρ为(海)水的密度;g为重力加速度;V为充填扁平管袋的体积。

管袋结构滑动时的受力如图2所示。

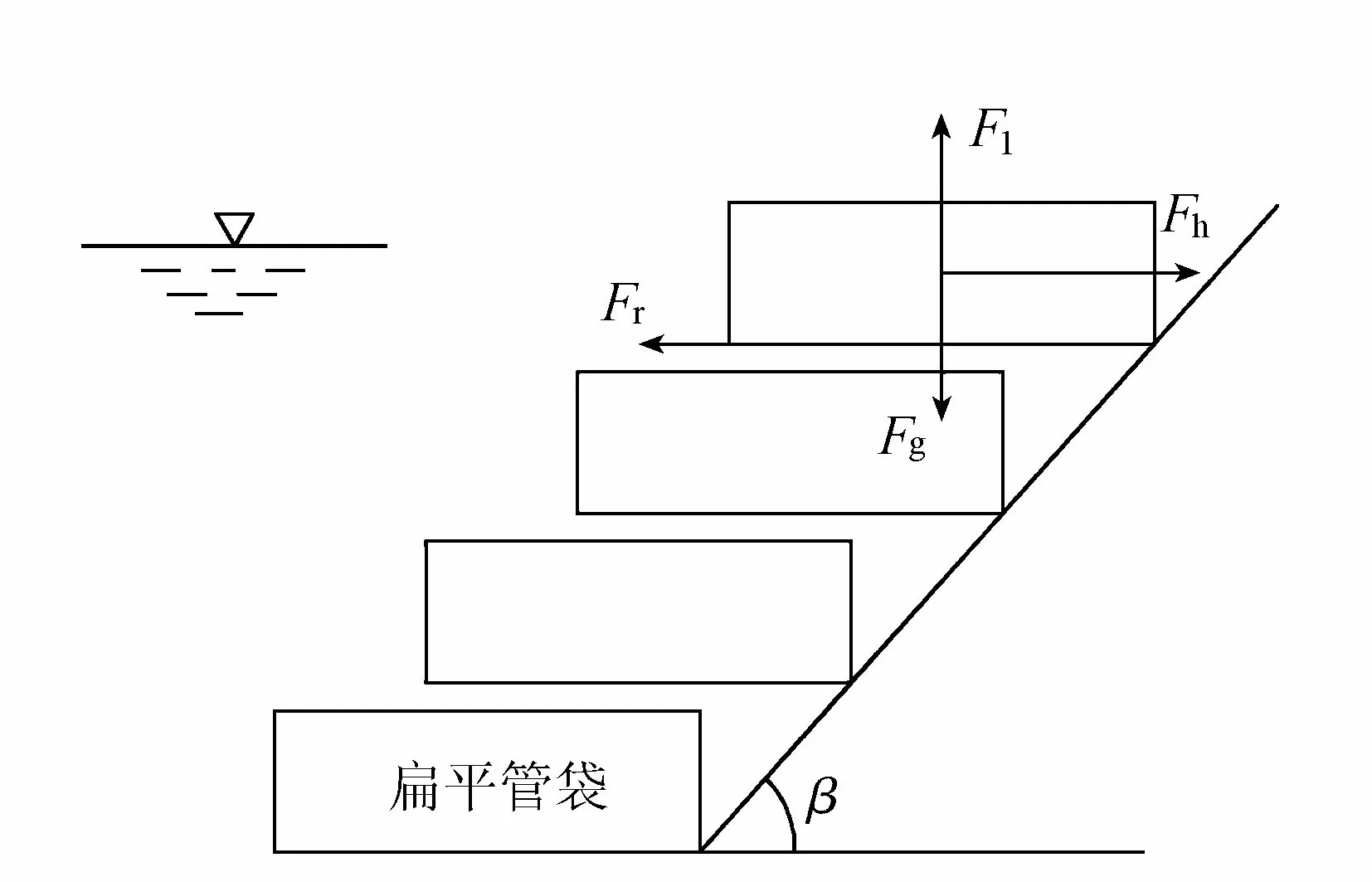
图2 管袋结构滑动时所受波浪力示意图

1.2 稳定性公式

扁平管袋结构失稳有两种方式:一种是管袋产生水平位移,结构不能保持整体性的滑动失稳破坏;另一种是管袋被掀翻,结构产生倾覆失稳破坏。

1.2.1 滑动失稳

当管袋发生滑动位移时,根据力平衡原理,要使管袋保持稳定,则必有抵抗力大于或等于管袋所受水平波浪力,即

Fr=μ(Fg-Fl)≥Fh

(5)

式中:Fr为管袋抵抗力;μ为土工织物管袋之间的摩擦因数。

联合求解式(2)～(5)即可得到为使管袋保持稳定,管袋的长度lt1为

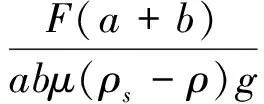
(6)

考虑管袋充填后,联合求解(4)(6),其重力Fg1须满足

(7)

1.2.2 倾覆失稳

假定管袋的倾覆力矩作用点位于管袋尾部,当作用在管袋上的倾覆力矩大于其抵抗力矩时,管袋发生倾覆失稳。由此,为使管袋保持稳定,需满足:

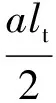
(8)

相应地,要使管袋结构保持稳定,所需的管袋长度lt2为

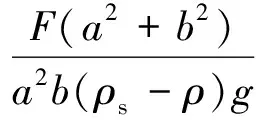
(9)

进而可得到使管袋结构保持稳定时,所需的管袋重力Fg2为

(10)

1.2.3 考虑结构变形的稳定性公式

因管袋变形改变波浪力作用在管袋上的受力面积,必然对管袋稳定产生影响。为使推导出的管袋稳定性公式具有普遍适用性,引入管袋变形因子来考虑管袋变形对结构稳定性的影响。在式(6)(7)(9)和(10)中加入变形因子,分别得到考虑管袋变形情况下的管袋裸坝结构滑动失稳和倾覆失稳稳定性公式:

(11)

(12)

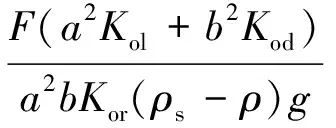
(13)

(14)

式中:Kd、Kl、Kr分别为管袋产生滑动位移时作用在管袋上的水平力、上抬力及管袋抵抗力变形因子;Kod、Kol、Kor分别为管袋产生倾覆位移时作用在管袋上的水平力、上抬力以及抵抗力的力矩变形因子。

1.3 公式应用

稳定性公式(11)～(14)应用时,须已知海洋环境波浪参数、土工织物管袋之间及管袋与海底基床土之间的摩擦因数(为简化,这里均采用摩擦因数μ表示)和管袋变形因子等参数。其中波浪参数可以通过合适的波浪理论来模拟计算,摩擦因数可通过剪切试验确定,管袋变形因子可通过模型试验数据计算获得,由此就可初步确定满足筑坝过程中裸坝结构稳定的管袋大小或重力。试算步骤如下:

第1步针对工程所处波浪水流环境,选取合适的波浪理论进行简化,运用大尺度结构波浪力分析方法,推算管袋裸坝结构表面所受波浪点压力F分布。

第2步从模型试验数据计算得到的管袋变形因子Kd、Kl、Kr、Kod、Kol、Kor中,选取一组初始值。

第3步设定管袋尺寸组合系数a和b。

第4步运用管袋结构稳定公式(11)～(14),计算出相应的管袋长度(lt1或lt2)和重力。

第5步采用第4步中计算得到的管袋长度lt1或lt2,分别计算管袋长、宽、高。如需进一步优化,则按第3、4、5步重新进行计算,直至得到符合工程实际的管袋尺寸和重力。

由于扁平管袋失稳方式包括滑动失稳和倾覆失稳,因此在计算过程中分别按滑动失稳和倾覆失稳情况,按第1～5步的顺序计算,最终选取计算的管袋尺寸较大值作为设计值。

综上可知,运用管袋结构稳定性公式计算管袋尺寸,需已知管袋变形因子,而管袋变形因子是通过管袋结构在波浪作用下的模型试验数据计算得来的。对此,下文通过对扁平管袋受波浪作用模型试验以及管袋变形因子分析来计算管袋变形因子。

2 管袋变形及稳定模型试验

2.1 试验模型

试验在河海大学海岸灾害及防护教育部重点实验室河口航道实验厅完成,利用二维不规则波浪水槽造波系统进行模拟波浪-结构模型试验。该系统由长80 m、宽80 cm、高120 cm的玻璃水槽与液压伺服系统和控制系统构成。水槽的一端设有造波机及控制系统,另一端设置有控制室和消力池。水槽试验段沿水流方向设有一块玻璃隔断,将80 cm宽度水槽分成两部分,其中试验部分宽50 cm(模型布置一侧),另一部分宽30 cm,其主要目的是为了减少波浪二次反射,更好地模拟波浪-管袋结构相互作用实际情况。

根据JTJ/T 234—2001《波浪模型试验规程》相似准则有关规定,采用正态模型,管袋模型与原型满足几何、运动和动力相似,同时由于管袋结构在波浪作用下重力占主导地位,还需满足重力相似准则。结合实际情况,试验模型比尺设为1∶30。为便于试验和分析,设计管袋模型宽度与水槽试验宽度相同(50 cm),迎浪面管袋模型长42 cm、高2 cm。考虑到扁平管袋筑坝技术发展迅速,管袋坝高度越来越高,为使试验成果具有一定的前瞻性,在设计管袋裸坝高程时考虑较高坝体,最终确定管袋裸坝模型高50 cm(即对应原型坝高15m)。结合上海青草沙工程和洋山港工程中裸坝坝顶宽度5～6 m,确定模型裸坝坝顶宽度18 cm(即对应原型5.4 m)。迎水坡坡率设为1∶1.5和1∶2.0,试验管袋编织布规格为150 g/m2,充填砂干密度为1.64 g/cm3。

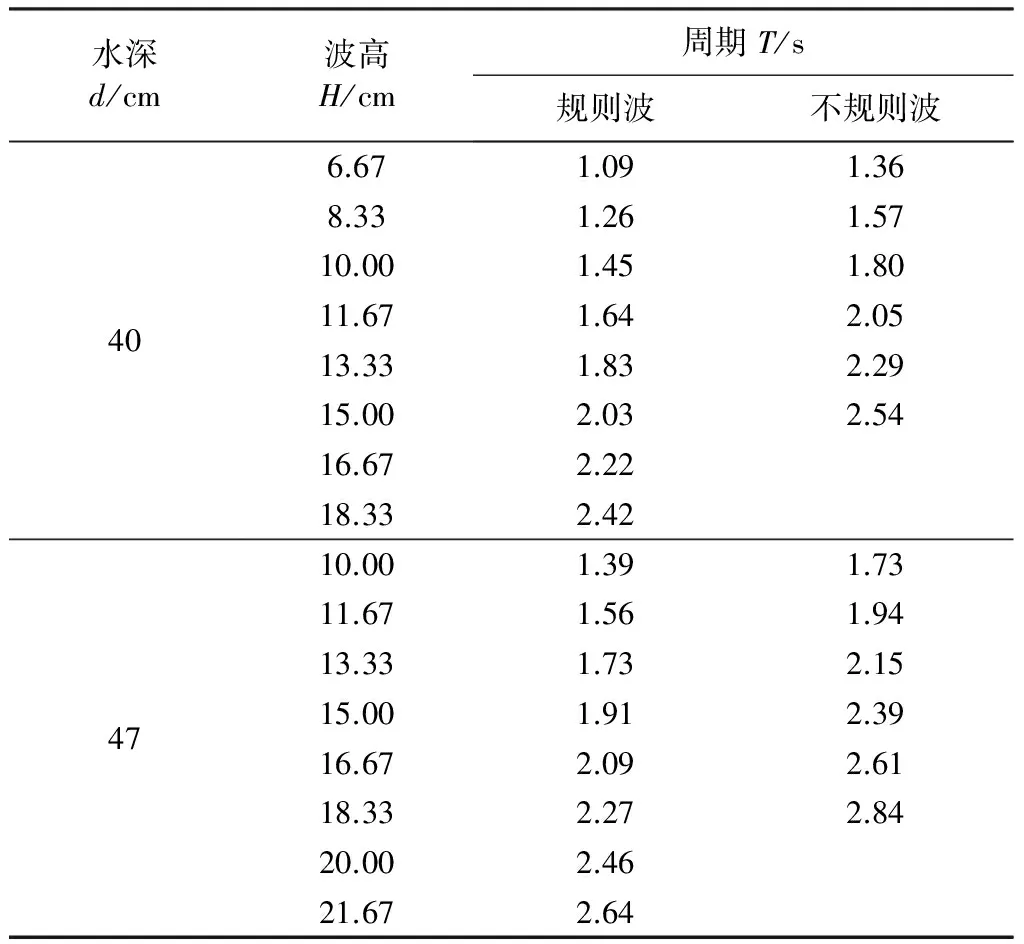
表1 试验波浪要素

试验采取规则波和不规则波两种波型,水深分别为40 cm和47 cm,波浪波陡H/L为1/25,波高介于6～22 cm之间。两种坡率工况下的波浪要素完全一致,如表1所示。设计了试验裸坝结构刚开始铺设一层管袋至按设计坝高全部铺设到位过程中多种结构模型,对每一种管袋裸坝结构模型,均按以下步骤进行试验:①向水槽注水，调节水槽控制系统伺服控制器生成满足试验条件的波浪；②开始试验、观察并记录管袋变形稳定情况；③按率定波浪要素依次试验直至结构失稳破坏。

2.2 试验现象

在较强波浪作用下,结构失稳破坏,管袋发生剧烈变形。结构失稳方式既有滑动失稳,又有倾覆失稳。例如,在水深40 cm、坡率1∶1.5、波高H=13.33 cm、周期T=1.83 s情况下,管袋结构破坏的具体表现形式为:顶层管袋很快被冲出坝体,接着第2层、第3层直至第6层管袋相继被冲出坝体,第6层以下到第13层管袋有剧烈变形发生。另外,当每层只布置一个管袋时,通常是发生滑动失稳破坏,而当同一层布置有2个及以上的管袋时,裸坝结构迎浪面斜坡管袋发生倾覆失稳的可能性更大。试验中一组扁平管袋结构模型变形前后对比如图3所示。

理论上讲,裸坝结构迎浪面管袋上抬角α介于0°～90°之间,对于上抬角超过90°的情况,管袋不能再恢复原状,不存在后续变形可能,故不予讨论。试验现象也证实了这一点,当上抬角接近或达到90°时,结构已发生倾覆失稳破坏。通常情况下,管袋上抬角介于0°～45°之间。经多次试验观测,除斜坡管袋位移并不明显时顶层管袋就开始失稳等少数情况外,多数情况当管袋上抬角超过35°时管袋就开始处于不太稳定状态,直至结构失稳破坏。为了量化管袋因上抬变形对结构稳定性的影响,本文选取管袋上抬角为35°进行计算,上抬部分管袋长度为15.12 cm。试验中,管袋裸坝结构上抬变形如图4所示。

图4 扁平管袋上抬变形示意图(α=35°)

3 变形因子分析

由于管袋上抬变形减少了与相邻下层管袋的接触面积,势必对管袋的稳定性产生不利影响。根据试验现象还可以知道:当管袋裸坝结构受波浪力作用出现上抬变形时,并不是所有迎浪面管袋均出现这种变形,通常的现象是最上面几层管袋上抬变形轻微或者不明显,而斜坡管袋出现上抬变形的现象较为常见,各迎浪面斜坡管袋的上抬变形一般并不一致。为了简化计算,本文假设裸坝结构迎浪面管袋均会发生上抬变形,且变形的形式趋于一致。

波浪作用下管袋变形对管袋结构的影响因素主要包括:管袋平行于水流传播方向的受力面积At和垂直于水流方向的投影面积As以及管袋重力Fg。其中,管袋上抬变形后管袋的受力面积As和At可以很容易求得;关于管袋重力,因管袋变形引起的抵抗力变化,在经过适当简化后也可推求。

3.1 滑动失稳

在管袋裸坝结构中,由于斜坡管袋和顶层管袋所受的波浪荷载及所处结构中位置的不同,导致其变形对结构稳定性的影响会有相应差异,本文分别探讨斜坡管袋和顶层管袋变形因子。

3.1.1 斜坡管袋

3.1.1.1 主动力变形因子

图5 管袋上抬变形受力面积变化

(15)

相应地,上抬力变形因子Kl为

(16)

计算表明,当α=35°时,扁平管袋变形后所受的水平力是未变形的5倍多(Kd=5.16),不利于结构的稳定;变形后所受的上抬力是未变形的0.93倍(Kl=0.93),有利于结构的稳定。

3.1.1.2 抵抗力变形因子Kr

Recio等[11]认为,管袋上抬变形发生后,管袋抵抗力受两方面因素影响:一是管袋与相邻管袋接触面积减少导致抵抗力降低,二是上层管袋提供有效重力而导致抵抗力增加。变形后,斜坡管袋的抵抗力由其上部呈三角形棱体形状管袋体的重力提供。

对比管袋变形前后的抵抗力,可得

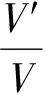
(17)

扁平管袋变形后的体积与管袋的形状有直接的关系。根据Recio等[11]的分析方法,管袋上抬变形部分的长度与管袋结构迎浪面上抬角有直接关系,即管袋上抬部分的长度等于实际管袋上抬长度与上抬角的正切之比,在本试验中,管袋上抬部分长度la为

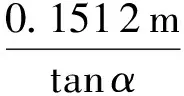
(18)

由此,斜坡管袋与其上一层相邻管袋沿波浪传播方向有效接触长度le为管袋长度alt与上抬部分长度la之差,即

le=alt-la=0.42 m-0.151 2 m×cotα(19)

变形后斜坡管袋提供抵抗力部分如图6所示。

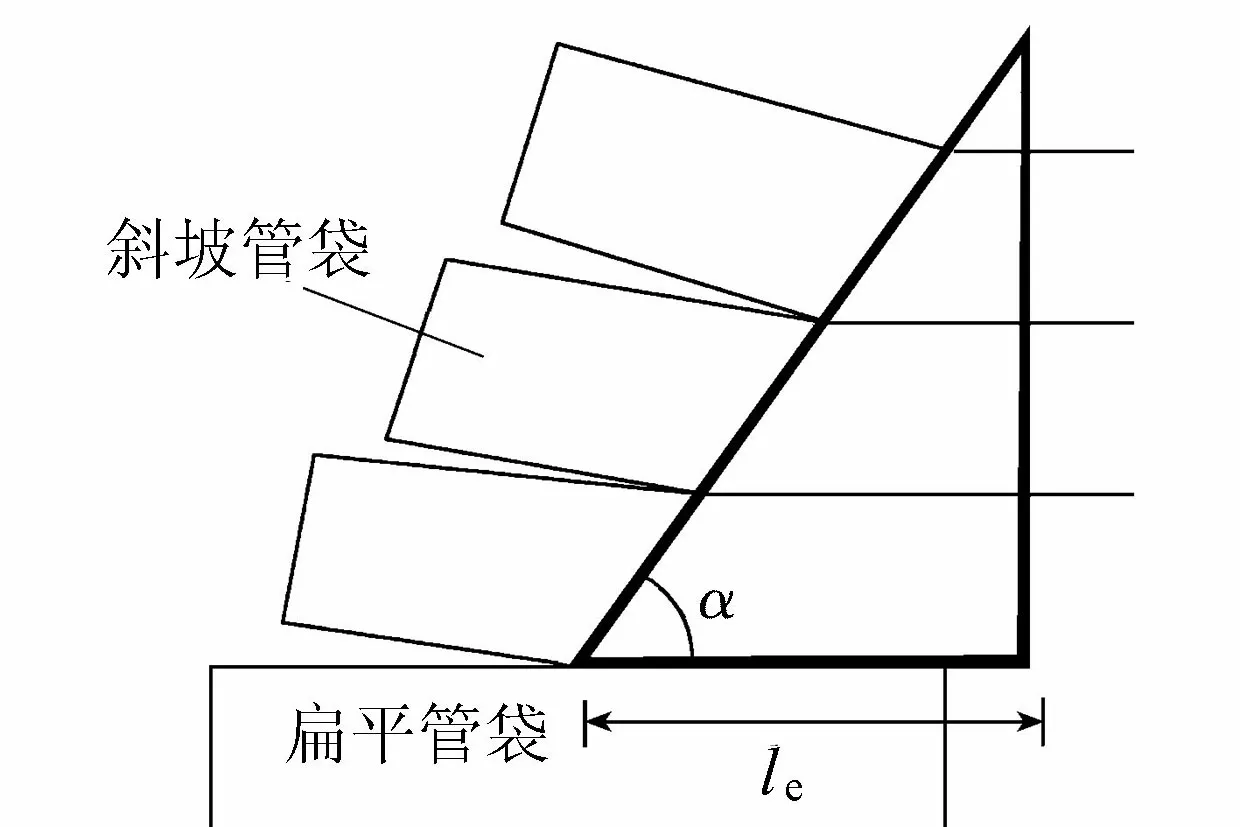
图6 变形后斜坡管袋提供抵抗力部分示意图

当上抬角α=35°时,由式(18)可计算得斜坡管袋抵抗力变形因子Kr=1.74,即变形后的抵抗力是未变形的1.74倍,有利于结构的稳定。

以上是在假设管袋上抬角α=35°时的抵抗力变形因子。同理,可以计算出上抬角为其他值时的斜坡管袋抵抗力变形因子,得到抵抗力变形因子与裸坝结构上抬角之间的函数关系如图7所示。可以看出,裸坝坝体上抬角越大,抵抗力变形因子越大,且增长幅度有变大的趋势。

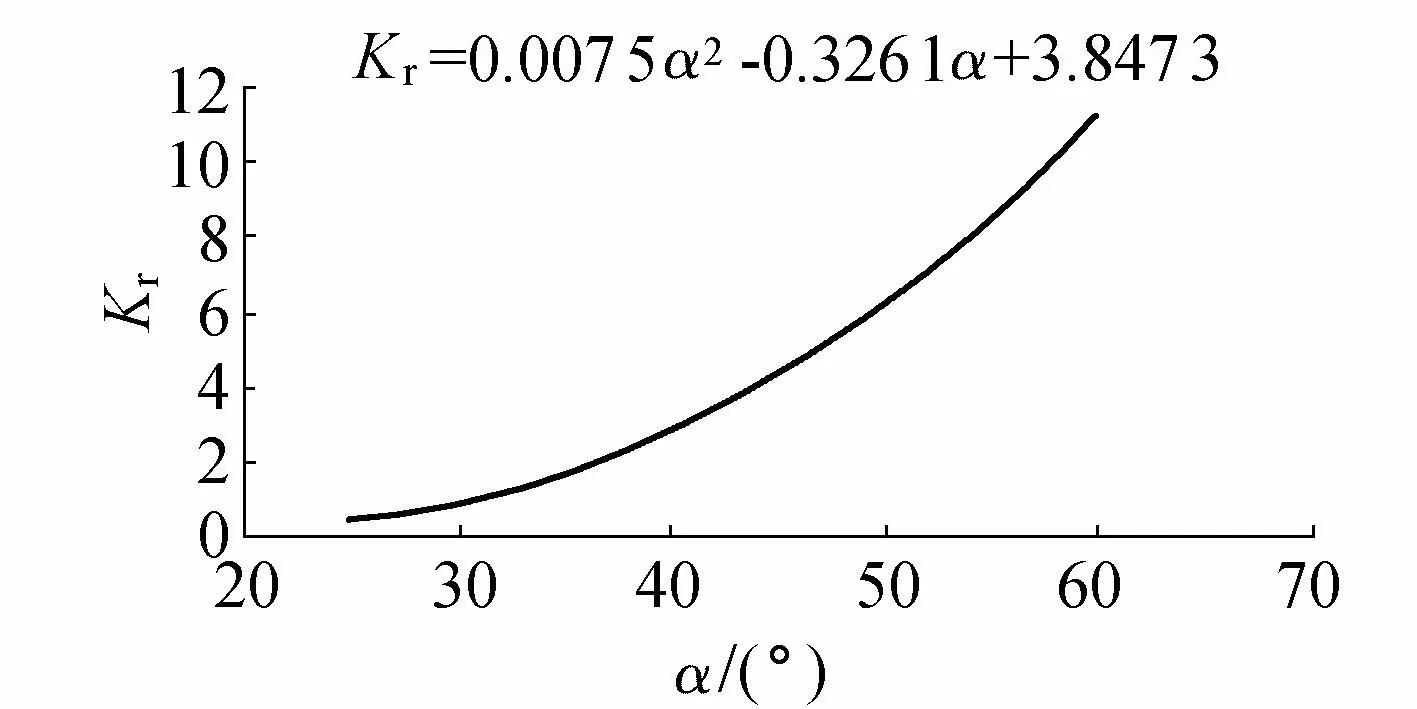
图7 斜坡管袋抵抗力变形因子与上抬角关系曲线

3.1.2 顶层管袋

基于本文假设斜坡管袋与顶层管袋的变形一致,故推求顶层管袋的水平力及上抬力变形因子方法与斜坡管袋一样,因此,顶层管袋的水平力及上抬力变形因子与斜坡管袋相同。

由于顶层管袋上面没有别的管袋,所以其与斜坡管袋处理方法的不同之处在于顶层管袋没有更上层管袋提供的有效重力。根据Recio等[11]采用的分析方法,认为顶层管袋变形后,抵抗失稳的管袋部分为梯形棱柱体,如图8所示。

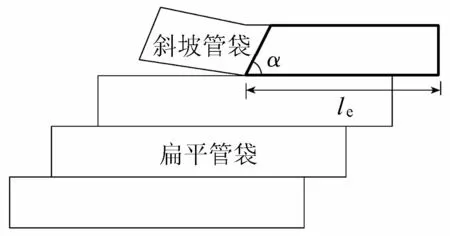
图8 顶层管袋变形后提供抵抗力部分示意图

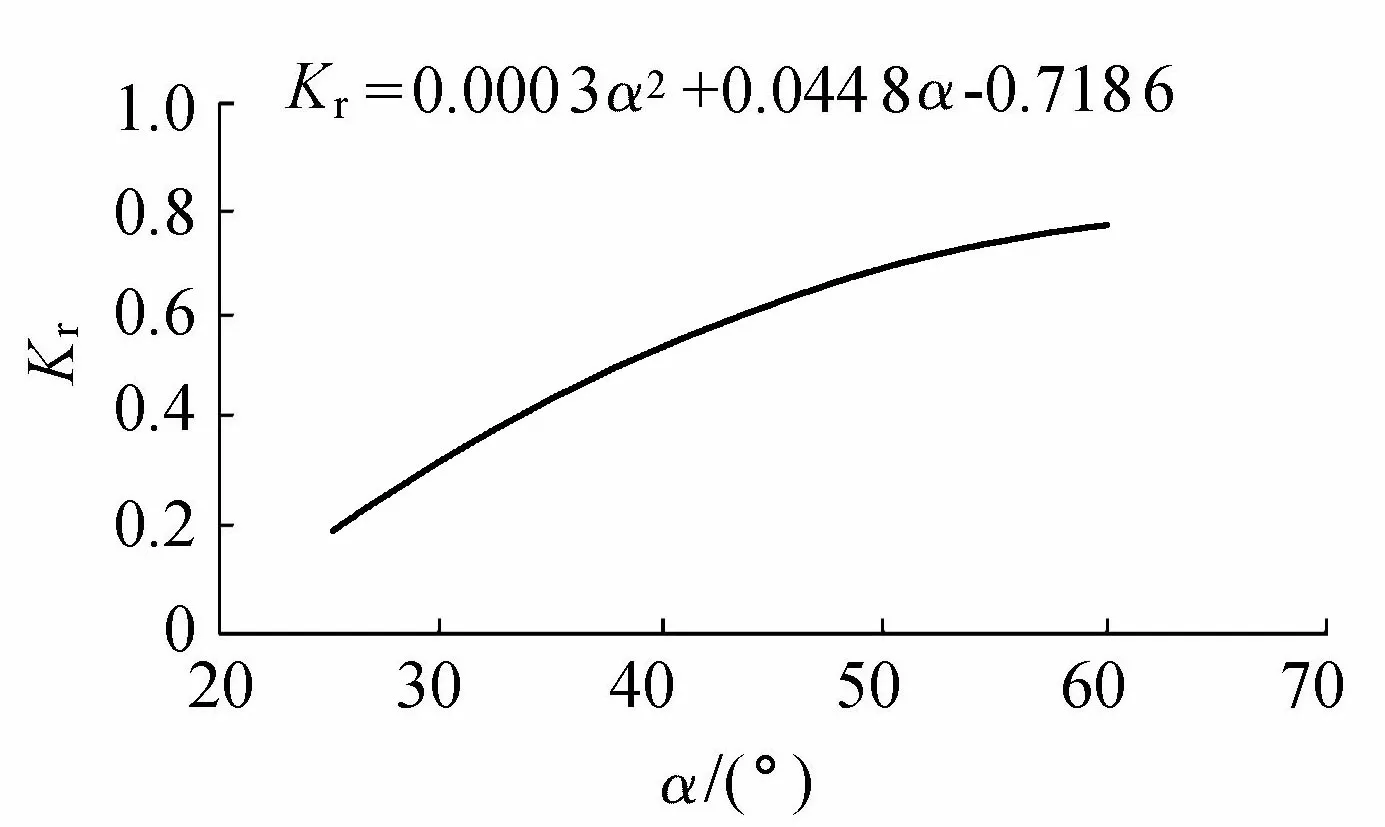
图9 顶层管袋抵抗力变形因子与上抬角关系曲线

当顶层管袋发生上抬变形后,在滑动位移瞬间,上抬部分不提供抵抗力,因此,上抬管袋变形后的重力计算即按图8所示梯形棱体来考虑。根据梯形棱体体积计算公式,可计算得到当α=35°时梯形棱体的体积为0.001 898 m3,根据式(17)可计算得到顶层管袋抵抗力变形因子Kr=0.45,即顶层管袋变形后的抵抗力对结构稳定性的影响,是未变形的0.45倍,不利于结构的稳定。相应地,可以计算出上抬角为其他值时的抵抗力变形因子,得到顶层管袋抵抗力变形因子与裸坝结构上抬角关系曲线如图9所示。可以看出,裸坝坝体上抬角越大,抵抗力变形因子越大,且增加幅度有变缓的趋势。

3.2 倾覆失稳

当扁平管袋发生上抬变形后,其重心也相应改变。为了推求管袋裸坝结构发生倾覆失稳情况下管袋变形对结构稳定性的影响,首先应确定变形后管袋的重心位置,分析变形后管袋受力对倾覆失稳点的力矩。经计算,变形后管袋的重心已不在其形状内部,而是在其外部。变形后的重心到管袋尾部下沿的水平距离为0.201 6 m,垂直距离为0.025 4 m。

根据试验现象可知,管袋裸坝结构发生倾覆失稳的管袋通常是结构的顶层管袋(当顶层管袋被冲出坝体后,新的顶层管袋成为最可能发生倾覆失稳的管袋,依次类推)。故以下只分析顶层管袋倾覆失稳情况下的管袋变形因子。

分析顶层管袋倾覆失稳变形因子主要考虑两方面因素:一是管袋变形前后受力的变化;二是由于变形后管袋的重心发生改变,相应的管袋作用力矩发生变化。管袋变形前后管袋受力、重心及倾覆点如图10所示。

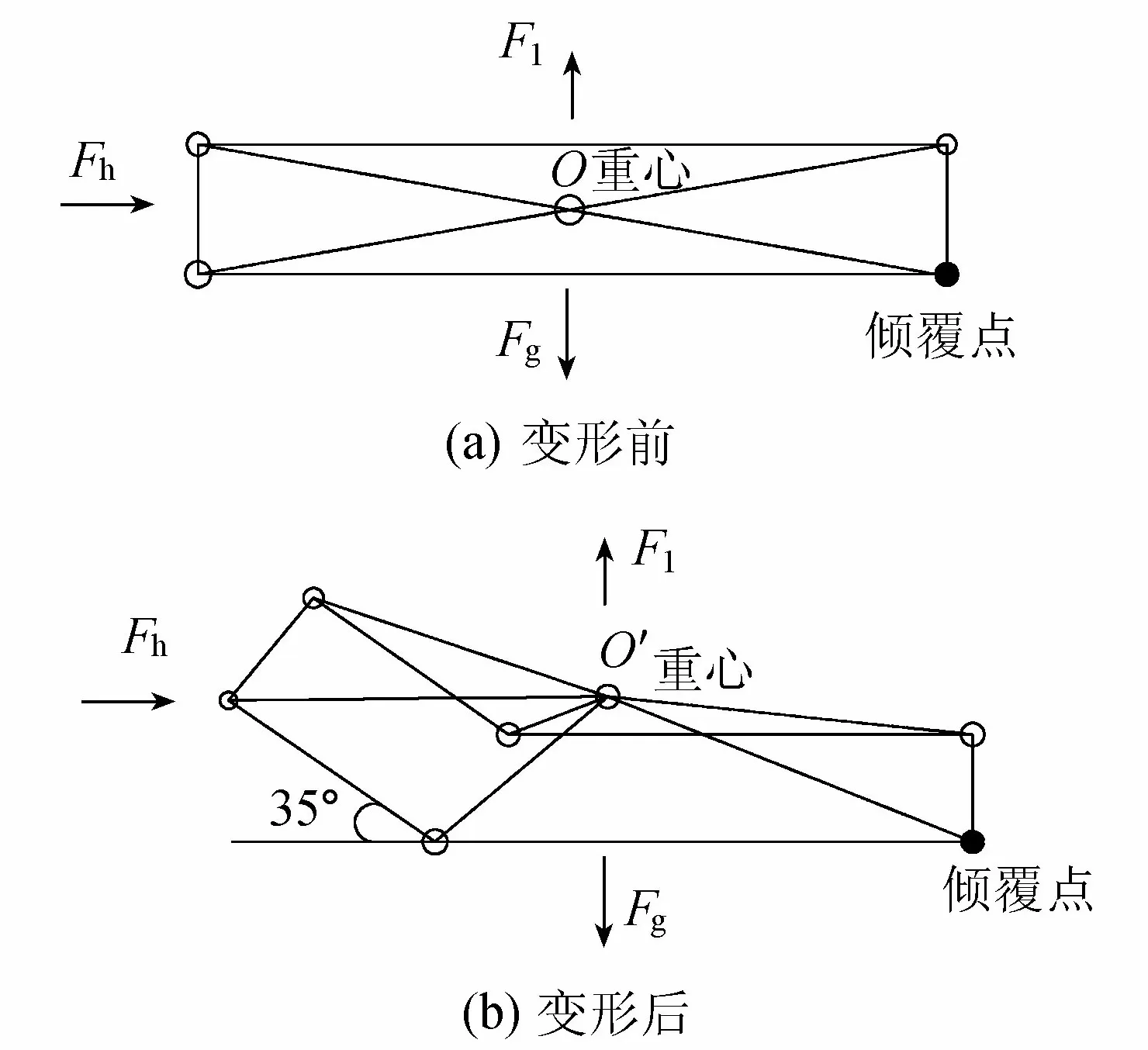
图10 顶层管袋变形前后管袋受力、重心及倾覆点示意图

a. 主动力力矩变形因子。管袋变形不但影响管袋所受水平力作用面积As,同时影响管袋重心与倾覆点之间的垂直距离,因此,倾覆失稳时顶层管袋水平力力矩变形因子Kod可表示为

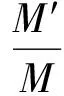
(20)

式中:M、M′ 分别为变形前后水平力力矩;m、m′分别为变形前后管袋的水平力力臂,即管袋重心与管袋倾覆点之间的垂直距离。相应地,可得上抬力力矩变形因子Kol为

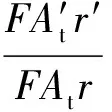
(21)

式中r、r′分别为变形前后管袋的垂直力力臂,即管袋重心与管袋倾覆点之间的水平距离。计算结果表明,当α=35°时,变形后的水平力力矩对管袋结构稳定性的影响,是未变形的13倍多(Kod=13.11),不利于结构的稳定;变形后的上抬力力矩对管袋结构稳定性的影响,是未变形的0.9倍(Kol=0.90),有利于结构的稳定。

b. 抵抗力力矩变形因子Kor。应注意的是,当分析管袋滑动失稳时,管袋上抬部分对管袋稳定性不提供抵抗力;而分析管袋倾覆失稳时,管袋充填物重力对管袋稳定性提供抵抗力。因此,管袋变形后,抵抗力力矩只考虑因重心变化引起的抵抗力作用力臂的改变,故结合管袋重心改变量，倾覆失稳时顶层管袋抵抗力力矩变形因子Kor=r′/r=0.96(α=35°),即变形对管袋结构稳定性的影响是未变形的0.96倍,不利于结构的稳定。

4 结 语

运用大尺度结构波浪载荷分析方法——奇点分布法分析了扁平管袋裸坝结构表面波浪力分布,根据力和力矩平衡原理,分别推导出管袋裸坝结构在波浪水流作用下滑动失稳和倾覆失稳稳定性公式。然后考虑变形对滑动失稳管袋所受波浪力和自重力及倾覆失稳相应力矩的影响,通过引入管袋变形因子,建立了管袋变形情况下的稳定性公式。

在稳定性公式的基础上开展多工况扁平管袋裸坝结构稳定模型试验,得到了管袋失稳方式和相应的变形参数。管袋裸坝失稳主要是滑动失稳和倾覆失稳,失稳方式与管袋所处位置相关。对于顶层管袋,既能发生倾覆失稳,又能发生滑动失稳;而斜坡管袋只能发生滑动失稳。经多次试验观测,管袋变形上抬角为35°,上抬部分管袋长度为15.12 cm。

结合模型试验结果对引入变形因子的稳定性公式进行定量分析,分别探讨了管袋变形对裸坝发生滑动失稳时顶层管袋和斜坡管袋所受水平力、上抬力、抵抗力及倾覆失稳时相应力矩的影响,计算出相应力和力矩的变形因子,进一步完善了考虑管袋变形情况的稳定性公式。该公式充分考虑了管袋变形因素,具有较强的工程实践意义。

[ 1 ] 束一鸣.我国管袋坝工程技术进展[J].水利水电科技进展2018,38(1):1-11.(SHU Yiming.Advances in technology of geotube dam engineering in China[J].Advances in Science and Technology of Water Resources,2018,38(1):1-11. (in Chinese))

[ 2 ] 刘欣欣,束一鸣,尹家春,等.河口海岸扁平管袋裸坝稳定性计算方法研究[J].人民黄河,2016,38(7):114-118.(LIU Xinxin,SHU Yiming,YIN Jiachun,et al.Research on stability calculation method of flat geotube embankment[J].Yellow River,2016,38(7):114-118.(in Chinese))

[ 3 ] RESTALL S J,JACKSON L A,HEERTEN G,et al.Case studies showing the growth and development of geotextile sand containers:an Australian perspective[J].Geotextiles and Geomembranes,2002,20(5):321-342.

[ 4 ] ALVAREZ E,RUBIO R,RICALDE H.Beach restoration with geotextile tubes as submerged breakwaters in Yucatan,Mexico[J].Geotextiles and Geomembranes,2007,25(4):233-241.

[ 5 ] FOWLER J.Geotextile tubes and flood control[J].Geotechnical Fabrics Report,1997,15(5):28-37.

[ 6 ] 陆忠民.土工合成材料在潮汐河口地区水库建设中的应用[J].水利水电科技进展,2009,29(6):39-41.(LU Zhongmin.Application of geosynthetics to reservoir construction in tidal estuary area[J].Advances in Science and Technology of Water Resources,2009,29(6):39-41.(in Chinese))

[ 7 ] 张俊平.土工织物充填袋在黄骅神华港一期工程中的应用[J].中国港湾建设,2002(2):46-48.(ZHANG Junping.Use of stuffed geotextile container in phase one of Shenhua Port in Huanghua[J].Chnia Harbour Engineerinlg,2002(2):46-48.(in Chinese))

[ 8 ] 吴海民,束一鸣,常广品,等. 高含黏(粉)粒土料充填管袋高效脱水技术[J].水利水电科技进展, 2018,38(1):19-27.(WU Haimin,SHU Yiming,CHANG Guangpin,et al.Efficient dewatering technology of geotextile tubes filled with high clay (silt) particle-content soil[J].Advances in Science and Technology of Water Resources,2018,38(1):19-27. (in Chinese)

[ 9 ] RECIO J,OUMERACI H.Effect of deformations on the hydraulic stability of coastal structures made of geotextile sand containers[J].Geotextiles & Geomembranes,2007,25(4/5):278-292.

[10] SHIN E C,OH Y I.Analysis of geotextile tube behaviour by largescale field model tests[J].Geosynthetics International,2003,10(4):134-141.

[11] RECIO J,OUMERACI H.Process based stability formulae for coastal structures made of geotextile sand containers[J].Coastal Engineering,2009,56(5/6):632-658.

[12] 朱朝荣.管袋堤坝施工期稳定性试验研究[D].南京:河海大学,2006.

[13] 易进蓉,黄荣.管袋堤坝波浪作用下波浪压力的数值模拟研究[J].水电能源科学,2014,32(6):97-99.(YI Jinrong,HUANG Rong.Numerical simulation of wave pressure under waves of geo-tube dam[J].Water Resources and Power,2014,32(6):97-99.(in Chinese))

[14] 戴林军,束一鸣,林刚.管袋结构在波浪作用下的稳定尺度试验[J].水利水电科技进展,2011,31(1):56-58.(DAI Linjun,SHU Yiming,LIN Gang.Stability scale test of geotube structure under wave action[J].Advances in Science and Technology of Water Resources,2011,31(1):56-58.(in Chinese))

[15] 满晓磊,束一鸣,曹明杰,等.管袋坝袋间接缝坝芯吹填砂流失模型试验[J].水利水电科技进展,2018,38(1):28-35.(MAN Xiaolei,SHU Yiming,CAO Mingjie,et al.Experimental study on dam core sand scouring through seams between tubes of a geotube dam[J].Advances in Science and Technology of Water Resources,2018,38(1):28-35. (in Chinese))