MASNUM-WAM海浪模式集合Kalman滤波同化研究*——II. 集合样本对同化效果的影响

孙 盟 尹训强, 杨永增,① 吴克俭 孙宝楠

(1. 中国海洋大学海洋与大气学院 青岛 266100; 2. 国家海洋局第一海洋研究所海洋环境与数值模拟研究室青岛 266061; 3. 海洋国家实验室区域海洋动力学与数值模拟功能实验室 青岛 266071)

海浪数据同化是改善海浪模式和提高海浪预报水平的重要途径之一。影响同化效果的关键因素之一是背景误差的确定。背景误差是模拟与真值的偏差。由于真值是未知的, 通常需要对背景误差进行近似构造和估计, 不同的同化方法对此有各自的处理方式。最优插值方法(Lorenc, 1981)将背景误差作为一个常值, 同化过程中仅对其进行一次估计, 即静态统计。集合Kalman滤波方法(Kalman, 1960; Kalman et al,1961; Evensen, 1994; Burgers et al, 1998)是当前较为先进的同化方法, 同化过程中, 多个模式同时运行,模式集合可以对背景误差进行实时更新和动态估计。由此, 集合Kalman滤波(Ensemble Kalman Filter, 简称EnKF)对计算资源的要求较高。基于传统集合滤波方法, Anderson(2001, 2003)提出了集合调整 Kalman滤波(Ensemble Adjustment Kalman Filter, 简称EAKF)。 该方法无需对观测进行扰动,其引入了一个线性算子, 用于替代传统的增益矩阵。当集合数目较小时(10—20个), EAKF方法的表现优于 EnKF(Evensen, 2003)。

在海洋和大气领域, 已有采用EAKF方法的相关研究工作(Zhang et al, 2005; Karspeck et al, 2007;Zhang et al, 2007; Yin et al, 2010, 2011; Karspeck et al,2013; Chen et al, 2016; Hill et al, 2016; Shen et al,2016)。 但具体到海浪资料同化, 相关研究较少。孙盟等(2014)提出基于静态样本的集合 Kalman滤波同化方法, 采用24h间隔有效波高模拟偏差构造误差集合, 用于近似背景误差, 将该误差集合与模式变量相叠加, 构成模式状态变量集合, 结合两步滤波方法得到再分析的波高场, 同化效果显著。静态样本集合Kalman滤波方法仅需运行一个海浪模式, 大大降低了对计算资源的需求, 适用于业务化海浪预报。为了量化该方法与传统集合滤波方法的差异, 本文分别采用静态样本集合Kalman滤波和EAKF方法, 开展海浪资料同化实验。EAKF同化方案需要构造具有代表性的模式集合。 考虑到海浪模式对于初始场的敏感性较弱, 本文对风场进行随机场集合扰动(孙盟等,2016), 由风场集合驱动生成海浪模式集合。

本文基于MASNUM-WAM海浪模式, 针对2014年全球海域, 分别采用静态样本集合 Kalman滤波和EAKF同化方法, 利用Jason-2卫星高度计资料, 开展海浪资料同化实验。上述为引言, 第一节为模式与数据介绍, 第二节为同化方案与实验设计, 其中详细介绍了静态样本集合Kalman滤波同化方案、EAKF同化方案及实验设计, 第三节为实验结果与分析, 最后一节为结论。

1 模式与数据

本文采用球坐标系下的第三代海浪模式MASNUM-WAM(Marine Science and Numerical Modeling) (Yuan et al, 1991, 1992; 杨永增等, 2005)。该模式应用了基于破碎波统计理论发展的海浪破碎耗散源函数(Yuan et al, 1986), 并采用复杂特征线嵌入计算格式。球坐标系下, 波谱能量平衡方程和复杂特征线方程如式(1)和式(2)(3)(4)所示,

其中, 波数谱 E =E（ K ,λ , φ,t）为波数、经度λ和纬度φ的函数;表示背景流场;）表示群速度。等式(1)右侧包含风输入项、破碎耗散项、底摩擦耗散项、非线性波-波相互作用项和波流相互作用项。θ1为波数矢量辐角(指向东为 0, 逆时针旋转为正),）表示波矢量的单位矢量,）表示频散关系。

波数谱被离散成24个方向和25个波数, 对应频率范围是 0.042—0.413Hz。本文模式计算区域为:60°S—60°N; 0°—360°, 空间分辨率为 0.5°×0.5°, 时间步长为 15min, 模式输出为 1h一次。地形数据为ETOPO5。风场数据采用2014年全球ECMWF风场(ERA-Interim), 该数据由欧洲中期天气预报中心提供。风场数据时间间隔为 6h, 空间分辨率为 0.5°×0.5°。

海浪同化资料采用 Jason-2卫星高度计数据。Jason-2为Topex/Poseidon和Jason-1的后继卫星, 于2008年 6月发射升空, 工作至今, 重复周期约为 10天, 测高精度为2.5cm。海浪同化检验资料采用Saral卫星高度计数据。Saral卫星隶属于印度空间研究组织(ISRO), 由法国国家空间研究中心(CNES)研制,其轨道路线沿袭了ERS-1/2和Envisat卫星的轨道设置。该卫星于2013年2月发射升空, 工作至今, 重复周期约为35天, 测高精度为8mm。上述卫星资料由AVISO(Archiving, Validation and Interpolation of Satellite Oceanographic)提供。

2 同化方案与实验设计

本文分别采用静态样本集合 Kalman滤波和EAKF方法, 针对 2014年全球海域开展海浪资料同化实验。静态样本集合Kalman滤波方案介绍详见2.1节; EAKF方案介绍详见2.2节。海浪同化实验设计介绍详见2.3节。

2.1 静态样本集合Kalman滤波方案

静态样本集合Kalman滤波(孙盟等, 2014)同化过程可分为两个部分。首先利用海浪模式历史数据, 由24h间隔有效波高模拟偏差构造误差集合, 如式(5)所示, 该误差集合可用于近似背景误差, 将此误差集合与同化时刻的模式变量相叠加, 构成模式状态变量集合。然后, 采用两步滤波方法对模式状态变量集合进行更新, 生成再分析的波高场。该方法仅需运行一个海浪模式, 可以大幅度降低计算成本, 适用于业务化海浪预报。本文利用2013年12月份海浪模式结果,构造静态样本集合, 已知模式结果输出频率为1h, 故集合样本数目为720个。

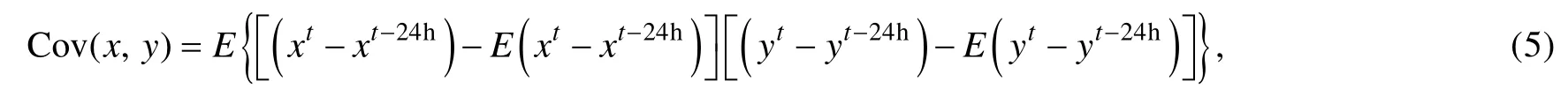
其中, Cov(x,y)表示空间两点x和y的协方差, 上角标t和t–24h表示时间, E表示期望。

2.2 EAKF方案

(1) EAKF方法简介

根据上述定义, 联合向量的概率密度函数可表示为

其中,tkY 表示t时刻以前的所有观测及t时刻的k个观测子集。结合贝叶斯公式, 得到

上式表示, 一个新的观测资料子集合将如何改变基于已有观测资料更新得到的初猜联合向量。

当假设观测资料误差和先验概率密度分布为高斯分布时, 式(8)可视为两个高斯过程的卷积,结果仍为高斯分布, 新高斯过程的协方差矩阵和均值为

其中, R代表观测误差协方差矩阵。引入线性算子A(满足 ∑u= A∑pAT), 用于更新联合向量的每个样本。

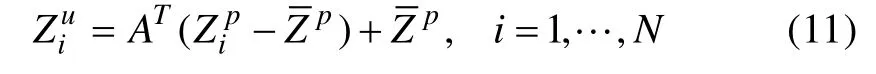
EAKF方法的主要优点在于无需对观测进行样本化处理, 尽可能的保留经验分布中的非线性高阶信息, 此外, 当集合数目相对较小时, 该方法能够获得合理可靠的结果(Anderson, 2001)。

(2) 模式集合的构造

在EAKF方案中, 多个海浪模式同时运行, 该方法的关键是构造具有代表性的海浪模式集合。考虑到海浪模式对于初始场的敏感性较弱, 此处对风场进行持续地集合扰动, 由风场集合驱动生成海浪模式集合。风场集合扰动采用随机场扰动方案(孙盟等,2016), 如式(12)所示, 风场集合由当前时刻风场矢量和扰动集合叠加而成, 扰动集合为三维随机场, 该随机场根据蒙特卡罗方法生成(Evensen, 1994), 其整体满足正态分布, 单个随机场样本的空间分布具有局地性和平滑性。

2.3 实验设计

对 2014 年全球海域(60°S—60°N, 0°—360°)开展海浪集合滤波同化实验, 实验分为三组, 分别为未加入同化的控制实验、静态样本集合Kalman滤波同化实验和 EAKF同化实验(集合数目为 10个)。同化数据为 Jason-2卫星高度计资料, 同化结果检验数据为Saral卫星高度计资料。

海浪同化系统运行流程如图1所示。海浪模式初始化后, 每间隔6h同化一次。同化过程中, 由单个海浪模式(静态样本集合 Kalman滤波方案)或海浪模式集合(EAKF方案)输出控制文件和海浪谱, 调用同化模块, 待控制文件被同化模块删除后, 输入再分析的海浪谱, 海浪模式继续向前积分, 至此完成一次海浪资料同化过程。同化模块启动后, 读入控制文件和海浪谱, 判断同化方法的类型, 若为静态样本集合Kalman滤波方案, 则利用静态样本集合构造模式状态变量集合; 若为EAKF方案, 则直接利用多个模式的变量构造模式状态变量集合。随后同化模块利用两步滤波方法, 对模式状态变量集合进行更新, 输出同化后的海浪谱并删除控制文件。

海浪模式运行过程中对二维海浪谱进行积分计算, 有效波高为海浪谱的积分量。同化过程中, 本文采用 Esteva(1988)的方法对海浪谱进行调整, 即仅对波谱总能量进行比例系数缩放, 不改变谱形, 如式(13)所示。

其中, 上标a和b分别表示同行后和同化前, 下标i和j分别表示经度和纬度方向的空间网格, E(f, θ)表示二维波谱, f和θ分别表示频率和方向, H表示有效波高。

图1 海浪同化系统运行流程Fig.1 Flowchart of wave data assimilation system

3 同化实验结果与分析

利用Saral卫星高度计资料检验海浪数据同化实验结果。由于卫星高度计观测为沿轨数据, 海浪模式输出结果为网格数据, 对实验结果进行误差统计前,本文利用双线性插值方法, 对模拟结果和观测资料进行了时空匹配处理。实验结果检验分为两个部分,整体误差统计和误差时空分布特征分析。

3.1 整体误差统计

为检验同化实验的整体效果, 采用绝均差和均方根误差公式, 对有效波高模拟误差进行分区统计分析。根据通常意义的地理纬度划分标准及风浪和涌浪全球空间分布特征(Chen et al, 2002), 考虑了高纬度地区海冰的季节性变化和卫星高度计的实际观测范围, 划分误差统计分区如图2所示, 统计结果见表1和表 2。从表 1中全球统计结果来看, 与控制实验相比, 两组同化实验的有效波高模拟绝均差和均方根误差减少了约 25%和 20%, 静态样本集合 Kalman滤波方法和EAKF方法的同化效果显著, 两者同化效果相差不大。在统计分区Ⅰ和 Ⅲ , EAKF 方案的有效波高模拟误差明显小于静态样本集合Kalman滤波方案; 在统计分区Ⅱ, 情况相反, 后者表现更佳。

为了检验模拟与观测的线性相关程度, 绘制模拟-观测空间散点图。具体做法为: 将有效波高的模拟-观测空间划分为分辨率 0.05m×0.05m 的网格, 统计落在每个网格内的观测点数目, 统计结果如图 3所示。散点分布越集中于黑色对角虚线, 说明模拟与观测的线性相关程度越高, 与控制实验相比, 两组同化实验的散点分布更集中于对角线。与控制实验相比,静态样本集合Kalman滤波和EAKF方案的模拟-观测相关系数提高了约4.7%和4.9%。

图2 有效波高模拟误差统计分区示意图Fig.2 Schematic diagram of statistical regions for SWH simulation error

表1 2014年有效波高模拟绝均差统计结果Tab. 1 Mean absolute error comparing simulated SWH with observations from satellite Saral

表2 2014年有效波高模拟均方根误差统计结果Tab.2 Root mean square error comparing simulated SWH with observations from satellite Saral

此外, 从图 3中可以看出, 当有效波高较小时(4m 以下), 模拟较观测偏大, 当有效波高较大时(4m以上), 模拟较观测偏小。为了进一步了解两组同化实验对于不同区间内有效波高的修正情况, 将有效波高划分三个区间, 0.5—2m、2—4m和4m以上, 针对上述三个区间, 分别统计模拟误差的概率密度分布,如图4所示。

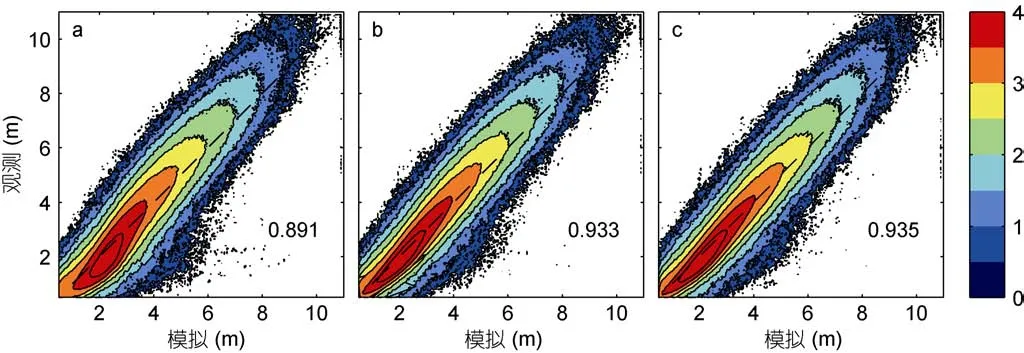
图3 2014年全球有效波高模拟-观测空间散点图Fig.3 Scatter diagrams comparing simulated SWH with global observations in 2014

图4 2014年全球有效波高模拟误差概率密度分布Fig.4 Probability density distribution of global SWH simulation error in 2014

图 4中, 曲线峰值越接近于 0, 说明模拟误差的均值越小, 曲线的聚拢程度表示模拟误差相对于其均值的集中程度。当有效波高观测值在0.5—2m区间内, 模拟较观测偏大, 静态样本集合 Kalman滤波方案对控制实验的改善优于EAKF方案; 当有效波高观测值在2—4m区间内, 模拟与观测相差不大, 两组同化方案对控制实验的改善程度相当; 当有效波高观测值大于4m时, 模拟较观测偏小, EAKF方案对控制实验的修正优于静态样本集合Kalman滤波方案。

通过上述整体统计分析, 可以得到以下结论, 静态样本集合Kalman滤波和EAKF方案同化效果显著,总体来讲, 两者相差不大; 在波高较小的低纬度地区,前者占优; 在波高较大的中高纬度地区, 后者占优。

3.2 误差时空分布特征分析

为进一步检验和评估静态样本集合Kalman滤波和EAKF方案的同化效果, 本节将对有效波高模拟绝均差的空间分布和时间序列进行统计, 分析两组同化实验的误差时空分布特征。

(1) 误差空间分布

为了解两组同化实验的有效波高模拟误差空间分布特征, 分别统计控制实验和两组同化实验的有效波高模拟绝均差空间分布情况。与控制实验相比,静态样本集合Kalman滤波和EAKF同化实验的有效波高模拟绝均差减小量的空间分布如图5所示。从图中可以看出, 两组同化实验效果显著, 且相差不大。静态样本集合具有背景误差的特征信息。静态样本集合采用24h间隔有效波高模拟偏差近似背景误差, 单个时刻仅存在一个误差样本, 为获取足够多的样本,该方法对有效波高历史模拟结果进行长时间序列采样, 由此, 静态样本集合包含了每个空间位置在某时段内的背景误差的特征信息, 这也是静态样本集合Kalman滤波方法的优势之一。

图5 2014年有效波高模拟绝均差同化减小量的空间分布(m)Fig.5 Spatial distribution of MAE reduction of simulated SWH with assimilation in 2014 (unit: m)

此外, 从图5可以看出, 两组同化实验有效波高模拟绝均差减小量的空间分布结构类似, 低纬度地区的同化效果优于中高纬度地区, 这与涌浪和风浪在某空间位置的比例有关。大洋东岸的热带和副热带海域, 存在明显的涌浪区, 特别是太平洋和大西洋,涌浪区显著(Chen et al, 2002)。海浪同化过程中, 对波谱进行了整体缩放。风浪受风强迫的影响, 变化较快,同化信息难以长时间保留; 与之相反, 涌浪则能够较好的保留海浪同化信息, 因此低纬度地区的同化效果优于中高纬度地区。

从有效波高模拟绝均差同化减小量的空间分布情况来看, 静态样本集合Kalman滤波和EAKF同化效果相近, 但仍然存在一定的差异。为更直观地分析两组同化方案效果的差异, 将两者的有效波高模拟绝均差做差, 后者减前者, 得到两者同化效果差异的空间分布, 如图6所示。

图6 2014年静态样本集合Kalman滤波和EAKF有效波高模拟绝均差的差异的空间分布(m)Fig.6 Spatial distribution of difference of MAE of simulated SWH between static sample ensemble Kalman filter and EAKF(2014, units: m)

图 6中, 蓝色代表 EAKF同化方案的优势区域,红色代表静态样本集合Kalman滤波同化方案的优势区域, 白色代表两者同化效果相当的区域。从图中可以看出, 在中高纬度地区, EAKF方案表现较好, 在低纬度地区, 静态样本集合 Kalman滤波方案表现较好, 两者的差异幅度约为 0.02m。EAKF方案具有传统集合滤波方法的天然优势, 包含背景误差的瞬时信息, 在风场变化较大的中高纬度地区, 特别是西风带区域, 其优势显著。在EAKF方案中, 风场扰动对风浪的影响较大, 对涌浪的影响则较小; 在静态样本集合 Kalman滤波方案中, 静态样本的构造方式决定了其能够包含更多的涌浪信息; 由此, 前者的空间相关系数较后者相对局地化, 该情况在涌浪占主导的低纬度地区更加凸显, 这也是后者同化效果在低纬度区域略优于前者的原因。

(2) 误差时间序列

为了解两组同化实验的有效波高模拟误差时间分布特征, 统计控制实验和两组同化实验的有效波高模拟绝均差随时间的变化情况。对每个误差统计分区(如图 2所示), 逐日统计有效波高模拟绝均差,得到模拟误差时间序列如图 7所示。从图 7(b)(c)和(d)蓝色曲线变化情况可以看出, 控制实验在低纬度地区(30°S—30°N)及中高纬度地区(30°N—60°N, 30°S—60°S)的夏季, 有效波高模拟绝均差在0.6m上下浮动, 在其他区域和时段内, 模拟误差位于 0.8m 上下, 即风场变化较小时, 海浪模式的模拟效果更好。从图7(b)(c)和(d)绿色和红色曲线变化情况可以看出, 在风场变化较小的区域和时段内,静态样本集合Kalman滤波和EAKF方案的同化效果显著且两者差异不大; 两者的差异主要体现在中高纬度地区的冬季, 后者具有明显优势。从图 7(a)全球范围内的模拟误差统计结果来看, 两组同化实验的有效波高模拟绝均差变化曲线几乎重合, 基本稳定在0.5m上下。

图7 2014年有效波高模拟绝均差随时间变化曲线(m)Fig.7 Curves of MAE of simulated SWH in 2014 (unit: m)

为更直观地分析静态样本集合 Kalman滤波和EAKF方案同化效果的差异, 在不同统计分区内, 将两者的有效波高模拟绝均差逐日做差, 后者减前者,得到两者差异随时间的变化情况, 如图8所示。

图8 2014年静态样本集合Kalman滤波和EAKF有效波高模拟绝均差的差异随时间变化曲线(m)Fig.8 Curves of difference of MAE of simulated SWH between static sample ensemble Kalman filter and EAKF in 2014 (unit: m)

在图8中, 虚线(零线)以下代表EAKF方案占优,虚线以上代表静态样本集合Kalman滤波方案占优。从全球统计结果(绿色曲线)来看, 两种方案的同化效果相当, 两者差异在零线上下浮动, 幅度约为0.02m。在低纬度地区(30°S—30°N), 静态样本集合Kalman滤波同化方案优势明显, 两者差异在 0.03m上下浮动; 在中高纬度地区(30°N—60°N, 30°S—60°S), 风速较大, 且风场变化较快, EAKF同化方案优势明显。从图中蓝色曲线(30°N—60°N)的变化情况可以看出, 北半球的冬季, 风场变化较大, EAKF方案优势显著; 北半球的夏季, 风场变化相对冬季更为平稳,静态样本集合Kalman滤波方案占优。从图中红色曲线(30°S—60°S)的变化情况, 可以得到上述类似的结论。

4 结论

背景误差是影响海浪同化效果的关键因素之一,最优插值和三维变分方法仅对背景误差进行一次估计, 即“静态”统计, 集合 Kalman滤波方法可以对背景误差进行“动态”统计, 实时更新背景误差, 是更为合理的方法。但集合Kalman滤波方法对计算资源的要求较高, 在实际应用中难以实现。孙盟等(2014)提出基于静态样本的集合 Kalman滤波同化方法, 该方法利用24h有效波高模拟偏差构造静态样本集合, 用于近似背景误差, 在同化时刻, 将静态样本集合叠加到有效波高场, 实现模式状态变量集合的构造, 该方法仅需运行一个海浪模式, 可大大降低对计算资源的需求。为量化静态样本集合Kalman滤波同化方案与传统集合 Kalman滤波同化方案的差异, 本文基于MASNUM-WAM 海浪模式, 采用静态样本集合Kalman滤波和EAKF方法, 利用Jason-2卫星高度计资料, 针对 2014年全球海域开展了海浪资料同化实验。EAKF同化方案需要构造具有代表性的海浪模式集合, 本文采用随机场扰动方案(孙盟等, 2016), 对风场进行集合扰动, 再由风场集合驱动生成海浪模式集合。同化实验的检验资料为Saral卫星高度计资料, 结果表明, 两组同化实验的效果显著, 有效波高模拟绝均差和均方根误差较未加入同化的控制实验减小了约25%和20%。根据2014年全球的误差统计结果, 静态样本集合Kalman滤波和EAKF方案的同化效果相差不大, 但两者仍然存在一定差异。在风场变化较小的低纬度地区,静态样本集合Kalman滤波方案较EAKF方案略优; 在风场变化较大的中高纬度地区, EAKF方案优势显著。

静态样本集合Kalman滤波同化方案在同化过程中, 仅需运行一个海浪模式, 大大降低了计算成本,虽然其在中高纬度地区的表现不如 EAKF同化方案,但从整体统计结果来看, 静态样本集合 Kalman滤波方案的同化效果已经十分接近EAKF同化方案的同化效果, 是一种性价比较高的海浪数据同化方案,可应用于海浪实时业务化预报和历史再分析数据的重构。

孙 盟, 尹训强, 杨永增, 2014. 静态集合样本的构造及其在全球海浪滤波同化中的应用. 海洋与湖沼, 45(5):918—927

孙 盟, 尹训强, 杨永增等, 2016. MASNUM-WAM海浪模式集合Kalman滤波同化研究—I. 风场扰动对海浪模拟影响.海洋与湖沼, 47(6): 1091—1100

杨永增, 乔方利, 赵 伟等, 2005. 球坐标系下 MASNUM 海浪数值模式的建立及其应用. 海洋学报, 27(2): 1—7

Anderson J L, 2001. An ensemble adjustment Kalman filter for data assimilation. Monthly Weather Review, 129(12):2884—2903

Anderson J L, 2003. A local least squares framework for ensemble filtering. Monthly Weather Review, 131(4): 634—642

Burgers G, Jan van Leeuwen P, Evensen G, 1998. Analysis scheme in the ensemble Kalman filter. Monthly Weather Review, 126(6): 1719—1724

Chen G, Chapron B, Ezraty R et al, 2002. A global view of swell and wind sea climate in the ocean by satellite altimeter and scatterometer. Journal of Atmospheric and Oceanic Technology, 19(11): 1849—1859

Chen H, Yin X Q, Bao Y et al, 2016. Ocean satellite data assimilation experiments in FIO—ESM using ensemble adjustment Kalman filter. Science China Earth Sciences,59(3): 484—494

Esteva D C, 1988. Evaluation of preliminary experiments assimilating Seasat significant wave heights into a spectral wave model. Journal of Geophysical Research, 93(C11):14099—14105

Evensen G, 1994. Sequential data assimilation with a nonlinear quasi—geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research:Oceans, 99(C5): 10143—10162

Evensen G, 2003. The Ensemble Kalman Filter: theoretical formulation and practical implementation. Ocean Dynamics,53(4): 343—367

Hill A J, Weiss C C, Ancell B C, 2016. Ensemble sensitivity

analysis for mesoscale forecasts of dryline convection initiation. Monthly Weather Review, 144(11): 4161—4182 Kalman R E, 1960. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 82(1):35—45

Kalman R E, Bucy R S, 1961. New results in linear filtering and prediction theory. Journal of Basic Engineering, 83(1):95—108

Karspeck A R, Anderson J L, 2007. Experimental implementation of an ensemble adjustment filter for an intermediate ENSO model. Journal of Climate, 20(18): 4638—4658

Karspeck A R, Yeager S, Danabasoglu G et al, 2013. An ensemble adjustment Kalman filter for the CCSM4 ocean component. Journal of Climate, 26(19): 7392—7413

Lorenc A C, 1981. A global three-dimensional multivariate statistical interpolation scheme. Monthly Weather Review,109(4): 701—721

Shen Z Q, Zhang X M, Tang Y M, 2016. Comparison and combination of EAKF and SIR-PF in the Bayesian filter framework. Acta Oceanologica Sinica, 35(3): 69—78

Yin X Q, Qiao F L, Shu Q, 2011. Using ensemble adjustment Kalman filter to assimilate Argo profiles in a global OGCM.Ocean Dynamics, 61(7): 1017—1031

Yin X Q, Qiao F L, Yang Y Z et al, 2010. An ensemble adjustment Kalman filter study for Argo data. Chinese Journal of Oceanology and Limnology, 28(3): 626—635

Yuan Y L, Hua F, Pan Z D et al, 1991. LAGFD-WAM numerical wave model——I. basic physical model. Acta Oceanologica Sinica, 10(4): 483—488

Yuan Y L, Hua F, Pan Z D et al, 1992. LAGFD-WAM numerical wave model—Ⅱ. Characteristics inlaid scheme and its application. Acta Oceanologica Sinica, 11(1): 13—23

Yuan Y L, Tung C C, Huang N E, 1986. Statistical characteristics of breaking waves. In: Phillips O M, Hasselmann K eds.Wave Dynamics and Radio Probing of the Ocean Surface.New York: Springer, 265—272

Zhang S, Harrison M J, Rosati A et al, 2007. System design and evaluation of coupled ensemble data assimilation for global oceanic climate studies. Monthly Weather Review, 135(10):3541—3564

Zhang S, Harrison M J, Wittenberg A T et al, 2005. Initialization of an ENSO forecast system using a parallelized ensemble filter. Monthly Weather Review, 133(11): 3176—3201